Model Reference Adaptive Control for Switched Systems with Closed-loop Reference Model Under Arbitrary Switching
2019-07-25HaoYangJingXieandJunZhao
Hao Yang,Jing Xie and Jun Zhao
(State Key Laboratory of Synthetical Automation for Process Industries,College of Information Science and Engineering,Northeastern University,Shenyang 110819,China)
Abstract:This paper explores the model reference adaptive control problem for a class of switched linear systems under arbitrary switching with no need for the measurability of the system state.Based on the state of reference model and the measurable output error,adaptive laws and controllers are designed for switched systems.Each subsystem may have its individual reference model and controller,which increases the design flexibility.The introduction of the closed-loop reference model is to get a better transient performance of the whole switched systems.A numerical example is provided to verify the effectiveness of the main results.
Keywords:switched systems;model reference adaptive control;common Lyapunov function;arbitrary switching;the closed-loop reference model
1 Introduction
Switched systems,an important class of hybrid systems,are often encountered in many practical situations.Normally,the switched system is defined as dynamical system which is comprised by series of continuous-time or discrete-time subsystems and a logical rule that decides the switching mechanism among the individual subsystems[1].In the past two decades,more and more researchers and experts have been drawn by switched systems because of a number of applications and the theoretical importance.It is well known that the stability problem is one of key issues of studying switched systems.In order to study the stability of switched systems,some approaches have been proposed; forexample,thecommon Lyapunov function method,dwell time or average dwelltime method,multiple Lyapunov function method[2-15].Among them,the common Lyapunov function method is a particular method which only finds acommon Lyapunov function thatensures stability of the whole switched systems and switching signals is arbitrary[2-4].This method is usually used when we cannot know the switching signal or it is too complex to apply directly in studying the stability problem.
In the real world,many control systems often company with uncertainties including parametric,structural and environmental uncertainties[9,12].Such uncertainties often appear in aircraft engine,mechanical systems,chemical engineering and so on.The existence of uncertainties makes the study of system stability more complicated.As is well known,adaptive control is a powerful tool todeal with uncertainties,which provides adaptive control laws to real-time adjust controllers or system parameters for obtaining desired system performance[16].From a perspective of practicality,the adaptive control can be classified into three types:model reference adaptive control(MRAC),self-tuning controland other adaptive control[17].Amongthem, MRAC is an extensively used method and hasbeen matured theoretically[18-22].The purpose of MRAC is to make the state(or output)of the controlled system track the state(or output)of a preset reference model by designing the controller and adaptive law.In the last decades,there are many results in this field for nonswitched systems[18-22].
However,few results on MRAC for switched systems with parametric uncertainties have been reported so far.Chiang and Fu[23]studied a class of signal-input-signal-output switched systems by means of a variable structure MRAC method,while the requirement limits the design flexibility which the reference model is common for all subsystems.When the state of the system is fully measurable,Liu and Xiang[24]solved the exponential H!output tracking control problem for a class of uncertain switched neutral systems.They presented a concurrent learning model reference adaptive control architecture for this switched systems and the problem of closed loop parameter estimation was solved in the paper[25].Based on the minimal control synthesis algorithm,Bernardo, Montanaro and Santini[26]presented a genericMRAC scheme so thatthe state ofa multimodal piecewise affine system can track asymptotically a given multimodal piecewise affine(or smooth)reference model.But,what needs to point out is that all the above results require the state of controlled system being measurable while it is not reasonable for many practical systems.Therefore,how to deal with the MRAC problem for switched systems which have parametric uncertainties is a practical problem when the state of the system is immeasurable,which is a motivation for this paper.
On the other hand,as we all know,what restricts theapplication ofMRAC isthe poortransient performance.So it must do something to improve MRAC.Recently,several researchers proposed a new class of closed-loop reference model in which the reference model has an observer-like feedback term containing the state error and a feedback gain[18-22].Because of the introduction of the feedback term,the transient performance can be improved by adjusting the feedback gain.In the paper,Gibson,Annaswamy and Lavertsky[18]analyzed how the closed-loop reference model improved the transient performance of MRAC and compared the transient performance of the closed-loop reference model adaptive control system with the classical open-loop reference model control system.Lately,Zheng[22]studied the MRAC state tracking problem with the closed-loop reference model when the state is not available for measurement.However,only non-switched systems are studied.A natural problem arises:how to improve the transient performance of switched systems.Clearly,this is a challenge problem for the switched systems.This is another motivation for this paper.
ThispaperstudiestheMRAC problem for switched systems with parametric uncertainties under arbitrary switching while it is not required the state of the controlled system should be fully measurable.In this paper,the contributions are as follows:first of all,we only use the output and the state of the given closed-loop reference model to design controllers and adaptive laws because the requirementthatthe controlled system state is fully measurable for is hard to achieve in many practical systems.Secondly,all reference models and controllers for subsystems are not common which remarkably add the flexibility of designing.Finally,the introduction of the closed-loop reference model can improve the transient performance of the switched system.
The organization of this paper is as follows.Section 2 gives the problem statement and preliminaries.The design of controllers and adaptive laws and the stability theorem of switched error system are in Section 3.A numerical Simulink example is established to prove the correctness of this theory in Section 4.Section 5 is the conclusion.
Notation:The standard Euclidean or the induced matrix two-norm is denoted as‖·‖.The positivedefinite matrix is P > 0.A-1represents the inverse of a matrix A and ATrepresents the transpose of a matrix A.The smallest eigenvalue of matrix A is defined as λmin(A)and the trace of square matrix A is defined as tr(A).We use I and 0 to denote identity matrix and zero matrix in a block matrix respectively.
2 System Statement and Preliminaries
The switched system with parametric uncertainties in this paper can be described as:
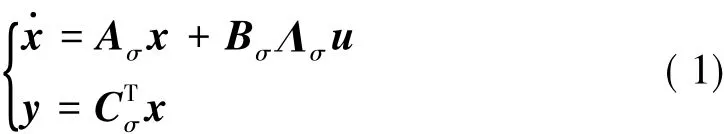
where x∈ Rnis the plant vector,the control input is denoted as u∈Rm,y∈Rmdenotes the plant output.σ(t):[0,+!) →I={1,2,…,N}denotes switching signal of this switched systems and the quantity of the subsystems is N .Bi∈ Rn×mand Ci∈ Rn×mare known constant matrices while Ai∈ Rn×nand Λi∈ Rm×mare unknown,and only y is measurable.
The closed-loop switched reference model is:where r∈Rmis the input signal of reference model and Li∈Rn×mare feedback gains that will be designed suitably.e=x - xmdenotes the state error.There is one-to-one correspondence between the subsystems of the reference model and the controlled system.In this paper,the control objective is to design a switched controller and switched adaptive laws so that the state error converges to 0 i.e.,the state of controlled system x tracks the state of given closed-loop reference model xm.
Remark 1In the classical switched MRAC control problem[23-27],the switched reference model is open-loop switched reference model and the form is given by:

Compared with the open-loop reference model,the closed-loop reference model has an additional feedback term.When we choose Li=0,i∈M or the state errorclosed-loop switched reference model in Eq.(2)degenerates into the open reference switched reference model.Besides, the introduction of the feedback Lican improve the transient performance due to the additional degree of freedom for each subsystem[18-22].
The following assumptions are requisite to achieve the control objective.
Assumption 1The productis full rank,i∈I.
Assumption 2The paiis observable,i∈I.
Assumption 3The subsystems in controlled system(1)are minimum phase.
Assumption 4There existsand Ki*∈Rm×msuch thatI,i∈ I,respectively.
Assumption 5Λiis diagonal with positive elements,i∈ I.
Assumption 6The unknown controlinput matrices Λiand the uncertain matching parametershave priori known upper bounds and the following hold:


Remark 2Assumption 1 actually isthe requirement that Miis nonsingular.Assumption 2 is needed since the feedback gains of the reference model Liare required to use in the following result.Assumption 3 makes the condition of the KYP lemma hold.Assumption 4 is the matching conditions and is commonly used in MRAC[17].Assumption 5 is about the uncertainties and it is routinely satisfied in the area of aerospace industry in which control directions are generally known but we do not know their magnitudes[27].Assumption 6 is for a suitable choice of Li(i∈M).
Lemma 1[21,28]For each subsystem of the switched system(1)satisfying Assumptions 1-3,and Michoose as in Eq.(8).There always exists Lsisuch thatiare strict positive realness(SPR).
Lemma 2[21,29]Tiare chosen and ρi> 0 are arbitrary,then the transfer functionsare SPR and the following hold:
3 Stability Analysis
For the switched system in Eqs.(1)and(2)satisfying the all above assumptions,we design the following switched adaptive controller and adaptive laws:


Remark 3In general,it is hard to measure all the state of the controlled systems in many practical systems.Therefore,we choose the state of the given reference model instead of the controlled system to design the control input Eq.(5).
From Eqs.(1),(2)and(5),we can easily get the following expression of the state error

In the following,we give a sufficient condition under which the MRAC problem is solved.
Theorem 1If there exist P=PT>0 and Q=QT> 0,such that the following holds:
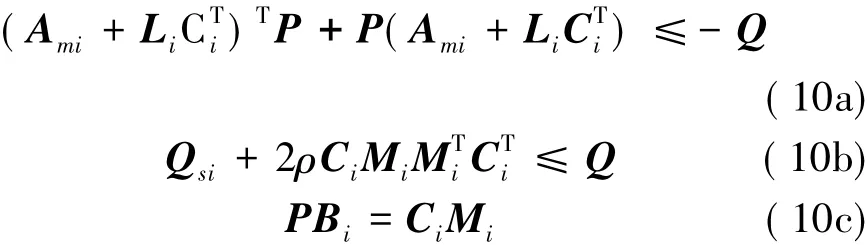
The MRAC problem of switched adaptive system described by Eqs.(1),(2),(5),(6)satisfying Assumptions 1-6 with Lidefined in Eq.(4),Mistated in Eq.(8),ρ> ρ*is solved withare defined in Eq.(3),is defined in=0,where Lemma 2 and

ProofThe Lyapunov function we choose is:

Differentiating V along the active subsystem trajectories in Eq.(9)gives:

According to the property of the matrix trace,we have:
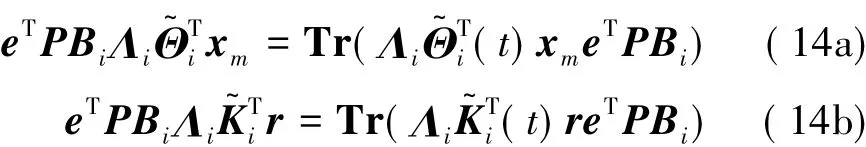
By Eqs.(8),(10)and(14),Eq.(13)can be written as:

By the fact that ey=,we can get=-εT(Q(ρ))ε ,where

Due to ρ> ρ*> 0 and Eq.(11),we have

According to the Schur complement Lemma,Q(ρ)is a positive-definite matrix.Thus< 0,so e,
y.From Eqs.(2)and(9),it can be gotten that.Furthermore,e∈L2because of the positive definiteness of matrix Q(ρ).So we have.By Barbalat Lemma,it followswe can get the boundedness of x.
4 Numerical Examples
In this section,we provide a numerical example to prove the effectiveness of the theorem in this paper.
Considering the switched system(1)and the switched closed-loop reference model(2),the system matrices and parameters are given by:

The plant parameters of the closed-loop reference model are:

The reference input is r(t)=4sin(0.2πt) .From Assumption 4,we have

The parameters of the adaptive laws in Eqs.(6)and(7)are designed as
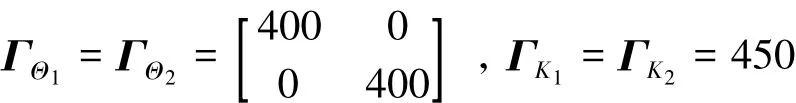
A direct calculation gives
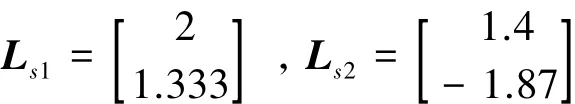
Then,we choose ρ=1.The feedback gains of the reference model are
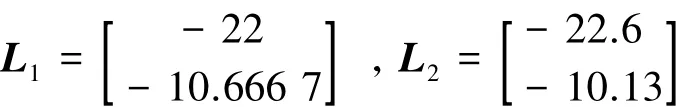
so we have

From Figs.1 - 5,it can be concluded that the switched MRAC problem in Eqs.(1),(2)and(9)with the closed-loop reference model is solved under the adaptive controller(5).Fig.1 is the switching signal.Fig.2 shows that the trajectories of the closedloop reference model are bounded.It shows us that the adaptive parameters of the error systems are bounded from Figs.3-4.From Fig.5,we can get the fact that the state error converges to 0 which implies the state of controlled system can track the state of given switched reference model.

Fig.1 The switching signal
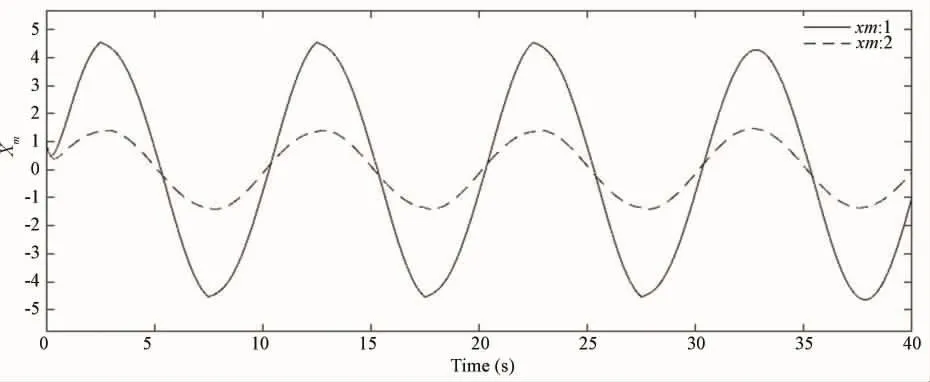
Fig.2 Trajectories of the reference model

Fig.3 Trajectories of adaptive parameters for the control system

Fig.4 Trajectories of adaptive parameters for the reference model

Fig.5 The state error
5 Conclusions
The MRAC problem for the switched systems with parametric uncertainties which has closed-loop reference model for each subsystem under arbitrary switching signals has been solved in this paper.Firstly,the reference model and the controller were not common for all subsystems.Secondly,to get a better transient performance of the whole switched system,the closed-loop reference model has been introduced.Finally,it is hard to measure all of the state of system in many piratical systems,so the design of control input is depended on the state of closed-loop reference modeland the measurable output error in this paper.By appropriate design of the adaptive control laws and the gain of the closed-loop reference models for switched systems,the state tracking errors converged to 0.
杂志排行
Journal of Harbin Institute of Technology(New Series)的其它文章
- High-Resolution ISAR Imaging Based on Sparse Iterative Covariance-Based Estimation
- X-ray Computed Tomography Characterization of 3D Tufted Twill Textile Composite for Aerostructures
- Measurement Uncertainty of Blade Surface by Coordinates Measuring Machines in Rotation and Parallel Sampling Modes
- Exponential Stabilization of Euler-Bernoulli Beam with Input Time-Delay in the Boundary Control
- Support Vector Regression for Bus Travel Time Prediction Using Wavelet Transform
- Tracking Algorithm Based on Improved Interacting Multiple Model Particle Filter
