基于分形理论的驻波声场中颗粒团运动特性数值预测∗
2019-07-25贾文龙凡凤仙苏明旭
贾文龙 凡凤仙 苏明旭
(上海理工大学能源与动力工程学院 上海 200093)
0 引言
悬浮在大气中空气动力学直径小于或等于2.5µm的颗粒物被称为PM2.5,其极易富集重金属和多环芳烃等强致癌污染物,且能够经呼吸系统进入人体,对人群健康带来严重危害;同时,PM2.5影响大气环境,加剧酸雨、光化学烟雾以及雾霾的形成,威胁到人类赖以生存的环境[1−2]。文献报道显示,燃煤电站、交通车辆、工业过程的排放是PM2.5的主要来源[3−5]。由于PM2.5粒径细微,传统的除尘方式,如惯性除尘、湿式除尘、过滤式除尘、静电除尘等对PM2.5的清除均难以奏效,使得大量PM2.5排放到大气中。随着环境空气质量标准的日趋严格,PM2.5排放控制技术研究显得尤为重要且迫切。为了控制PM2.5的排放,一些学者提出了PM2.5凝并预处理技术,以期通过物理或化学作用促进PM2.5长大为粒径较大的颗粒,从而提高传统除尘装置的效率。声凝并是一种重要的PM2.5预处理技术,其原理是利用外加声场作用促进PM2.5发生相对运动、碰撞接触进而凝并为粒径较大的颗粒物[6−7]。该项技术因装置简单、适应性强,而备受研究者关注[8−11]。
为探讨声凝并的内在机理和动力学过程,一些学者对声场中单颗粒的运动[12−13]、颗粒间相互作用[14−17]、颗粒碰撞[18]和凝并[9,19−23]开展了一系列理论和数值模拟研究。然而,这些研究主要针对球形颗粒,甚至在对声凝并进行建模时将固体颗粒声凝并后生成的颗粒团也视为球形[9,20,22−23]。事实上,声凝并形成的颗粒团普遍具有分形结构[19,21,23−24]。虽然研究者利用分形维数描述颗粒团形状[19,21],并将分形维数引入颗粒凝并核函数以建立声凝并模型,模拟声凝并过程中颗粒粒径分布的演变,但模型中未能反映出颗粒团分形结构对其运动特性的影响。赵兵等[24]对颗粒团在驻波声场中的运动轨迹进行可视化实验并对颗粒团弛豫时间进行理论分析,但缺少对声场中颗粒团运动规律的深入探究。杨旭峰等[25]虽然对颗粒团在声场中的动力学特性进行过探讨,但所针对的是直链颗粒团。在声凝并的实际应用中,一旦颗粒凝并形成颗粒团,颗粒团的运动特性将对声凝并过程起决定作用。因此,欲全面掌握声凝并过程中颗粒动力学行为的细节信息,很有必要对声场中颗粒团的运动特性进行研究。
本文将基于分形理论,利用颗粒团的质量-半径关系式和无量纲流体动力学半径-分形维数关系式,求解颗粒团的流体动力学半径和分形维数,进而建立驻波声场中颗粒团动力学模型,并将数值模拟结果与文献中的实验结果进行对比,验证模型的准确性。在此基础上,利用数值模拟方法,预测组成颗粒团的原生颗粒半径、数目和排列情况对颗粒团在声场中运动特性的影响,以揭示颗粒团的行为规律,并为建立更精确的声凝并模型提供理论基础。
1 数学模型与数值计算方法
1.1 分形理论对颗粒团的描述
图1为球形颗粒组成的颗粒团的结构及特征参数示意图,图中ai为组成颗粒团的第i个原生颗粒的半径,R为颗粒团半径,即能够包含颗粒团的最小球体的半径;Rh为颗粒团的流体动力学半径,即与颗粒团质量和动力学特性相同的非渗透性球形颗粒的半径。

图1 颗粒团结构及特征参数示意图Fig.1 Schematic diagram of agglomerate structure and characteristic parameters
组成颗粒团的原生颗粒数目N、原生颗粒半径a与颗粒团的流体动力学半径Rh的函数关系可由质量-半径关系式给出[26−27]:

式(1)中,Df为颗粒团的分形维数,表示颗粒团的空间填充致密程度,取值范围为1 当原生颗粒半径不相等时,式(1)中的原生颗粒半径a可采用体积平均半径aave代替,即 式(2)中,Vt是组成颗粒团的原生颗粒的总体积, 颗粒团的流体动力学半径Rh与颗粒团半径R的比值可写成分形维数Df的函数[27−28],即 联立式(1)、式(4),通过逐次逼近的迭代算法,即可获得颗粒团的流体动力学半径和分形维数。已有研究表明,颗粒团的质量-半径关系式和无量纲流体动力学半径-分形维数关系式,适用于描述原生颗粒数目为2∼100的颗粒团[28−30]。 将水平方向设为x向,由Navier-Stokes方程可推导出一维水平平面驻波声场的波动方程为 式(5)中,u为声波引起的气体振动速度;u为速度振幅;k为波数,k=ω/c,c为声速,ω=2πf,f为声波频率;x为声波波动方向位置坐标;t为时间。 通常采用声压级来描述声场的强度,声压级的表达式为 式(6)中,L为声压级;ρg为气体密度;Pr为参考声压,Pr=2×10−5Pa。 为着重探讨水平驻波声场中单个颗粒团的动力学特性,忽略颗粒团的破碎和重组。声场中颗粒团所受作用力包括重力、浮力、Stokes力和非稳定力(Basset力、虚拟质量力、压力梯度力等),对于气相中的固体颗粒,与Stokes力相比,非稳定力可以忽略不计[13]。因此,若将重力方向设为y向,颗粒团的运动方程可写为 其中,m为颗粒团质量,m=ρVt;ρ为颗粒材料密度;v为颗粒团速度,下标x、y表示在x向和y向的分量;µg为气体动力黏度;g为重力加速度;Cc为Cunningham修正系数,其表达式为[9,18] 式(9)中,Kn为Knudsen数,Kn=λg/Rh,λg为气体分子平均自由程。 依据式(7)、式(8)给出的颗粒团运动方程,采用四阶变步长Runge-Kutta算法计算出经历一个时间步长后颗粒团的速度。在一个时间步长的初速度和末速度已知的前提下,采用二阶隐式Adams插值算法求解颗粒团的位移,即 其中,X和Y分别为颗粒团的x向和y向位移;∆t为时间步长。∆t通常要比声波周期T=1/f和颗粒团弛豫时间τ小得多,其中弛豫时间τ可写为 赵兵等[24]曾采用高速显微摄像系统对水平驻波声场中单个颗粒团的运动轨迹进行可视化实验。图2给出了赵兵等[24]的实验及本文数值模拟所得到的颗粒团运动轨迹。图2(b)给出的数值模拟结果中颗粒团的尺寸采用流体动力学直径(2Rh)表示。数值模拟采用的参数条件与实验一致,具体数值见表1。其中,T为气体温度,p为气体静压,x0为颗粒初始位置。根据颗粒团的组成和结构参数(a、N、Df),利用式(1)计算得到颗粒团的流体动力学半径Rh=2.17µm,据此计算颗粒团的运动。结果显示,数值模拟得到的颗粒团运动轨迹与实验数据吻合良好,都反映出由于水平方向声波对颗粒的黏性夹带作用,颗粒团的运动轨迹呈现出“S”形;驻波声场作用使得颗粒团在水平方向发生往复振动的同时,振动中心向波节点漂移,这种定向漂移效应是由驻波声场中气体介质的非对称运动引起的[9,18,31]。这表明本文的数学模型和计算方法能够合理预测颗粒团在驻波声场作用下的运动特性。 表1 数值模拟参数Table 1 The numerical simulation parameters 图2 实验与数值模拟得到的颗粒团运动轨迹的对比Fig.2 Comparison of the motion trajectories of particle agglomerate obtained by experiment and numerical simulation 由式(1)、式(2)可知,颗粒团的分形维数和流体动力学半径由组成颗粒团的原生颗粒半径、数目和排列情况所决定,而流体动力学半径直接影响到颗粒团的动力学特性。鉴于驻波声场中的颗粒团在声波波动方向上存在边振动、边漂移的运动特性,同时由于惯性颗粒团的振动相位滞后于声波引起的气体介质振动相位,下文利用夹带系数和相位滞后表示颗粒团的振动特性,利用漂移系数表示颗粒团的漂移特性。其中,夹带系数定义为颗粒团速度振幅与颗粒团振动中心位置气体介质速度振幅之比,相位滞后定义为颗粒团振动相位滞后于气体介质的量,漂移系数定义为颗粒团振动中心的漂移速度与颗粒团振动中心位置气体介质速度振幅之比。本部分数值模拟采用的气相温度T、气相静压p、颗粒材料密度ρ、时间步长∆t同表1一致,采用的声场为L=150 dB、f=2000 Hz的驻波声场,颗粒初始位置为x0=7λ/8。 2.2.1 原生颗粒半径对颗粒团运动特性的影响 图3 原生颗粒半径对颗粒团运动特性的影响Fig.3 effect of the radius of primary particles on the motion characteristics of particle agglomerate 图3给出了由半径为a1和a2的两个原生颗粒组成的颗粒团的夹带系数、相位滞后和漂移系数,及与等体积球形颗粒的对比关系。等体积球形颗粒的半径为图中颗粒团及相应的等体积球形颗粒的曲线颜色相同。可见,当a1<0.1µm或a1>5µm时,颗粒团与等体积球形颗粒的夹带系数、相位滞后和漂移系数的差异很小;当0.1µm 6a16 5µm时,颗粒团的夹带系数低于等体积球形颗粒,相位滞后高于等体积球形颗粒;a2较小时,颗粒团的漂移系数低于等体积球形颗粒,a2较大时,颗粒团的漂移系数大于等体积球形颗粒。这是因为当a1<0.1µm或a1>5µm 时,两原生颗粒的半径相差较大,颗粒团的运动特性由粒径较大的原生颗粒决定;同时,等体积球形颗粒的半径也由较大的原生颗粒所主导,使得颗粒团的运动特性与等体积球形颗粒差异很小。然而,当两原生颗粒的半径相差不多时,颗粒团和等体积球形颗粒运动特性的差异变得明显,此时,若将颗粒团当作球形颗粒进行处理,将带来较大的计算误差。 由图3还可以看出,当原生颗粒2的半径a2为0.25µm、0.5µm和1µm时,随着原生颗粒1的半径a1的增加,颗粒团的漂移系数先增加后减小,存在一个漂移系数峰值;当a2=2.5µm时,随着a1的增加,颗粒团的漂移系数趋于减小,这是由颗粒团的惯性决定的。当a2较小(a2<1µm)时,a1由0.01µm增加至10µm的过程中,颗粒团的质量增加,颗粒团由零惯性颗粒向有限惯性颗粒转变[32];颗粒团处于零惯性区域时,其能够被声波充分夹带,运动特性表现为随声波往复振动,此时夹带系数接近1,相位滞后接近0,漂移系数接近0;随着惯性增加,颗粒团处于有限惯性区域,夹带系数单调减小,相位滞后单调增加,起初颗粒运动过程中经历的流场非对称性增强,颗粒团漂移系数增加,但是当颗粒团惯性增加到一定程度时,颗粒团将难以被声波夹带,特别是在极限情况下颗粒团既不发生振动又不发生漂移,漂移系数为0,因此存在一个漂移系数峰值。然而,当a2较大(如a2=2.5µm)时,颗粒团惯性始终保持在较高的水平,颗粒团漂移系数由0增大的阶段将不再存在,因此颗粒团漂移系数呈现出单调减小的特征。 2.2.2 原生颗粒数目对颗粒团运动特性的影响 为了探究原生颗粒数目对驻波声场中颗粒团运动特性的影响,在颗粒团分形维数Df=1.85、原生颗粒半径a=0.25µm条件下,对原生颗粒数目N=2∼100时颗粒团的运动特性进行数值模拟,得到了颗粒团及其等体积球形颗粒的夹带系数、相位滞后和漂移系数随原生颗粒数目的变化关系,如图4所示。结果表明,随着原生颗粒数目的增加,颗粒团的惯性趋于增大,导致其夹带系数减小,相位滞后增加,漂移系数先增大后减小。此外,当原生颗粒数目较少时,颗粒团及相应的等体积球形颗粒的质量均较小,二者都接近于零惯性区域,对声波有很强的跟随性,颗粒团与等体积球形颗粒的运动特性差异较小;但随着原生颗粒数目的增加,颗粒团及等体积球形颗粒惯性增加,由于颗粒团流体动力学半径和等体积球形颗粒半径的差异带来的运动特性的差异变得显著。需要指出的是,图4(c)中,颗粒团和等体积球形颗粒的漂移系数曲线存在一个交点,交点对应的原生颗粒数目为72,这表明此时颗粒团和等体积球形颗粒漂移系数相等。究其原因是,漂移系数随流体动力学半径的增加先增加后减小[31],由于非球形颗粒团的流体动力学半径大于等体积球形颗粒的流体动力学半径,等体积球形颗粒漂移系数的变化滞后于非球形颗粒团,进而引起颗粒团和等体积球形颗粒的漂移系数曲线相交。图4中结果还表明,在声凝并过程中,随着声波作用时间的延长,形成了更多颗粒团,并且颗粒团的粒度也更大,考虑到颗粒团和等体积球形颗粒在运动特性上的显著差异,在对声凝并进行建模时若将颗粒团视为球形,将带来较大的误差,因此有必要在声凝并模型中充分考虑颗粒团的分形结构对其动力学行为的影响。 图4 原生颗粒数目对颗粒团运动特性的影响Fig.4 effect of the number of primary particles on the motion characteristics of particle agglomerate 2.2.3 原生颗粒排列情况对颗粒团运动特性的影响 分形维数Df的大小直接反映了颗粒团中原生颗粒排列的致密程度。Df越小,原生颗粒排列越松散;Df越大,原生颗粒排列越致密。为了探讨原生颗粒排列情况对颗粒团运动特性的影响,对由5个相同半径的原生颗粒组成的颗粒团在驻波声场中的运动特性进行数值预测。图5给出了颗粒团中原生颗粒的排列示意图。图中,θ为旋转角,即以直链形颗粒团为基准,右边3个颗粒绕基准颗粒团的质心旋转,与基准位置的夹角。对于图5所示的颗粒团结构,在原生颗粒半径a和旋转角θ给定的条件下,根据几何关系确定颗粒团的半径R,联立式(1)、式(4),求解获得颗粒团的分形维数Df和流体动力学半径Rh。 图5 颗粒团中原生颗粒排列情况示意图Fig.5 Schematic diagram of the packing structure of primary particles in particle agglomerate 图6给出了数值模拟得到的颗粒团的夹带系数、相位滞后和漂移系数随分形维数的变化关系。在θ由0◦增加至120◦的过程中,原生颗粒的排列变得更加致密,颗粒团的分形维数增加,由式(1)可见颗粒团的流体动力学半径减小,颗粒团更容易被声波夹带,导致夹带系数增加,同时相位滞后减小。由于等体积球形颗粒可视为原生颗粒的最致密排列形成的颗粒团(对应于Df=3),等体积球形颗粒的运动特性不随颗粒团分形维数的变化而变化,且其夹带系数比实际颗粒团高,而相位滞后比实际颗粒团低,等体积球形颗粒与线形颗粒团振动特性差异最大。图6的结果还表明,颗粒团与等体积球颗粒漂移系数的差异随分形维数的增加而减小,这是因为分形维数越大,颗粒团的结构越致密,颗粒团流体动力学半径与等体积球颗粒粒径差异越小,导致漂移速度差异缩小。此外,在原生颗粒粒径较小时(a6 0.5µm时),漂移系数随分形维数的增加而减小;在原生颗粒粒径较大时(a>1.0µm时),漂移系数随分形维数的增加而增大。其原因是原生颗粒粒径的增加导致颗粒团的流体动力学半径增加,当颗粒团的流体动力半径达到一定值时,颗粒团的定向漂移运动受到抑制。 图6 原生颗粒排列情况对颗粒团运动特性的影响Fig.6 effect of the packing structure of primary particles on the motion characteristics of particle agglomerate 基于分形理论的质量-半径关系式和颗粒团无量纲流体动力学半径分形维数关系式,建立外加声场作用下球形原生颗粒组成的颗粒团的动力学模型,利用四阶变步长Runge-Kutta算法和二阶Adams插值算法对颗粒团运动方程进行求解,将模拟结果与实验结果进行对比,验证了数值模拟结果的正确性。在此基础上,对颗粒团在驻波声场中的夹带系数、相位滞后和漂移系数随原生颗粒半径、数目和排列情况的变化特性进行数值预测,并与等体积球形颗粒进行比较。通过本文研究,得出以下结论: (1)对于两个原生颗粒组成的颗粒团,两个原生颗粒的半径相差较大,颗粒团与等体积球形颗粒的运动特性差异很小;当两原生颗粒的半径相差不多时,颗粒团和等体积球形颗粒运动特性的差异变得明显。 (2)分形维数一定时,随着原生颗粒数目的增多,颗粒团的夹带系数减小,相位滞后增加,漂移系数先增大后减小,颗粒团与等体积球形颗粒的动力学行为存在显著差异。 (3)原生颗粒的排列情况决定了颗粒团的分形维数,原生颗粒的排列趋于致密时,分形维数增加,引起颗粒团的夹带系数增加,相位滞后减小,漂移系数发生单调变化,颗粒团与等体积球形颗粒的运动特性的差异趋于减小。
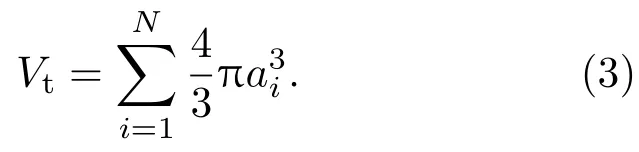

1.2 声波的波动方程


1.3 颗粒团的动力学模型
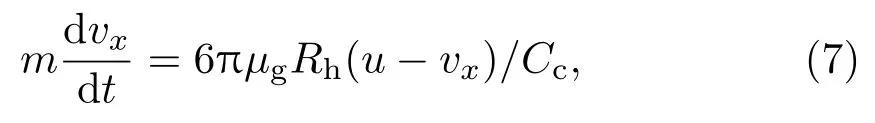

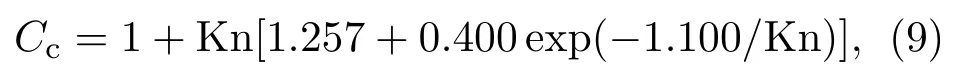
1.4 数值计算方法


2 数值模拟结果
2.1 模型验证


2.2 颗粒团的运动特性




3 结论
