水工波纹管伸缩节位移补偿极限能力研究

石长征，伍鹤皋，刘 园，2，李 云，朱国金

(1.武汉大学水资源与水电工程科学国家重点实验室，湖北武汉430072；2.中国电建集团中南勘测设计研究院有限公司，湖南长沙410014；3.中国电建集团昆明勘测设计研究院有限公司，云南昆明650000)

伸缩节是压力钢管中为减少或消除由温度变位或不均匀地基变形所产生的附加应力而设在两镇墩或厂坝之间的构件。波纹管伸缩节具有位移补偿能力强、不漏水、安装方便、维修简单、运行可靠等优点，20世纪90年代后逐渐取代套筒式伸缩节，在我国很多水电站和引水工程中得到了应用[1]。虽然波纹管伸缩节在水利水电行业已有十多年的发展，但目前积累的经验、运行参数和反馈信息还不全面，其设计、制造水平也有待提高[2]。

目前波纹管伸缩节的设计主要参照GB/T 12777—2008《金属波纹管膨胀节通用技术条件》[3]和《美国膨胀节制造商协会标准》[4]进行，设计过程非常复杂，需要对耐压能力、位移引起的应力、疲劳寿命、结构的刚度和稳定性等进行计算和校核。由于波纹管形状复杂，计算公式假定和简化较多，很难了解波纹管实际受力情况。目前进行管道应力分析时波纹管多采用等效直管模型，即用一个轴向刚度相等的直管段代替波纹管以简化计算，很少探究波纹管的真实工作状态[5-7]。此外，波纹管一般采用不锈钢制作而成，该材料比例极限较低，具有明显的塑性特征，传统的设计方法和等效模型也很难考虑材料的非线性。而有限单元法可以建立细致的三维模型，考虑材料非线性、接触非线性等因素，近年来在波纹管伸缩节的研究中得到了应用[8-10]。但目前的研究多针对波纹管的疲劳寿命、内压承载力和刚度等问题进行，对波纹管的位移补偿能力研究较少，模型中对波纹管之外的构件也进行了简化。文献[11]建立了Ω形波纹管波纹的局部模型，对内压和轴向力的承载极限展开了研究，但研究中波纹管的应力采用允许应力控制，在极限荷载下材料基本上未达到屈服状态，计算结果也未能真正体现波纹管的极限承载能力。

水利水电工程所用的波纹管伸缩节一般规模较大，除了要承受较高的内压外，对不均匀变位的补偿能力也要求较高。特别是近年来不少引水工程需穿越活动断裂带，部分断层滑移速度甚至超过10 mm/a，管线中需布置较多波纹管伸缩节适应活动断层的大变位。例如，云南掌鸠河引水供水工程管线穿越普渡河断裂带，450 m长管线内布置10套复式波纹管伸缩节，设计允许轴向和径向变位均为100 mm。由于活动断层运动的不确定性和发生强震的可能性，伸缩节承受的变形量可能超出设计值。基于上述背景，本文结合某引水工程，建立了波纹管伸缩节的三维有限元模型，施加不同模式的位移荷载，对波纹管伸缩节的极限承载能力进行了非线性有限元分析，以期为相关工程和波纹管的设计应用提供参考。

1 有限元模型与计算荷载

该引水工程为跨活断层倒虹吸结构，管线长287 m，共布置7套复式波纹管伸缩节，最高水头39 m，预计未来百年内水平和垂直累计位移量分别约为(1.63±0.67)m和(0.99±0.45)m，结构设计使用年限30年。伸缩节采用复式铰链型伸缩节，波纹管采用无加强U形波纹管，设计轴向和横向补偿量为100 mm，波纹管单层名义厚度2 mm，共2层，长孔铰链板限位值为150 mm。伸缩节由中间管所连接的2个波纹管及十字销轴、铰链板、立板、加强环和加劲板等结构件组成，能吸收任一平面内的横向位移并能承受压力和推力，铰链两侧的销轴起限位作用，所留有的活动间隙不妨碍正常使用条件下波纹管的各向位移，但能限制波纹管发生过大变形。伸缩节及限位装置如图1所示，波纹管的几何尺寸如图2所示。

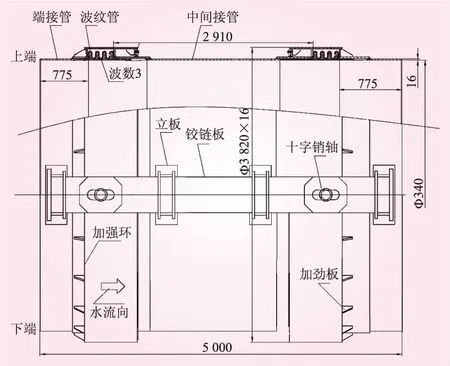
图1 复式铰链型波纹管伸缩节(单位：mm)

图2 波纹管几何尺寸(单位：mm)

根据波纹管设计参数，建立了包括波纹管、中间接管及端接管、加劲环、加劲板、主副铰链板等在内的三维有限元模型。其中，波纹管材料采用奥氏体不锈钢304，中间接管及端接管为Q345R钢材，采用壳单元模拟；主铰链板、副铰链板及立板均采用Q235-B钢材，销轴采用35号钢材，采用实体单元模拟。主副铰链板之间、销轴与主副铰链板之间建立接触对来模拟其接触传力关系。模型共剖分单元数26 153个，节点数34 693个，如图3所示。为了进行对比，将图3所示伸缩节模型中限位的铰链板、立板等构件去掉，对自由型波纹管伸缩节也进行了分析。本文主要针对位移进行极限分析，计算中首先施加重力、水压力，然后波纹管一端固定，另外一端施加不同模式的位移，各位移模式包括轴向压缩、轴向拉伸、竖向剪切、压缩+剪切，拉伸+剪切。对于组合位移模式，各位移分量在加载中保持相等。

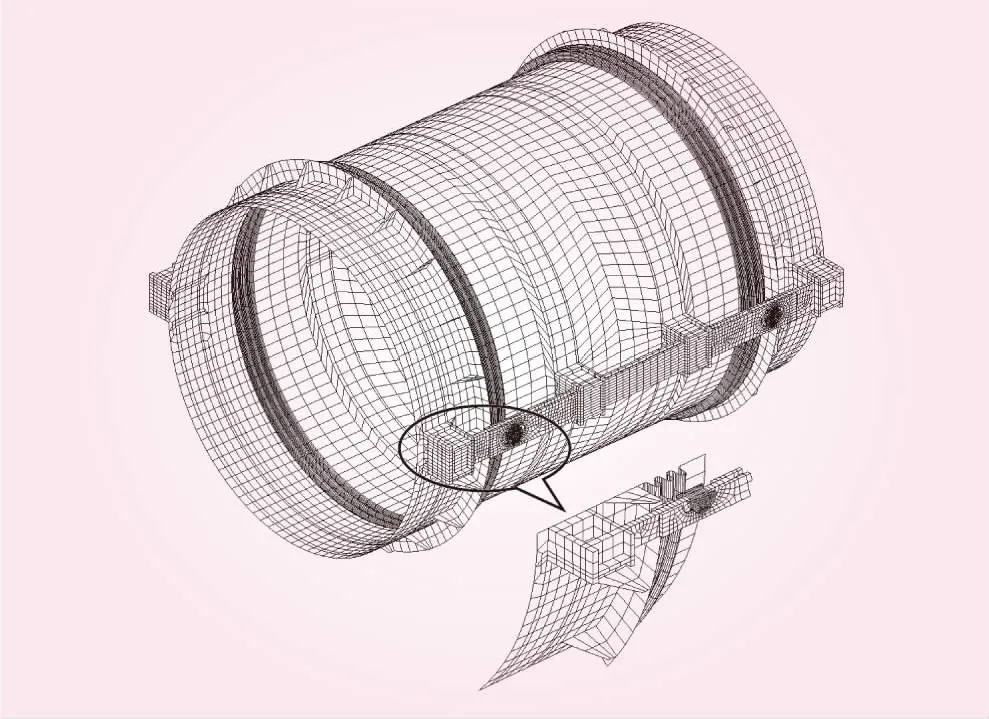
图3 波纹管伸缩节有限元模型

2 波纹管伸缩节的非线性特性

(1)材料非线性。波纹管一般采用不锈钢材料加工而成，不锈钢属于典型的非线性材料，例如304不锈钢，比例极限较低，约为90 MPa，材料很容易进入塑性阶段。因此，在进行有限元计算时，需要考虑材料的塑性，以更好地反映结构的实际受力特征。根据304不锈钢材料的应力-应变曲线及特征强度值[12-13]，采用多线性随动强化弹塑性本构模型来描述不锈钢材料的力学特性。对伸缩节其它构件所用到的钢材，根据规范推荐，采用双线性等向强化弹塑性本构模型模拟。各钢材应力应变曲线如图4所示，屈服强度和极限强度见表1。

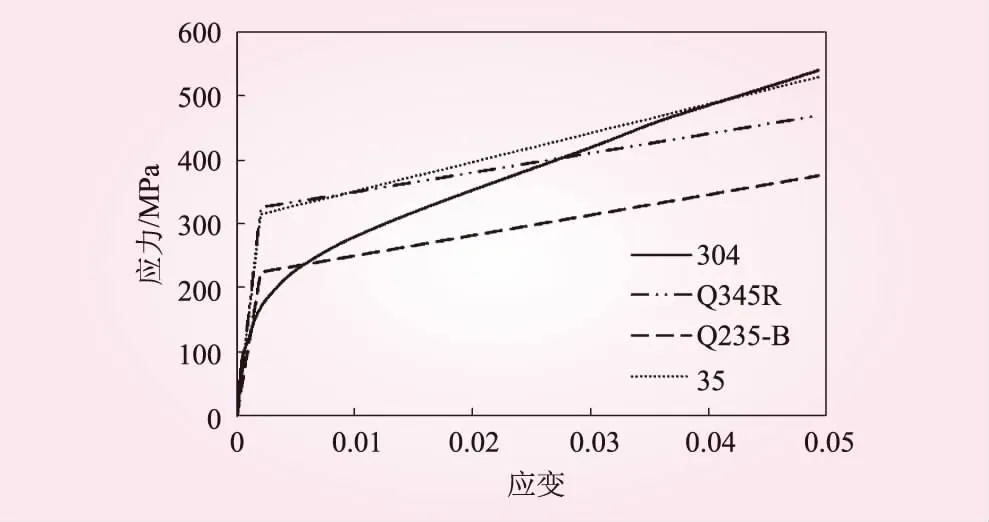
图4 钢材应力应变曲线

(2)接触非线性。当波纹管的变形较大时，铰链板将限制波纹管继续变形，主副铰链板之间、销轴与主副铰链板之间出现相互挤压、滑移，由此也会产生法向压力和切向摩擦力，这种相互作用属于典型的接触非线性行为。本文运用通用有限元软件ABAQUS进行有限元计算，建立面-面接触对来模拟波纹管伸缩节中的接触非线性行为，接触对允许有大滑动，接触面切向采用库仑摩擦模型来模拟其切向力学行为。

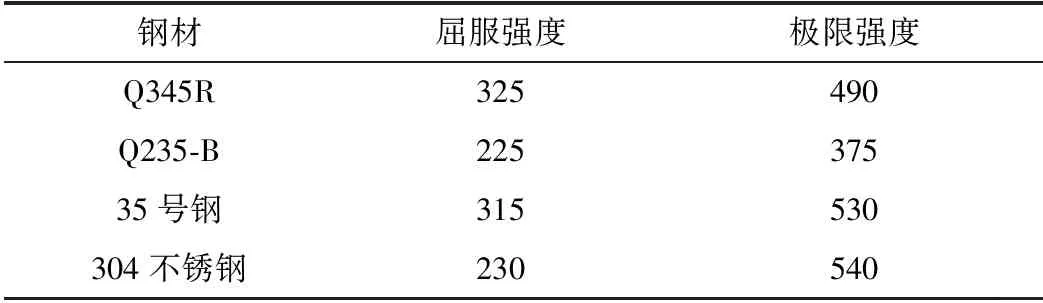
表1 各钢材的强度 MPa

(3)几何非线性。波纹管伸缩节的刚度很小，在荷载作用下结构容易产生大的横向位移和转动，由于P-Δ效应产生附加弯矩，使得系统变形进一步加剧。该问题为典型的几何非线性问题，因此几何方程的建立需基于结构变形后的状态。该类问题的研究需要用到大变形理论，本文运用ABAQUS进行有限元计算时，通过激活几何非线性选项nlgeom的开关对大变形加以考虑。

3 波纹管伸缩节极限能力分析

波纹管伸缩节有2个基本受力特点：①局部区域应力较高，最先达到屈服状态，例如波纹管波峰和波谷处的应力一般远高于其他部位，局部区域的塑性屈服，并不至于造成结构的强度破坏，结构还能继续承载；②钢材的塑性较好，特别是制作波纹管的不锈钢材料，在应力达到屈服强度后，应力还可以有明显的增大过程，直至达到极限强度。基于上述特征，同时为便于分析，本文将波纹管伸缩节的应力状态划分为2个阶段：应力达到屈服强度为第一极限状态，材料开始进入屈服状态，将产生较大的变形；应力达到极限强度为第二极限状态，材料进入破坏阶段。波纹管伸缩节应力率先达到屈服强度和极限强度的区域范围非常小，因此本文以出现较大的连通的塑性区或极限应力区作为标准来判断结构是否进入第一极限状态或第二极限状态。限于篇幅，仅以压缩位移模式为例阐述波纹管伸缩节的受力及破坏过程，其他位移模式仅给出相关结论。

3.1 自由型波纹管伸缩节极限能力分析

以压缩位移模式为例，根据非线性有限元计算结果，波纹管波峰和波谷特征点表面应力随位移的变化曲线如图5。从图中可以看到，在自重和内水压力作用下，波纹管波峰和波谷特征点表面应力已达到80 MPa；波纹管受到挤压后，波峰和波谷受弯较为严重，产生较大的表面应力，在压缩位移接近120 mm时，波纹管波峰和波谷的应力已达到屈服强度，如图6a中黑色区域所示，波纹管进入第一极限状态。随着压缩位移的增加，波纹管表面应力继续增大，当压缩位移接近300 mm时，波谷的表面应力达到了极限强度。随着位移的继续增大，应力达到极限强度的区域不断扩展，在位移达到340 mm时，波纹管已形成了贯通的圆周形极限应力区，波纹管伸缩节进入第二极限状态，如图6b所示。

图5 自由型伸缩节特征点应力-位移曲线

图6 受压时伸缩节进入极限状态的区域

对自由型波纹管伸缩节，在没有限位装置的情况下，波纹管变形大，而中间接管、端接管由于刚度较大，变形很小，应力一般不会达到相应钢材的屈服强度和极限强度，因此波纹管先于其他构件破坏。

表2列出了自由型波纹管伸缩节在各位移模式下极限状态对应的位移量。从表2中可知，各位移模式下，位移在(100～120)mm间波纹管达到第一极限状态。对于单向位移模式，位移量达到310 mm之后，波纹管才进入第二极限状态，进入破坏阶段；对于组合位移模式，位移量达到250 mm后，波纹管就进入第二极限状态。比较各单向位移模式可以发现，拉伸模式下波纹管的受力状态最差，压缩次之，竖向剪切相对最好，且破坏区域集中在管顶和管底附近2个区域(见图7)。组合模式下，波纹管能承担的极限位移量明显减小。总体而言，与波纹管设计位移量相比，波纹管具有较高的安全储备。

表2 自由型伸缩节极限状态对应位移量 mm

图7 受剪时伸缩节进入极限状态的区域

3.2 铰链型波纹管伸缩节极限能力分析

实际工程中，为了保护波纹管，通常会设置相应的限位装置，避免波纹的过度变形，本文对设置了限位装置的铰链型波纹管伸缩节进行位移补偿极限能力分析。以压缩位移模式为例，根据非线性有限元计算结果，整理波纹管波峰和波谷特征点表面应力随位移的变化曲线如图8所示，结构约束端水平方向反力随压缩位移的变化曲线如图9所示。

图8 铰链型伸缩节特征点应力-位移曲线

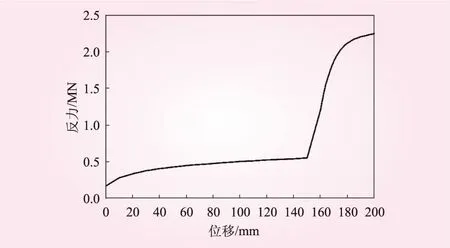
图9 约束端水平反力-位移变化曲线

对比图5可以看出，当施加的压缩位移小于伸缩节限位值(150 mm)时，特征点的应力与自由型波纹管伸缩节基本一致。在这个阶段，伸缩节上的链板通过销轴自由滑移来适应压缩变形，链板不会变形，伸缩节变形和应力状况与自由型波纹管伸缩节基本一致，主要表现为波纹管受到压缩产生较明显的变形和较大的应力，其他构件应力很小；当压缩超过限位值后，销轴自由滑移已达极限，位移继续增加时，管道的变形大于链板，链板及两端的立板将向外弯曲变形，产生较大的弯曲应力，约束端反力也随位移的增加迅速增大，如图9所示。

由于波纹管的屈服强度较低，当压缩位移为120 mm时，波纹管首先进入第一极限状态，与自由型波纹管伸缩节相同；当压缩位移为168 mm时，链板出现较大区域的屈服(见图10a)；当压缩位移为200 mm时，链板应力大范围达到极限强度，链板附近的局部管道应力也达到极限强度，可以认为链板达到第二极限状态，进入破坏阶段(见图10b)，而此时端接管、中间接管及波纹管应力均未达到极限强度。可见在设置了限位装置的情况下，在承受压缩位移时，链板更易先于波纹管而破坏。

图10 受压时链板进入极限状态的区域

伸缩节在有限位装置的情况下，当位移荷载小于伸缩节限位值时，销轴的自由滑移可吸收位移，变形和应力状况与不设限位装置时基本一致；当位移荷载超过限位值时，销轴自由滑移已达极限，链板将发生弯曲，产生较大的弯曲应力。因此在轴向位移荷载模式下，链板先于其它构件破坏。而在剪切位移及组合位移模式下，以波纹管的变形为主，链板等其他附件应力很小，波纹管将率先破坏。表3列出了有限位波纹管伸缩节在各位移模式下极限状态对应的位移量。从表中可以看出，在各位移模式下，均是波纹管先于链板进入第一极限状态；在轴向位移模式下，链板先于波纹管进入第二极限状态，而在组合位移模式下，波纹管则先进入第二极限状态。对于轴向位移，铰链板破坏的位移限值在200 mm左右，对竖向剪切及组合位移模式，波纹管破坏的位移限值与自由型波纹管伸缩节接近。总体而言，相对于100 mm的设计补偿量，伸缩节具有较高的安全储备。限位装置的强度也应有所保证，避免因限位装置强度不足导致波纹管伸缩节提前破坏。

表3 铰链型伸缩节极限状态对应位移量 mm

注：括号内为位移出现位置。

4 结 论

(1)波纹管伸缩节的承载极限能力与伸缩节是否有限位装置有关。伸缩节在没有限位装置的情况下，波纹管通常最先达到屈服强度和极限强度而破坏，波纹管在各种位移模式下极限承载能力均较高，可达设计值的2～3倍。伸缩节在有限位装置时，在轴向位移模式下，链板先于其他构件而破坏，而在剪切位移及组合位移模式下，链板等其他附件应力很小，此时伸缩节的极限位移补偿能力取决于波纹管的极限承载能力。

(2)波纹管伸缩节在各类位移荷载作用下，以波纹管和铰链板等构件的局部屈服和局部破坏为主，因此结构具有较高的极限承载能力。无论伸缩节有无限位装置，各位移模式的位移量达到200 mm后，波纹管才进入破坏阶段，相比于100 mm的位移设计值，伸缩节具有较高的安全储备。

(3)伸缩节的设计中应注意限位装置限位值和强度在合理范围内，避免因限位装置约束过强或强度不足导致波纹管伸缩节提前破坏。