基于灵敏度分析的区间不确定性稳健设计

许焕卫 李沐峰 王 鑫 胡 聪 张遂川

电子科技大学机械与电气工程学院，成都，611731

0 引言

在工程实际中，复杂技术装备在设计和优化时，目标函数和约束条件通常都不是线性的。更为困难的是，一些信息通常情况下是匮乏的、不确定和不精确的，如温度、应力、零件形状尺寸、操作方式和运行轨迹等的变化，以及建立数学模型时由于认知所限带来的误差等。这些不定因素的存在往往导致复杂技术装备的性能对不确定因素更加敏感，性能波动几率大大增加，进而影响产品的质量。另外，在设计和优化的过程中往往涉及多种因素，如果全部考虑，不仅会使问题复杂化，还会浪费大量资源。由此，有必要筛选出对产品性能影响较大的因素着重考虑，同时适当忽略影响较小因素的不确定性。

稳健设计理论因具有抗干扰的属性，现已被广泛地应用在各领域中[1-3]。稳健优化主要包括两大类：第一类是概率稳健优化，该类方法需知道输入参数的概率分布，概率稳健优化被应用到可靠性优化[4]、协同优化[5]、分析目标级联(ATC)策略中[6]，然而，这些稳健设计优化仅适用于有连续目标函数和约束函数的单目标优化问题，且往往是一种特定的情形，如文献[6-9]；第二类是以区间分析方法为主的非概率稳健优化[10-13]，因其只需获得输入参数的取值区间，而无需确切的分布，故区间分析有很强的适用性。

灵敏度分析[14](sensitivity analysis，SA)的最终目标是识别输入的可变性对输出变异性的贡献。阮文斌等[15]将基于方差和基于失效概率的全局灵敏度分析方法用到复合材料结构中，成功分析了随机输入变量对复合材料模型输出响应量(最大位移和临界强度比方差)的贡献大小以及对两个响应失效概率的影响；张义民等[16]提出了单自由度振动系统的可靠性灵敏度分析方法，放松了对随机参数的分布类型和激励类型的限制；CANNAV[17]在总结现有灵敏度分析方法的基础上提出了一种基于灵敏度的模型选择准则，并将该准则成功应用到火山源模型的量化拟合中；HAMEL等[18]提出了一种基于多目标的区间不确定下灵敏度分析的改进设计方法，可以在确保可行性的条件下对随机变量进行轻微调整；邱志平等[19]利用区间扩张理论及其性质定义了结构区间的相对和绝对灵敏度，可在不求导的条件下通过区间运算求得变量灵敏度值，降低了灵敏度求解难度。

由上述可以看出，灵敏度分析被广泛地应用到各领域中，但是传统灵敏度分析的精确度依赖于数据的完整程度。本文为解决产品优化设计过程中信息少、涉及因素多等难点，利用稳健设计及灵敏度分析和区间不确定理论的优越性，提出基于灵敏度分析的区间不确定性稳健设计方法。该方法的优势在于：不仅能在设计之初筛选出对产品性能影响较大的因素，而且还可以选择性地忽略影响较小因素的不确定性，进而取得性能函数稳健的效果。

1 灵敏度分析

灵敏度分析[20-21]能够反映某一或某几个参数变化或外界噪声对系统输出的影响程度。

1.1 全局灵敏度分析——Sobol’法

全局灵敏度分析就是综合考虑输入变量对性能函数的整体影响，进而掌握非单调、非线性、非叠加的性能函数整体特性。在全局灵敏度分析方法中，Sobol’法[22]是目前常用的方法。设空间单元体为Ω(k)，输入为k维，表示为

Ω(k)={x|0≤xi≤1;i=1,2,…,k}

(1)

Sobol’法的关键步骤在于将性能函数f(x)准确地转化为

(2)

式(2)中共有2k个子项，采用多重积分进行分解。式(2)中，f0是常数，其余各项对其所包含的每一个因素的积分为0，即

(3)

式(3)的各个子项彼此正交，即

(4)

式(2)中的分解唯一，且各阶子项均可通过多重积分运算得到，即

(5)

式中，x-i为去除xi之后的其他变量；x-(ij)为去除xi和xj之后的其他变量。

同样可类比得到其他高阶子项。从而模型f(x)的总方差为

(6)

则式(2)中的各阶偏方差可表示为

(7)

i1,i2,…,is=1,2，…,k

对式(2)在整个Ω(k)域先平方后积分，再结合式(4)可得

(8)

那么s阶的灵敏度为

(9)

此处Si是因素xi的一阶灵敏度系数，反映了因素xi对性能函数f(x)的主要影响程度，Sij(i≠j)为二阶灵敏度系数，用来表述两参数交叉对性能函数的共同影响程度。依此类推，S1,2,…,k反映了k个因素之间的彼此交叉影响。

总效应指数是指因素xi对性能函数f(x)整体影响程度，常用来评价单个参数对性能函数的全部影响。

由式(8)可知

(10)

1.2 Sobol’ 法计算简化公式

Sobol’法概念虽然简单，但求解却十分困难，因此可由蒙特卡罗积分法进行化简，则式(6)、式(7)中的f0、D及Di，可简化为

(11)

x(-i)m={x1m,x2m,…,x(i-1)m,x(i+1)m,…,xkm}

(12)

式中，n为蒙特卡罗估计的采样数；xm为Ω(k)空间的采样点；上标(1)、(2)代表x的两个n×k维采样数据。

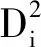
2 不确定性分析

工程实际中各种不确定性因素的变化将导致复杂技术装备的性能不稳定，甚至会导致重大的损失。传统方法通过提高制造精度等手段来保证产品质量，但因代价过大往往不可取。不确定性优化方法主要有随机规划[23]和模糊规划[24]两类，然而，在实际应用中，由于信息不完整使得这两类方法有较大的局限性。区间数优化因其所需信息少，操作便捷，故与工程实际有优良的匹配性，成为一种新的不确定性工程优化方法。

2.1 区间不确定性分析

根据区间分析[25]，区间模型可以定义为

AI=[AL,AR]={x|AL≤x≤AR,x∈R}

(13)

式中，上标L、R 、I分别表示区间下界、区间上界、区间,当AL=AR时，区间退化为一实数a。

区间还可定义如下：

AI=〈Ac,Aw〉={x|Ac-Aw≤x≤Ac+Aw}

(14)

其中，Ac和Aw分别为区间AI的中点和半径，它们的关系如图1所示。

图1 区间的几何描述Fig.1 The geometric description of interval

定义γ(AI)为区间AI的不确定性水平，表达式为[26]

(15)

2.2 区间可能度及区间可能度转换模型

因区间表示的是一个范围，因此需要进行相应转换以判断大小及优劣。文献[27]给出了一种区间可能度关系的计算式：

P(AI≤BI)=

(16)

在区间BI退化为一实数b的情况下，有如下新的可能度关系：

(17)

同理,当区间AI退化为一实数a时，有如下可能度关系：

(18)

图2、图3、图4分别为式(16)、式(17)、式(18)所对应的几何描述。

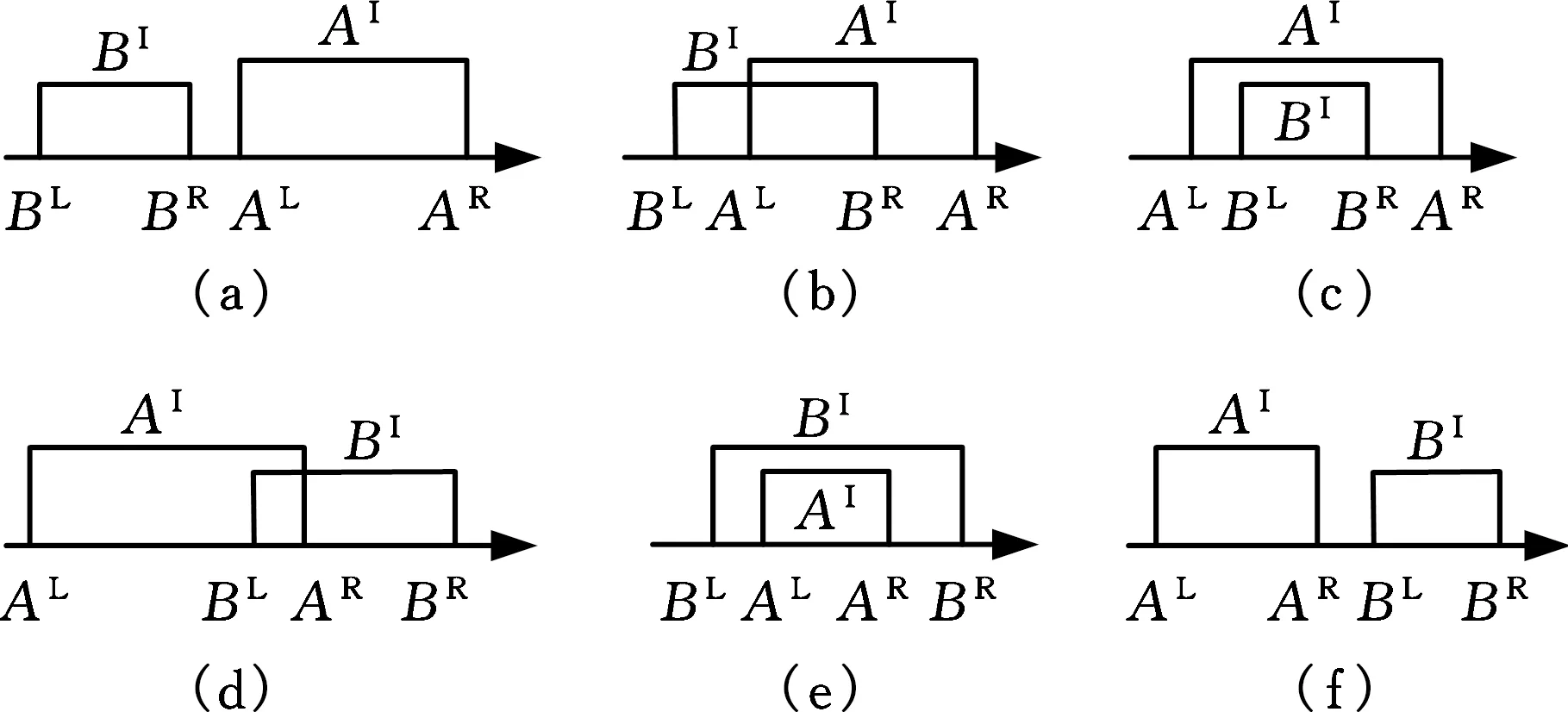
图2 区间AI和区间BI所有可能的位置关系Fig.2 All possible position relationships of interval AI and BI

图3 区间AI和实数b可能的位置关系Fig.3 The possible position relation of interval AI and real b

图4 实数a和区间BI和可能的位置关系Fig.4 The possible position relation of real a and interval BI

两个区间的位置关系确定后，基于区间可能度的确定性优化模型为[27]

(19)

(20)

上述稳健模型可以保证在绝对满足fI(X)≤VI的情况下，找到不确定因素对目标函数影响最小、性能最稳健、可靠的优化设计解。

3 区间不确定性稳健设计

当前的工程问题日趋复杂，通常需考虑众多因素，且已知的设计信息较少。这种情况下，传统优化方法因考虑太多因素而导致计算繁杂且效率不高。本文通过整合全局灵敏度分析、不确定分析、稳健设计方法，构造了基于灵敏度分析的区间不确定性稳健设计框架。具体步骤如下：

(1)根据设计信息建立传统优化数学模型。

(2)对目标函数f(X)和重要的约束条件g(X)运用Sobol’理论进行灵敏度分析，求出第i个设计变量xi对应的目标函数和重要约束条件的灵敏度值Si。

(3)若Si≤ε(ε值根据实际工程需要而定)，则对应的设计变量xi可设置为常数a，否则对其进行区间分析，确定其取值区间AI，令xi=AI。

(4)利用区间分析改进常规优化模型，利用式(20)建立区间可能度稳健设计模型，从而达到鲁棒效果，采用双层嵌套理论[27]求解所建立的区间可能度模型。

(5)判断得到的稳健解，如满足目标函数输出区间与理想值之间的最大误差δ<0.1的条件，则程序结束，否则返回步骤(3)重新分析不灵敏项。

该框架可以有效解决灵敏度分析中对随机变量信息完整度的高要求问题，又可以在区间不确定分析中，降低影响较大因素因波动太大造成的影响。该优化框架可以避开影响较小因素的干扰，重点考虑影响较大的因素，有效降低设计变量维度，因此能够大大降低模型复杂度，有效缩短计算时间。另外，因为该模型最终输出为一功能区间，因此还可以在乏信息、乏数据的产品设计初期当做预测模型来预测产品的性能，为进一步地优化提供参考。图5为基于灵敏度分析的区间不确定性稳健设计框架及求解流程图。

图5 流程图Fig.5 The flow chart

4 工程实例

该工程实例来源于文献[28]，设计车辆的某型转向机构，示意图见图6。各设计变量相互独立且服从正态分布。设计变量为轴距L、主销中心距B、转向梯形臂长l、梯形底角θ。不确定参数为运动副间隙r1～r4。运动副间隙r1～r4在相应区间上相互独立且正态分布。相关设计信息如表1所示。

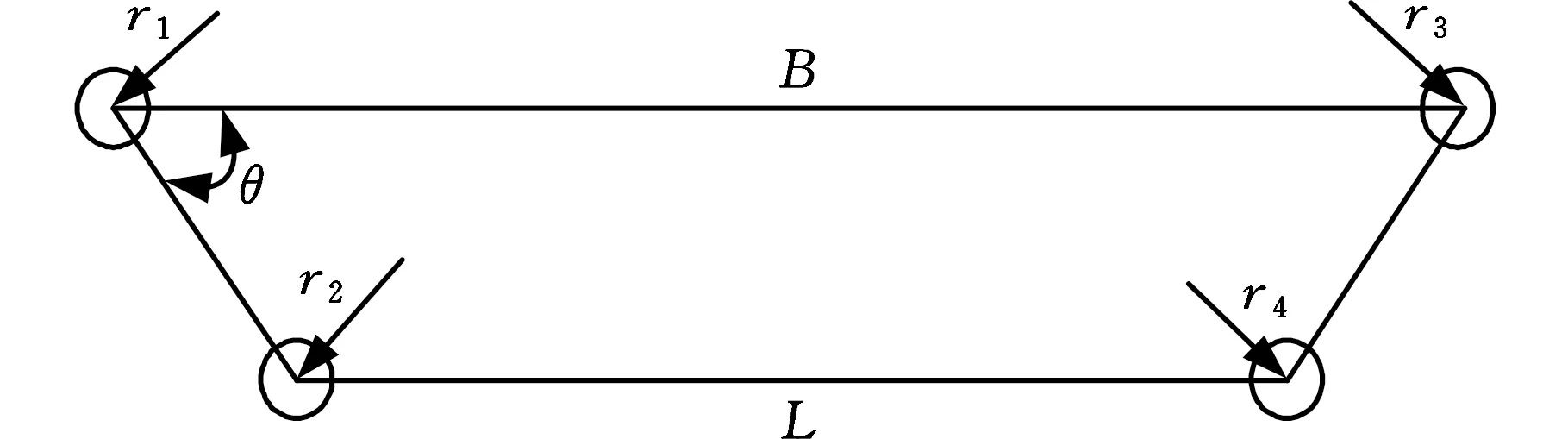
图6 考虑间隙的汽车转向机构示意图Fig.6 Steering Trapezoidal Structure Considering Motion Pair Clearance表1 设计信息Tab.1 Design information

设计变量L(m)B(m)l(m)θ(°)标准差σ0.020.010.010.05均值μ3.652.30.2567不确定参数r1(mm)r2(mm)r3(mm)r4(mm)变化区间(0.5,1.5)(0.2,0.8)(0.5,1.5)(0.2,0.8)

根据相关设计要求,各个设计变量的边界约束条件为：3.5 m≤L≤3.7 m，2.2 m≤B≤2.5 m， 0.125 m≤l≤0.5 m；根据设计信息可知，在整个转向过程中转向机构的运动误差不能超过3°，并将其设为极限函数，要求其可靠度R≥0.99。当内侧转向轮的转角为β(通常小于20°)时，外侧车轮偏转角

α0=f0(β)=arccot(cotβ+B/L)

(21)

根据图6所示的转向机构，实际的外向车轮偏转角

(22)

将各相邻杆件间的配合间隙值代入式(22)，就可以得到实际的外向车轮偏转角。

4.1 目标函数确定

转向机构的转向精度是衡量转向机构性能好坏的一个重要指标，本文将其作为目标函数。在内侧车轮转角β从最小角度0°转到最大角度20°的过程中，外侧车轮的理想转向角与实际转向角之间应尽可能保持一致，即

(23)

式中，α0i为理论值。

在满足设计要求的前提下，式(23)可以保证实际值的波动在尽可能小的同时最接近目标值，也就是保证目标函数的方差和均值同时尽可能小。

4.2 重要约束条件

当外侧车轮的转角误差过大时，轮胎的磨损将加剧，为此有

g1(x,r)=|αi-α0i|≤3°

(24)

式中，x为设计变量；r为不确定性参数，体现在相应的杆件中。

在转向机构中，横拉杆和转向梯形臂之间的夹角是一个变化的值，该夹角的最小锐角被称为最小传动角。最小传动角过大将会导致转向机构的各个杆件之间出现“死点”， 最小传动角过小又会导致各个杆件受力过大，进而对杆件的强度要求也会相应提高，因此最小传动角的计算公式如下：

g2(x,r)=

(25)

其中，γmax为最大极限转角。计算得到的最小传动角范围为30°～50°。

转向梯形角约束如下：

(26)

除上述3个约束外，还有设计变量及不确定性变量的边界约束。

建立如下一般设计模型：

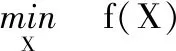
s.t.g2(x,r)-3°≤0

30°≤g2(x,r)≤50°

0°≤g3(x,r)≤5°

2.2 m≤B≤2.5 m 3.5 m≤L≤3.7 m

0.125 m≤l≤0.5 m

r1∈(0.000 5,0.001 5)mr2∈(0.000 2,0.000 8)m

r3∈(0.000 5,0.001 5)mr4∈(0.000 2,0.000 8)m

接着对目标函数f(X)、重要约束条件g2进行灵敏度分析(g1可包含在目标函数中，g3涉及的参数过少不必进行灵敏度分析),结果如表2所示。

表2 灵敏度分析Tab.2 Sensitivity analysis

综合分析表2数据可以看出，当ε=0.05时，对目标函数而言，因SL+∑Sri=0.03，小于0.05，故在目标函数中均可忽略其不确定性而设为常值；同理在约束函数g1中因SB+SL+∑Sri=0.025 6，小于0.05，则设计变量B、L及不确定因素r1～r4的不确定性均可忽略而设为常值。表中某些参数灵敏度值为0是因为其值太小而被忽略。

利用区间分析对常规优化设计模型进行改进，可得如下基于灵敏度分析的区间不确定性稳健设计模型：

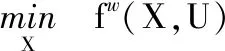
s.t.P(g1(x,r)≤3°)≥0.99

P(g2(x,r)≥[30°,50°])≥0.9

P(g3(x,r)=[0°,5°])≥0.9

2.2 m≤B≤2.5 m 3.5 m≤L≤3.7 m

0.125 m≤l≤0.5 m

r1∈(0.000 5,0.001 5)mr2∈(0.000 2,0.000 8)m

r3∈(0.000 5,0.001 5)mr4∈(0.000 2,0.000 8)m

为检验该模型可行性，设计两套方案与文献[28]所提方案及初始解做对比：方案一目标函数和约束条件中L、r2、r4为定值，即设L=3.65 m，r2=r4=0.000 5 m；方案二目标函数中L及不确定因素r1～r4均为定值，这里设L=3.65 m，r1=r3=0.001 m，r2=r4=0.000 5m。采用双层嵌套理论及粒子群算法对本文实例取自于文献[28]设计模型进行求解，得到的优化结果如表3所示。

4.3 结果分析

为验证本文所提方法，将误差考虑在内，即将两方案中非灵敏项变差的影响考虑在内时，得到内侧角β变化时(0°～20°)相对应的理论外侧转角α0、稳健设计转角α及本文所求转角区间，结果如表4所示。由表4可知，内侧转向角β从0°到20°变化的过程中，本文两种方案结果均在理想值附近。比较这两方案的最大误差，δ1max=0.070、δ2max=0.074，均小于设定值0.1，因此模型的解是合理的；不确定性水平γ1max=0.004、γ2max=0.006，说明在去除了不灵敏项的变差影响后，运用本文所提模型依然能够得到高质量解。对比两方案的求解效率，方案一由于不考虑3个变量的不确定性，求解时间平均为6.37 s，而方案二去除了5个参数的不确定性，平均求解时间为5.25 s，缩短了13.34%，说明此模型可以在有效减小计算量、简化模型复杂度的前提下提高效率；从解的质量上看，所忽略变量的总灵敏度值小于规定值时，解的精度和稳健性并不会由于舍弃这些参数而发生质的变化。由此在兼顾计算效率和计算精度的前提下，可以综合考虑工程需要与模型复杂度等因素选择去除不灵敏变量的数量。此工程实例验证了本文所提方法的正确性，且作为一个预测模型是完全满足实际工程要求的。

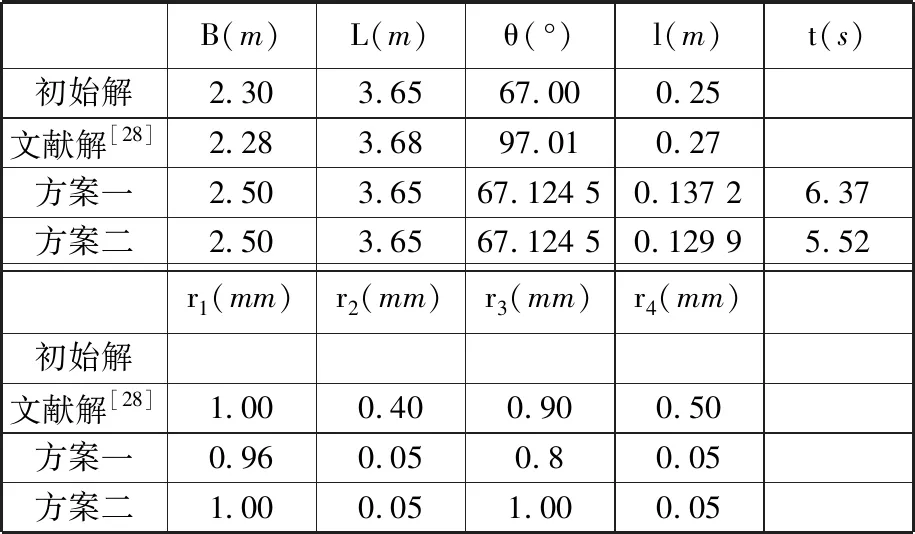
表3 优化结果Tab.3 Optimization results

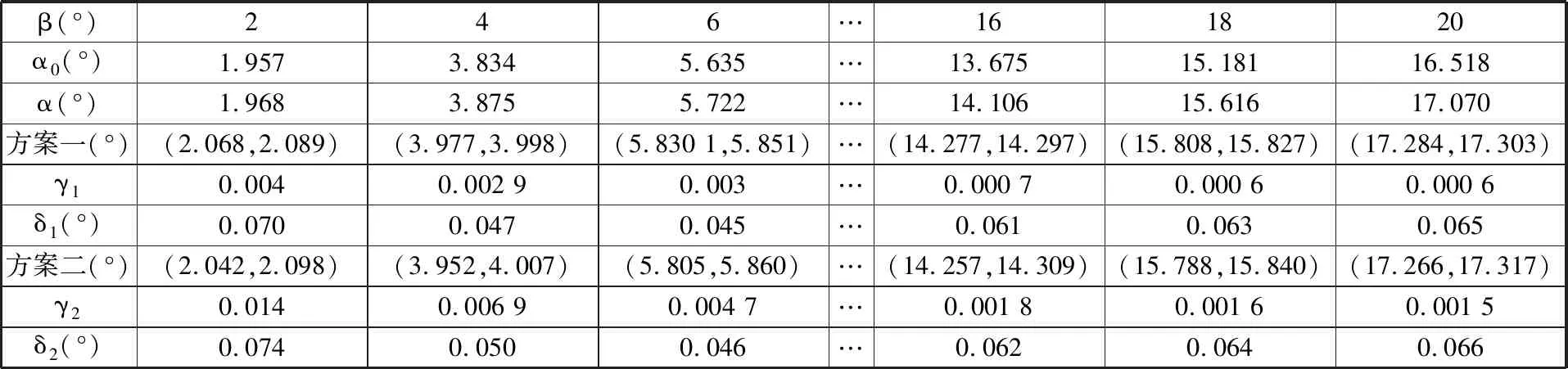
表4 结果对比Tab.4 Result comparison

5 结论

(1)利用全局灵敏度分析——Sobol’法降低模型复杂度，利用区间可能度理论量化不确定因素，进而建立了基于灵敏度分析的区间不确定性稳健设计方法。

(2)将本文所提方法应用到汽车转向机构的优化设计中，通过两种优化结果的对比分析可知，所提方法在模型精确度、复杂度、稳健性、求解效率等方面都具有一定的优势。由于最终给出的结果是一个功能输出区间，故在乏信息、乏数据的条件下，该工程稳健设计预测模型完全可以满足工程实际，为设计人员后续的进一步优化设计提供了参考。

(3)本文并没有严格定义可以舍弃其不确定性的灵敏度范围，也没有严格从数学角度推导当参数灵敏度很小时舍弃其不确定性的正确性，这些需要设计人员根据实际工程优化的具体需求而定。