面向可重构混流生产线的设施布局与生产调度并行优化方法

房殿军，黄哲昱

（同济大学 中德学院，上海 201804）

1 引言

随着“工业4.0”与“中国制造2025”等以智能制造为核心的制造业发展计划相继提出，高度灵活的大规模定制化生产模式成为制造业未来的愿景。为使生产企业具有灵活的市场响应能力，可重构制造系统（Reconfigurable Manufacturing System,RMS）得到了越来越广泛的应用。RMS是指为响应市场不规则需求的突然变化，具有能通过快速改变结构和软硬件组元来调整系统的生产能力和功能而设计的制造系统[1]。布局问题是RMS 研究的主要内容和关键技术之一，为RMS 的每个重构周期进行合理的设施布局来调整对企业的生产成本是至关重要的。

混合流水线生产（又称为混流生产）是一种常见的生产线组织形式。其通过调整生产组织的方法，在一条流水线上进行多品种搭配，有序地生产多种产品。混流生产解决了传统车间生产（Job-shop）和单件流生产（One-piece-flow）中生产效率与生产柔性的矛盾，可以获得更多的产品变化，更短的产品生命周期，更低的产品成本和更高的产能。其特征是在某些工序上存在并行设备[2]。在实际生产中，由于同工序中的并行设备存在新旧差异或型号不一致，导致其生产能力存在差距，因此调度计划通常会给不同设备分配不同的加工件上线量。

生产调度和设施布局是可重构制造系统研究的两大方向。目前对混流生产调度的大多数研究，通常仅考虑准备时间和加工时间等参数，而忽略了物流运输时间。可重构制造系统设施布局的研究则普遍集中于针对解决特定问题的算法改进，通常以设备间精确物流量作为已知量进行计算求解，忽略了实际生产中，由于并行设备之间产能不一致所导致的实际物流量与前期计划存在差异的问题。以上缺陷会对解决方案在可重构混流生产线中的实用性产生影响。

本文针对采用设施多行排列的布局，且并行设备对同一工件加工时间不相等的可重构混流生产线设施布局问题，提出了一种利用遗传算法求解最优布局和蚁群算法求解最优调度方案相结合的方法。首先根据可重构制造系统的特点对传统生产线规划流程进行改进，然后对多行布局和混流生产分别进行数学建模，并且引入路径系数减少逆向物流。接着通过数据传递和结束条件设置实现遗传算法与蚁群算法相互迭代求解。最后使用此方法对实际案例进行优化计算，结果表明了该方法具有一定有效性和实用性。

2 规划流程改进

企业在按传统规划流程进行设施布局规划时，由于在该阶段尚未进行调度计算，因此无法获得设施规划所需要的并行设备之间的精确物料搬运量。如果忽略并行设备之间的差异性，显然不可能得到最优结果。所以本文提出的优化流程是将区域内设施规划的工作转移到操作层中，与生产调度并行进行。通过布局规划算法与生产调度算法相互迭代来解决问题，从而形成一种解决可重构混流生产设施布局的优化方法，如图1所示。

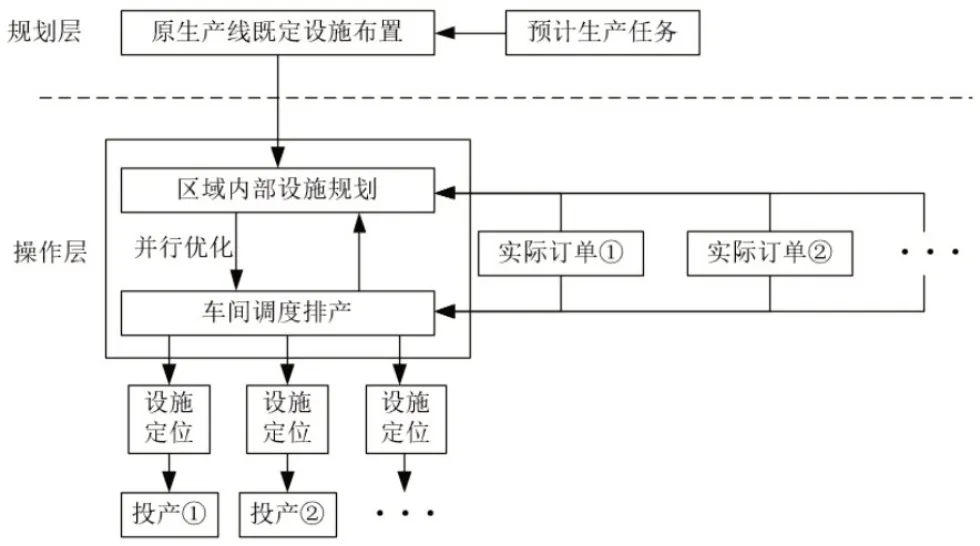
图1 改进的规划流程

3 问题建模

3.1 混流生产调度数学模型

生产调度的功能是依次对混流生产线每一道工序上的任务进行分配。首先将生产计划提交的当前工序任务集合划分为多个子任务，然后根据每个子任务的不同，以工件前往下一道工序的运输时长TTij、加工队列等待时间BTij以及设备加工时间STij的总和最小为目标，合理进行任务和机器的映射。这个问题可以模型化描述为：按照一定的策略，将m个子任务分配到 n 个加工设备上（n＜m），用表示所有待执行子任务的集合，表示加工设备的集合，限制每一个子任务和加工设备的映射关系。如式（1）所示，以矩阵TMmap表示该映射关系：

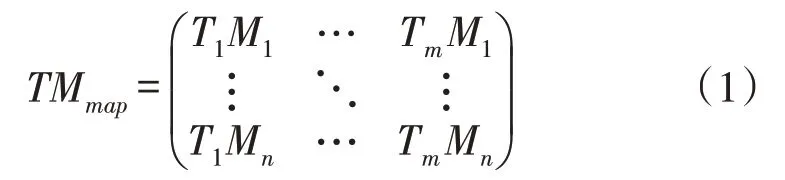
其中TmMn表示子任务和加工设备之间的对应关系。目标函数为：

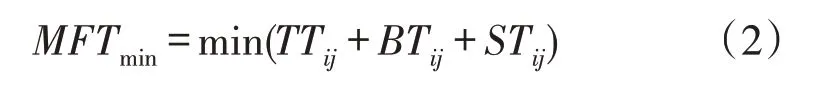
3.2 多行排列布局模型

布局遵循以下原则：以矩形表示车间和设施的形状，且矩形尺寸都已知；设施横向排列，且与车间矩形的长度方向平行；设备间横向和纵向间距已知。以车间矩形左下顶点为原点，沿矩形长度方向向右为x 轴，沿矩形宽度方向向上为y 轴建立坐标系。以设施矩形几何中心表示该设施的位置坐标。设施之间的距离由几何中心之间的最短折线距离来表示

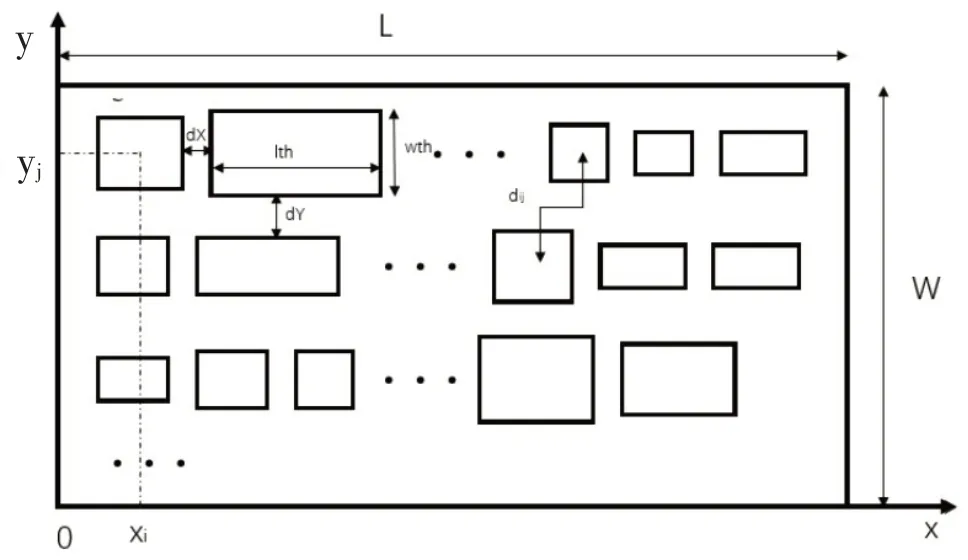
图2 多行布局位置参数示意图

目标函数为最小化物料搬运成本，见式（3），其中fij为物流量，Cdij为带路径系数的距离成本。

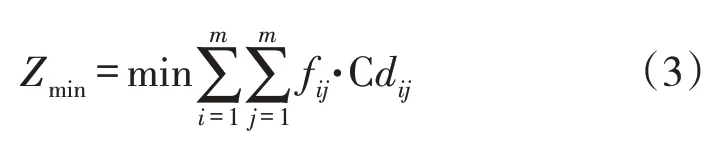
距离成本受路径方向影响，由路径系数与折线段距离共同决定。

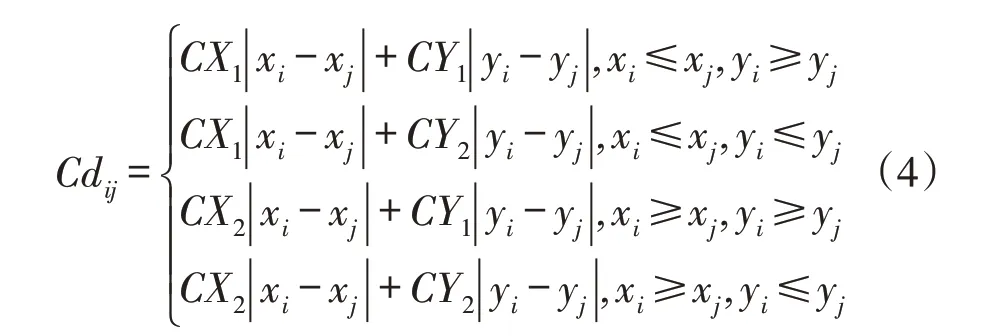
其中CX1和CX2分别为横向顺流与逆流成本系数，CY1和CY2分别为纵向顺流与逆流成本系数。规定：从车间矩形的左上顶点开始，从左向右为横向顺流（即沿x轴正方向），从上向下为纵向顺流（即沿y轴负方向）。

此外还需要设置车间边界约束，即设施不能超越车间的长和宽。设施之间不能够相互干 ，保证横纵安全间距。

3.3 设施布局与混流生产调度问题模型的耦合分析

从上述的建模过程中发现，生产调度模型以时间TTij（可以通过距离dij与已知平均搬运速度直接计算得到）作为已知量，fij作为优化变量，而设施规划模型以fij作为已知量，dij作为优化变量。从图3中可以明显地看出两个模型在数据上具有耦合性。

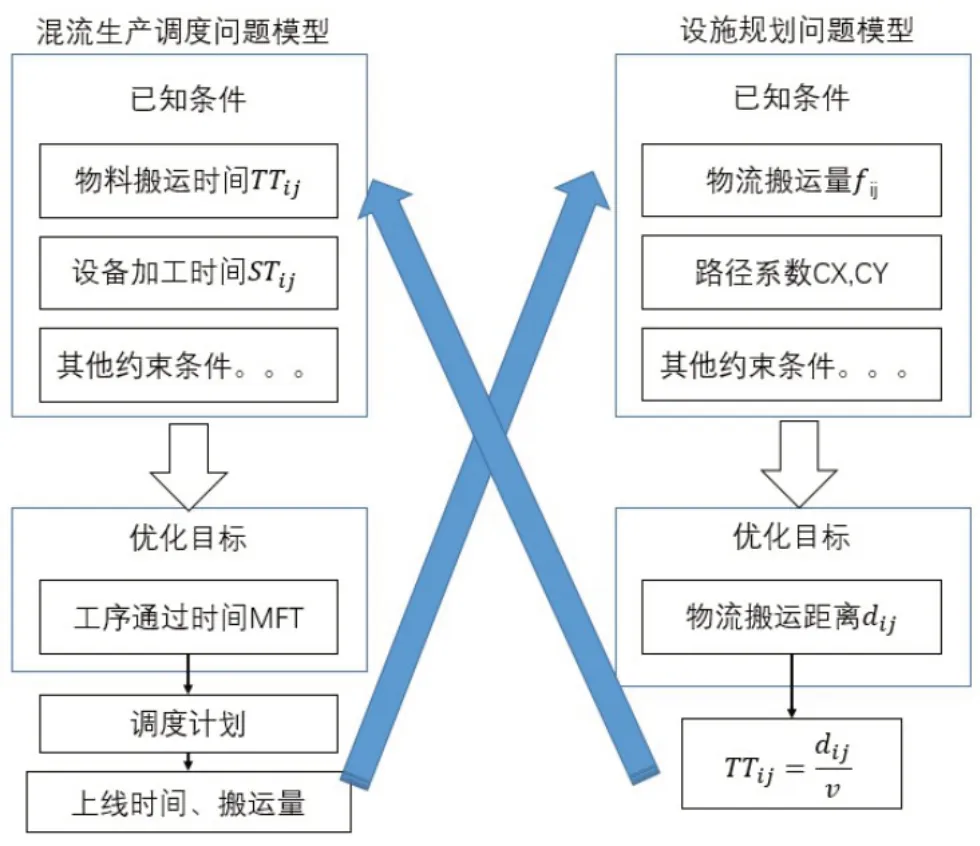
图3 模型数据的耦合关系

4 算法实现

本文针对论题提出了一个将设施布局算法与生产调度算法相互迭代运算的求解方法，其主要部分由初始解模块、迭代控制模块、设施规划模块和生产调度模块四个模块组成。每一个模块的主要功能、执行流程及逻辑关联如图4所示。

（1）初始解模块：该模块为并行算法提供初始解。根据实际应用环境的不同提供合适的初始解产生方式。

（2）生产调度模块：该模块使用蚁群算法，根据初始布局或者设施布局模块提供的布局进行调度求解，解算出调度方案中设备间物流搬运量的值，提供给设施布局模块。

（3）设施布局模块：该模块使用遗传算法，根据已知条件和生产调度模块所提供的设备间物流搬运量优化值进行求解，对布局进行优化，将解算出的设备间物料搬运的距离提供给生产调度模块。

（4）迭代控制模块：作为主函数对生产调度模块和设施布局模块进行迭代调用，并且判断迭代循环是否满足终止条件。在结构上将生产调度模块与设施布局模块嵌套在迭代控制模块之中。

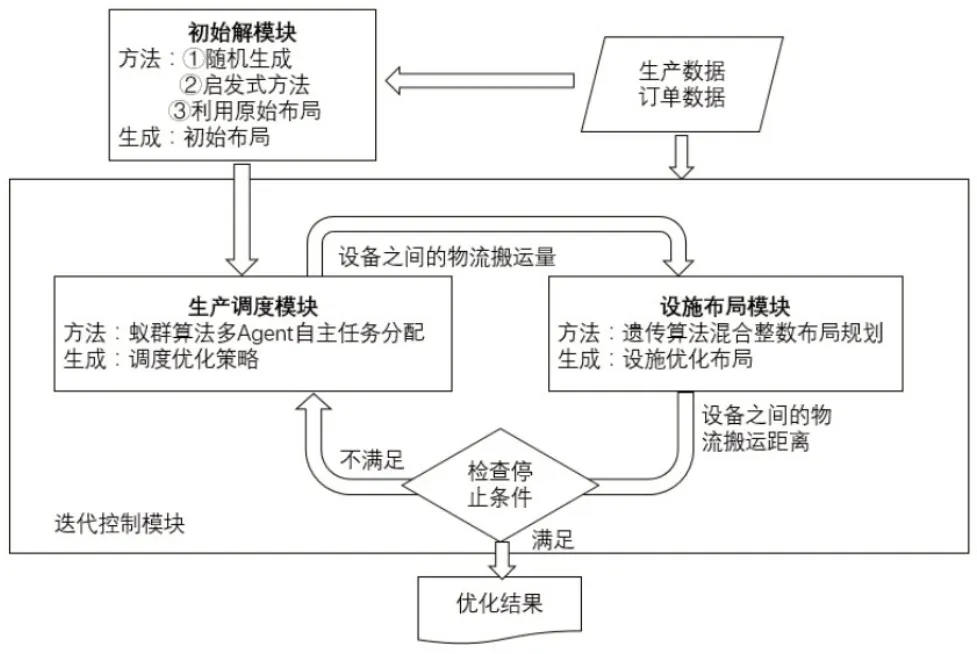
图4 并行迭代优化方法架构

4.1 初始解模块

初始解是遗传算法等优化算法执行的基础，合理的初始解通常可以加快算法的收敛速度，避免陷入局部最优。在本算例中，初始解即为初始布局，本文提出了三种可行的生成方法：随机生成、启发式方法生成和利用原有布局。其中前两者既可以用于一个全新的规划，又可以用于对现有设施进行改进，而后者只能用于现有布局的改进。

4.2 生产调度模块参数设置

生产调度模块使用蚁群算法，以工件为多代理，对每一个工件以最小工序通过时间为目标进行自主调度。

（1）路径选择概率。路径选择的概率公式如下所示：

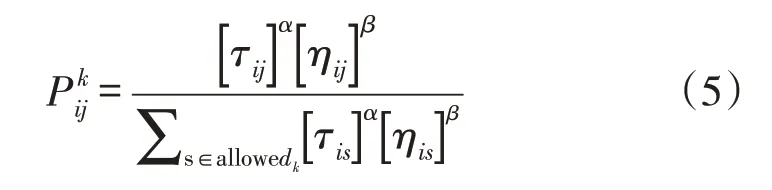
其中ηij表示子任务i 选择加工设备j 时的启发因子，它的值定义为表示第i个任务在第j个机器上的运输时长、加工队列等待时间以及设备加工时间的和，即Tij=TTij+BTij+STij。τij表示任务 i选择机器j 的信息素。α为信息素启发系数。β表示期望启发系数。allowk表示蚂蚁可以选择的下一个机位。

（2）局部信息素更新。依据如下的信息素矩阵公式（6）来完成更新。

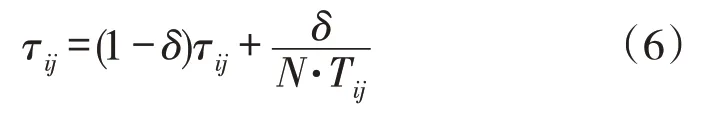
其中，δ为局部信息素挥发程度，N为该工序并行设备数量。

4.3 设施布局模块

设施布局模块采用遗传算法对布局方案进行求解。

（1）编码策略。采用布局设备几何中心的浮点数XY 坐标作为基因，由所有设备的坐标值，排列成一个染色体，来表示一个可能的布局方案：如（x1,y1,x2,y2,...,xn,yn）。

（2）适应度函数。将约束条件设计成罚函数，对约束条件采用搜索空间的限定法以适应遗传算法的需要，定义适应度函数为：

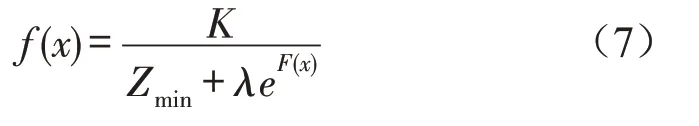
其中，K是一个常数，λ是罚函数系数，根据实际情况选取。约束条件转化F(x)函数，并对其值进行平方运算，保证其值为正。对目标函数取倒数，目的是将求解物流量Zmin最小值转化为求解适应度函数f(x)的最大值，以符合遗传算法形式多样的需要。

（3）遗传参数。遗传算法中各个主要参数的取值范围：群体大小N=20～200；交叉概率Pc=0.60～1.00；变异概率Pm=0.005～0.01。

（4）选择运算。计算群体中每一个染色体位串的适应值，将群体中各染色体按照适应度函数值排序，利用轮盘赌选择方式进行选择运算。

4.4 迭代控制模块

迭代控制模块主要起到以下三个功能：

（1）功能模块调用。迭代控制模块在编程时作为主函数，对设施规划模块和混流生产调度模块的子函数进行循环调用。

（2）功能模块间数据传递。迭代控制模块将矩阵Dist从设施规划模块传递到生产调度模块，将矩阵Flow从生产调度模块传递到设施规划模块。

（3）功能模块迭代终止判断。并行优化算法形式上是一种迭代计算方法，每进行一轮迭代都要进行算法终止判断。可以采用以下两种判断形式：①迭代次数的判定。②适应度值收敛程度判断，即当（a 为设定的收敛度常数）时则结束迭代。本文中的算例选用第一种判断形式。

算法步骤如下：

Step2：定义当前设备间距离矩阵变量为Dist，对优化对象的原始布局设施间距离进行计算，并赋值给当前设备间距离矩阵变量为Dist；

Step3：定义当前设备间工件搬运数量矩阵变量为Flow；

Step4：设当前循环次数参数N=0，最大循环次数为ξ；

Step5：以Dist以及其他相关参数为已知条件，使用蚁群算法进行混流生产线调度计算，得到工件工序通过时间较短的工件调度方案；

Step6：根据Step5调度方案中的设备间工件搬运数量对Flow赋值；

Step7：以Flow以及其他相关参数为已知条件，以A 为初始解，使用遗传算法进行求解，得到物流搬运成本较小的布局方案；

Step8：对Step7 中的优化布局方案进行编码，并赋值给A；

Step9：计算Step7中得出的优化布局方案的设备间距，并赋值给Dist；

Step10：N=N+1；

Step11：若 N ≤ξ，则返回Step5；否则，结束求解。算法流程如图5所示。

5 计算实例

某车间外形尺寸为72×30m2。内部有8个不同工序组成的加工站，编号为G1-G8，总共包含20台加工设备，编号M1-M20。每个加工站各自包含一个或多个并行设备。具体加工编号、工序名称、设备数量、设备编号、单机区域尺寸等数据见表1。

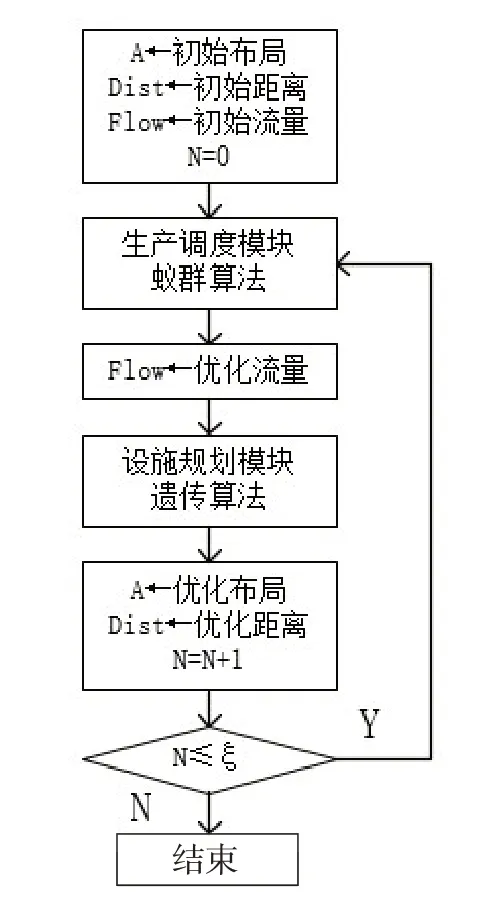
图5 综合迭代算法流程图

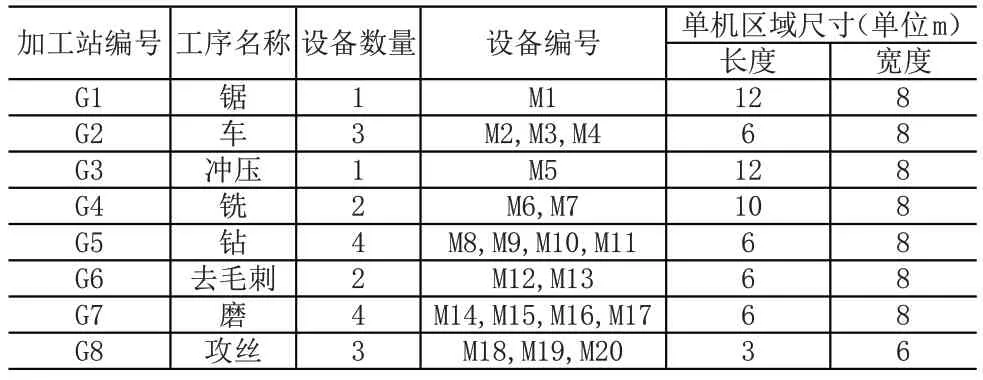
表1 工序及相应设备尺寸表

本实验使用原始布局作为优化过程的初始解。原始布局按照工序加工站顺序排列，如图6所示，设备之间的交通路径设定为：干路宽度2m，支路宽度1m。加工设备到区域边界的最小安全距离为1m。平均物料搬运速度为1m/s。

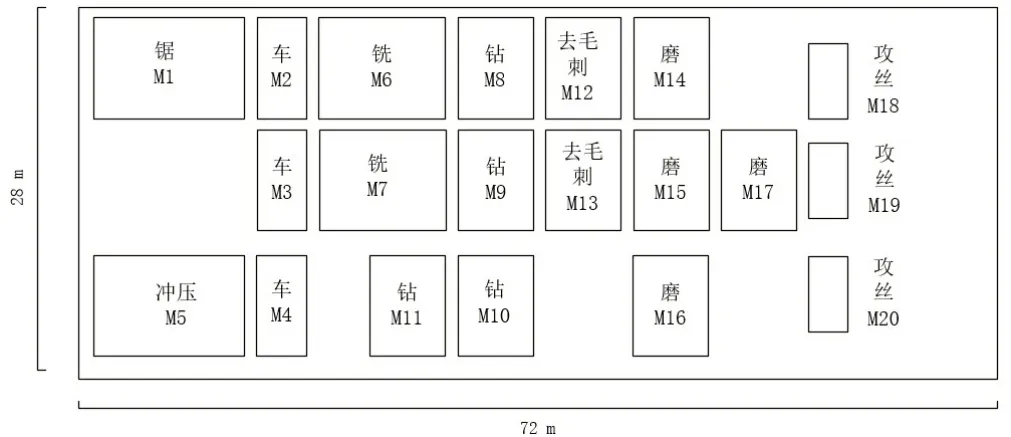
图6 车间原始布局

该车间生产5种零件，其工序如图7所示。

五种零件在各台设备上的加工时间见表2，单位为分钟。其中0 表示该工件没有相应的加工工序。工件等待时间通过记录仿真过程中各个工件在各个加工设备的前置Buffer中的滞留时间得到。

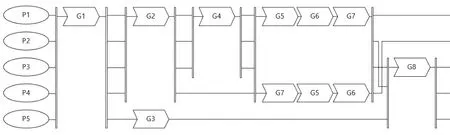
图7 产品工序流程

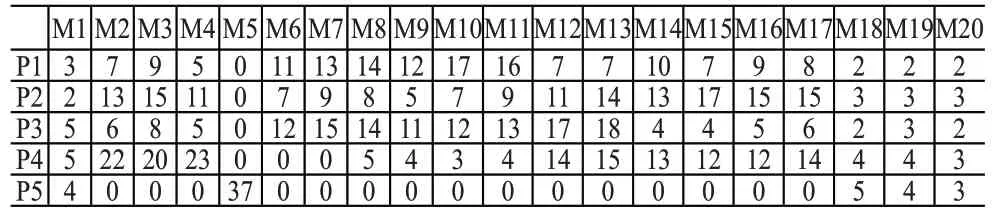
表2 工件在设备上的加工时间

由于采用了横向分行结构，导致纵向物流成本会明显大于横向物流成本，同时也要兼顾尽可能减少逆向物流，由此设置 (CX1,CX2,CY1,CY2)=(1,-3,3,-9)。使用并行优化算法运算10次后选取较优的两个结果进行观察，分别为76 458和76 461，两个结果非常接近，而在第二个结果中，钻、磨、去毛刺这三道工序的设备排列相对整体集中（如图8所示），使这一区域的物流方向更加一致，有利于减少物流路径交叉，从该角度出发可以选择此方案作为最终的布局优化方案。目标函数值优化曲线如图9所示,原始布局目标函数值为101 327，在前5 次迭代中结果迅速收敛，优化效果显著。当迭代20次时，目标函数已经基本稳定。因此在不同的场合下，可以根据实际需求在最优逼近程度与求解速度之间做权衡，在获得满意解的前提下选择合适的迭代次数。

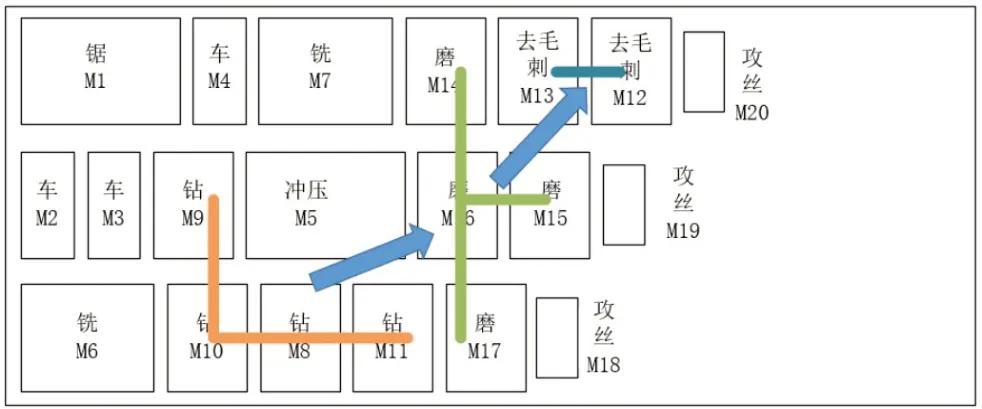
图8 最终布局优化方案

6 结语

本文采用混流生产调度与设施布局规划相结合的方式，提出了一种对车间设施布局及生产调度方案进行相互迭代优化的方法，取代了传统的设施布局与生产调度分离的规划流程，并通过数学模型的建立及仿真，验证了该方案的可行性，同时通过设置路径系数减少了物流路径出现逆向和交叉，降低了物流成本，具有一定的实用性。本文的研究成果在一定程度上弥补了可重构混流生产线使用传统布局规划方法时无法获得并行设备准确物流量的缺陷，为可重构制造系统周期化重置提供了有效的解决办法。

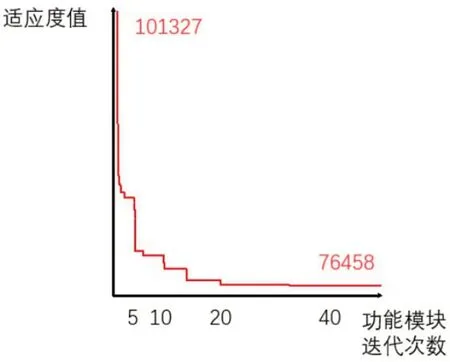
图9 目标函数值优化曲线