基于关联规则与聚类分析的储位分配问题研究

朱铖程，吴兆东，张建东

（1.中国人民解放军92678部队，天津 300042；2.陆军军事交通学院 学员五大队研究生队，天津 300161）

1 引言

为了提高仓库的作业效率，研究人员从仓库设施布局、储位分配、订单分批、执行单元自动化等多个方面入手，分析研究策略并进行优化升级。其中，储位分配问题（Storage Location Assignment Problem,SLAP）主要服务于战略运营层面，在布局、设备确定的条件下，储位分配策略直接影响仓库作业效率。

储位分配问题是将货架的每个储位分配给对应的货物，以达到某种效果最佳，例如方便拣选、方便盘点、出库速度快等。随着物流行业的发展，储位分配问题的研究逐渐成为热点。在上世纪60-80年代，研究人员提出了众多储位分配策略，例如随机存储策略[1]、定位存储策略[2]、分类存储策略[3]等。Heskett[4]在上世纪60年代率先提出了基于货物周转率COI系数的储位分配策略，并证明了在物资完全不相关的前提下，该策略最接近最优解。Hausman[5]等针对自动仓储系统，分别对随机存储策略、基于物资分类的存储策略以及基于周转率的存储策略进行了对比分析，并且发现基于周转率的存储策略可以有效地减少作业中的行走距离。Rosenblatt[6]基于物资品类出库量提出了分类定位存储策略，并发现在品类增加时，可有效缩短物资出库时的行走距离。

储位分配问题被证明是NP难题，早期的研究考虑的条件都较为单一。近年来，随着物流技术和管理作业模式以及计算机技术的发展，储位分配越来越考虑多方面的因素，例如物资之间的关联性、物资自身属性、仓库货架特点等。Rosenwein[7]考虑不同物资之间的需求相关度，建立P-中值二进制优化模型对物料进行聚类，在此基础上进行储位分配。Jewkerse[8]在分区拣选策略基于人工拣选条件时，运用动态规划算法对货位分配与均衡作业量进行了研究，并通过实验验证该方法的有效性。Quintanilla[9]等应用启发式算法，以最大化空间利用率为目标，研究了随机存储策略下半自动仓库的储位分配问题。Yang[10]等在基于COI系数的储位分配理论基础上，结合主成分分析，将待分配的物资进行分类分级，通过计算比较各级物资的COI 系数来确定储位。Xie[11-12]等从商品的尺寸角度出发，建立了具有分组约束的双层规划数学模型，求解得到分组约束条件下的储位分配。赵士博[13]在设计储位优化模型时，应用聚类分析与关联规则，挖掘物资之间的相关性，并将此与物资和仓库其他信息结合起来考虑。

与以往储位分配问题研究侧重于物资本身的属性不同，本文提出的模型侧重于优化仓库对订单的反应敏捷程度，即缩短每一笔订单的出库时间，同时，针对以往研究中的数量关联分析不足，本文在物资关联分析的基础上，考虑了数量上的关联分析。重点针对传统窄巷道立体库的储位分配问题，结合仓储作业的实际情况和储位分配原则，给出窄巷道立体库储位分配问题的规范化描述，建立了基于关联规则分析和聚类分析的储位分配模型，通过求解模型给出了储位分配策略。

2 模型建立

2.1 储位分配问题描述

储位分配是根据仓库的性质、物资的属性等要素，确定各类物资的摆放位置，这是进行仓库一系列作业的前提。就窄巷道立体库而言，对储位分配的研究是指通过合理的储位分配，直接减少工作人员在进行存、取、盘点等作业的行走距离，从而提高作业效率。当前，基于物资COI的储位分配策略[4]可以有效地提高仓库整体的作业效率，而这种储位分配策略仅仅针对一种物资而言，其缺陷在于对于某一个订单而言，如果需要多种物资，这些物资可能相互关联但是被放置在距离较远的位置，会使仓库处理该订单的速度降低。

不管物资如何放置，从储位的角度来看，储位的价值是永远不变的，若以到I/O 口的距离为衡量指标，对于窄巷道立体库而言，其储位的价值可近似看成是沿着半径R的方向下降，即越靠近I/O位置的储位价值越高，如图1所示。通过借鉴现有的储位分配策略，分析仓库出库订单的特点，侧重从物资之间的相关性、物资的需求量、物资的需求频率，结合仓库作业的基本原则，以最大化储位价值为目标，建立储位分配的数学模型。

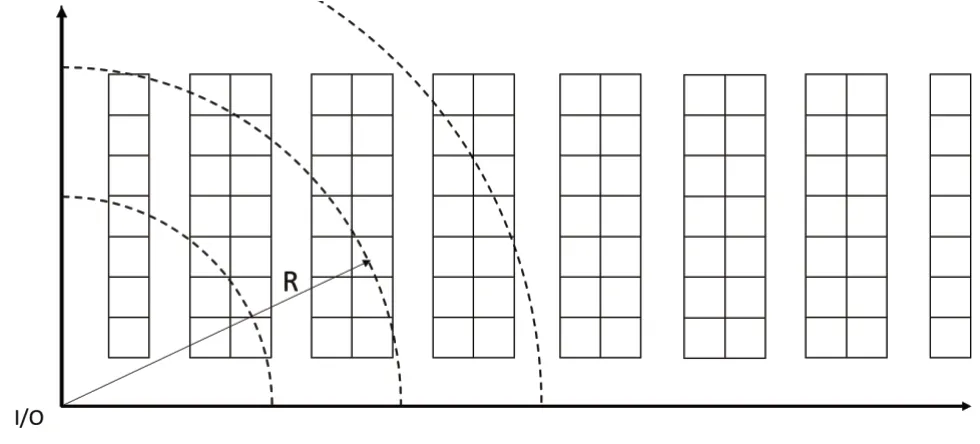
图1 储位价值示意图

储位分配问题的分析流程如图2所示。

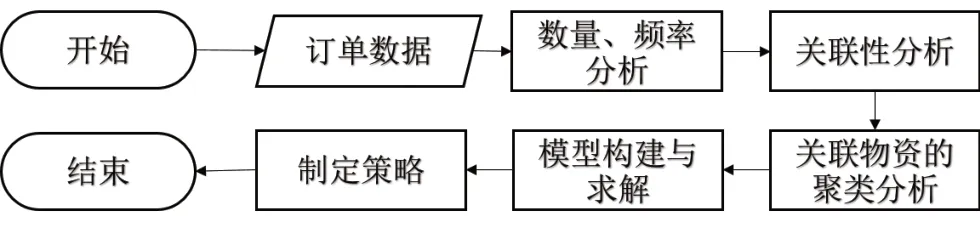
图2 储位分配问题分析流程

2.2 储位分配的基本原则

就储位分配问题而言，核心是提高运行效率和可靠性，需要遵循以下几点原则：

（1）周转率原则。周转率高意味着货物出入库的数量较多，通常需要将其安排在距离仓库I/O口较近的区域。

（2）集中存放原则。对于同一品类的物资而言，要求储位区域尽量集中。窄巷道立体库的出入库作业、盘点作业、维护保养作业等通常由人工完成，因此，为了便于员工执行作业，对于同一品类的物资，要求集中存放。

（3）区域均衡原则[14]。物资集中存放方便人工识别和作业，但是过程中可能会在某一时间段内，某一类物资或几种物资因存取频繁导致库内交通拥堵。因此，在考虑集中存放的同时，需要考虑作业区域分布均衡。

（4）均匀承载原则。通常，货物之间重量、规格区别较大，在进行货位分配时，需要考虑货架整体承载力和受力均匀，意味着储位上的物资需要满足上轻下重的要求。

（5）物资关联原则。储位分配要求能够对出库订单作出迅速的反应，这就要求工作人员能够在最短的时间内执行完作业。一个订单中可能含有多种物资，若将相关程度较大的物资就近存储能够减少中间辗转的距离。

2.3 储位分配模型的基本假设

根据储位分配的部分规则、仓库运营情况与实际作业情况，本文模型基于的假设如下：

（1）不同种类物资的包装规格尺寸标准统一；

（2）一个货位只存放一种货物；

（3）采用分类分区存储策略，即同类物资在货位分布上集中存放；

（4）物资到I/O的距离为这些集中存放物资的质心；

（5）叉车与其货叉在窄巷道立体库中匀速运动，忽略加速减速过程；

（6）忽略叉车转向的影响；

（7）叉车一次能够叉取的某种货物的数量，称为该类货物的一个单位数量；

（8）仓库在一定时间区间内的订单具有规律性，且在该阶段内与时间无关。

2.4 符号说明

符号说明见表1。

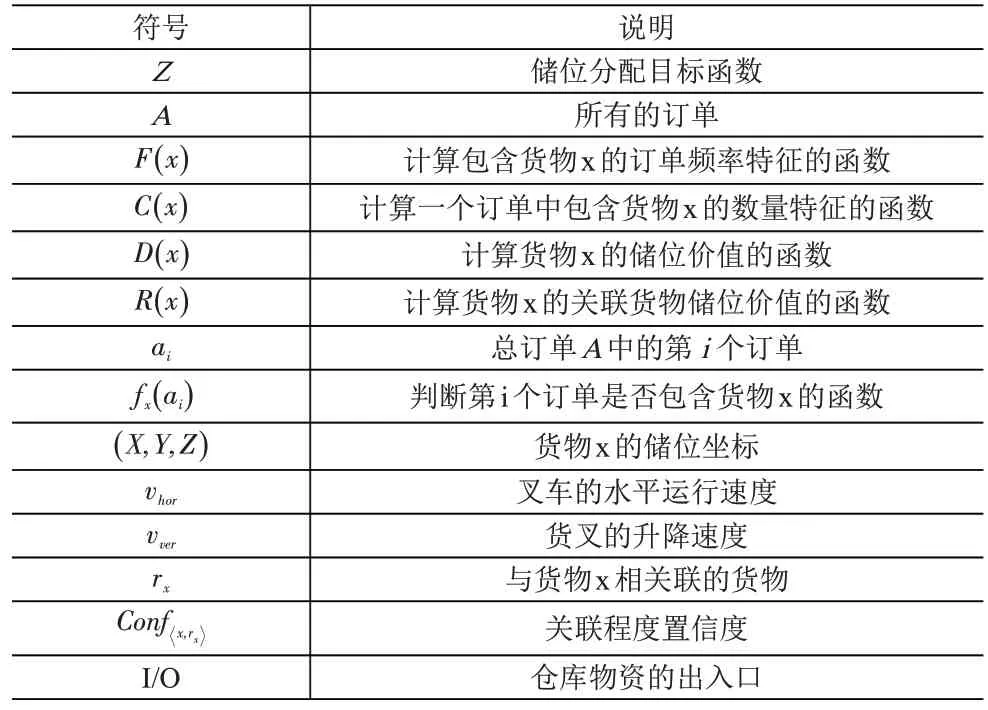
表1 符号说明

2.5 模型构建

基于上述储位分配问题描述、原则与假设，优化的目标为最大化储位价值，构建储位分配问题的目标函数如下：

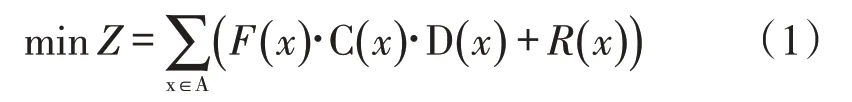
式（1）主要包含两个部分，第一部分表示货物x自身的储位价值，第二部分表示关联物资的储位价值。其中，F(x)表示订单中货物x 出现频率的特征函数，C(x)表示订单中货物x出现数量的特征函数，D(x)表示货物x储位价值的特征函数，具体表示为储位到出口的距离，R(x)表示货物x 的关联物资的储位价值。就订单而言，最大化储位的价值，即要求该订单中涉及的物资的拣货距离总和最短。

F(x)是对订单中货物x 出现的频率进行统计，其计算公式如下：

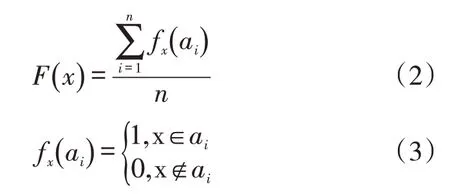
C(x)是对订单中货物x 的数量统计特征，由于是一维数据，数据量庞大，数据中噪音的影响可以忽略，这里采用基础的数学统计分析方法。

F(x)表示订单含有货物x 的概率，C(x)表示订单中含有货物x 的数量，则F(x)·C(x)可以理解为一个订单中含有货物x的期望值。

D(x)不仅与货位的位置(X,Y,Z)有关，也与叉车的水平运行速度vhor和货叉的升降速度vver有关，通过权值变换，其计算公式如下：

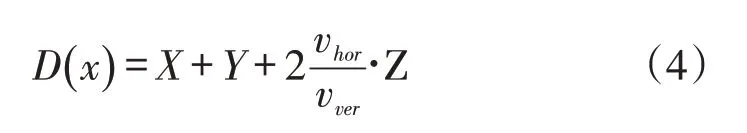
R(x)是指与货物x关联程度较高的物资的储位价值。同样，它涉及到关联物资的数量期望值与关联物资的储位位置，因此表达式如下：

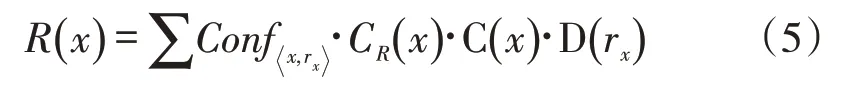
其中，CR(x)是反映关联货物之间数量关系的系数，其计算可以分为2 个步骤，首先是根据关联规则得到与其关联程度较高的货物为关联程度的置信度；第二步是将订单数据简化为ai={x=c1,rx=c2} ，将其看为二维的坐标数据，再通过二维数据的K-means 聚类分析货物之间数量上的关联特征。D(rx)的计算方式同式（4）。

3 模型求解

该模型求解涉及3 个步骤，第一个步骤是利用Apriori 关联规则算法得到物资种类关联关系，第二步是通过DBSCAN 密度聚类，得到不同物资之间的数量关系，第三步是通过回溯法，搜索解空间得到相对最优解。

3.1 Apriori关联规则算法[15]

关联规则分析是从大量数据中挖掘出事物之间的关联关系，其基本的表达方式是A⇒B，意思是某一条数据包含A，则很有可能同时会包含B。在本文的研究中，关联规则主要用于分析货物之间的关联程度。

在关联规则分析中，支持度和置信度是用来量化关联分析的基本指标，以关联规则A⇒B为例，支持度是指待挖掘的数据集合中同时包含A 与B 的样本个数占所有样本数量的百分比；规则A⇒B的置信度是指同时包含A 与B 的样本个数占只包含A 的样本数量的百分比。计算公式如下：

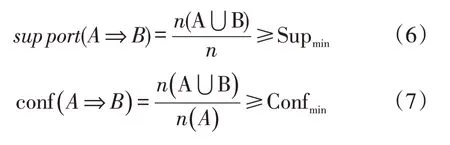
关联规则分析主要分为2个步骤，挖掘频繁项集和挖掘关联规则。这里基于Apriori算法来进行关联规则的挖掘。

算法的计算步骤如下：

集合Lk中每一个项集含有k项，项集的个数＞0：计算每个项集是否满足式（6），若满足，保留频繁项集，由新保留的频繁项集构建k+1 项组成的集合Lk+1，并重复操作。

算法第二个步骤的伪代码描述如下：

对于频繁项集中每一个项：

生成关联规则列表，从右部只包含1个项开始；

计算关联规则的置信度是否满足式（7）；

重复上述操作。

在该模型中，计算流程如图3所示。

图3 模型计算流程

3.2 DBSCAN密度聚类算法

密度聚类算法是基于样本分布的紧密程度对样本进行分类，相比较于K-means 聚类分析方法，密度聚类可以较好地处理数据噪声的影响[16]。其核心思想就是通过发现密度较高的点，将相邻的高密度的点连成片，从而生成各种簇。

在密度聚类中，将点主要分为3类：核心点、边界点和噪音点。核心点是指在该点半径为er范围内的点的个数大于等于Ptmin的点。边界点是指不满足核心点的条件，但是在核心点的半径范围内的点。噪音点是不满足上述两者的点。

DBSCAN算法的伪代码描述如下：

定植：定植前需进行土壤消毒处理。每亩施腐熟有机肥（猪粪、鸡鸭粪肥）2500kg、复合肥25kg，翻耕入土，整平后筑畦宽60～65cm、沟宽30cm、沟深20～25cm。草莓花芽分化时为最佳定植期，幼苗带土随起随栽，每畦种2行，株距17～18cm，每亩栽7000株。

将所有的点按要求划分为核心点、边界点、噪音点；

删除噪声点；

距离小于等于er的核心点用边连接；

每组连通的核心点组成一个簇；

边界点指派到关联的核心点的簇中。

本文中应用聚类分析，主要是为了分析订单关联规则中涉及两种货物之间的数量关系特征，属于二维密度聚类。其计算流程如图4所示。

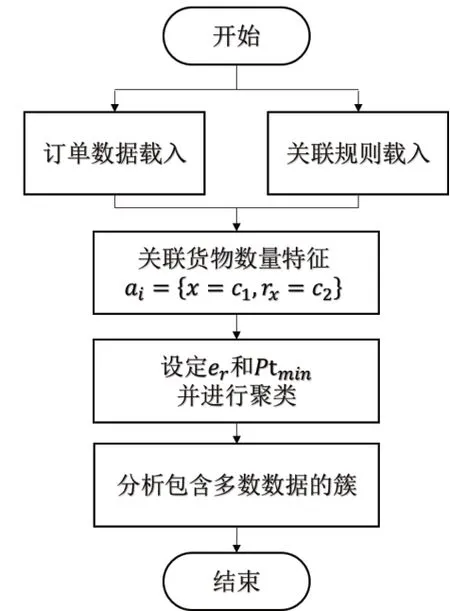
图4 密度聚类计算流程

3.3 回溯法求解

在3.1 节和3.2 节算法分析的基础上，可以确定优化目标式（1）中除货物储位位置以外的参数。这样，模型就可以看做是一个TSP 问题，这类问题也是NP完全问题。有i种货物，每种货物的数量为wi，按照距离I/O 口的距离，根据不同类别的物资进行排列，分配储位，使得储位价值最高，储位分配方案如图5所示。

图5中，将距离远近近似看成扇形区域，图中的储位分配方案可以描述成，I/O的第一个扇形区域储存物资A，下一个环形区域储存B，剩余区域储存C。通常求解该问题的方法有回溯法[17]、分支定界法[18]以及一系列启发式算法。本文采用回溯法对该问题进行求解。回溯法是一种以深度优先的搜索算法，以3种货物A、B、C为例，可以建立二叉树图，如图6所示。

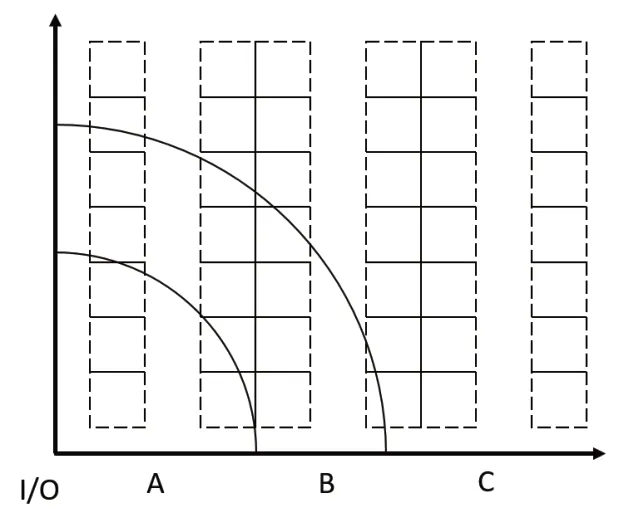
图5 储位分配方案示意图

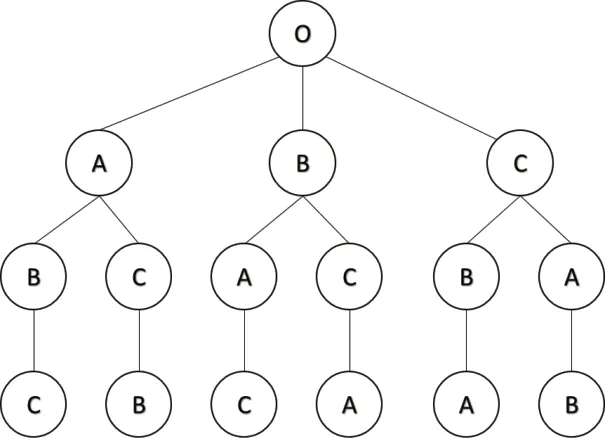
图6 二叉树图

图6展示了储位分配解的空间树，通过搜索空间树，并利用剪枝函数判断节点是否可行来寻找最优解。

4 案例分析

4.1 模型计算

以某电商仓库的出库订单记录为例，应用本文模型进行储位分配方案的规划。这里获取了该电商仓库2017年上半年的出库记录4 322 条。该仓库共有储位 500 个，10 列，5 层，每列有 10 个货位，主要负责6大类物资的发货任务，即饮品类、速食类、卫生用品类、玩具类、文具类以及宠物用品类，其订单数据见表2。

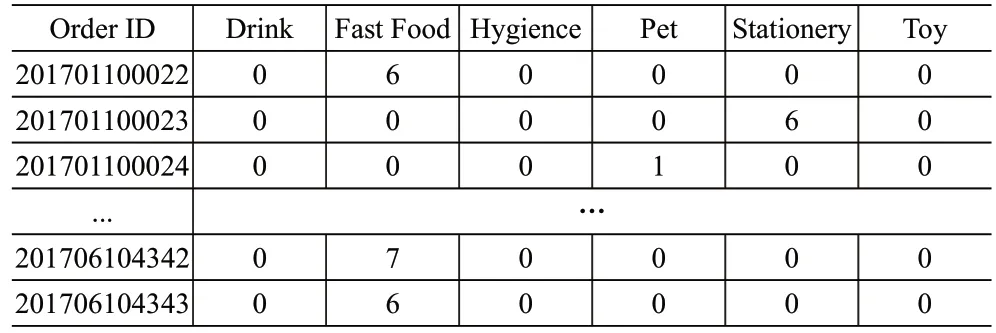
表2 订单详情

第一步，通过Matlab 编程实现Aprorio 算法对这些订单数据进行关联规则分析，设定支持度为0.2，最小置信度为0.45，可以得到关联规则30条左右，见表3。

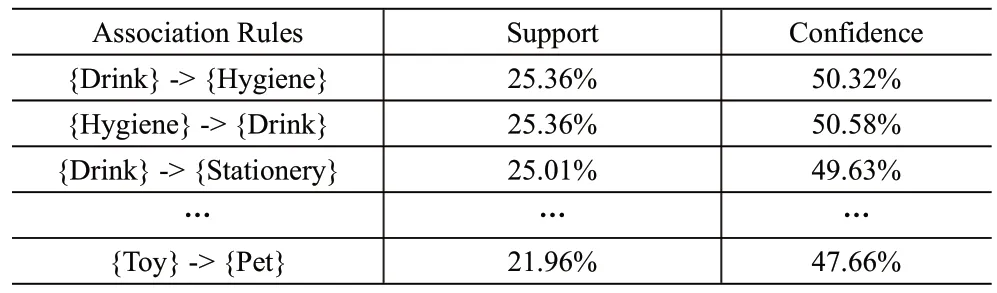
表3 生成关联规则示例

通过关联规则分析可以确定式（5）中与货物x关联程度较高的货物rx以及置信度矩阵，见表4。

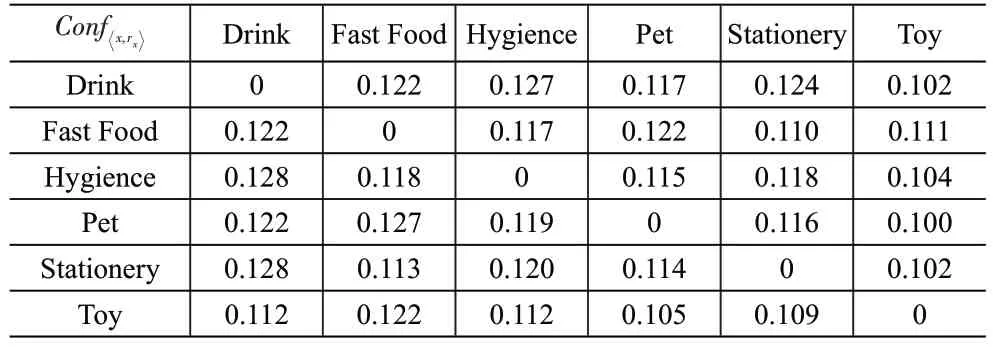
表4 置信度矩阵

第二步，数量特征分析。通过数学统计的方法，分析每一类货物出库的数量特征。针对关联货物的数量关系，通过二维的K-mean 聚类算法进行分析。首先，每一类物资的数量特征如图7所示。

这几类货物出库量的数学统计特征见表5。

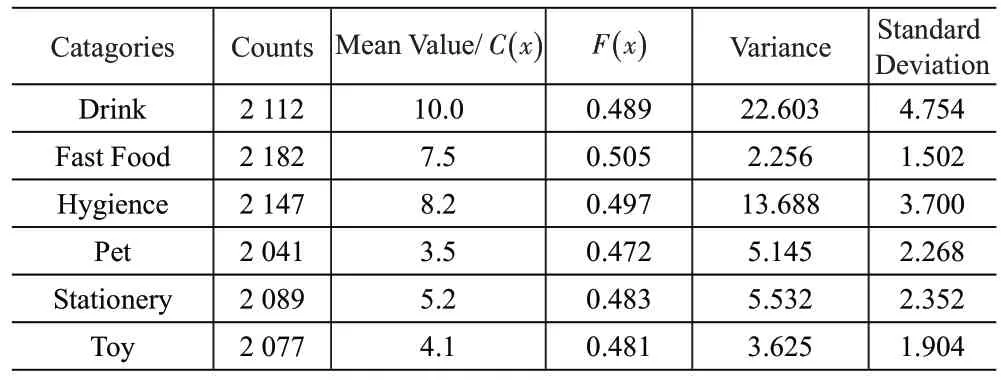
表5 物资数学统计特征

Counts 是指某类物资数量非零的订单总数。通过加权平均，就可以得到每类物资的出库平均值，该值可以认为是一个订单中包含该类货物的数量。

由关联规则和订单数据，可以提取两种货物同时出现在一个订单上的数量关系。将两种货物视为两个维度，货物的数量视为在该维度上的取值，通过MATLAB 编写的DBSCAN 密度聚类算法程序，以Drink 货物为例，得到Drink 与其他货物的数量聚类图像，如图8所示。

以聚类中占数量最多的一类的质心作为关联货物之间的数量关系，可以得到关联货物的数量关系系数矩阵，见表6。

第三步，利用回溯法搜索最优解。经过前两步的计算，除位置信息以外的其他参数均已确定，剩下的就是确认各类物资在储位分配上的位置关系，即对靠近I/O的程度做一个排序。

该电商仓库遵循集中存放原则，同时储位较为充足，采用了划区域分类存储物资策略。对D(x)的计算，可以简化成离散变量表示。由于上述只有6种物资，这里通过{1,2,3,4,5,6} 等差数列形容各区域的储位价值。

通过Matlab 编写回溯算法，以式（1）为优化目标，计算求解得到最终的储位分配距离I/O由近及远分别是{Drink、Fast Food、Hygience、Stationery、Toy、Pet}。

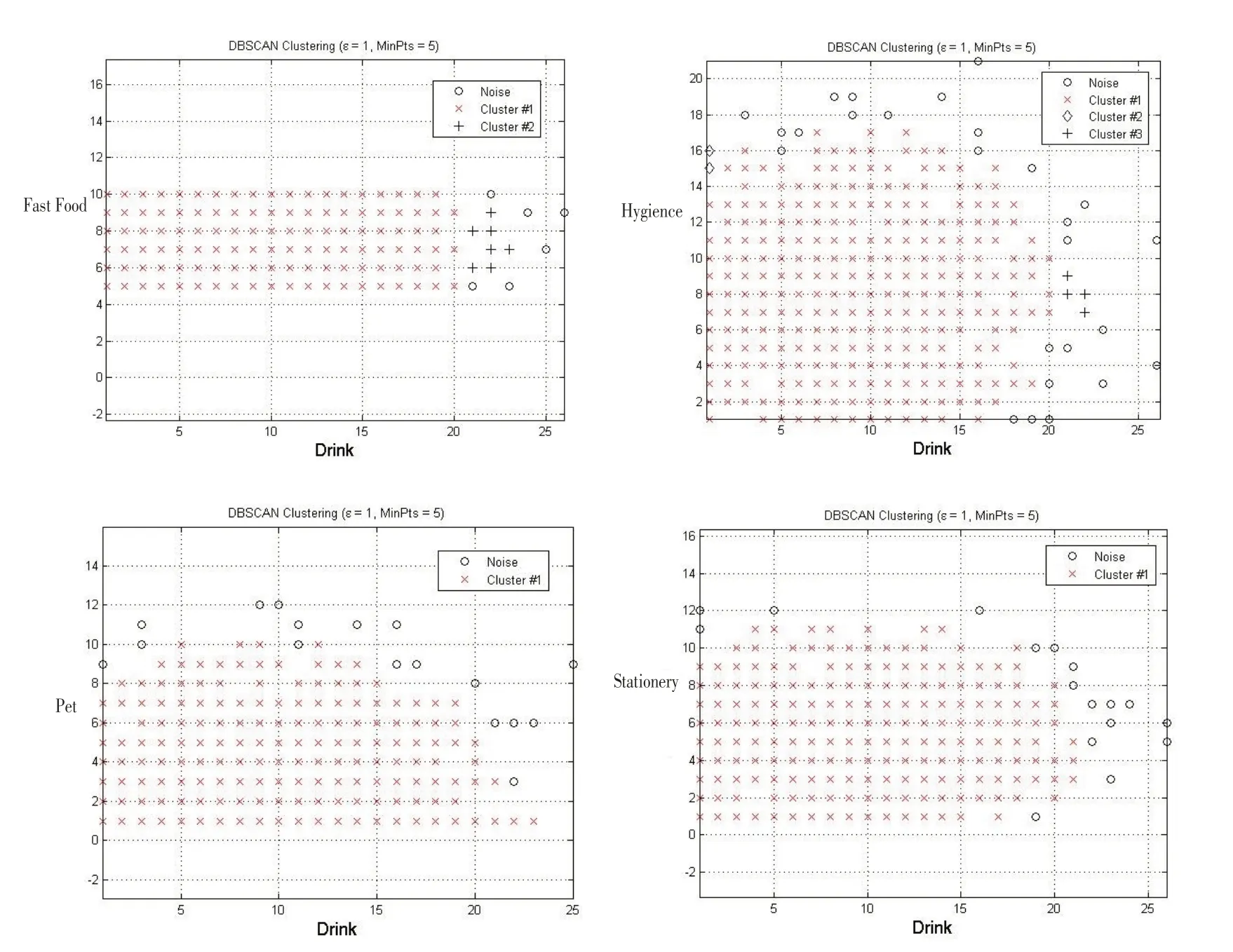
图8 物资-频率关联图

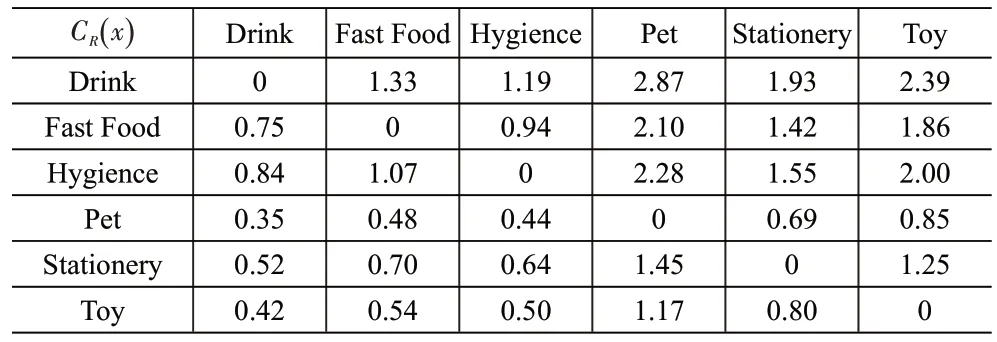
表6 数量关系系数矩阵

4.2 策略对比

若单纯基于物料COI进行储位分配，则储位分配中，距离I/O 口的物资顺序应是{Drink、Hygience、 Fast Food、Stationery、Toy、 Pet}。 取2017年下半年7月份500 个订单数据测试，以{1,2,3,4,5,6} 表示距离I/O 相对距离的绝对值，对比4.1 节最后的方案，结果见图9与表7。

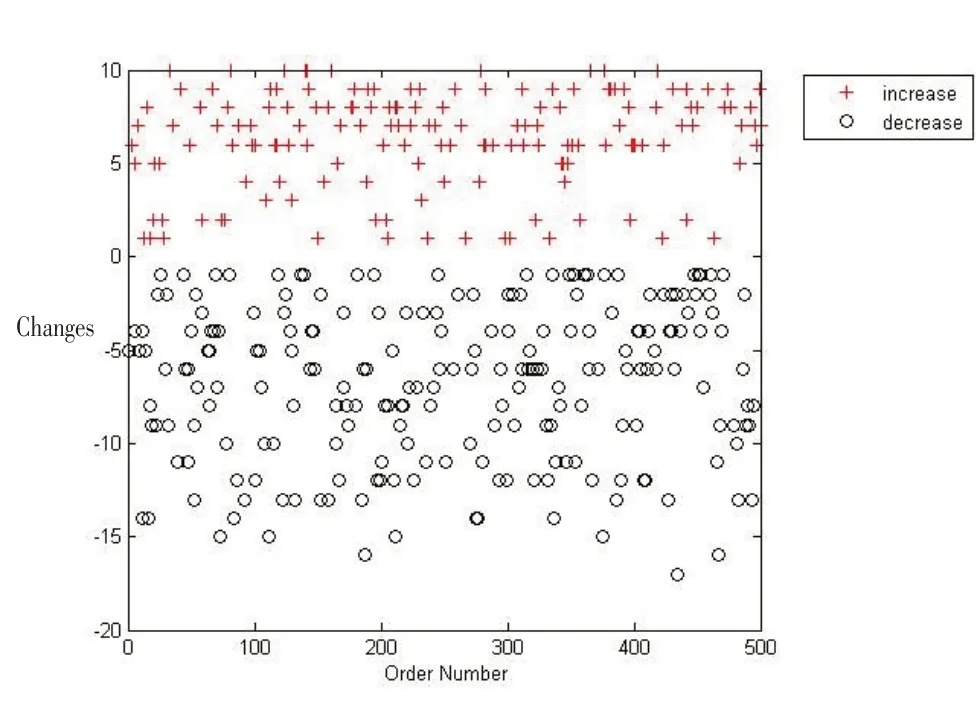
图9 本文储位分配策略与基于物料COI的储位分配策略对比变化示意图

纵轴表示增加的距离值，“+”号表示因策略变更增加货物出库距离的订单，数量为152个，“o”表示距离减少的订单，数量为213 个，总共减少的距离为489。可以发现，该策略从总体上优化了出库的效率。

5 研究结论与展望

本文主要研究了传统窄巷道立体库的储位分配问题。首先，根据窄巷道立体库的实际背景，给出了本文所研究的储位分配问题的规范描述。接着，从仓库出库订单角度出发，以缩短订单货物的出库距离为优化目标，结合储位分配的一些原则，建立基于关联规则与聚类分析的储位分配模型。在模型中，一些基本参数通过统计数学方法得到，与不同物资关联程度相关的参数通过Apriori关联规则算法求解得到，与货物之间数量关系相关的参数通过聚类分析得到。应用回溯法求解整个模型。

将模型应用于某一电商仓库，将电商仓库提供的数据集划分为训练集与测试集，通过训练集得到了新的储位分配策略，并应用测试集对比基于COI的分配策略。计算过程表明，通过关联分析发现，在订单中存在大量的物资关联信息，这些关联信息反映了同一个订单包含不同类的物资在统计上的关系。同时，通过对这些关联物资进行聚类分析，可以挖掘出这些不同种类的物资在同一订单中的数量关系。研究求解模型得到相应的储位分配策略发现，在局部上，模型对不同的订单有的产生了正面的优化效果，缩短了出库距离，有的产生了负面效应。但是，从优化的订单数量与优化的幅度来看，优化效果要高于产生的负面效应，因此可以说基于本文模型提出的策略在整体上优化了订单出库距离。

本文的研究是建立在场景条件相对理想的条件下，例如物资包装规格尺寸统一、仓库布局单一、叉车速度运行稳定、订单数据具有代表性等，与实际仓库的作业环境有所出入，这些也为下一步的研究提供了思路。下一步将重点研究以下几个方面：（1）物资包装规格尺寸不统一的影响；（2）不同时间区段订单数据的变化趋势对储位策略的影响；（3）不同仓库布局的影响。