基于PSO算法的应急物流车辆调度

袁世军，梁瑞伟

（湖南现代物流职业技术学院，湖南 长沙 410131）

1 引言

应急物流的主要目标是应对严重自然灾害、突发性公共卫生事件、公共安全事件及军事冲突等突发事件而对物资、人员和资金等提供物流保障，但如何使应急物流在满足需求的前提下做到成本最低，一直是物流管理重要的研究领域。

本文将PSO（粒子群优化算法）引入应急物流车辆调度问题中，其基本原理是将应急物流中多个供应点与多个需求点作为粒子群中的不同粒子，依靠不同粒子间的相互作用寻找最佳供应点、最优配送车辆以及配送线路在整个寻优空间里的最优位置，也即问题的最优解。在此粒子群中的每一个粒子都将赋予一个适应度值，每个粒子具有2个属性，即速度与位置。算法运行过程中，所有粒子趋向当前时刻的最优粒子的位置，并试图在可能空间中搜索全局最优解。本文对应急物流车辆调度问题做了一定的假设，使得问题更加清晰简洁。在假设的基础上构建了改进应急物流车辆调度模型，目标函数为使因物资需求延迟满足而引起的损失最小。

2 问题描述

为了建模方便，将应急物流车辆调度问题抽象为：在n个应急货物供应点s1,s2,...,sn，储备了p种应急货物a1,a2,...,ap，其单位货物的重量为wa，单位货物体积为va，在t时间范围内，应急货物供应点s货物a的供给量为Xtsa；在所有供应点S，可使用的车辆总数为q，车辆表示为l1,l2,...,lq，车辆的最大载重量为Kl，最大容积为Vl，负责对m个物资需求点d1,d2,...,dn运输应急货物。在t时段内，需求点d对物品a的需求量为Wtda。

将整个运输周期T划分成N个时段，表示为t1,t2,...,tN，则在t时段需求点d对物品a未被满足的数量为disstda，因此而引起的损失为Pa·disstda，Pa表示单位a物品未满足而造成的损失。若某需求点对某物品在该时段内未得到满足而在往后的时段内得到满足，则之前因未满足引起的损失可以相应的部分抵消，如需求点d对a物品在t时段未被满足而在t+j时段内满足的数量comt,t+j,da，则挽救的损失为(Pa-kj)×comt,t+j,da，(Pa-kj)表示单位a物品延后j时段挽救的损失与Pa之间的线性关系。此外，为了将整个运输周期的损失降到最低，应急货物允许提前运送到需求点。

本文研究的目的是设计针对应急货物调配的最佳车辆调度方案，通过调度各应急物流货运车辆共同参与且依次完成其运输任务，使得应急货物需求得到满足且损失最小。

3 模型建立的假设

根据应急物流的特点，便于模型建立，特作以下假设：

（1）假设各应急中心在整个运输周期内对物品的需求量服从正态分布N(μda，σda)，其中μda表示需求点d对物品a的平均周期，σda表示需求点d对物品a时间的方差，则第t时段需求点d对物品a的需求量为（T0为每个时段长度）：

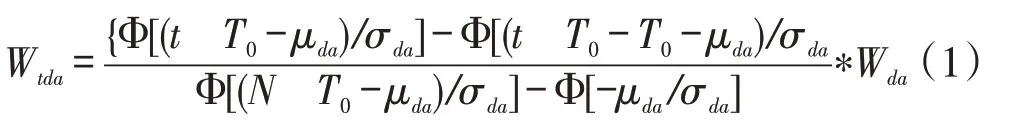
（2）假设单位物品a在t时段未被满足而在t+j时段内满足的损失减少量P减少满足P减少=Pa-kj的一元线性关系（也可假设为满足其他关系，本文仅以满足一元线性关系进行研究），k为系数，且k≤Pa/N。

（3）车辆完成一次运输任务后可以随机选择运输网络中任一个供应点作为下一个任务的起始点而不是只能回到原出发点。

（4）在应急事件发生的情况下，受灾点对各种应急货物需求量非常大，因此只考虑满载运输方式。

（5）运输时间都以时段数来衡量，不足1时段的以1时段计算。

（6）模型中的参数：

T：整个运输周期；

N：计划期的总时段数；

L：车辆集合；

D：需求点集合；

S：供应点集合；

A：应急货物种类集合；

Kl：车辆l的最大载重；

Cla：车辆l运输a物品的最大数量Cla=min(Kl/wa，Vl/va)；

Pa：单位a物品未满足的惩罚系数；

Zlks：车辆l执行第k个任务所在的供应点为s；

Zlkd：车辆l执行第k个任务所在的需求点为d；

Zlka：车辆l执行第k个任务所运输的物品为a；

Wtda：t时段需求点d对a物品的需求量；

Mtda：t时段需求点d对a物品的满足量；

Xtsa：t时段从供应点s运出a物品的数量；

Ytda：t时段运输到需求点d的a物品的数量；

SYtda：t时段末需求点d物品a的剩余量；

SYtsa：t时段末需求点s物品a的剩余量；

disstda：t时段需求点d对a物品未满足的数量；

comt,t+j,da：需求点d对a物品在t时段未被满足而在t+j时段内满足的数量。

4 模型建立

基于PSO应急物流车辆调度模型的目标：在整个时间范围内，所有应急物流需求节点、所有应急货物虽因延迟满足但其引起的损失从系统的角度来看是最小的。

式（2）表示模型的目标函数，其中第一项表示应急点需求没有得到满足产生的损失，第二项表示在延迟满足的情况下，其损失的减少量。

式（3）表示在t时段需求点d对a物品未满足的数量等于该时段该需求点对该物品的需求量减去满足量。

式（4）表示t时段应急货物需求点d对a物品的满足量的关系。当t-1时段末应急货物需求点d应急物品a的库存与t时段运输到该点d的a物品的数量之和小于t时段需求点d对a物品的需求量时，Mtda=SYt-1,da+Ytda，否则，当t-1时段末需求点d物品a的剩余量与t时段运输到需求点d的a物品的数量之和大于t时段需求点d对a物品的需求量时，Mtda=Wtda。

式（5）表示t时段末需求点s物品a的剩余量的关系，当SYt-1,da＞0，即上一个时段末的剩余量大于0时，则SYtda=max(SYt-1,da+Ytda-Wtda,0)，即该时段末的剩余量等于上一时段末的剩余量加上该时段运送到的物品量减去该时段的需求量与0的最大值；当SYt-1,da=0时，则，即该时段末的剩余量等于该时段运送到的物品量减去该时段的需求量减去1到t-1时段的未满足量再加上1到t-2时段的未被满足需求在1到t-1时段得到的补充量与0的最大值。

式（6）表示需求点d对a物品在t时段未被满足而在t+j时段内满足的数量的关系，当=0时，即t时段需求点d对a物品未满足的数量减去t时段的需求在1到t+j-1时段内得到满足的数量之差等于0时，说明此时段的需求全部已满足，所以comt,t+j,da=0；当时，即此时段仍有未满足量，则即t时段未被满足而在t+j时段内满足的数量等于t+j时段到达的运输量减去1到t-1时段在t+j时段得到的满足量，与t时段的未满足量减去t时段在1到t+j-1时段内得到的满足量中的最小值，这里假定时段靠前的未被满足量优先得到补充。

式（7）表示t时段末需求点s物品a的剩余量等于上一个时段末的剩余量减去该时段从该供应点运送出去的量。

式（8）表示车辆l从供应点s运出a物品的数量等于车辆l运输a物品的最大数量，且不得大于车辆l的最大载重。

式（9）表示Wtda，Mtda，disstda，comt,t+j,da，SYtda，SYtsa和Zlks，Zlkd，Zlka的取值范围。

式（10）表示车辆执行每个运输任务都只能有一个供应点、一个需求点和运输一种物品。

式（11）表示Zlks，Zlkd，Zlka的取值范围。

在整个运输计划中，各应急中心可能随时提出新的需求，物资储备中心也可能从外界接收新的物品数量以增加对应急中心的供应量，也可能征集到新的车辆或民间组织或个人的车辆加入进来，对于这些实时信息的处理方法如下：对于新加入运输计划的供应量，则此时段的供应量等于上一时段该供应点的剩余量加上新加入的供应量；对于新加入运输计划的需求量，则此时段需求点的需求量等于原有的需求量加上新加入的需求量再减去已满足的需求量；对于新加入运输计划的车辆，在保持原有车辆的运输任务不变的情况下，对新加入的车辆安排新的运输任务。通过对系统输入参数的更新，运用模型进行求解，即可得到系统更新后的输出参数。

5 求解应急物流车辆调度模型

5.1 粒子编码方式

为了求解应急物流车辆调度问题，本文设计了一种适合求解本文模型的编码方式，即符号编码。符号集可以由字母组成，也可以由数字组成，也可以是由字母或数字混合组成的代码表，如{A1,A2,A3,……}。具体的粒子编码步骤如下：

（1）将供应点表示为{S1,S2,...,Sn}，需求点表示为{D1,D2,...,Dn}，物品表示为{A1,A2,...,An}。

（2）每一个符号集代表一个运输任务，如符号集{S1,A2,D3}表示该车辆从供应点S1运输物品A2到需求点D3，车辆的所有符号集按照任务的完成顺序依次排列组成，如{S1,A2,D3}{S3,A5,D1}{S2,A3,D1}表示该车辆从供应点S1运输物品A2到需求点D3，再到供应点S3运输物品A5到需求点D1，再到供应点S2运输物品A3到需求点D1。

（3）所有车辆的第一个任务集按车辆的顺序排列组成第一任务集，然后依次类推。最后得到所有车辆所有任务集，并按照第几任务集按顺序排列。

（4）每辆车完成的最大任务数由每种物品的库存量和整个运输周期确定。如对于某种物品，将涉及到这种物品的所有任务的装载量进行累加，如累加第k个任务时的和大于此种物品的供给量，则第k个任务和之后的任务全部赋值为0，即清除这些任务；超过整个运输周期的任务调整也用同样的方法对任务集进行调整，最后得到符合条件的任务集。

5.2 适应值函数

对于车辆调度问题来说，在构造适应值函数时，往往会结合模型中的约束条件来构造，也就是说将在求解中难以处理的约束条件加入到目标函数中共同构造问题的适应值函数，如约束条件不满足，则解空间中无对应解的粒子，则对此解给予一个罚函数，使之被淘汰，从而减少求解时的操作次数，即用下列公式对粒子进行调整：

式中：Z(X)表示原适应值；Z′(X)表示考虑罚函数之后的新适应值；P(X)表示罚函数[8-9]。

本文使用罚函数法对违反约束的情况进行惩罚，使式（7）构成的罚函数成为适应值函数的一部分，构成的适应值函数为：

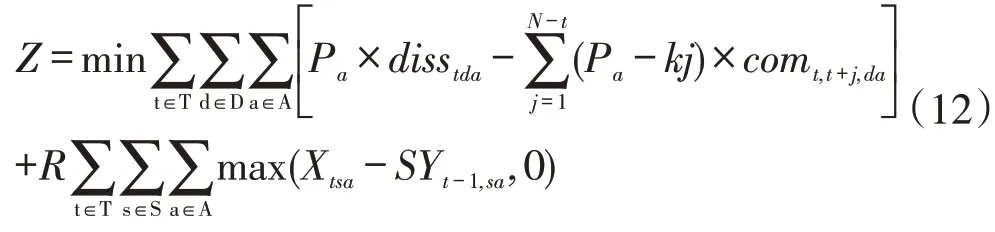
其中，R表示惩罚系数，为了严格满足库存约束条件，R应趋于无穷大，但为了处理方便和计算简单，R一般取一个适当的整数，如R=106。

5.3 数值仿真分析

为了对前面提出的模型和算法的有效性进行验证和分析，本文构造了一个算例。算例如下：在春季的某个上午，某个地区发生了一次突发性地震灾害，应急货物储备中心接到上级命令，需将所需的救援物资在6个小时内运输到各应急中心，在三个地区的某小区、学校和开发区的绿化地、操场和广场分别设立了3个应急中心，应急货物储备中心征集到了10辆车进行帐篷、食品和衣物三种应急货物的配送工作。

整个运输周期为6h，本文将运输周期等分为12个时段，每个时段长为30min。为了简化求解运算过程以及编程的复杂性，这里我们只考虑一个供应点进行供应的情况，假设供应点的现有物品数量在整个周期内不会产生变化，且车辆的规格一致。

5.3.1 基础参数设置。系统输入数据包括各灾区的基本信息、应急货物的储备信息、各应急货物的基本信息、车辆基本信息和应急货物储备中心到各应急中心的最短路径信息。

（1）各灾区的基本信息。各灾区的基本信息见表1，各物品的需求量服从均值为10，方差为12的正态分布N(10,12)。

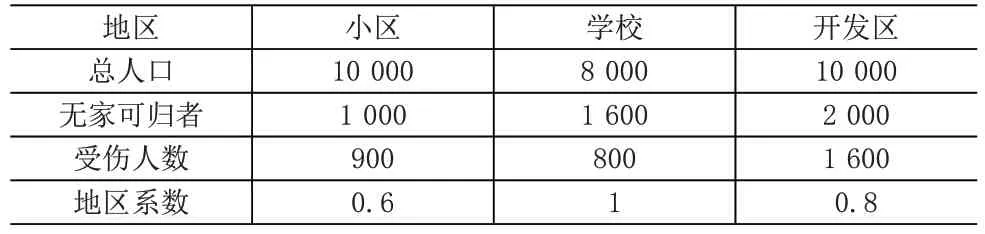
表1 各灾区基本信息

这里取季节系数为0.9，根据前文各物品的需求计算公式可得到各应急中心对各物品的需求量，具体数据见表2。

表2 各应急中心需求量和储备中心的供应量

根据表2、式（1）以及服从正态分布N（10,12），可得出各应急中心各个时段的需求量，具体数据见表3。

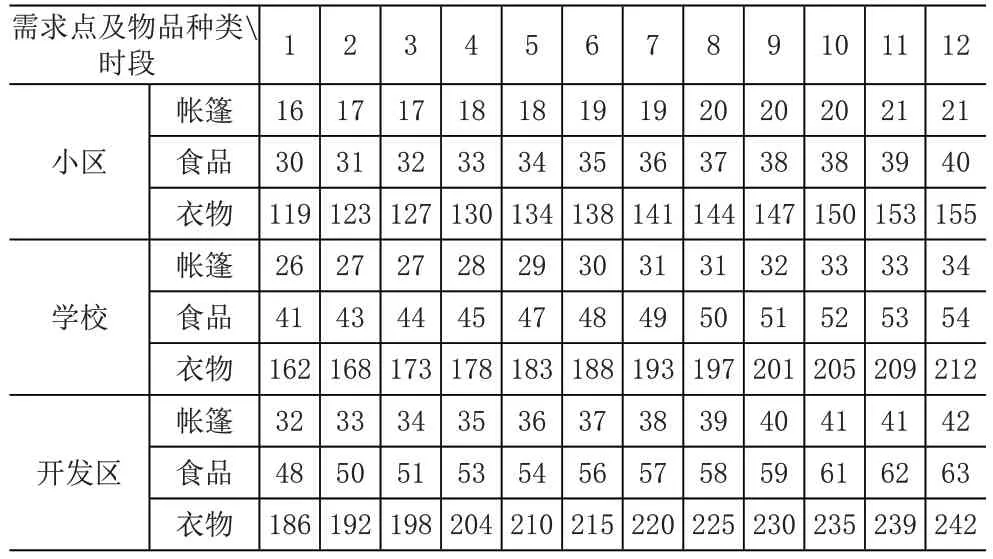
表3 各需求点在各个时段对各种物品的需求量

（2）各应急货物的基本信息。各应急货物的单位重量、体积、惩罚系数等基本信息见表4。

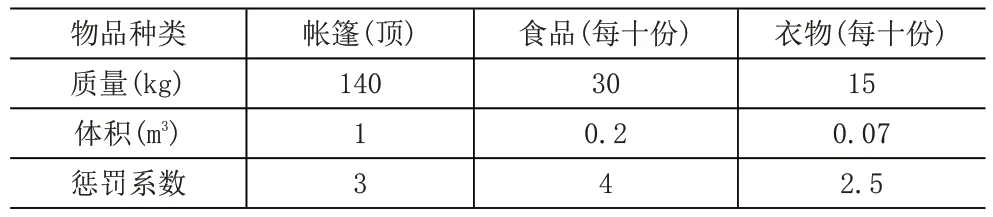
表4 各应急货物的基本信息

（3）车辆基本信息。应急货物储备中心共征集到10辆车辆进行运输，且车辆规格一致，车辆的基本信息见表5。

表5 车辆基本信息

（4）最短路径。应急货物储备中心到各应急中心的最短路径见表6。

表6 储备中心到各应急中心的最短路径（km）

5.3.2 构建模型并求解

（1）目标函数值。根据问题输入、设定的初始参数，在windows XP，内存1G 的电脑环境下进行运算，得到本算例的目标函数值为：Z=4 482.96，趋势图如图1所示。

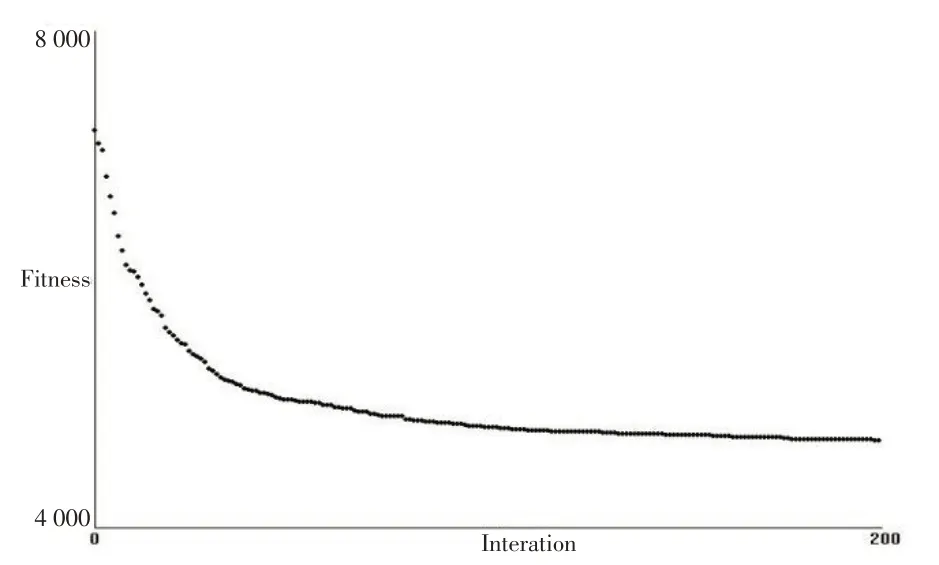
图1 目标函数值曲线图

（2）车辆的运输任务。车辆的运输任务见表7。以应急物流配送车辆2为例，应急物流配送车辆2执行了四个应急配送任务，分别为：从应急物流中心配送衣物到学校，再从储备中心运输食品到小区，再从储备中心运输衣物到开发区，最后再从储备中心运输帐篷到小区。

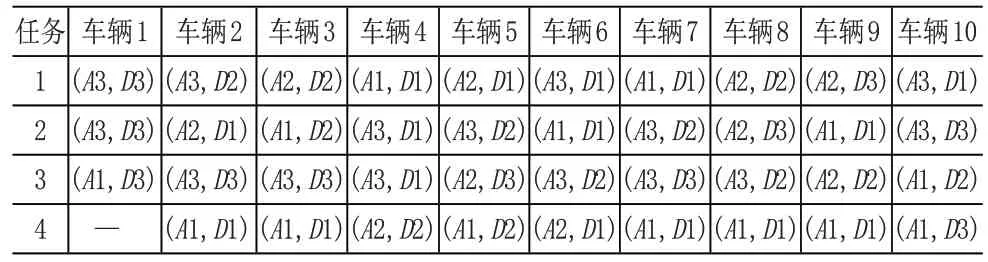
表7 各车辆的运输任务

（3）各应急中心在各时段内得到的应急货物数量（以需求点小区，帐篷为例）见表8。

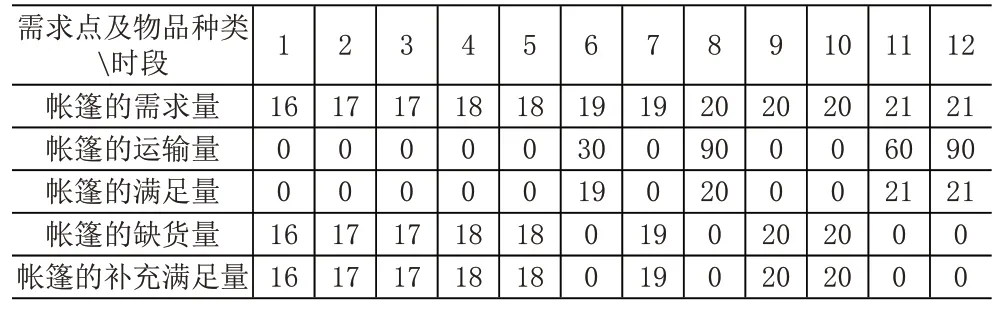
表8 各应急中心在各时段内得到的应急货物数量

6 与其他算法的比较分析

6.1 模型改进前后比较分析

本文所建立的应急物流车辆调度模型是在前人的基础成果上进行改进，为了体现改进后的模型的有效性，对改进前的模型和本文改进后的模型进行对比分析：

改进后模型：

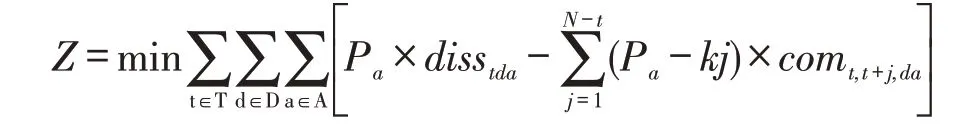
算法参数按照上文最初的参数配置进行实验，以改进前的模型和改进后的模型分别进行运行计算后得到的结果数据见表9，适应值趋势图如图2所示。可以看出，改进后的模型不仅更符合实际情况，而且适应值远小于改进前。

表9 模型改进前后的适应值比较

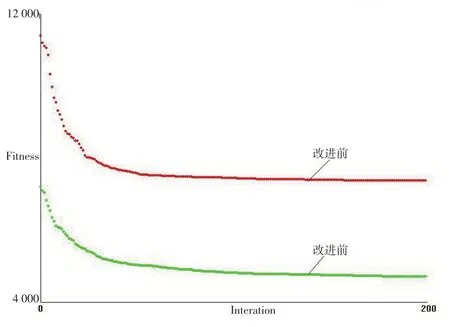
图2 模型改进前后的适应值趋势图

而且，从模型改进前后的车辆任务分析可以看出，模型改进前得出的车辆任务更优先运输衣物，这是因为改进前的模型不考虑延迟满足带来的损失挽回量，而由于衣服的需求量和车辆装载量最大，优先安排更多的车辆运输衣服可以减少整个运输物资未满足带来的损失量。但我们知道，在发生自然灾害的情况下，每种物资的需求量和重要性不一定匹配，也就是说需求量大的物资并不一定重要性就更大，比如药品。所以，模型未改进的实验结果与实际情况是有出入和偏差的，对于实际应用价值不大。

6.2 与随机搜索算法的比较分析

随机搜索算法是指在目标位置基本服从均匀分布的条件下，搜索轨迹随机且均匀散布在目标分布区域内，经过多次循环和迭代后在约束可行域内求解的一种搜索方法[10]。

本文用前面的算例，算法参数按照上文最初的参数配置进行实验，对随机搜索算法和基本粒子群算法的求解结果进行比较分析，得出的实验结果见表10，与随机搜索算法的比较趋势图如图3所示。

表10 与随机搜索算法的结果比较

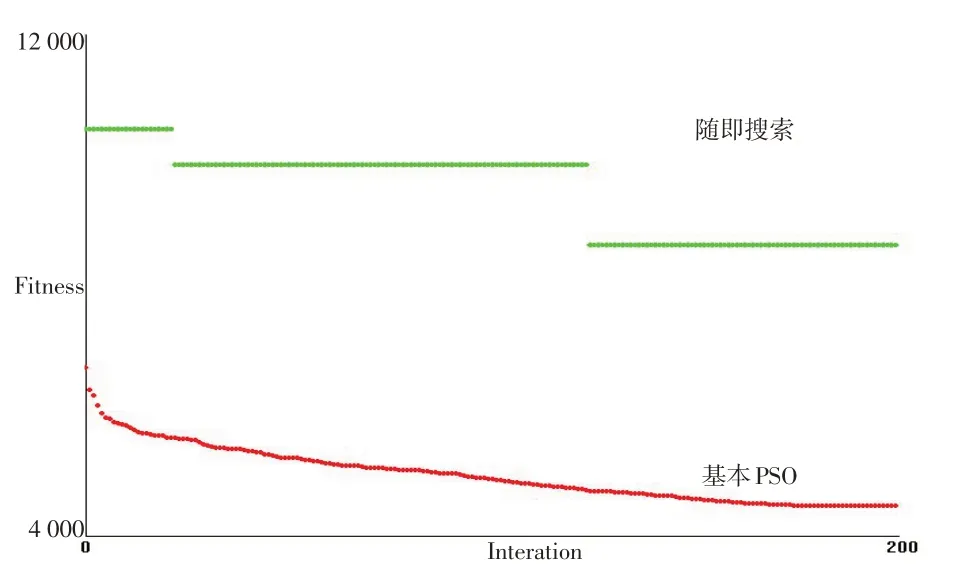
图3 与随机搜索算法的趋势图比较

从实验数据和趋势图可以看出，在一定的条件下通过随机搜索算法求得的结果远差于我们采用的基本PSO 算法，而在运算时间上没有太大的差别。随着循环迭代次数的不断增加，随机搜索得出的结果可能会更好，但是耗费的时间也将会不断增加，而且还不能保证可以得到较理想的结果。

随机搜索算法尽管简单易行，但是由于其效率低，难以找到最优结果。而基本PSO 算法却能够较快的、稳定的求得最优或较优的结果。

6.3 与穷举法的比较分析

穷举法是一种传统的搜索方法，其基本原理就是在一个可行域内，依次列出所有的可能情况，并对所有可能的情况进行判别，判断哪些是符合问题要求的，最后根据这些可能的情况找出问题的最优解[11]。

为了便于用穷举法与本文算法进行比较，我们取运输周期的前2个时段进行比较研究。这里，我们采用前面的算例，算法参数按照上文最初的参数配置进行实验，两种算法求出的实验结果见表11。

表11 与穷举法的结果比较

从实验结果来看，虽然穷举法得到的解稍优于本文PSO 算法的结果。但是，穷举法是遍历了问题的所有可能解后才得出最优的结果，而PSO 算法仅迭代95次后就收敛于最优解。且穷举法所耗费的时间远远大于PSO算法，研究的问题规模越复杂、循环迭代次数越多，那么，穷举法耗费的时间也将成几何倍数增长，而PSO 算法却能在较短的时间内收敛于最优解。对于应急物流来说，时间就是生命，必须在最短的时间内作出有效的决定，穷举法显然是不可能做到的，而本文用到的PSO算法因其简单、收敛速度快、易于实现等优点，具有更强的实用性和现实性。而且随着问题维数和复杂度的增加，PSO算法的优越性将更加明显。

7 结语

本文首先给出问题的描述和建模思路，在合理假设的基础上，以使在所有时段内、所有需求点、所有物品延迟满足而引起的损失最小为目标，构建了应急物流车辆调度的改进数学模型。其次根据应急物流车辆调度的特殊情况，设计了适合求解应急货物运输调度模型的粒子群算法，包括粒子的编码方法、适应度函数、参数控制和终止条件的确定等。然后通过一个算例对所建立的模型和算法进行数值模拟。然后比较分析了模型改进前后的实验结果数据，与其他算法和改进的PSO算法进行了比较，证明该模型及其算法的有效性。此相关研究成果可以为政府及行业企业在突发应急事件时进行车辆的有效调度提供科学依据。