提升小波改进阈值算法在输气管道泄漏信号降噪处理中的应用
2019-07-25高建丰周韶彤何笑冬
高建丰,2,周韶彤,何笑冬
(1.浙江海洋大学石化与能源工程学院,浙江 舟山 316022;2.临港石油天然气储运技术国家地方联合工程实验室,浙江 舟山 316022)
0 引言
众所周知,管道运输是当代的重要运输形式,同时也是天然气输送的主要工具,但是,天然气输送管道主要是由钢管所制,在一定情况下会发生泄漏等安全事故。例如2018年2月5日,广东韶钢松山炼铁厂发生煤气管道泄漏事故,导致多人死亡。2017年7月4日,松原市宁江区繁华路巷路施工过程中造成燃气泄漏,燃气公司在抢修时发生爆炸,事故造成多人遇难与重伤,其中14人重伤。2017年7月2日,中石油天然气输气管道晴隆沙子段因近期强降雨引发边坡下陷侧滑,挤断输气管道,引发泄露燃爆。初步查明造成8人死亡,35人受伤。2016年12月23日,北京朝阳区管庄路和常营路路口燃气管道泄漏引发严重火灾。类似的管道泄漏事故还有很多,造成一定的经济损失和人员伤亡。所以为了防止类似泄漏事故的发生,输气管道泄漏的检测监测显得尤其重要。工程上经常用的检测方法是负压波法,但是当输气管道遭到破坏产生泄漏点时,数据采集系统采集到的负压波信号会受到各种噪声的干扰,噪声的存在会对检测精度产生影响,所以为了提高检测的精确度,可以采用离散小波变换对检测到的负压波信号进行相关处理。例如,李帆等人利用小波分析方法,选择合适的小波基和分解尺度对燃气油管道泄漏信号进行降噪处理,可以较好的发现压力的突降点[1];李建平等人将小波分析理论引入到引黄工程中,提高了管道泄漏检测系统性能[2];倪伟等人在小波分析方法中引入阈值降噪理论对管道泄漏进行检测,提高了检测精度[3]。传统的离散小波变换之所以能够得广泛应用的关键原因是它有类似于傅里叶分析中快速傅里叶变换FFT的快速算法—Mallat塔形算法,这个算法中有三个重要环节:信号与QMF的卷积,隔点采样以及隔点插零[4]。但是由于实际正交滤波器的非理性频域特性,导致信号在与其进行卷积运算时时,会发生频谱混叠现象,同时在隔点采样和隔点插零环节中会出现虚假的频率成分[5-6]。并且几乎存在信号卷积运算的地方都要考虑信号的边界延拓问题,不同的延拓方式会产生不同的影响,所以在信号卷积过程中合理的选择信号的延拓方式也非常关键[7]。所以传统的基于傅里叶变换的小波分析方法存在着计算工作量大和复杂度高的缺点,而提升小波的出现可以有效的解决这个问题,相对于Mallat塔形算法,提升小波变换可以快速有效的对信号进行处理。近年来提升小波算法的应用也越来越多,但是应用在输气管道泄漏的负压波信号降噪处理中的较少[8-9]。综合上述分析,本文提出了基于提升小波改进阈值算法的输气管道泄漏信号降噪方法,从提升小波降噪基本原理出发,分析提升小波的降噪过程,引入改进阈值函数,确定最优提升小波基和最佳分解尺度,然后利用传统小波降噪方法和本文改进算法对现场采集的管道泄漏负压波信号进行降噪对比。
1 提升小波降噪基本原理和降噪过程
提升算法给出了双正交小波简单而有效的构造方法,基于提升算法的小波变换被称为第二代小波变换,所有能够用Mallat快速算法实现的离散小波变换都可以用第二代小波方法来实现,它使人们能够用一种简单的方法去解释小波的基本理论,用提升算法实现小波变换的最大优点就是将小波滤波器过程分解成简单的基本步骤[10]。提升小波算法主要分为3个阶段:分解、预测和更新。其中分解阶段就是将输入信号分成两个部分,其中最简单的方法就是将输入信号根据奇偶性分为奇数序列和偶数序列。预测就是在基于原始数据相关性的基础上,用偶数序列的预测值去预测或者内插奇数序列。更新则是为了使原始信号集的某些全局特性在其子集中继续保持,使得它保持原图的某一标量特性,例如均值、消失矩等不变[11]。
利用提升小波算法进行信号降噪主要分为以下几个步骤:首先选择一个合适的小波得到其提升方案,并将提升步骤添加到提升方案;其次对含躁信号选择合适的分解尺度进行分解,并提取分解后的相关系数;而后将分解得到的小波细节系数进行相关阈值处理;最后将逼近信号和经过阈值处理后的细节系数进行逆变换,得到降噪后信号。
2 影响消噪质量的关键因素的分析
2.1 阈值函数的选择
在信号降噪过程中,最关键的一步就是选择最佳的阈值函数,国内研究中用的最多的阈值函数为硬阈值函数以及软阈值函数,其原理也相对简单,其具体表达式分别为式(1)和式(2)所示:
(1)
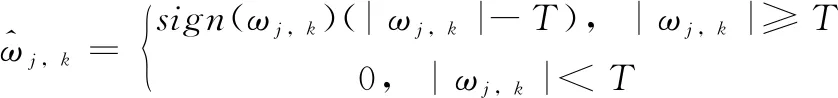
(2)
在硬阈值函数处理方法中,其主要是将小波分解系数中绝对值小于阈值的小波分解系数均归零处理,大于阈值的小波分解系数不变,而软阈值函数处理方法虽然也是将小波分解系数中绝对值小于阈值的小波分解系数均归零,但是对于大于阈值的小波分解系数不单单是保持不变,而是进行处理后应用。尽管通过硬阈值函数处理后的信号峰值信噪比较高,但是会有局部抖动的现象;软阈值函数的降噪结果看起来会相对光滑,但是会造成边界模糊,所以为了克服上述缺陷,引用了一种模平方处理方法改进阈值函数,将此函数应用在提升小波降噪中,可以在一定程度上提高降噪效果,其表达式如式(3)所示,阈值的选择满足式(4):
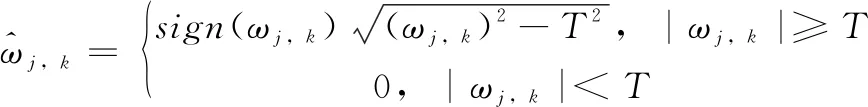
(3)
(4)
2.2 最优提升小波基的选择
不同于标准傅里叶变换,传统小波分析方法中所用到的小波函数拥有多样性,不同的小波基函数拥有各自的时域特征,所以选择不同的小波基函数作为提升小波基对同一个信号进行分析会产生不同的效果,我们可以通过对信号进行不同提升小波基函数的处理效果的对比来进行不同小波基降噪效果好坏的判断,进而确定最优的提升小波基函数。因此本文选取了不同小波函数作为提升小波基,在同一分解尺度下对同一信号进行降噪处理对比。选用系统自带函数进行染噪,染噪信号的信噪比是:24.2562 dB,选择的提升小波基函数为:haar、bior4.4、db2、db4、db5、db6、sym4,分解尺度均为4,阈值函数则为表达式(3)所示函数,其降噪处理结果如图1所示,同时表1是在同一分解尺度下,采用不同提升小波基函数进行同一分解尺度对信号进行改进阈值函数降噪处理后的信噪比。
从图表中可以看出,在同一分解尺度和同一阈值函数的前提下,当以db5小波函数作为提升小波基时,图像降噪的效果最好,同时信噪比也最大,其他小波函数作为提升小波基函数时会出现不同程度大小的失真现象,所以综合考虑可以把db5小波函数作为改进阈值算法的最优提升小波基。

表1 同一分解尺度下,采用不同提升小波基函数进行降噪处理后的信噪比
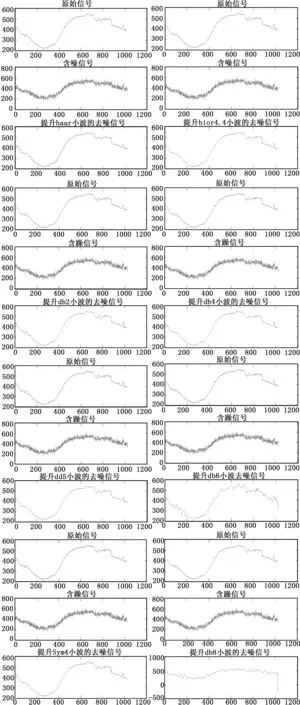
图1 不同提升小波基函数对信号的降噪对比图
2.3 分解尺度对信号降噪的影响
阈值函数的确定以及提升小波基函数的确定均会对信号的降噪处理效果产生一定的影响,同时可以在相关文献中发现,在进行小波分解时,不同的分解层数也会产生不同的影响。如果分解的层数过高会使有用信号的信息丢失,分解层数过低则又不能取得较好的降噪效果。所以本文在确定了最优阈值函数和最优提升小波基的基础上对信号进行不同尺度的分解,以确定最佳分解尺度,分解尺度lev=3、4、5、6,其降噪效果如图2所示,表2为对应分解尺度下对信号进行降噪后的信噪比。
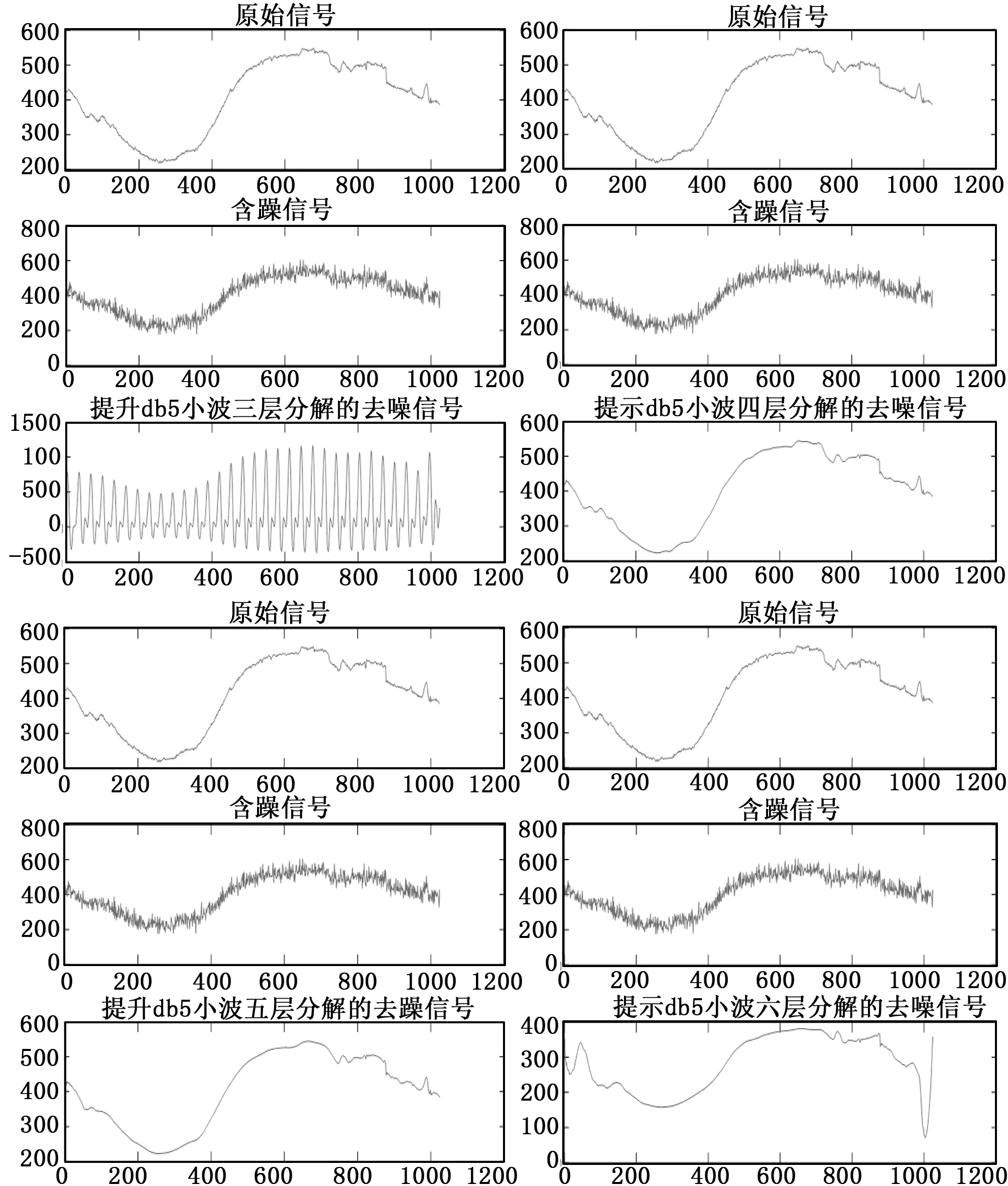
图2 不同分解尺度下的降噪效果对比图

表2 不同分解层数下对信号进行降噪后的信噪比
从图表中可以看出,当以db5小波作为提升小波,不同的分解尺度均会对信号起到不同程度大小的降噪作用,但是当分解尺度为3和6时,其信号出现严重的失真现象,分解尺度为5时,降噪后的信号相对与原信号更为平滑,而分解尺度为4时,降噪后的信号和原始信号图形基本一致,且信噪比最大,所以降噪效果最好。
3 分析实例
从上述对比分析中可以得出,以db4小波作为提升小波基对信号进行4尺度分解,并引入改进阈值函数对信号进行阈值滤波,可以得到较好的降噪处理效果,下面对现场采集的输气管道泄漏信号进行降噪处理。
3.1 现场数据的采集
图3为输气管道泄漏实验研究的实验装置,管道总长度1159 cm,其中泄漏点孔径大小由阀门控制,传感器1距离泄漏点270 cm,传感器2距离泄漏点680 cm。实验系统是由空气压缩机、气体缓冲罐、压力传感器、分离罐以及不同规格的钢管组成。为了保证实验安全,实验室采用压缩空气来代替天然气进行相关实验,其中空气压缩机用来提供压缩气体,气体缓冲罐用来稳定来自空气压缩机的压缩空气,分离罐用来释放气体。压力传感器采用CY301高精度数字式压力传感器,通过螺纹与管道连接,每1 ms采集一次数据。
在进行实验时,首先打开空气压缩机,三分钟后待其稳定打开出口阀,调节输气压力,输气压力为0.2 MPa。让气体进入气体缓冲罐中稳定,待管道内气体流量稳定时,打开泄漏点阀门,模拟泄漏孔径大小为0.25 cm。
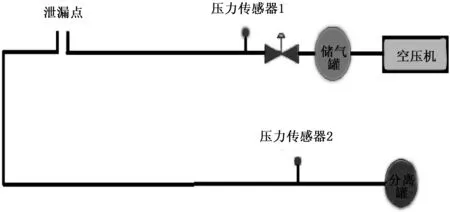
图3 实验系统示意图
3.2 现场实验数据的处理
当输气管道由于人为破坏或者自然原因等发生泄漏时,泄漏点处由于内外压力差的影响,会产生大量的气体损失,造成泄漏点处压力降低。由于气体的连续性,会在管道中产生负压波,并且沿着管道传播,此信号包含有泄漏点信息,比如发生泄漏的具体时间。输气管道首末的传感器接收到泄漏信号就能判断出管道是否发生泄漏。但是在实际运行中,传感器采集到的泄漏信号会受到各种噪声的污染,其有用信息会被噪声覆盖,导致传感器不能准确的捕捉到有用信息,从而不能对泄漏点进行准确的定位。所以为了提高输气管道泄漏点的定位的准确度,需要对传感器采集到的信号进行降噪处理。
由于上述实验是在实验室进行,其噪声量并没有实际输气管道所处环境中的高,为了模拟相似度更高,在不改变泄漏信号本质的前提下,对现场采集到的泄漏信号进行了一定的加噪处理,然后利用传统小波算法和提升小波改进阈值算法对信号进行降噪对比,其降噪结果如图4所示。
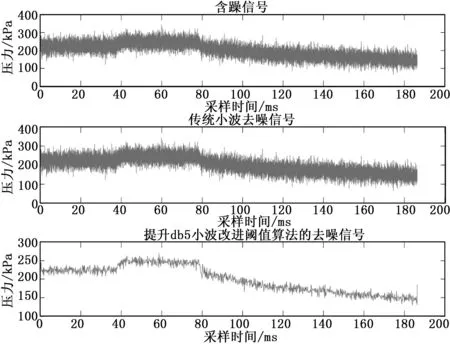
图4 传统小波去噪与提升db5改进阈值算法去噪对比图
在进行降噪处理效果评价中,最常用的就是利用信噪比大小确定其降噪效果的优劣,但是信噪比计算一般需要知道原始的“干净”信号,然而在实际工程应用中,并不知道采集到的信号的原始信号,所以不能简单的通过信噪比去判断其降噪的好坏,但是通常可以采用其他量化指标来评价去噪质量,比如降噪前后的图像对比。从图4可以看出,利用提升小波改进阈值算法的降噪方法对输气管道泄漏信号进行降噪的效果明显优于传统小波方法降噪,虽然传统小波方法可以去除一定的噪声,但是对于输气管道泄漏信号,提升小波改进阈值算法则可以将泄漏信号中的噪声进行基本消除,将信号突变点更明显的显示出来,所以将提升小波改进阈值算法应用在输气管道泄漏检测中,可以为泄漏点的检测和定位提供基础。
4 结论
提升小波分析方法在进行信号处理时较传统小波分析方法具有一定的优势,但是在利用提升小波方法对信号进行降噪时,其提升小波基函数,分解尺度以及阈值函数的选择均会对信号处理的效果产生一定的影响。仿真和实验结果表明:利用提升db5小波对信号进行4层分解,并引入改进阈值函数,能够在一定范围内提高信号的信噪比,达到更好降噪效果,而且在实际应用过程中也能消除一定的噪声,对提高泄漏信号的检测精度具有一定的应用价值,但是其噪声并没有得到完全的消除,如何在此基础上进行奇异点的准确捕捉还有待于进一步研究。
