基于超宽带技术的轨道交通定位算法研究

(1.比亚迪通信信号有限公司，广东 深圳 518000； 2.北京师范大学 核科学与技术学院，北京 100875)

0 引言

超宽带无线电定位技术具有大带宽、抗干扰能力强、多径分辨力高、测距响应速度快、精度高(厘米级)、功率谱密度低、系统简单、成本低等特点[1]。UWB模块通讯距离较短，适用于轨道交通车辆进站定位、局部区域的车辆调度和无人驾驶。安全高效运行始终是轨道交通系统的重要主题和发展方向，而系统的安全高效运行要求定位技术响应速度快、精度高、结构简单。对于轨道交通的车站环境和隧道环境，GPS定位技术因为受到遮挡难以有效实现高精度定位。轨道交通目前广泛应用基于应答器加里程计的定位方式，其在定位精度和闭塞效率方面仍有一定的局限性，UWB高精度连续定位可作为辅助定位技术，可进一步提高安全性和运营效率。

典型的无线技术定位算法包括质心定位法、解析法、最小二乘法、Taylor法等[2-5]。在现有的研究中，质心定位法计算精度低，算法灵活度低；有测距误差条件下，两定位圆之间无交点的情况，无法应用解析法；已有的研究讨论的都是几个地面参考基站所包围区域的定位问题，在包围区域边界附近定位精度变得较差；对于包围区域外部的定位问题，很少见到相关研究。本文根据轨道交通的特点和UWB模块特性，将轨道方程约束条件和连续性约束条件加入最小二乘法、Taylor递归法、Kalman滤波当中，应用五个步骤计算定位结果。先用最小二乘法粗略计算出位置，并将其作为迭代初值代入有轨道方程约束的Taylor递归法，计算出迭代后的坐标，最后应用具有速度约束性的Kalman滤波法，将迭代后的坐标进行数据滤波修正，得到比较精确的坐标位置，最后用曲线近似积分法计算出待测物体的行驶路程。另外，应用待测物位置连续性约束条件，第二次及以后定位计算时，Taylor递归法的迭代初值也可取上个位置的坐标。轨道方程事先由拟合得到。本论文算法在地面参考基站包围区域内、外均达到了一致的定位精度；对于非视距情况及多径效应产生的较大测距误差，也能消除其对定位精度的影响。

1 定位系统的构成

UWB定位方法主要有到达角度定位(angle of arrival, AOA)、信号强度分析法(received signal strength indication, RSSI)、到达时间定位(time of arrival, TOA)、到达时间差定位(time difference of arrival, TDOA)[6-7]。前两种定位方法设备复杂度比较高，TDOA法需要在地面服务器端计算定位结果。如图1所示，本文采用TOA法，移动站布置在待测物体(列车)上，地面参考站布置在轨旁，参考站两两之间在水平和竖直两个方向上均间隔一定距离(不小于2 m)。灵活的布点方式有利于降低工程实施难度，特别是对于空间有限的高架轨道区间、站台区域、隧道区段等。

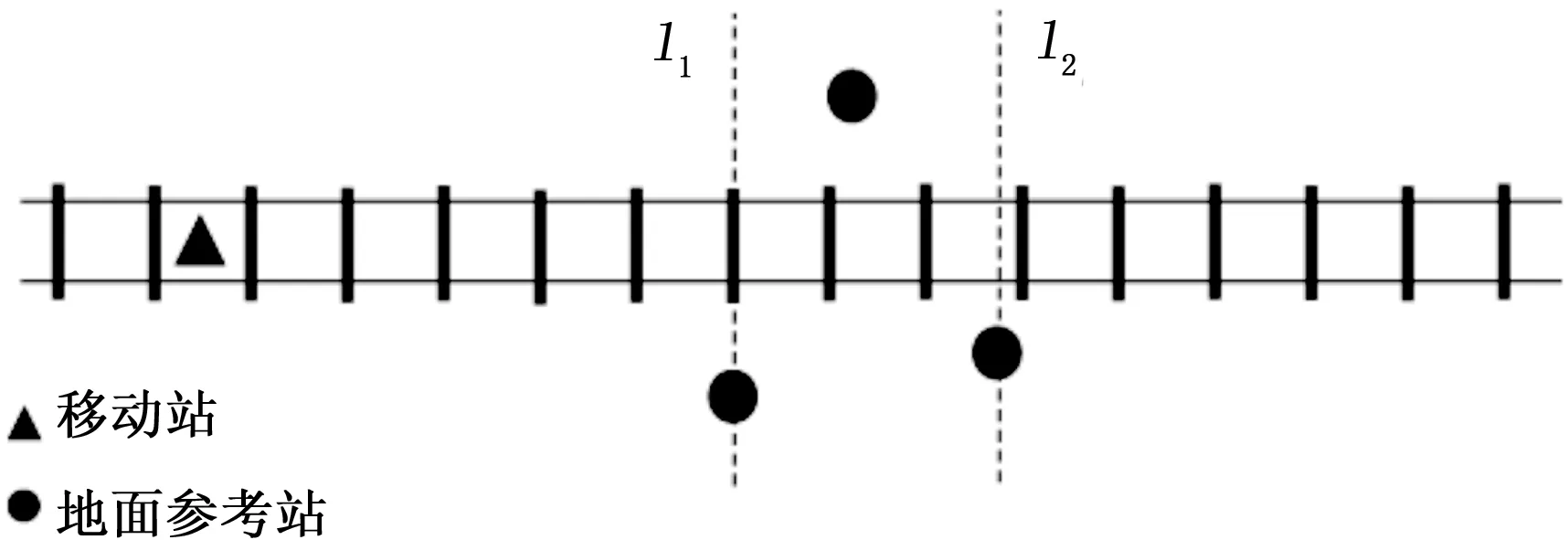
图1 基站布置示意图

待测物与其它地面参考站的距离由信号到达时间乘以电磁波传播速度得到，从而计算自身坐标位置。对于静态物体的定位，增加参考站的数量可提高定位精度[8]，但参考站数量增多会增加测距次数，增加时延，对于以较快速度运动的物体，会导致较大时延误差。对于二维场景，至少需要3个参考站，对于三维场景，至少需要4个参考站，为简化问题，本文采用3个基站。本文就一段轨道区间进行研究，对于全线定位的实现可依此类推，沿途间隔布置参考站。

2 定位算法原理

2.1 算法基本思想

待测物的位置可由以下几个条件确定：①基本条件：各参考站的位置及其与待测物的测距距离；②轨道曲线方程约束：列车在轨道上行驶；③移动位置连续性约束：列车行驶过程不具有跳跃性；④速度连续性约束：在数十ms的间隔时间内，列车运行速度不具有很大的跳跃性。由基本测距条件和约束条件，联合使用最小二乘法、Talor迭代法，以及Kalman滤波，可计算出待测物坐标，或者待测物(列车)距车站的路程，或者列车距离闭塞区间端点的路程(列车控制系统通常以列车距轨道上某一点的路程做定位参考)。

2.2 定位算法整体流程

有约束条件的定位融合算法整体流程如图2所示，共有五个步骤。事先用样条函数[9]对轨道曲线进行拟合，用最小二乘法粗略计算出位置坐标，并将其作为迭代初值(第二次及以后定位时也可用上次的位置坐标作为迭代初值)代入有轨道方程约束的Taylor递归法，计算出迭代后的位置坐标，最后应用具有速度约束性的Kalman滤波法，进一步进行数据滤波修正，得到比较精确的定位坐标，最后用辛普森积分法或Cotes积分法计算出本次定位坐标与上个位置的坐标之间的路程，这样每定位一次积分出一小段路程，累积的结果即待测物体的总行驶路程。分小段积分的优势在于减少计算量。

图2 定位算法流程图

2.3 最小二乘法

已知各参考站位置(xi,yi)及各参考站到待测物的水平距离ri(可由测距距离di、参考站与移动站的高度差hi构造直角三角形求得)，当测距无误差时，待测物位置(x,y)满足以下关系：

(1)

以各地面参考基站为圆心，以待测物与各地面参考基站测距距离为半径画圆，如图3所示，图中黑点表示待测物实际所在位置，因为实际测距存在误差，三个圆并不交于一点。方程组(1)无解析解。两两圆的位置关系可能是相交、相切、相离、包含关系中的一种。

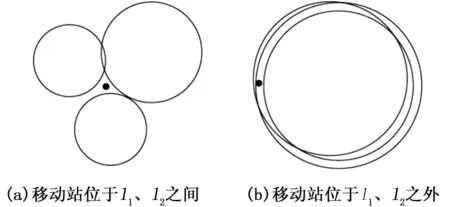
图3 有测距误差存在时定位圆关系示意图

当待测物位于参考基站所包围区域时，定位圆的关系如图3(a)所示；当待测物位于包围区域外部时(移动站在参考站有效测距范围内)，如图3(b)所示，几个定位圆重叠度比较高，无法应用几何法计算，采用单一的方法计算误差也比较大。(1)式为超定方程组，可找一个解使方程组误差平方和最小。将其转化为矩阵形式：

(2)

其最小二乘解为：

X=(ATA)-1ATb

(3)

2.4 有轨道方程约束的Taylor迭代法

对于定位圆重叠度比较高的情况，需要更精确的求解。定位点可进一步由Taylor递归算法[10]求得。由待测物(x,y)到地面参考站(xi,yi)的距离与水平距离ri的差可构造方程：

(4)

工程上，轨道曲线方程常用样条函数拟合，保证方程连续可导。设拟合的轨道方程为：

y=f(x)

(5)

由方程(4)、(5)求一点(x,y)使得Q取得最小值。将(5)代入(4)，令x=x0+Δx，并在迭代初始点x0进行一阶泰勒展开得：

Q-R=h-Gδ

(6)

R为Taylor展开余项向量，

δ=[Δx]，式(6)的最小二乘解为：

δ=(GTG)-1GTh

(7)

第二次递归时，令x0=x0+Δx，重复以上过程，迭代直到Δx小于一个设定的阈值，此时的(x0,f(x0))即为定位点的坐标。

2.5 曲线积分近似法

可采用累积积分的方法计算待测物的行驶路程。用直接积分法可能无法对实际的轨道曲线函数进行曲线积分，可采用辛普森积分法或Cotes积分法。

辛普森积分法具有三阶代数精度，Cotes积分法具有五阶代数精度，对于更高阶数的方程，这两种积分方法能以较少的计算次数获得很高的计算精度。辛普森求积公式[9]为：

(8)

Cotes积分公式[9]为：

32f(a+3h)+7f(b)]

(9)

2.6 卡尔曼滤波算法

由于电子设备的本底噪声、电磁波传播过程中具有多径效应、非视距情况，UWB测距模块表现出以较小概率出现大的测距误差。需要对定位结果进行校正。Kalman滤波[11]为某时刻的状态值与当前时刻以及之前各时刻的测量值建立关系，是对高斯过程非常有效的一种实时滤波方法。卡尔曼滤波分为预估和校正两个过程。预测过程为：

(10)

(11)

(12)

(13)

(14)

(15)

3 实验及分析

3.1 UWB模块测距实验与性能分析

本研究选用的UWB模块为Time Domain公司的PulsOn 440，它是一种工作波段在3.1 G到4.8 G之间的超宽带无线收发器，采用双向飞行时间(TW-TOF)方式进行测距。系统时钟同步精度达1 μs，宣称的测距精度为2～5 cm，在自由空间的测距距离为240 m，测距速率最高为125 Hz，发射功率为-13 dB。

在一条车辆较少的公路上，对P440模块进行了测试。公路两旁有树木、建筑物、空调外机，公路上有少量汽车通行，测试的同时，手机在模块旁通话。使两模块在不同距离下测距次数超过1000次，采集数据并对数据进行统计分析，如表1所示，表中误差为测距距离减去均值，测距距离的单位为mm。

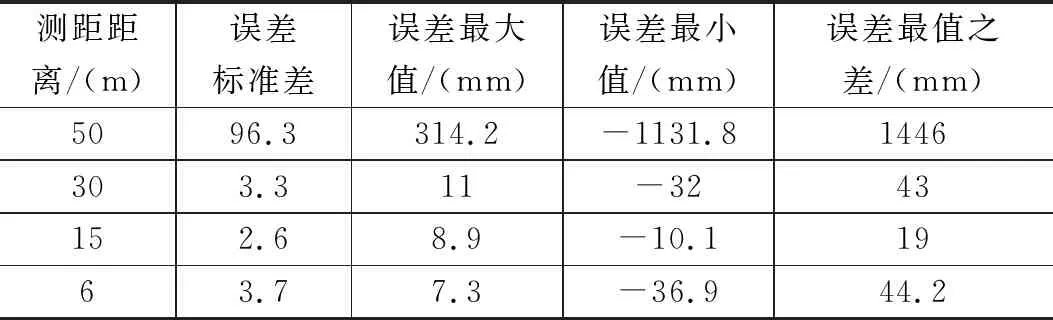
表1 测距性能指标统计表

由表1中数据知，测距距离越短，误差的标准差越小，该模块测距精度与稳定性越好。

图4、图5分别为测距距离50 m、15 m情况下误差的分布图，图中曲线为其对应方差的正态分布曲线。

图4 测距距离为50 m的情况下误差分布图

图5 测距距离为15 m的情况下误差分布图

50 m的距离下，测距1540次，误差绝大部分分布在-40 mm到50 mm的区间范围内，小于-400 mm的情况只出现12次，占比0.78%。出现较大误差是由电磁波传播的多径效应与非视距情况导致。15 m的距离下测距1185次，测距误差均在-1～1 cm范围内。统计结果表明测距误差较大的概率比较小。基于P440模块以上特点，本文采用高斯误差近似代替实际误差进行分析计算。

3.2 计算分析

为了验证算法效果，分别在50 m、15 m对应的两种测距误差(即N(0，9.632)、N(0，0.262)分布的高斯误差)情况下进行了相关计算分析，为方便表述，后面直接用方差来代表高斯测距误差。如图6所示为参考基站位置及轨道曲线示意图。

图6 参考基站位置及轨道曲线示意图

轨道曲线方程为y=0.00001x2+10，三个参考基站的坐标为(4500,13)，(5000,460)，(5500,113)，待测物运动的起始坐标为(0，10)，终止坐标为(10000,1010)(单位：cm)，并且令待测物沿轨道变速运动。

3.2.1 对最小二乘法的效果分析

由最小二乘法计算待测物的坐标，并比较计算坐标与实际坐标的距离差DISE。如图7为测距误差N(0，9.632)分布的最小二乘法定位误差曲线，在基站附近区域，定位误差很小，基本在25 cm以下。两侧呈发散趋势，这是由于远离三个参考基站的区域，线性漂移比较严重，如图3(b)所示情况。即在参考基站包围区域外部，简单的算法无法保证定位精度。

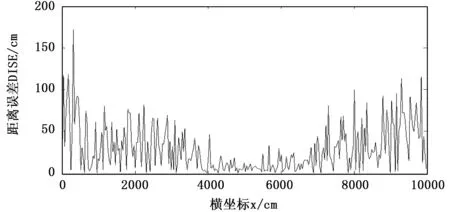
图7 测距误差为9.632时最小二乘法定位误差曲线

3.2.2 经过迭代前的步骤与Taylor迭代法计算的效果分析

图8、图9是分别在两种高斯测距误差情况下，经过最小二乘或位置连续性条件给定迭代初值，再由Taylor迭代后定位误差的曲线。图8相较图7，经过轨道方程约束的Taylor法迭代计算后使定位误差得到了很大改善，距离误差DISE都在20 cm以下，而且绝大部分定位点误差在10 cm以下。在参考基站包围区域内外，达到了一致的定位精度。

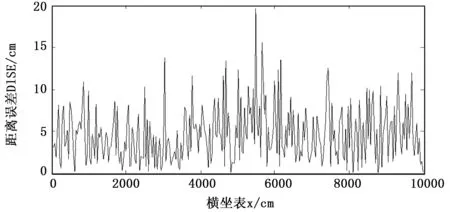
图8 测距误差为9.632时Taylor迭代后定位误差曲线

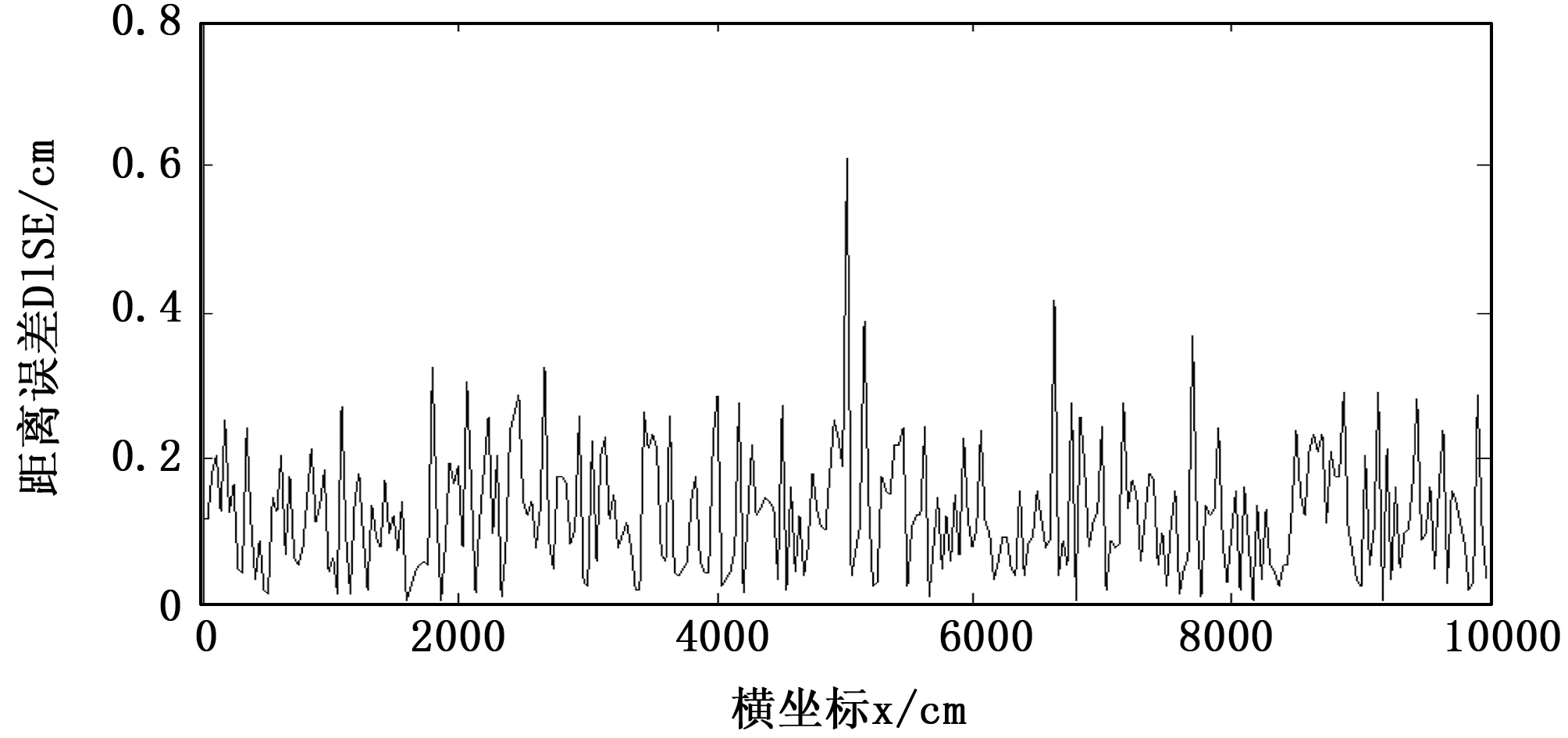
图9 测距误差为0.262时Taylor迭代后定位误差曲线

图9的定位误差普遍在0.8 cm以下，测距误差的方差越小，定位精度明显提高，因此P440模块近距离定位精度极高。因此，提高模块测距精度与测距稳定性，会显著改善定位效果。

图10为迭代次数统计曲线，Δx的阈值设置为0.1，如继续进行迭代，Δx会继续减小，但定位误差并无明显改善。迭代次数普遍在3次以下，迭代收敛很快，计算量比较少。

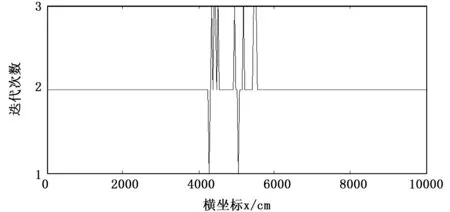
图10 测距误差为9.632时Taylor迭代次数统计曲线

3.2.3 经过Kalman滤波前的步骤与Kalman滤波计算

对于小概率出现的远大于误差均值的测距误差，需要对Taylor迭代后的数据进一步进行滤波改善。滤波初始状态向量取为：

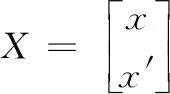
如图11所示，对比图8，定位误差进一步得到显著改善，距离误差降到10 cm以下，且绝大部分定位点距离误差小于5 cm。与前面测距实验统计结果对比可知，Kalman滤波有效改善了小概率出现的大的测量误差。

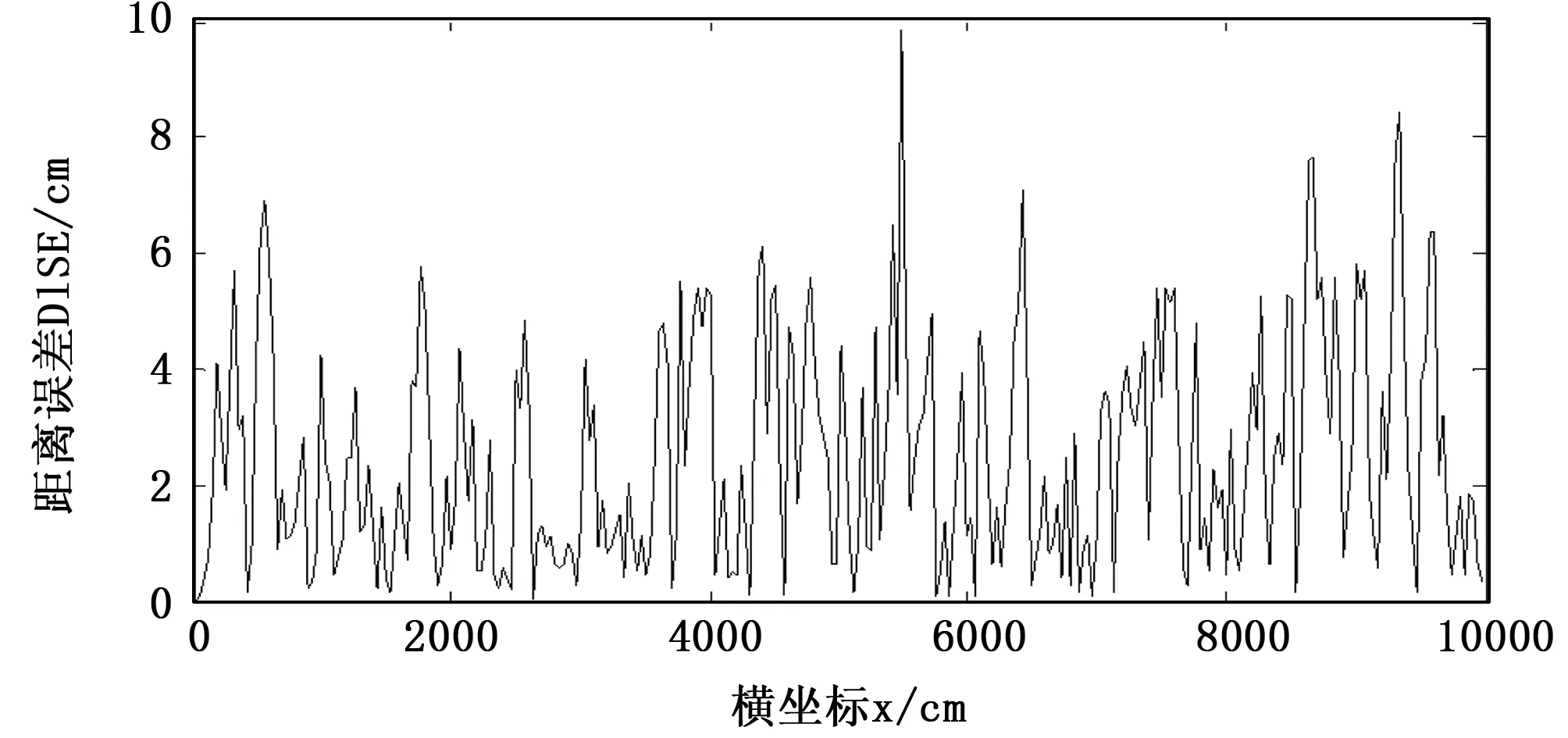
图11 测距误差为9.632时Kalman滤波后定位误差曲线

图12为滤波后的路程误差PE曲线，路程误差为实际路程与计算路程之差的绝对值。本文的定位方法可以很好地适用于基于路程定位的轨道交通信号控制系统。

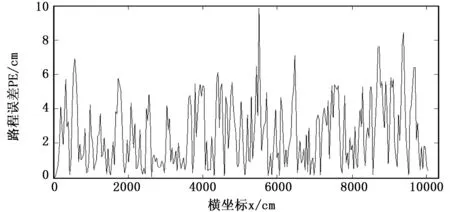
图12 测距误差为9.632时Kalman滤波后路程误差曲线

4 结论

本论文所研究的定位方法复杂度低，UWB模块响应速度快，参考点布置灵活，且算法自动化程度高、计算量少、精度高，比较适合于基于路程定位的轨道交通系统，对局部区域内运动物体的实时无人驾驶定位也具有参考价值。滤波算法中涉及到一些先验参数，需配合其它传感器如惯性导航或者速度传感器使用，利用加速度和速度等信息，将提高定位精度和稳定度。