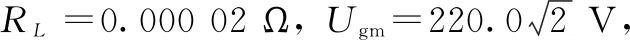单相光伏微网逆变器的建模与电流跟踪数值模拟

罗 丹 1，廖志贤，黄国现，韦笃取，蒋品群

(1.广西师范大学 漓江学院，广西 桂林 541006； 2.广西师范大学 电子工程学院，广西 桂林 541004)

0 引言

大量可再生能源的接入以及负载的多样化，导致电网面临新的问题和挑战，典型的如风能、生物质能、太阳能、波浪能等新能源，具有输入特性不一、间歇式的特点，再如新能源汽车、电动的工业自动化设备等新型负载，也有随机、非线性、动态的特点，特别在新能源时代，有些负载具备能量双向流动的能力，电网越来越走向对等化、智能化、网络化方向发展[1-2]。能源互联网是构建未来坚强、智能的能源网络的绝佳方案，其中，光伏微网是其重要的组成部分[3]，光伏微网逆变器的性能与能源互联网的稳定运行息息相关，为此，光伏微网逆变器的分析方法和控制方法越来越得到研究者们的广泛关注[4-6]。

光伏微网逆变器在能源互联网的背景下，如何找到更合适的分析和建模方法[7-9]，是一项重要课题。光伏微网逆变器通常工作在多机互联组网的情况下，从网络的角度对其进行分析、数值计算，以得到其网络动力学行为特性[10-12]，显得非常重要，因此，建立光伏微网逆变器的数学模型，对于进行数值模拟分析、研究是非常有意义的。

对光伏微网逆变器进行建模，主要分为两种方法，第一种方法是根据逆变器的开关电路模型，建立其分段光滑模型[13-14]，这种方法考虑了逆变器内部的开关电路细节，建立的模型较为精确。第二种方法是，重点关注逆变器与网络的耦合方式，建立其小信号模型[15]，研究网络组网时的控制方法和性能分析。上述两种方法中，第一种方法适合在对单个逆变器或者个位数数量级的逆变器组网情况下使用，效果较好。第二种则非常适合于进行大规模的多机组网建模分析时使用。

能源互联网背景下的光伏微网逆变器均在组网情况下进行分析[16-17]，其联机数量通常大于100台，且基于数字控制方法，如基于预测控制、数字PI控制、滑膜控制和模糊控制等进行电流跟踪控制。

基于上述的研究背景，本文首先对单相光伏微网逆变器的电路进行原理分析，然后从其简化电路模型中的电压回路方程，建立其微分方程，接着建立其四阶龙格-库塔法的迭代模型，最后，采用最广泛的线性预测方法对模型进行数值模拟，验证模型的有效性。本文建立的光伏微网逆变器模型、四阶龙格-库塔法的迭代模型及其在线性预测控制下的数值模拟，对大规模微网逆变器的组网数值模拟分析，具有较大的参考价值和实践指导意义。

1 光伏微网逆变器的数学模型分析

1.1 单相光伏微网逆变器电路分析

光伏微网逆变器输出端与微网公共端相连接，由于光伏电池阵列具有电流源特性，且电能具有间歇性的特点，因此，光伏微网逆变器通常工作在电流源模式，即需要进行电流跟踪控制。光伏微网逆变器的输出电流质量是一个重要的参数，其输出电流应是一个与微网电压、频率、相位同步的正弦波信号。光伏微网逆变器并网运行的简化电路如图 1所示。uinv为光伏微网逆变器输出电压，ug为微网电压，RL为线路等效电阻，L为输出耦合电感，io为光伏微网逆变器注入微网的电流。

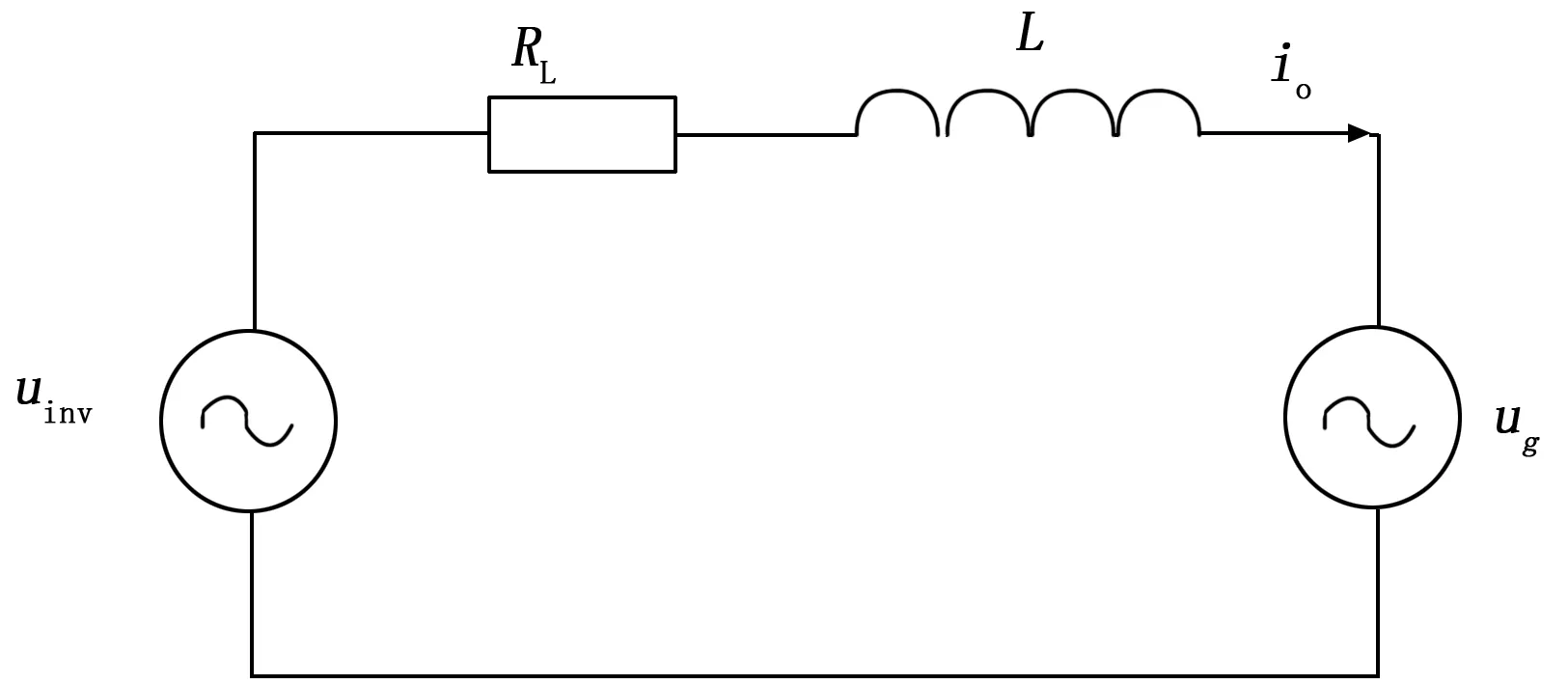
图1 光伏微网逆变器并网运行简化电路

在设计实际系统时，线路等效电阻RL的最佳阻值应该趋向于0，通常设计得非常小，为便于分析和计算，可忽略其损耗，得到光伏微网逆变器输出矢量图如图 2所示。耦合电感L导致光伏微网逆变器输出的电压uinv与为微网电压ug存在α相位差，微网逆变器控制系统将控制为光伏微网逆变器输出电压uinv，使光伏微网逆变器注入微网的电流io对微网电压ug进行跟踪，使得io与ug频率和相位相同。

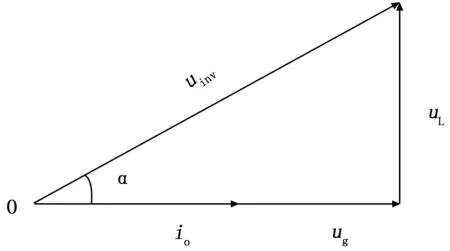
图2 光伏微网逆变器输出电压、电流信号矢量关系图

1.2 光伏微网逆变器的数学建模分析

由图1光伏微网逆变器的简化电路模型可知，输出电流io(t)实际上是输出电感的电流，其大小主要由光伏微网逆变器输出电压uinv(t)和公共电网电压ug(t)的差值，即电感两端uL决定。根据单相光伏微网逆变器电压回路，可建立其微分方程：

(1)

式中,L为光伏微网逆变器输出耦合电感，RL为光伏微网逆变器输出线路的等效电阻。

单相光伏微网逆变器的输出方程为：

y(t)=io(t)

(2)

2 基于四阶龙格-库塔法的迭代模型

在龙格-库塔法中，四阶法由于兼具精度高和速度快的优点，在对微分方程数值求解中最为常用，其迭代方程如下：

(3)

式中，h是积分步长，k0和k3分别是时间段开始、终点的斜率，k1和k2是时间段中间的斜率。令x(t)=io(t)，本文研究的光伏微网逆变器的微分方程如下：

(4)

其中:微网的电压表达式如下：

ug(t)=Ugmsin(ωt)

(5)

光伏微网逆变器的输出电压uinv(t)，是系统控制输入信号。

综上，更具体的迭代方程如下：

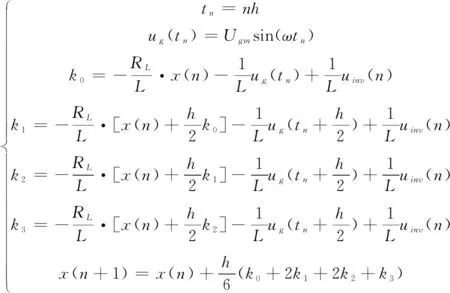
(6)

设置好积分步长h后，启动数值计算程序，显然，时间t与迭代次数n有如下关系：

tn=nh

(7)

迭代模型建立后，可用计算机数值方法进行编程、模拟和分析，随着迭代次数n的增加，计算出迭代时间点tn，带入迭代方程，即可获得单相光伏微网逆变器方程的数值解。

3 数值模拟结果及分析

3.1 数值模拟时采用的光伏逆变器控制方法

线性预测方法在光伏逆变器的电流跟踪控制中的已经得到了广泛的应用，其原理是利用历史采样值对下一个周期的电网电压及输出电流进行前向预测。由前文的光伏微网逆变器的数学模型可知，uinv(t)是系统控制变量，io(t)是系统输出。

微分方程(1)的解析解如下：

(8)

对(8)式进行离散化，可假设采样周期为TS，令t=(k+1)TS，t0=kTS，io(k)=io(kTS)，得其离散方程：

[uinv(τ)-ug(τ)]dτ

(9)

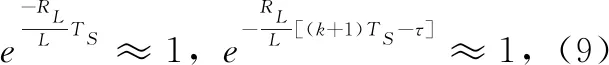
(10)

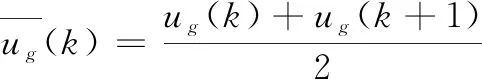
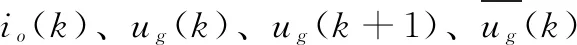
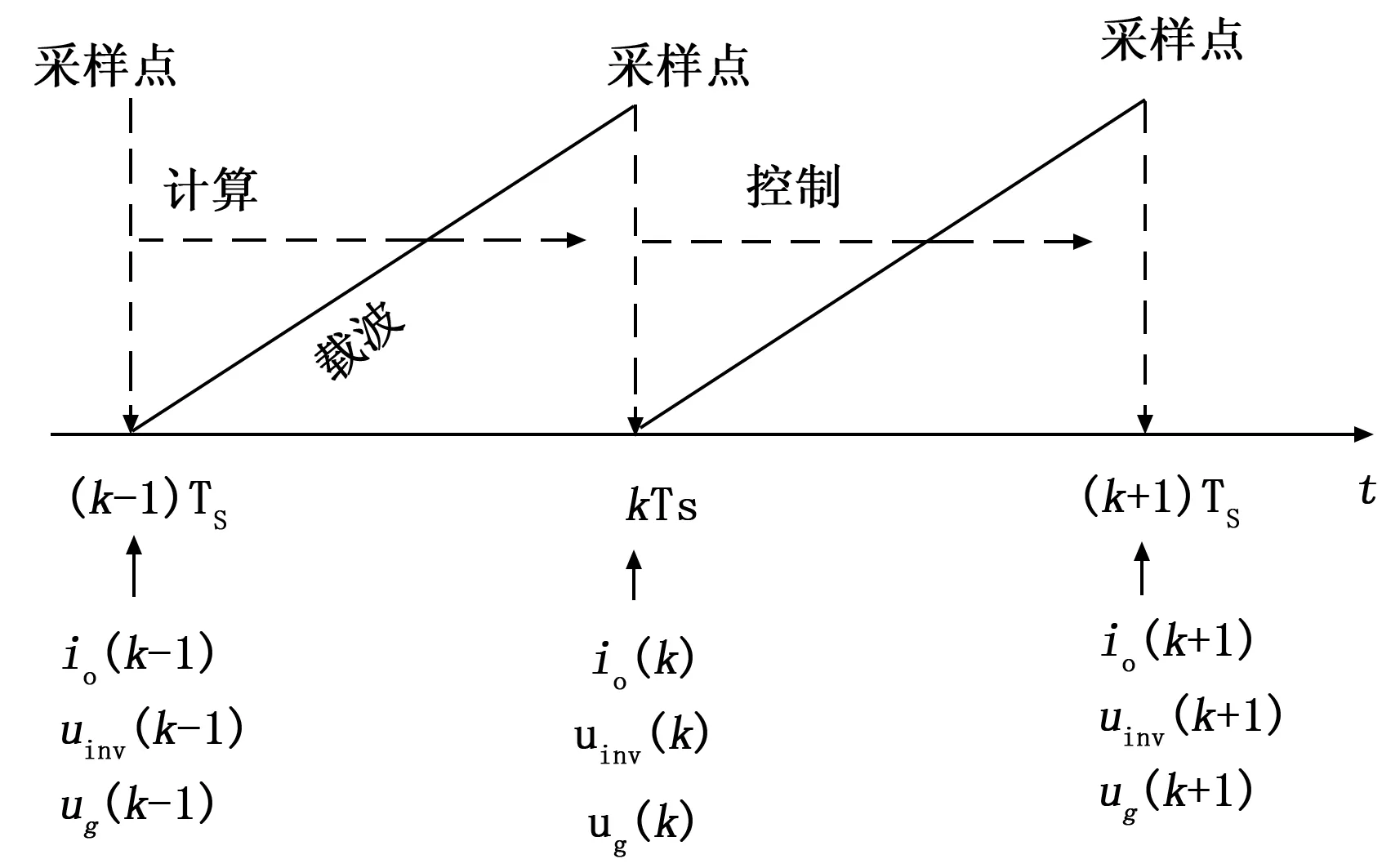
图3 线性预测控制方法示意图

利用(10)式，根据线性预测原理[18]，可得到控制项的表达式如下：

(11)

式中，令io(k+1)=iref(k+1)，则光伏微网逆变器在kTS时刻输出电压uinv(k)，可使时间点(k+1)TS输出的电流io(k+1)等于参考电流iref(k+1)，实现光伏微网逆变器的电流跟踪控制。

3.2 数值模拟结果与分析

根据式(6)迭代方程和式(11)的控制项方程，各个参数取值如表1。

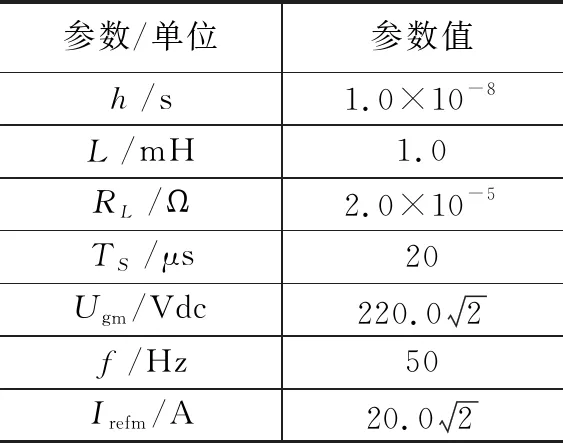
表1 数值模拟的参数取值

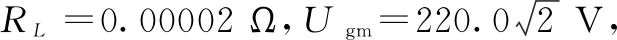
在上述参数条件下，利用3.1节式(11)的线性预测控制方法对所建立的光伏微网逆变器模型进行数值模拟，得到光伏微网逆变器的输出电流波形如图4所示，将时域上0.022～0.028 s时间段的波形放大显示，可见电流有一定的纹波，但整体波形失真度很小，由图 5可见，其总谐波失真度(THD)为1.76%。光伏微网逆变器输出电流的误差波形如图6所示，绝对误差的绝对值约为1 A， 说明预测控制方法的输出电流绝对误差较大，且呈现误差信号幅度恒定的特点，但总谐波失真度较小，可以满足并网标准(国家标准为≤5%)。

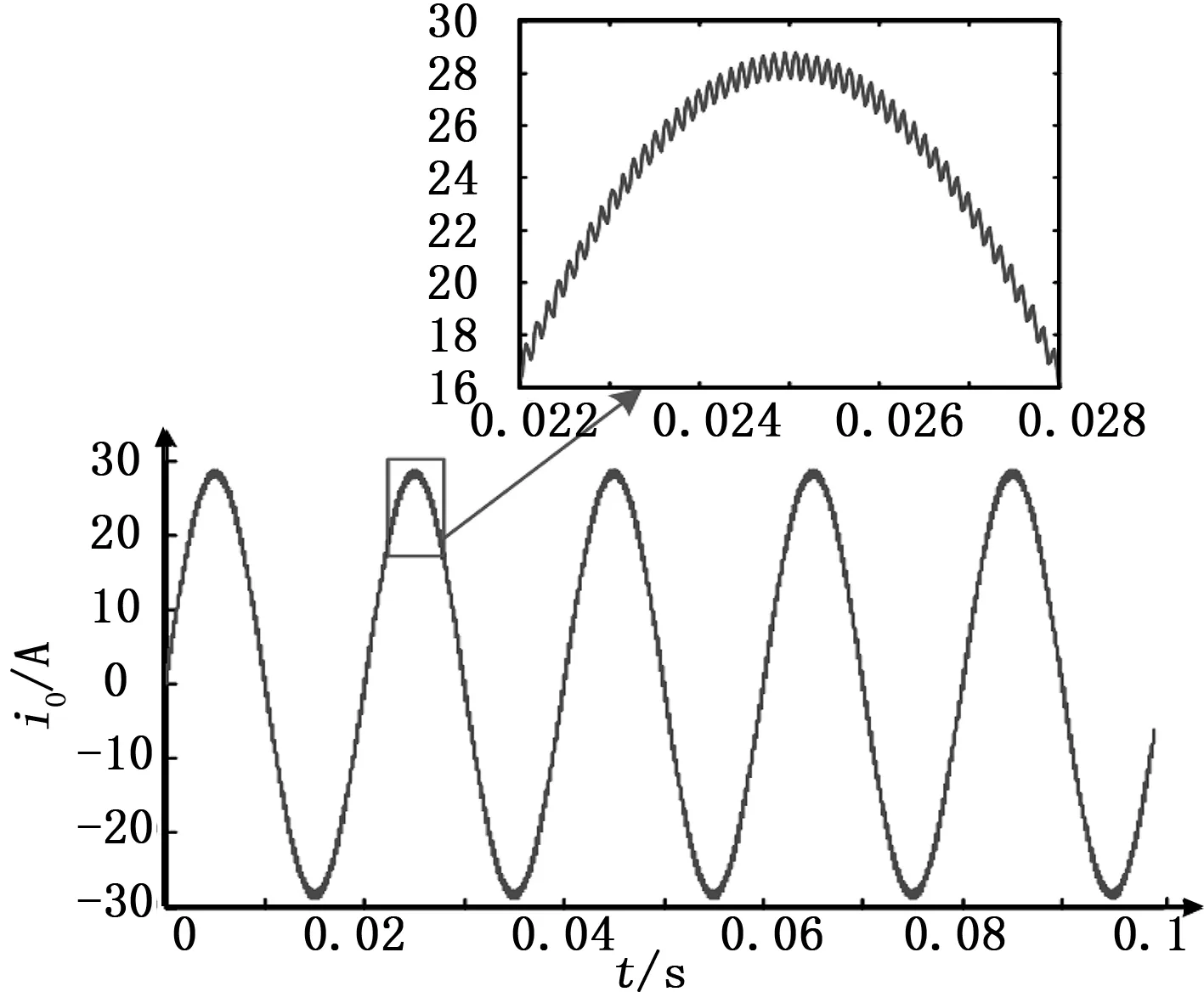
图4 光伏微网逆变器输出电流波形

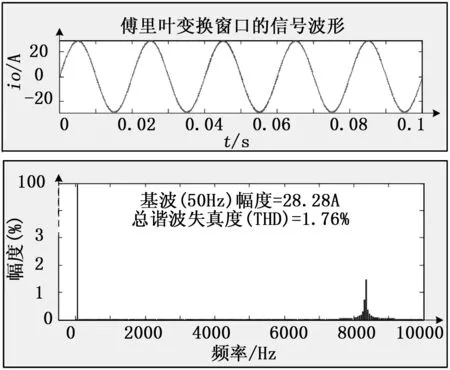
图5 光伏微网逆变器输出电流总谐波失真度

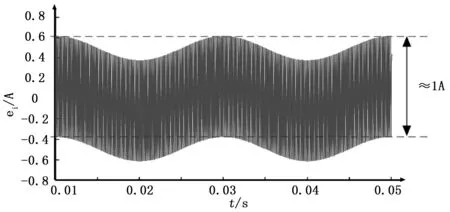
图6 光伏微网逆变器输出电流误差波形

光伏微网逆变器输出电压uinv(t)波形如图 7所示，将时域上0.022～0.028 s时间段的波形放大显示，如图8可见，电压波形的纹波振幅达到50 V，说明在控制器调整控制信号的过程中导致逆变器输出电压有较大的波动，整体的失真度较大，由图 9可见，其总谐波失真度(THD)为3.99%，满足国家电网谐波标准(≤5%)。

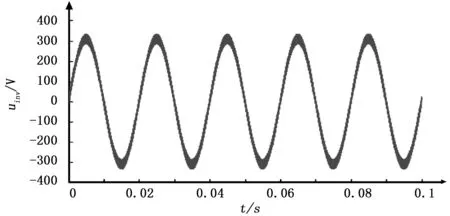
图7 光伏微网逆变器输出电压波形

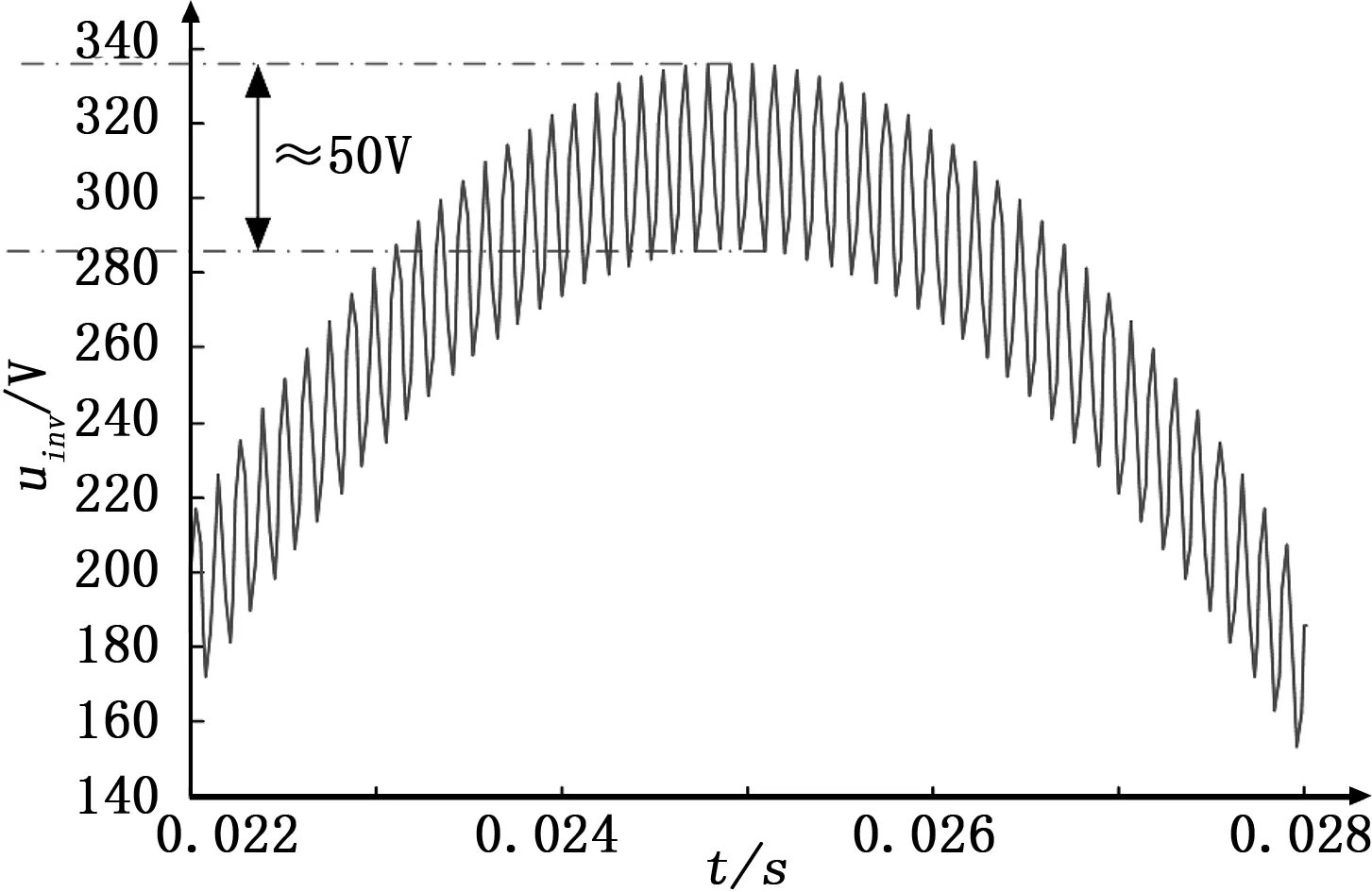
图8 光伏微网逆变器输出电压波形放大图

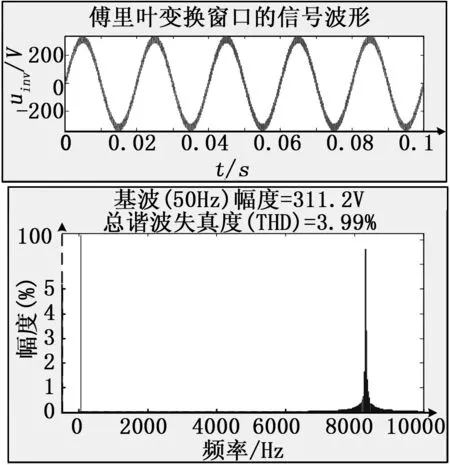
图9 光伏微网逆变器输出电压总谐波失真度

4 结论