基于灰狼优化算法和最小二乘支持向量机的信用评估
2019-07-24周敏
周 敏
(1.中国民用航空飞行学院 计算机学院,四川 广汉 618307; 2.西南财经大学 经济信息工程学院,成都 610074)
信用评估是金融机构进行信用风险管理的重要手段之一,其基本思想是利用贷款或信用卡申请人提交的信息和第三方提供的信息来计算申请人的信用风险,将其划分成不同的风险等级,并以此作为贷款或信用卡审批的依据[1]。“信用评估对金融机构盈利来说至关重要,即使是在信用评估精度上提高了1%,也会大幅度减少金融机构的损失”[2]。
信用评估实质上是模式识别中的分类问题,依据申请人的特征,例如年龄、性别、婚姻状况和收入等,将申请人分为好客户或坏客户。训练模型时,根据历史数据发现规律,得到分类模型,然后通过模型对未来贷款人的违约风险进行预测。因其重要性,传统的统计方法和现代数据挖掘方法被广泛地应用到信用评估模型中。
线性判别分析(linear discriminant analysis, LDA)[3]和逻辑回归分析(logistic regression analysis, LRA)[1]是统计技术中2个具有代表性的方法。LDA是第一个用来建立信用评估模型的工具,并且被广泛作为基准方法。LRA是一种概率统计分类模型,它也可以用来预测二元分类问题,根据一个或多个变量来预测被解释变量的类别。理论上来讲,数据挖掘或机器学习中的任何分类方法都能用于信用评估,例如惰性学习方法K最近邻(K-nearest neighbor, KNN)、基于信息熵的决策树(decision tree, DT)、基于核方法的支持向量机(support vector machine, SVM)、采用贝叶斯理论的朴素贝叶斯(Naive Bayes, NB)、以及采用压缩感知思想的稀疏贝叶斯学习等[1,4-5]。其中,支持向量机最具吸引力并且被证明是一个强大的信用评估工具[6-7],它基于机器学习理论中结构风险最小化的原则,很多SVM的变型被作为研究对象,其中最小二乘支持向量机(least squares support vector machine, LSSVM)是其典型代表[8-10]。
LSSVM是由J.A.Suykens等[8]提出的对SVM的一个改进。LSSVM利用一组线性方程替代了SVM中的二次规划问题,因此它克服了传统SVM中计算量大的缺陷。核函数类型及其参数是LSSVM中的关键问题,对LSSVM的性能会产生很大影响。传统方法一般采用交叉验证或网格搜索对LSSVM的参数进行优化,前者简单易用,但具有计算密集型和数据密集型的特点;后者通过搜索参数空间来寻找最优参数以达到高性能,它往往优于交叉验证法。然而,因为搜索空间巨大,使得执行寻优策略非常耗时[11]。近年来,出现了一些基于种群策略的优化算法,模拟蜂群分工的人工蜂群(artificial bee colony, ABC)[12]、模拟鸟类觅食的粒子群优化算法(particle swarm optimization, PSO)[13],它们具有很好的数值优化效果,将其用于优化LSSVM中的参数,可获得更好的分类性能。作为一种新近提出的数值优化算法,灰狼优化算法(grey wolf optimization, GWO)被证实在求解精度和稳定性上具有明显优势[14]。但基本的GWO在所有迭代过程中线性调整收敛因子,而未考虑进化过程前后狼群特征的差异;另外,对狼群进化起引导作用的α狼、β狼和δ狼以相同的方式影响ω狼的进化,未有效地区分狼的引领作用。
为了解决上述问题,本文提出一种改进的GWO算法来调整信用评估模型中LSSVM参数的方法。该方法包括2个方面:①引入新的机制来非线性地调整GWO中的收敛因子值,并自适应调整α狼、β狼和δ狼对ω狼的引领方式,改进的算法被称为IGWO;②运用IGWO来调整LSSVM中的重要参数(IGWO-LSSVM),并将其应用到信用评估中。在2个广泛采用的信用数据集上进行了验证,实验结果表明,本文所提出的方法与传统的其他分类器(如KNN、LDA、LRA、DT、NB、SVM和LSSVM)相比,在信用评估中具有更好的效果。
1 相关理论
1.1 灰狼优化算法
狼群具有严格的等级制度和明确的社会分工。S.Mirjalili等提出的灰狼优化算法是一种模拟狼群捕食行为的群体智能算法[14]。其基本思想是将狼群中的狼依据捕食能力分为 α狼、β狼、δ狼和ω狼,其中,α狼起带领作用,β狼和δ狼进行协助(在本文中我们将这3种狼称为引导狼),而ω狼追随,在优化的过程中,α狼始终是具有最优适应度的狼,即最后的最优解。
在每次迭代过程中,灰狼优化算法首先确定α狼、β狼和δ狼,然后用引导狼去更新其余狼的位置信息,其核心步骤可描述为
Dxi= |CiXxi(t) -X(t)|
(1)
Xi=Xxi-AiDxi
(2)
X(t+1) = (X1+X2+X3)/3
(3)
Ai= 2ar1-a
(4)
a=2-2t/tmax
(5)
C=2r2
(6)
其中:i=1,2,3;Xi=α, β, δ;D表示当前狼个体与引导狼之间的距离;t为迭代次数;A为控制灰狼群体全局和局部搜索能力的因子;a为收敛因子,其根据迭代次数t如(5)式线性减小(其中的tmax为最大迭代次数)。当|A|>1时,灰狼群表现为较好的全局搜索能力;而当|A|<1时,其表现为较好的局部搜索能力;r1和r2为[0,1]之间的随机数。
在基本的GWO算法中,收敛因子a线性递减,并未考虑进化前后的差异,理想情况应是在进化前期,a应具有变化较大的值,以使A变化较快而具有更强的全局搜索能力;在后期a应具有变化较小的值,以使A变化较慢而具有更强的局部搜索能力。除此之外,在进行个体狼位置更新时,α狼、β狼和δ狼对个体的影响具有相同的权重,忽视了引导狼的差异,理想情况应是:越优的引导狼对个体狼的影响力越大。因此,传统的GWO算法还有待改进。
1.2 最小二乘支持向量机
基于结构风险最小化原则和VC维理论,Vapnik等人提出了支持向量机SVM,它是一种被广泛用于分类和回归的机器学习算法;而LSSVM是对SVM的改进,其基本思想是采用非线性映射φ(x)将训练样本从低维特征空间映射到高维特征空间中,如此就把低维空间的非线性估计函数转化为高维空间的线性估计函数
y(x) =w·φ(x) +b
(7)
输入训练样本{xi,yi};i=1,2,…,l。其中xi∈Rd是输入向量,其维度为d;yi∈R是输出结果;l代表训练样本数;w、b分别是权值向量和偏置项;而φ(x)为非线性映射函数。
LSSVM将误差平方和定义为损失函数,将SVM的不等式约束二次规划问题变换为线性方程组的求解问题,提高了收敛精度和求解速度。依据结构风险最小化原则,求解(7)式最小的w和b的问题,即求解式(8)表示的最优化问题
(8)
其中:γ为正规化参数;ei为松弛因子。为了求解式(8),引入拉格朗日算子,即可得到式(9)所示的非线性模型
(9)
其中:λi∈Rl×1是拉格朗日乘子;K(·,·)是核函数,其作用是把输入向量从低维空间映射到高维空间。几种常见的核函数如下:
多项式函数
K(x,xi)=[(xi·x)+1]q
(10)
RBF函数
K(x,xi)=exp(-‖x-xi‖2/2σ2)
(11)
Sigmoid函数
K(x,xi)=tanh(ψ(x·xi)+c)
(12)
以上这些核函数中,RBF是最常用的一种。本文所提出的信用评分模型中采用RBF核函数。
2 基于改进的灰狼群优化算法的最小二乘支持向量机的信用评估
2.1 改进的灰狼群优化算法
基本的GWO采用线性减少的收敛因子a来调整狼群的全局和局部搜索能力,理想情况应是在进化前期应具有较大的a来使得变化较快的A来增强灰狼群的全局搜索能力,在进化后期应具有较小的a来使得变化较慢的A来增强灰狼群的局部搜索能力;另外,基本GWO中,引导狼对个体狼具有相同的影响力,理想情况是引导狼越接近最优解,其对个体狼的影响力就越大。基于以上考虑,我们提出了一种改进的灰狼群优化算法(improved grey wolf optimization, IGWO),其改进在于:①提出了一种非线性变化的收敛因子的策略,如式(13)所示;②依据引导狼的适应度值自适应地更新个体狼的位置,如式(14)所示。
(13)
(14)
其中:fxi(xi=α,β,δ)为引导狼的适应度值。相对于传统的线性递减方法,公式(13)描述的收敛因子a在迭代初期,其值从2开始快速下降,使得A变化较快,从而增强灰狼群的全局搜索能力;而到进化后期,a以较慢的速度下降,使得A变化较慢,从而增强灰狼群的局部搜索能力。公式(14)充分考虑了各引导狼对个体狼的影响,引导狼的距离最优解越近,其对个体狼的影响则越大。
2.2 基于改进灰狼群优化算法的最小二乘支持向量机
基于改进灰狼群优化算法的最小二乘支持向量机(IGWO-LSSVM)采用改进灰狼群算法去优化LSSVM中的正则化参数[式(8)中γ]及RBF核中的宽度[式(11)中σ],它们一起构成个体的2个维度,即X=[γσ]。为了评估个体X的好坏,针对信用评估这个典型的分类问题,以错分类比例作为适应度函数的值,即
(15)
其中:S是测试集样本数;Pi和Ti分别是样本预测标签和实际标签。IGWO-LSSVM的目标是最小化该适应度函数的值,算法描述如下。
算法1:IGWO-LSSVM
输入:N(灰狼群大小);tmax(最大进化代数);γmin、γmax(γ的最小值、最大值);σmin、σmax(σ的最小值、最大值)。
输出:最优γ,σ。
步骤一:生成具有N个个体的初始种群,每个个体是一个二维数据[γσ];
步骤二:根据适应度函数(15)评价每个个体,更新α狼、β狼和δ狼;
步骤三:根据公式(13)、(14)更新个体狼的收敛因子及位置信息;
步骤四:如果达到最大进化代数,停止算法并输出最优值,即α狼的位置。否则,执行步骤二。
算法1的主要特点是能非线性调整收敛因子的值及根据引导狼的适应度值自适应地调整个体狼的位置信息。
2.3 基于IGWO-LSSVM的信用评估
基于IGWO-LSSVM的信用评估模型的步骤包括:数据预处理、数据集划分、模型构建和模型评价[15]。算法具体描述如下。
算法2:基于IGWO-LSSVM的信用评估
输入:算法1中的输入参数,信用数据,K交叉验证数据划分组数。
输出:评价指标。
步骤一:对信用数据进行归一化处理;
步骤二:将数据划分成2个部分:训练集和测试集;
步骤三:确定LSSVM的核函数的类型并应用IGWO-LSSVM对参数进行选优;
步骤四:将步骤三得到的优化结果作为LSSVM的参数,在训练集上构建信用评估模型;
步骤五:在测试集上评估模型。
算法2的核心思想是利用优化后的值作为LSSVM中γ和σ参数值,以达到更好的信用评估效果。
3 实验分析
3.1 评估模型的指标
信用评估模型的混淆矩阵如表1所示。

表1 信用评估混淆矩阵Table 1 Credit assessment for confusion matrix
基于混淆矩阵,很容易算出如下指标

(16)

(17)

(18)
其中:正确度代表模型所有正确分类的客户数与数据集总数的百分比;敏感度是指正确分类的好客户占所有好客户的百分比;而特异度则是指正确分类的坏客户占所有坏客户的百分比。分别以特异度和敏感度为横、纵坐标轴,就得到接受者操作特征曲线(ROC),该曲线下面积就是AUC的值。AUC取值为(0.5, 1],模型分类性能越好,该值就越大[16]。
3.2 实验数据集
为了验证本文提出的评估模型,选取了加州大学欧文分校(UCI)提供的2个公开信用数据集——澳大利亚数据集和德国数据集,这2个数据集的基本信息如表2所示。

表2 信用数据集基本信息Table 2 Basic information of credit data set
澳大利亚数据集总共包含客户信息690个,坏客户307个、好客户383个,客户信息均由6个离散型属性及8个连续型属性组成。德国数据集包含300个坏客户和700个好客户,客户信息由13个连续型属性和7个离散型属性共同描述;由于数据的保密性,所有的属性名都用符号表示。该数据集中存在5%(37个)的样本有一个或多个缺失值,针对离散型属性缺失值,选用同类样本在此属性上出现的最高的频率值来代替;而对于连续型属性缺失,用同类样本在此属性上的平均值代替缺失值。
3.3 实验设置
本文提出的IGWO-LSSVM模型分别与传统信用评估方法进行对比,以此验证IGWO-LSSVM模型在信用评估中的效果。这些传统方法包括LDA、LRA、KNN(N=9)、DT(ID3)、SVM和基于网格的LSSVM(GLSSVM),所有变量采用线性映射规范化到[0,1]区间。对于LDA、LRA、DT、KNN和NB,采用Matlab 2013a提供的工具箱,所有方法无参数或采用默认参数;对于SVM,采用默认参数的线性核LibSVM[17];对于GLSSVM,采用RBF核函数,其查找空间为γ=2i(i=-14, -13,…, 6, 7)和δ=2j(j=-7, -6, …, 6, 7)。
所有实验在3.40 GHz i7-3770 CPU、16 G 内存、Windows7 64位操作系统上执行,IGWO-LSSVM所采用的参数如表3所示。
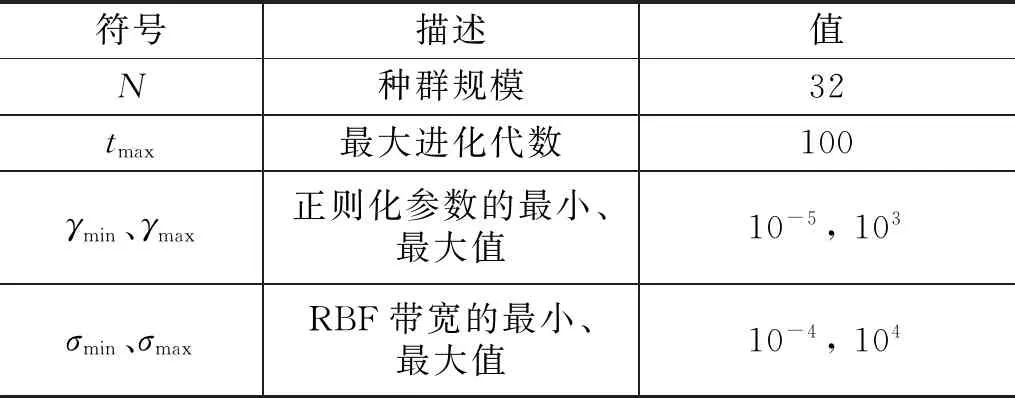
表3 参数设置Table 3 Parameter settings
3.4 实验结果
为了减少数据对实验的影响,实验重复了20次,每次执行5折交叉验证操作。报告的是各项指标在这20次运行中的平均值及标准差(方括号内为标准差)。
3.4.1 德国数据集
在德国数据集上的结果如表4所示,IGWO-LSSVM取得了最高的正确度、敏感度和AUC。具体来说,对于正确度,IGWO-LSSVM取得了最高值79.28%,远高于DT、KNN和NB,而LDA、LRA、SVM和GLSSVM取得了比较高并且很接近的值;同时,IGWO-LSSVM的标准差0.43也是最小的,表明IGWO-LSSVM最稳定。类似的结果还体现在AUC中,IGWO-LSSVM取得了最高(80.33%)并且最稳定的AUC;IGWO-LSSVM的敏感度(90.74%)在所有方法中也是最高的;对于特异度,IGWO-LSSVM取得了第二高的值,最高值由NB取得。

表4 德国数据集结果Table 4 German dataset results
3.4.2 澳大利亚数据集
在澳大利亚数据集上的结果如表5所示。相对于其他方法,IGWO-LSSVM取得了最高的正确度和AUC。具体来说,对于正确度,IGWO-LSSVM取得了最高值87.48%,远高于其他方法;IGWO-LSSVM的敏感度仍然是最高的,略高于NB。
从表4和表5可以看出,本文提出的IGWO-LSSVM具有最好的信用评估性能,在2个数据集上,相对于LDA、LRA、KNN、DT、NB、SVM和GLSSVM,IGWO-LSSVM的分类正确度平均提高了2.3%、2.0%、5.9%、9.5%、9.0%、2.9%和2.2%。这些数据表明,IGWO-LSSVM是一种有效的信用评估方法。同时,IGWO-LSSVM相对于GLSSVM的信用评估性能的提升,表明IGWO方法是一种有效的参数优化方法。

表5 澳大利亚数据集结果Table 5 Australian dataset results
4 结束语
本文提出了一种改进的灰狼优化算法IGWO,并将该算法用于优化LSSVM的2个重要参数,然后将LSSVM用于信用评估中。实验表明,在信用评估中,所提出的IGWO-LSSVM方法在分类正确度和AUC两个方面具有明显的优势,能大幅度提高信用评估性能。进一步将研究GWO的其他自适应方法,基于LSSVM的组合分类器及其在信用评估中的应用。
