瞬变电磁过套管电阻率测井响应模拟及分析

沈建国,谭刚,朱留方,臧德福,张付明,黄玉科

(1.天津大学微电子学院,天津300072;2.中石化胜利石油工程有限公司测井公司,山东东营257096)

0 引 言

传统的过套管电阻率测井是直流方法,受套管影响大[1],电流主要沿套管流动,受接触影响大,对井眼条件要求高。本文采用线圈电流导通和关断方式激发大功率瞬变电磁场,发射和接收线圈不与套管接触[2],通过电磁感应,使瞬态的低频电磁能量穿过套管,在地层中形成瞬态涡流,该涡流在套管井内再次激发瞬态电磁感应响应[3-5],测量该响应的波形得到地层电导率[6-7]。具体测量时采用不同源距进行接收。与直流方法不同,瞬变激发的电磁场频谱连续,包含丰富的频率成分,低频幅度较大,高频幅度较小[8],其响应是瞬态波形,地层电导率信息通过瞬态波形携带。

过套管瞬变电磁测井是全空间问题,其响应与地面瞬变电磁均匀半无限大空间有比较大的差别,主要表现为半无限大的空气介质(传播电磁波)变成了有限的井孔圆柱(形状),无限大平面边界变成了套管内边界。井周围的钢管是高电导率和磁导率介质,对套管内线圈激发的瞬变电磁场衰减大。在套管内接收,其幅度随源距快速衰减。文献[8-10]建立了理论模型并进行了实验研究,所得到的响应波形是单调减小的,类似于地面瞬变电磁的近偏移距响应。其地层电阻率处理也类似于地面瞬变电磁,在单调衰减的响应波形上取n个时刻的幅度值构成n条测井曲线，经过刻度后得到地层电导率测井曲线。该方法在套管损伤检测方面取得了成功，在套管变形或者腐蚀的深度,n条曲线都有明显的变化。但是，对地层电阻率测量时，因为地层电导率所引起的有用信号幅度很小，处理难度比较大。

本文用实轴积分方法(频谱法)研究套管井中不同源距的瞬变电磁响应。结合微分方程分析了2种响应,因为频率低、集肤深度大,套管对电磁能量的屏蔽比较弱,满足Doll电磁感应原理,以此为基础讨论了无用信号的消除方法和地层电导率处理方法,得到了套管井地层电导率变化曲线。

1 现场实测波形

实验仪器不用贴井壁,采用了一发四收线圈同轴安装在一起构成一个圆柱体,4个不同源距的接收线圈R1、R2、R3和R4的源距为L1=0.275 m,L2=0.43 m,L3=0.6 m,L4=0.77 m。在5.5 in[注]非法定计量单位,1 in=25.4 mm,下同的套管井中接收到的4个波形形状差异比较大(见图1)。其中,发射波形的激发逻辑:延迟60 ms、正向导通60 ms,关断60 ms,反向导通60 ms,关断160 ms。在1个激发周期中,有2次导通和2次关断过程。这4个时刻,发射线圈中的电流快速变化,在地层和套管井中激发出比较强的瞬变电磁场。4次激发的瞬变电磁场均有相应的瞬态响应,合在一起构成原始测井波形。

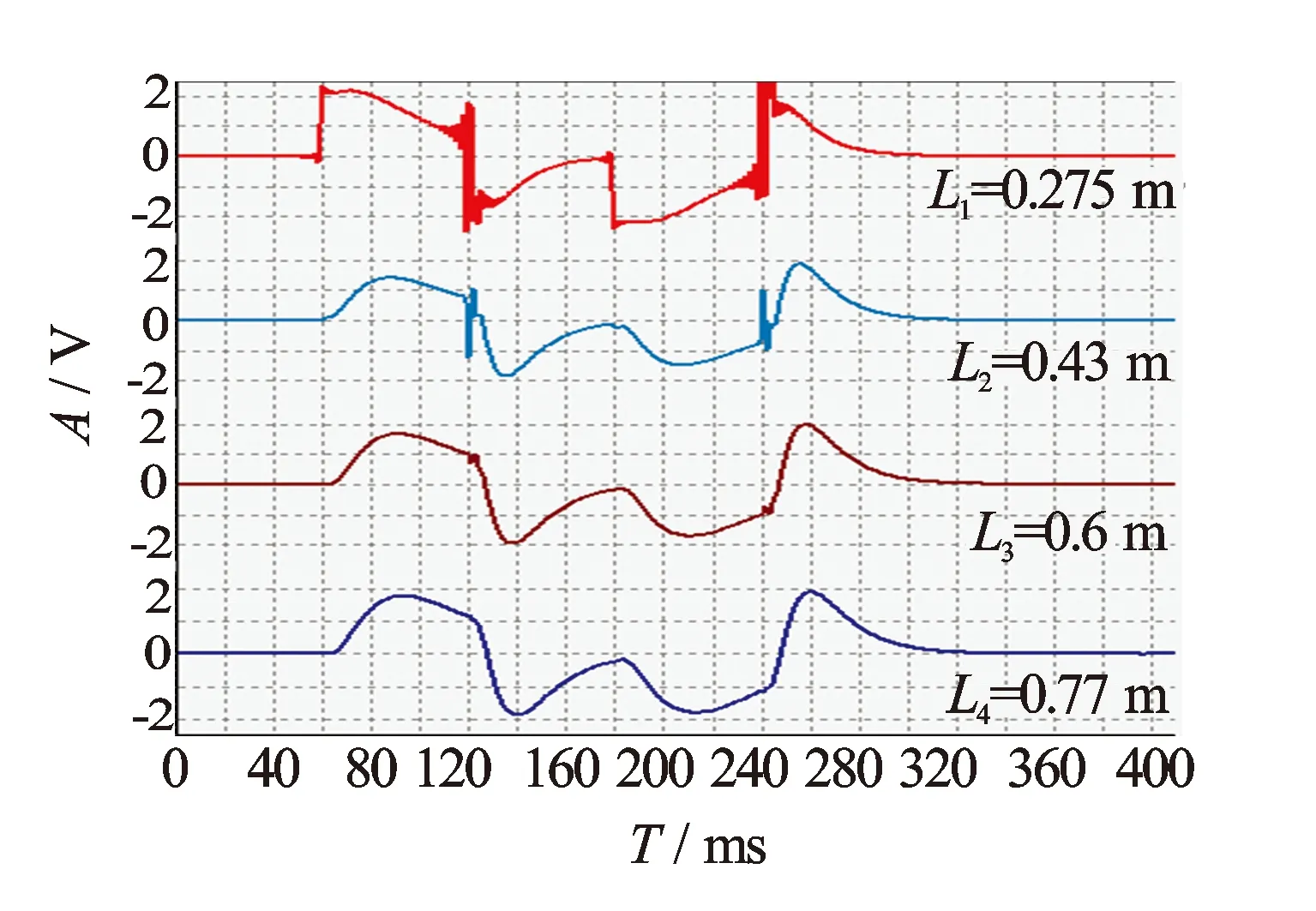
图1 4个源距的原始测井波形(5.5 in*套管)

将4个波形重叠绘制得到图2。从图2可以看出,最近源距的波形在导通或者关断时刻出现阶跃响应,瞬间达到很大的值,其他源距的3个波形则慢慢地增加,达到极值以后幅度开始减小,随着源距增加,波形的极值明显地向后移动,这说明电磁能量在套管井内具有一定的传播特征。但是,与声波的传播不同,响应波形形状随源距变化,不同源距的响应波形形状不一样。

图2 4个源距的原始测井波形

从图1和图2还可以看到,正向导通(60 ms位置)即发射线圈电流导通瞬间,图1最上面响应波形即图2的蓝线出现从0～2.3 V的正向阶跃,并伴随有高频震荡,之后,响应开始慢速上升到极大值,随之开始慢速下降并趋于舒缓。在关断时刻(120 ms位置)则出现反方向(正0.7～-2 V)突变,并伴随着剧烈震荡,开始平滑地增加,最后接近于0。反向导通和关断时响应也突变,其极性与正向导通、关断相反,响应震荡也非常剧烈。这是近源距的响应特征,与地面瞬变电磁源距的响应有区别:0源距的响应是导通瞬间达到极值,之后幅度单调减小。近源距的波形对激发线圈的导通和关断时刻非常敏感,可以直接显示激发时刻。

源距增加以后,关断时刻的响应变成尖峰,并且随着源距增加,尖峰幅度逐渐减小并最终消失。在图1中,从上到下的第2个波形能够看到明显的尖峰,第3个波形的尖峰幅度很小,第4个波形则完全看不到尖峰了。即该响应随着源距增加,幅度快速衰减,并最终消失。

除了尖峰外,其他时刻的响应波形均连续变化,其特点是先快速变化,达到极值以后慢速变化。源距增加,变化减慢,极值依次向后移动。

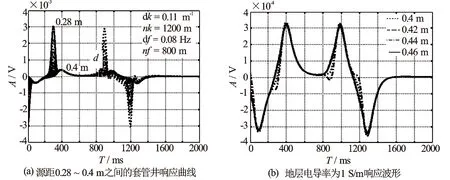
图3 不同源距的响应波形

2 响应波形的数值模拟

为理解上述实测波形特征,本文建立套管井模型进行数值模拟。用轴向无限长、径向4层介质(沿径向半径向外依次是井内液体、套管、水泥环、地层)构建套管井模型,选择柱坐标系,井轴与z轴重合。

用分离变量法求解,套管井内的响应为

C(kz,ω)I1(l1r)]ei(kzz-ω t)dkzdω

(1)

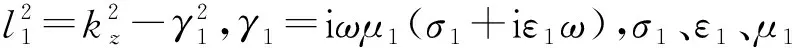
选择8.5 in井眼,5.5 in套管井进行计算,kz=2πk,k离散化,取步长dk为0.1,(见图3中的dk=0.11/m),个数nk为1 200,k最大计算到120,ω=2πf,f离散化,取步长df为0.08 Hz(见图3中的df=0.08 Hz),频率个数nf为800,f最大计算到64 Hz。井内液体的电阻率为0.5 Ω·m,套管的电导率为8×108S/m,水泥环电导率为1/20 S/m,地层的电导率为1 S/m。井内液体和套管的相对介电常数为50,水泥环和地层为1,井内液体、水泥环和地层的相对磁导率为1,套管为2 000。

图3所示为不同源距的响应波形。图3(a)的源距是0.28～0.4 m,4个大的尖峰位置分别对应于正向导通(0时刻)、正向关断(300 ms)、反向导通(900 ms)和反向关断(1 200 ms)时刻。0.28 m源距的波形尖峰幅度最大,源距增加到0.4 m时,尖峰消失[见图3(b)],只有变化比较慢的响应,与源距大于0.43 m后所测量的波形(见图2下面的波形)形状相似。由于计算时最大频率只取到64 Hz,瞬变激发的高频成分没有计算,所以,尖峰没有实际测量的尖锐。

无限大均匀导电介质的瞬变电磁响应有位移电流(与介电常数ε和磁导率μ有关)和传导电流(与电导率σ和磁导率μ有关)2个部分,冲击函数激发[4]时其对应的解中有冲击函数和解析函数,其中,冲击函数对应于电磁波的解,解析函数对应于电磁感应的解。高频时位移电流的响应幅度比较大,响应以电磁波为主;低频时传导电流的响应幅度比较大,以电磁感应响应为主,传统的感应测井理论[1]通常不考虑电磁波传播,忽略介电常数的影响,只研究电导率所引起的响应。

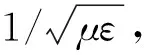
(2)

式中,Hy为y方向的磁场强度;t为时间;2是拉普拉斯算符。右端第1项是位移电流,描述电磁波;第2项是传导电流,描述电磁感应和电磁能量在导电介质中的传播和衰减特征。

套管本身是高电导率和磁导率介质,仪器在套管井中测量时,套管对其中间的空气或水中的电磁波和电磁感应衰减均比较大。套管直径不同,套管中间的空气或者水的圆柱体积不同,所得到的响应也明显不同。图4是7 in直径的套管井内测量的波形,与图1对比发现,导通和关断时刻的振荡响应幅度均有所增加,在4个源距的波形中都能够看到其振荡变化。其他时刻的幅度变化:第1个波形的幅度在导通时刻以后很大,超出最大采样幅度2.5 V,关断时刻以后的幅度变小,其他源距波形的幅度均有所减小。

图4 4个源距的原始测井波形(7 in套管)

电磁波的传播速度非常快,在现有的源距中其延迟可以忽略不计,因此,出现在激发瞬间[见图1、图4(120 ms和240 ms位置)],由式(2)可知,其传播速度与介质的磁导率和介电常数有关,与电导率无关,因此过套管电阻率测井不需要关注。

第2个响应是传导电流的响应,即通常的电磁感应响应,与地层的电导率和磁导率有关,是式(2)第2项,对时间的一次导数,描述电磁场的衰减:电导率越大,响应幅度随源距衰减越快、随时间衰减越慢。现有的瞬变电磁勘探和瞬变电磁测井[8]均依据源距或者近源距的响应:随时间衰减,用不同时刻的响应幅度确定地层的电导率[2,4-5,7]。本文则依据不同源距的电磁感应响应确定地层的电导率。

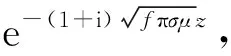
3 过套管电阻率测量

套管井内的4种介质(井内液体、套管、水泥环和地层)均导电。瞬变电磁在4种介质中激发的响应均是随时间变化的。由于集肤深度比较深,总的响应满足Doll的近似条件,可以用电磁感应原理进行分析。每种介质的响应(感应电动势)均会在其中产生涡流,该涡流会再次在接收线圈激发电磁感应信号,Doll称其为二次场(有别于地面瞬变电磁勘探记录的发射电流关断以后测量到的信号,地面勘探测量的二次场相当于本文的传导电流的响应),该信号与介质的电导率成正比。在套管井内套管、水泥环和井内液体均能够产生二次场信号。这些二次场信号对于过套管电阻率测井来讲是无用信号,需要消除,只有地层的二次场信号与地层的电导率成正比,才是有用信号,用于获得地层的电导率。

本文数值模拟所得到的瞬变电磁响应是井内液体、套管、水泥环和地层构成的4层圆柱形介质模型的综合响应。由于瞬变激发信号的频谱(1/f)以低频为主,介质的介电常数影响小,电导率对响应起决定作用。因为主频比感应测井的频率20 kHz低很多,响应中地层的二次场信号(有用信号)远远小于无用信号,图1、2所示的原始测量波形主要是无用信号,在测井过程中基本上保持不变,或者说地层电导率改变引起的波形变化很小,直观上基本看不到。只有当仪器经过套管节箍时,响应波形才有明显地变化。这是因为节箍处的套管厚度变大,导磁和导电(108)介质增加所导致的。高电导率和磁导率套管的厚度变化对响应影响很大。

套管比较薄,夹在井内液体和水泥环之间、外面是无限大的地层,电导率比地层和水泥环大,其影响通过边界条件表现:使响应波形的形状变缓(套管对高频成分强烈衰减)、幅度随z快速衰减,不同源距的套管井波形与裸眼井或无限大均匀地层的响应波形形状差异大。对于瞬变激发的低频成分,套管的集肤深度大,电磁能量能够穿过薄的套管进入地层,在地层中激发涡流,涡流穿过套管在接收线圈上能够再次激发电磁感应响应。

Doll几何因子没有考虑圆柱边界的影响,因此,不能够简单地用于含套管的二次场计算。但是,Doll提出的涡流再次激发的二次场可以用于瞬变电磁响应的分析。

从测量的瞬态波形中去掉无用信号仅剩下地层的二次场是原始波形处理的关键。本文用同一源距在不同位置测量的波形相减去掉无用信号。因为同一源距的响应波形形状一致,波形中所包含的井内液体、套管和水泥环的响应也基本相同(套管不变形),不同深度所测量的地层不同,地层的电导率不一样,两者相减所得到的波形中不再包含井内液体、套管和水泥环的影响,只有地层不同所引起的二次场差。如果相减的2个地层电导率一致,则波形为0。2个波形相减以后仍然是一个瞬态波形,该波形的每一点幅度都反应地层的电导率,可以用(类似Doll)几何因子进行描述。波形幅度越大,对地层电导率测量的灵敏度越高。一个激发周期内有正、反向导通和正、反向关断4次激发,相应地有4个时刻二次场最强,取得极值,该极值最能够反应所测量地层的电导率,对其刻度并加上初值(被减波形对应的电导率值)便得到地层的电导率。

为了减小套管变形或者腐蚀的影响,用相邻深度测量波形相减。这时所测量的位置相近,套管的影响基本一致,相减以后所得到的波形消除了套管的影响。如果地层比较厚,则所测量的波形差异为0,当地层厚度小于一定值时,2个测量点所测量区域内地层电导率有差别,则波形相减后不为0。

对图2所示的测量波形,用相邻2个深度点测量波形相减(去掉无用信号)的方法处理得到图5所示的波形,其与相邻2个测量点所测量区域内地层电导率有关,称其为地层电导率信息分布图。共有4个图像对应于4个源距的波形,从上到下源距依次增加,其横坐标是地层深度,纵坐标是时间,颜色表示测量到的瞬态波形相减后的幅度差(每个激发周期采集400个点)。每个激发周期所测量的波形中(400点)包含4次瞬变电磁激发(4次导通、4次关断),原始测量的地层电导率信息集中分布在这4个时间区域,见图5中颜色比较突出的4个区域,其中,2个分布为正,另外2个分布为负,极性相反。图5中颜色比较深的竖直区域(长)部分是套管节箍,每相隔大约9 m出现一次。

从图5可见,套管节箍处的电导率差异最明显,因为有双层套管,等效电导率大。在套管节箍之间,黄蓝相间的区域是相邻地层的电导率差异引起的二次场变化,越黄表示二次场差的正向越大,越蓝表示二次场差的负向越大,绿色表示没有差异。4个源距探头所测量的二次场差分布有一定的差别。

图5 相邻2个深度点的测量波形相减得到的地层电导率信息分布

以上结果是最直接的原始地层电导率信息测量结果,4个分布源距不同,直观地显示了套管外不同深度地层的电导率的差异。

4 电阻率曲线

将上述方法处理的地层电导率信息分布转换为测井常用的地层电导率曲线,需要借助于几何因子。从图5所示的波形中选择一个幅度变化比较大的时刻(一共有4个,分别对应于2次导通和2次关断时刻之后一段时间),将其幅度取出,得到1条曲线,依据Doll电磁感应原理,该曲线是该相邻深度点附近地层电导率加权(几何因子)以后(响应)的差。每个测量点的响应均对应于一个几何因子,描述该点附近的地层电导率对响应的贡献,同一地层在不同测量位置的响应中权重不一样。相邻2个深度点的响应相减实际上相当于这2个测量点的几何因子相减,所得到的响应曲线可以用相邻2点的几何因子相减描述。这里先用Doll几何因子对曲线进行定性分析。

图6 电磁感应的Doll几何因子

图6是Doll几何因子,图7是2个相邻深度点响应相减以后所得到的响应差的几何因子,它是2个相同的几何因子(见图6)其中一个移动一个深度间隔以后与另外一个相减所得到的。分别有2个正峰、2个负峰。取不同的半径r得到几何因子随z的变化规律(见图8),半径小,几何因子的正、负峰分别有2个,半径增加以后,只有1个正峰、1个负峰。取定井半径,计算一定径向深度地层总的几何因子得到图9所示随z的变化规律。这些规律刻画了响应差随深度的变化,即图5所示不同时刻的响应差随z的变化形状,这些形状在测井过程中通过地层界面表现出来。因为当仪器遇到水平界面时,不同测量点相对于水平界面的距离不同,每个测量点所测量的区域内地层电导率有差异,响应差不同,发射或接收线圈经过界面时,响应差均会按照图9所示的形状出现正峰和负峰,构成图5所示的图像分布。套管井条件下,套管的高电导率和磁导率将改变瞬变电磁响应分布。套管的响应幅度大,根据电磁场的连续性,套管外(与套管连接的)地层其电磁场也很强,幅度也大,产生的涡流大,在接收线圈中激发的二次场感应信号强。随着半径增加,离开套管的距离增加,其地层的电磁场幅度快速减小,响应幅度也快速单调减小,地层涡流也单调减小,所产生的二次场也单调减小,使得套管井主要测量套管外附近地层的电导率,探测深度比较浅,其对应的几何因子形状与Doll几何因子有一定的差异。

图7 相邻深度点响应相减以后的其响应差的几何因子

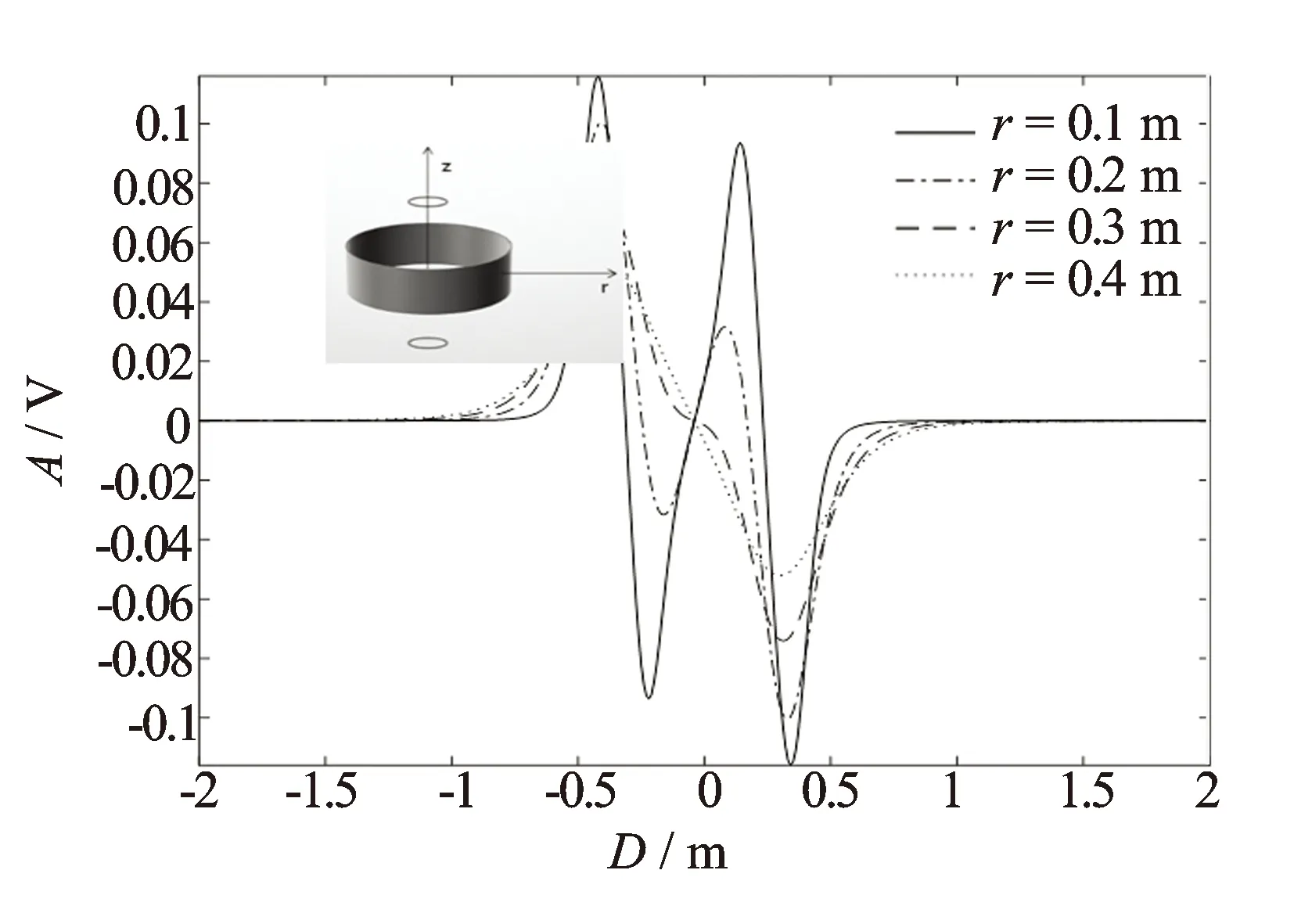
图8 相邻深度点响应相减后其几何因子在半径r取不同值时随z的变化规律

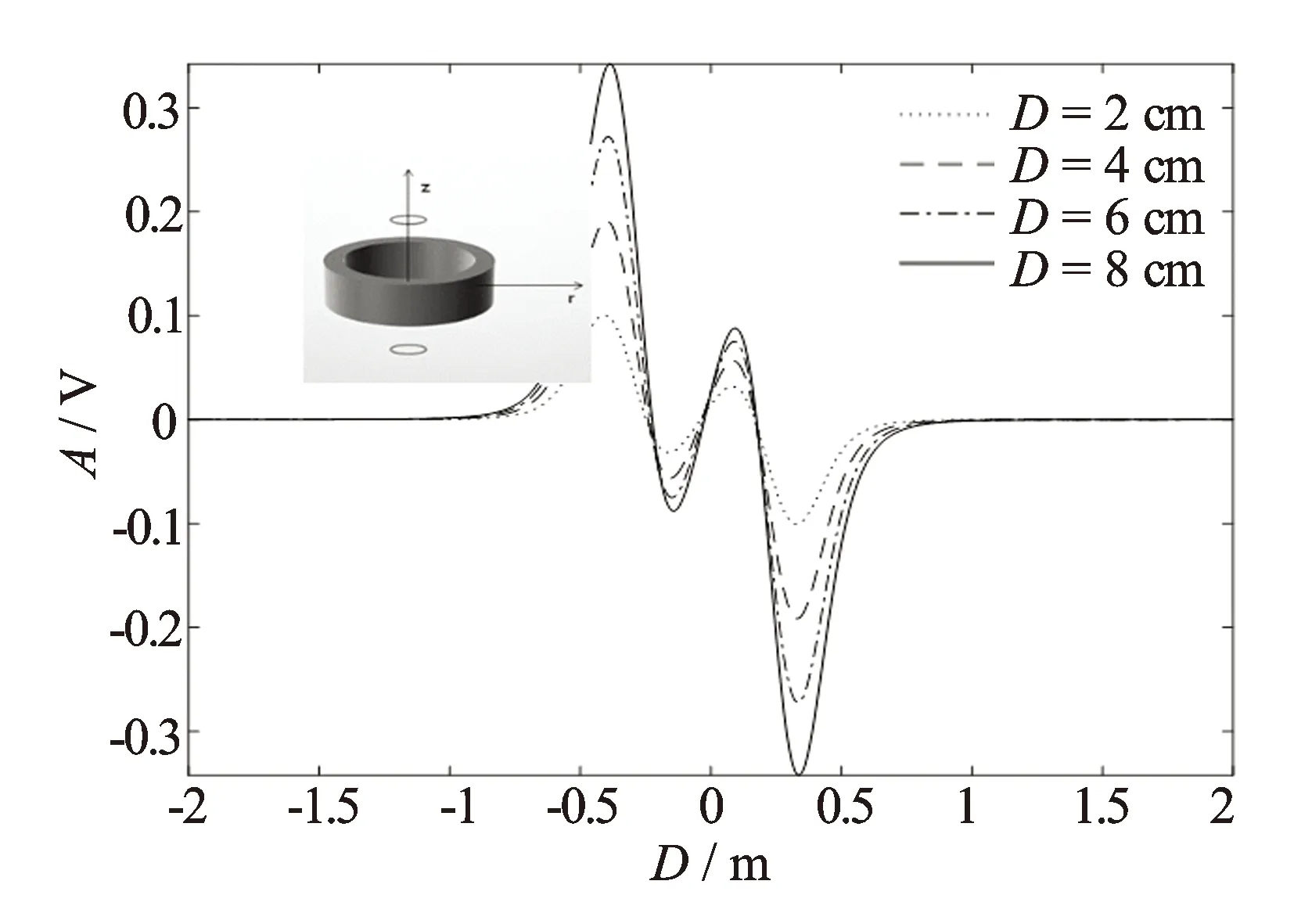
图9 相邻深度点响应相减以后其几何因子在径向一定深度积分以后的结果

将相同源距相邻深度点的测量波形相减,从中取固定时刻的幅度值得到1条曲线,对该曲线进行反褶积处理得到连续曲线,该曲线与地层电导率成正比,直接反映了所测量地层的电导率随深度的变化规律,经过刻度并加上初值即得到地层的电导率。图10是用第4个实际测量波形处理的电导率变化曲线与同时测量的GR对比,图10中套管节箍的影响比较大,在每个节箍处均有一个大的跳跃。

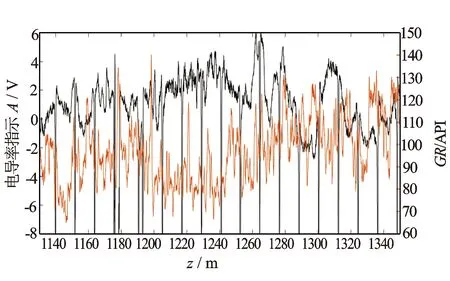
图10 用第4个波形处理的地层电导率变化曲线与GR对比

5 结 论

(1)用瞬变电磁激发,不同源距测量时,在套管井中能够同时记录到位移电流和传导电流分别引起的2个响应。位移电流的响应是脉冲,位于激发时刻,幅度随源距快速衰减。在5.5 in套管井内测量时,0.6 m源距的波形中能够观察到该脉冲;套管直径增大到7 in时,在0.77 m源距的波形中也能够观测到。该响应与地层电导率无关,不是瞬变电磁测井关注的重点。

(2)传导电流引起的响应是一个连续的缓慢变化的波形,开始变化快,达到峰值以后慢速变化,拖尾比较长,其幅度与地层电导率有关。但是,地层电导率在其中所占的比例很小,在测井过程中几乎看不出波形幅度的变化。用相邻2个深度点测量波形相减可以去掉无用信号,所得到的有用信号的波形幅度随地层变化明显,在正、反向导通和关断附近幅度都比较大。

(3)任意取一个时刻的幅度可以得到1条曲线,该曲线可以用相邻2个深度点的几何因子相减描述,对其进行反褶积便得到连续的与地层电导率成正比的曲线。该曲线乘以比例因子便反映了套管井条件下地层电导率随深度的变化规律,与实际地层的电导率相差一个初值。