水射流冲埋砂质海床土体数值模拟

池 寅， 时豫川, 吴海洋, 苏 洁, 余 敏， 卢秋如

(1.武汉大学 土木建筑工程学院，武汉 430072；2.中国电力工程顾问集团中南电力设计院有限公司，武汉 430071；3.武汉工程科技学院，武汉 430223)

随着我国岛屿间电力网络的完善、通信需求的增大以及国际间信息传输交流的迅猛发展，我国海底电缆的数量日益增加。然而，海底环境的复杂性、渔船日常作业和人为锚害等因素对其安全运行造成了很大的威胁，因此电缆管道的安全敷设非常必要。目前主要的海底电缆保护措施是深埋[1]，需要对海床开沟埋管，最常用的埋设方法是冲射法[2]。但由于海床土体的不透明性，冲埋过程的瞬时性等因素的限制，水射流冲埋海床土体的内在机制仍不清楚。此外，冲埋设备及其性能选择的不合理可能导致冲埋施工时的冲埋效果较差，甚至需要二次冲埋，增加工程造价。因此，研究水射流对海床土体的冲埋过程具有一定的理论意义和工程价值。

数值模拟已成为研究水射流的重要手段。常用的数值仿真方法有有限元法(Finite Element Method, FEM)、光滑粒子流体动力学法(Smoothed Particle Hydrodynamics, SPH)和ALE(Albitrary Lagrange-Euler)流-固耦合法等。林晓东等[3]基于SPH耦合FEM的方法模拟了磨料水射流破岩过程，并结合模拟结果分析了磨料浓度30%的磨料水射流在不同速度作用下岩石的损伤范围。Ma等[4]基于FEM耦合SPH法，建立了高压纯水射流冲蚀低碳钢的模型，得出了水射流的速度与最大冲蚀深度的关系曲线，并与试验结果进行对比验证，验证了该仿真方法的可行性。刘佳亮等[5]基于ALE算法，建立了高压水射流冲击高围压岩石的数值模型，分析了冲击过程中的损伤演化。通过对比不同水射流速度下的损伤演化过程并从理论上得出提高射流速度能明显提高射流破岩效率的结论。然而，现阶段对于水射流的研究主要集中在冲击岩体、金属以及煤体等介质，水射流冲埋海床土体方面缺乏相关的数值模拟研究。

本文采用SPH-FEM耦合算法对水射流冲埋砂质海床的过程进行数值仿真计算，分析冲埋过程中海床土体的应力波特性及喷射压力和海床土体物理力学指标对水射流冲埋速率的影响规律。通过对数值模拟结果进行拟合，得到冲埋深度与时间的关系式，可作为不同海床土体条件下选择合适喷射压力的参考。

1 计算模型描述

为了对问题进行一定的简化，在建模前作如下假定：①在冲埋设备平稳行进过程中，其底部水射流在冲埋过程中冲击角度不发生改变；②实际冲埋过程中，水射流的重力与周围海水对其的浮力是一对平衡力，因此不考虑水射流自重对冲埋深度的影响；③电缆铺设与水射流冲沟同时进行，可忽略土体在自重的影响下回填而影响冲埋深度；④水射流由水下冲埋设备底部发出，离海床土体很近，因此可忽略水射流在海洋环境中的冲击能量损失；⑤由于实际冲埋过程中水刀长度远大于其宽度，因此可认为沿着水射流水刀厚度方向各截面处应变相同，而沿着水刀长度方向应变可忽略不计，从而将三维空间问题转化为二维平面应变问题。

1.1 几何模型

1.1.1 水射流模型

采用SPH法建立水射流模型。设置水刀的宽度为20 mm，选择较大的高度值用来实现实际冲埋过程中水射流的不间断冲击。

1.1.2 土体模型

在建立土体模型时，将与水射流接触部分及附近区域可能产生大变形的土体处理成SPH粒子。对远场应力较小区域的土体则采用FEM法建模。两部分海床土体通过接触算法进行连接。综合考虑实际工作参数及仿真效率，建立的砂质海床土体模型宽1 000 mm、高1 500 mm，其中SPH土体宽500 mm、高1 500 mm。整体2D模型如图1所示。

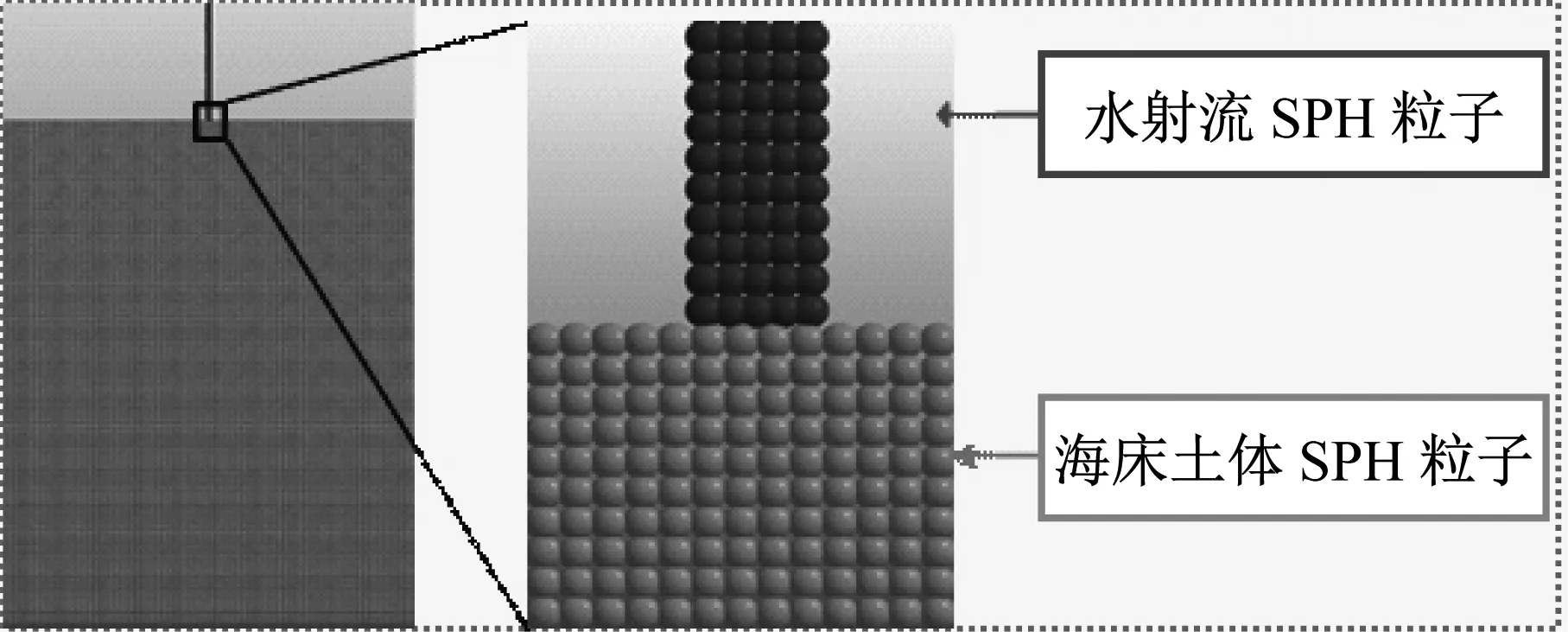
图1 水射流与海床土体2D模型

1.2 材料模型

1.2.1 土体

海床土体分别为松散细砂，中密细砂，密实细砂，中密粗砂以及中密粉土五种砂质土体材料，材料的相关物理与力学参数根据调研资料以及试验得到，列于表1。定义材料模型为MAT_FHWA_SOIL土体本构模型。土体处于动荷载作用下且涉及运动和大变形问题，因此假定弹性阶段弹性模量与压缩模量一致，即E=Es。根据Trautmann等[6]对砂质海床土体取泊松比v=0.3。为模拟孔隙水压力的作用，定义体积模量是关于无孔隙体积模量、孔隙度及饱和度的函数

(1)

式中：Ki为固结土体的体积模量；ncur为孔隙率；D1为控制孔隙坍塌前土体刚度的材料常数。采用Abbo等[7]提出的修正Mohr-Coulomb屈服准则，屈服面F为

ccosφ=0

(2)

式中：参数ahyp用来表征修正后的Mohr-Coulomb屈服面与标准的Mohr-Coulomb屈服面之间的拟合程度。参数ahyp应接近于零，但需始终满足如下公式

ahyp=0.05ccotφ

(3)

将标准Mohr-Coulomb屈服面的偏平面形状函数G改为Klisinski等[8]所使用的函数

G(θ)=

(4)

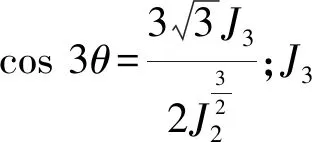
定义土体的内摩擦角是关于有效塑性应变的函数来反映应变硬化特性。为模拟应变软化特性，模型采用Ju[9]提出的连续损伤算法。具体的五种不同砂质海床土体材料的本构参数，如表2～表4所示。

表1 砂质土体的物理力学指标及参数

表2 砂质土体材料相关本构参数

表3 砂质土体材相关本构参数

表4 砂质土体材料相关本构参数

1.2.2 水射流

采用LS-DYNA中的MAT_NULL材料模型，对水射流材料模型赋予Mie-Gruneisen状态方程[10](式5)。

(γ0+aμ)E

(5)

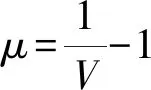
(6)

水射流材料模型的主要参数如表5所示。

表5 水射流材料参数

1.3 边界条件

对土体模型采用无反射边界条件，用以模拟海洋中无限远场的海床土体，同时能够防止在边界产生的人工应力波反射重新进入模型从而干扰数值计算结果。对水射流模型采用速度边界。

2 计算结果分析

2.1 冲埋过程的应力波特性

图2为水射流速度为30 m/s的情况下，海床土体与水射流接触面及截面内部的应力波形成及传播过程图。1 ms时刻，在土体与水射流接触面至40 mm深度区域内产生应力集中，应力最大值在水射流中心线与海床土体表面接触点处。应力集中区域随时间的增加不断扩大。3 ms时刻，应力波在海床土体内部沿水射流中心线方向初步形成。之后，应力波不断向海床土体底部及四周传播，使得土体在应力波的反射拉伸作用下发生拉伸损伤，应力最大值点仍保持在水射流中心线与海床土体表面接触点处，因此水射流冲击海床土体总是沿着中心线成坑。

图2 海床土体内部应力波形成及传播过程

选取水射流中心线与海床土体表面接触点处的单元为A点，并沿水射流中心线向海床底部等距离选取7个单元(编号B～H)，绘制该8个单元的MISES应力-时程全曲线(见图3)。由图3可知：A点的应力值在水射流与海床土体接触时迅速增大，形成应力波时达到稳定； B～H单元的应力值由于应力波的扩散呈现出先上升后下降的趋势，且在应力波周期内，海床土体内部沿着射流中心线方向上各点的应力值基本满足BCDEFGH的关系，体现了应力波的不断衰减。

2.2 冲埋速率影响因素分析

2.2.1 喷射压力

为了凸显喷射压力对冲埋速率的影响，分别选取水射流速度为200、400、60 m/s，根据温赞江[11]提出的水射流速度与喷射压力的关系式(式7)，可得对应的水射流喷射压力分别为0.2 MPa、0.8 MPa和1.8 MPa。土体选用松散细砂质海床土体。

(7)

图4为3种喷射压力条件下不同时刻的冲埋成坑形貌对比图。当喷射压力为0.2 MPa时，水射流碰撞砂土后随即发生侧向溅射，由于侧向飞溅的水射流粒子能量低，使得海床土体SPH颗粒被剥离速度很缓慢，导致冲埋速率非常低下。而当喷射压力为1.8 MPa时，水射流SPH粒子在碰撞海床土体后快速贯入其内部。随着水射流的不断冲击，海床土体在竖向及侧向损伤迅速增大，孔洞深度与宽度都在扩大，而侧向飞溅的水射流粒子由于受到土体边壁约束而改变运动轨迹对孔洞进行反向冲刷，导致海床土体演化为“火山口”的形状。

布莱德先生慢慢地说：“死亡是需要学习的。临死的时候，很多人不知所措。没有人教授这种知识。当死亡来临时，人们一无所知。我们就是要帮助大家，当然，也是在帮助我们自己。只有懂得生命的意义的人，才有勇气探讨死亡。只有对死亡有了更深入的了解，人才能更深刻地把握生命。死亡，其实就是一切事物的本质。”

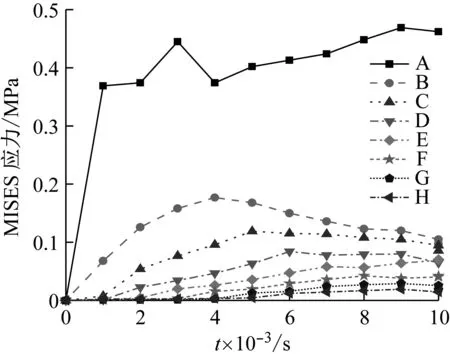
图3 代表单元的MISES应力-时程全曲线

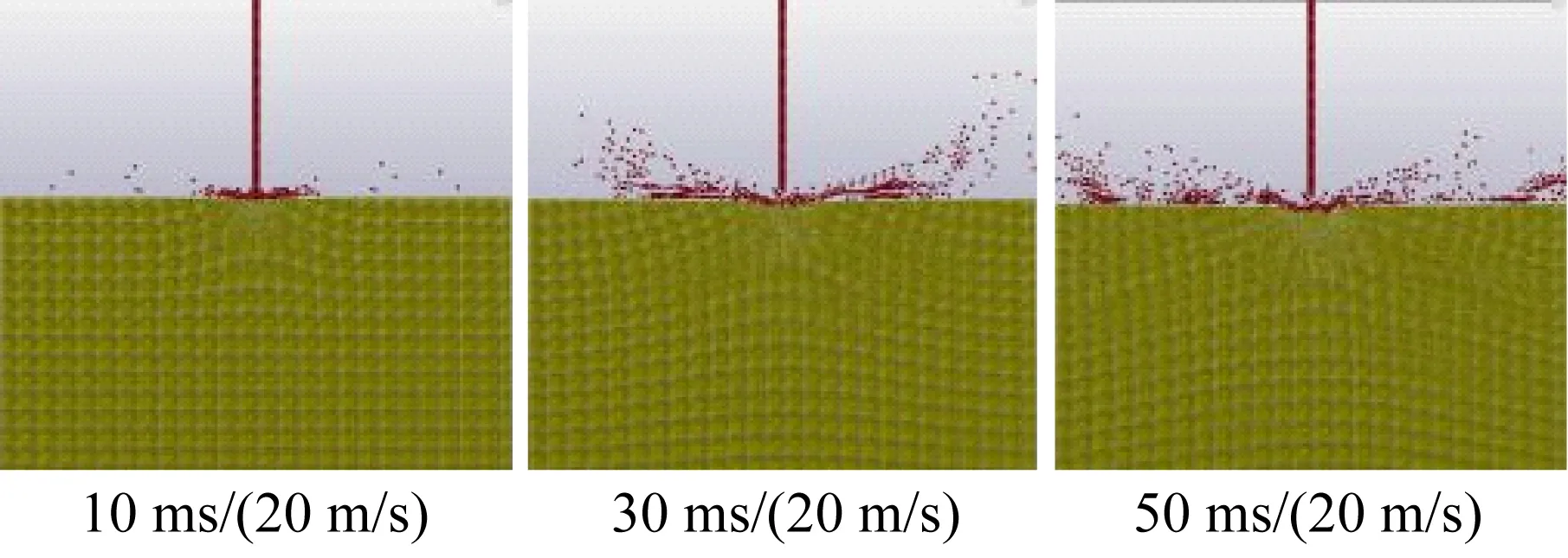
图4 冲埋成坑形貌对比图

图5为3种喷射压力条件下的冲埋深度-时程关系曲线对比图，可见冲埋速率随喷射压力的提升显著增大。比较0.04 s、0.08 s和0.12 s时刻对应的的冲埋深度值，可见冲埋深度随喷射压力的提升呈线性增长的趋势，如图6所示。

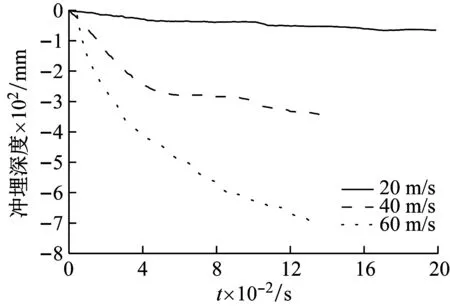
图5 冲埋深度-时程曲线

2.3.2 海床土体

结合实际设备情况，采用水射流速度为25 m/s、30 m/s和35 m/s进行计算分析，对应的喷嘴压力分别为0.3 MPa、0.45 MPa和0.6 MPa。

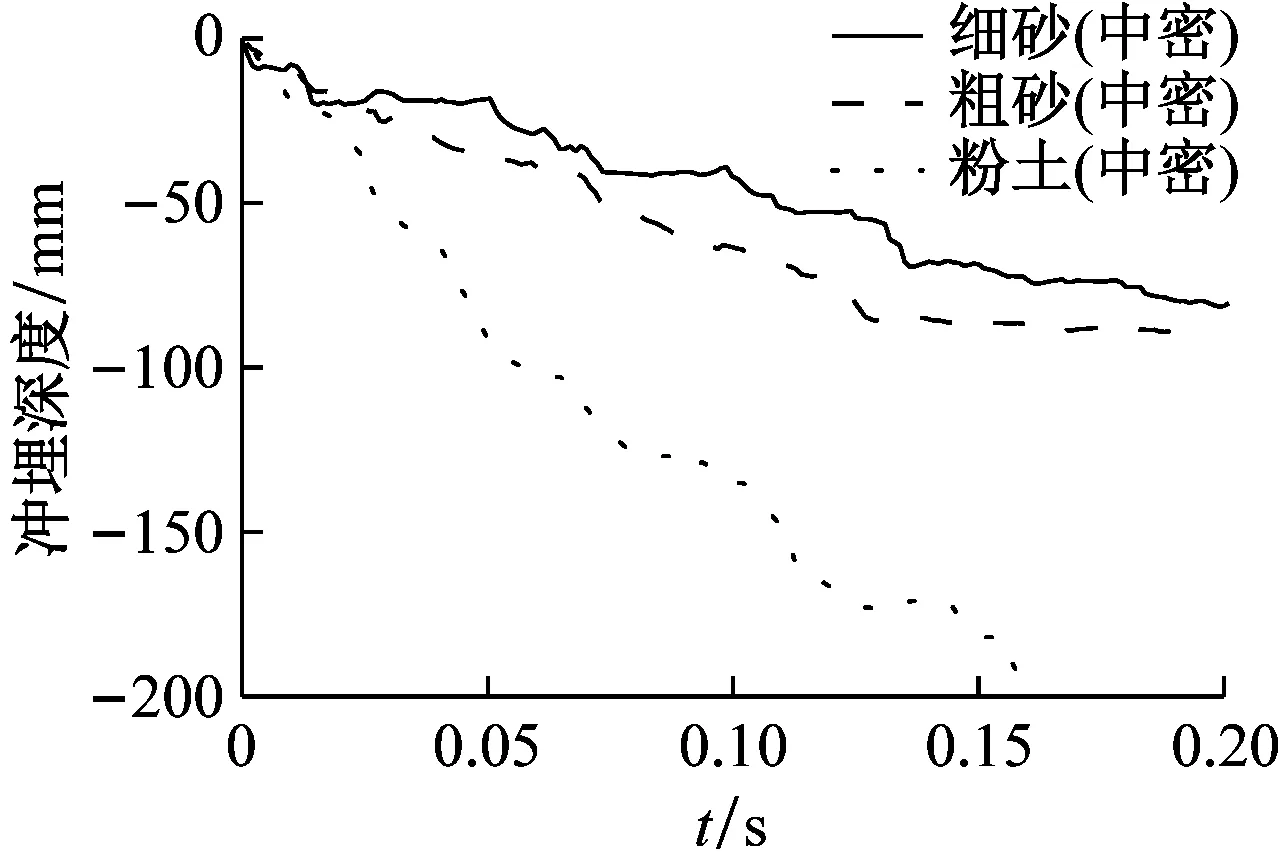
(1) 剪切模量

对中密细砂、中密粗砂与中密粉土3种具有相同密实度的海床土体进行冲埋仿真计算。3种海床土体的剪切模量分别为5.1 MPa、4.3 MPa和2.1 MPa。图7为3种水射流速度对应的3种海床土体冲埋深度-时程曲线对比图。由图7可知，冲埋速率随剪切模量的增大而减小，且水射流速度越大，剪切模量的影响越显著。此外，冲埋速率随冲埋深度的增加而急剧降低，分析原因是：①水射流侧向溅射受到边壁土体的阻碍而改变方向，使其对土体的剥离效果下降；②侧向土体边壁约束随冲埋深度的增加而加强，使得与水射流接触的土粒子的抗剪强度有一定的提升，从而提高了其抵抗水射流剥离的能力，导致冲埋速率显著下降。

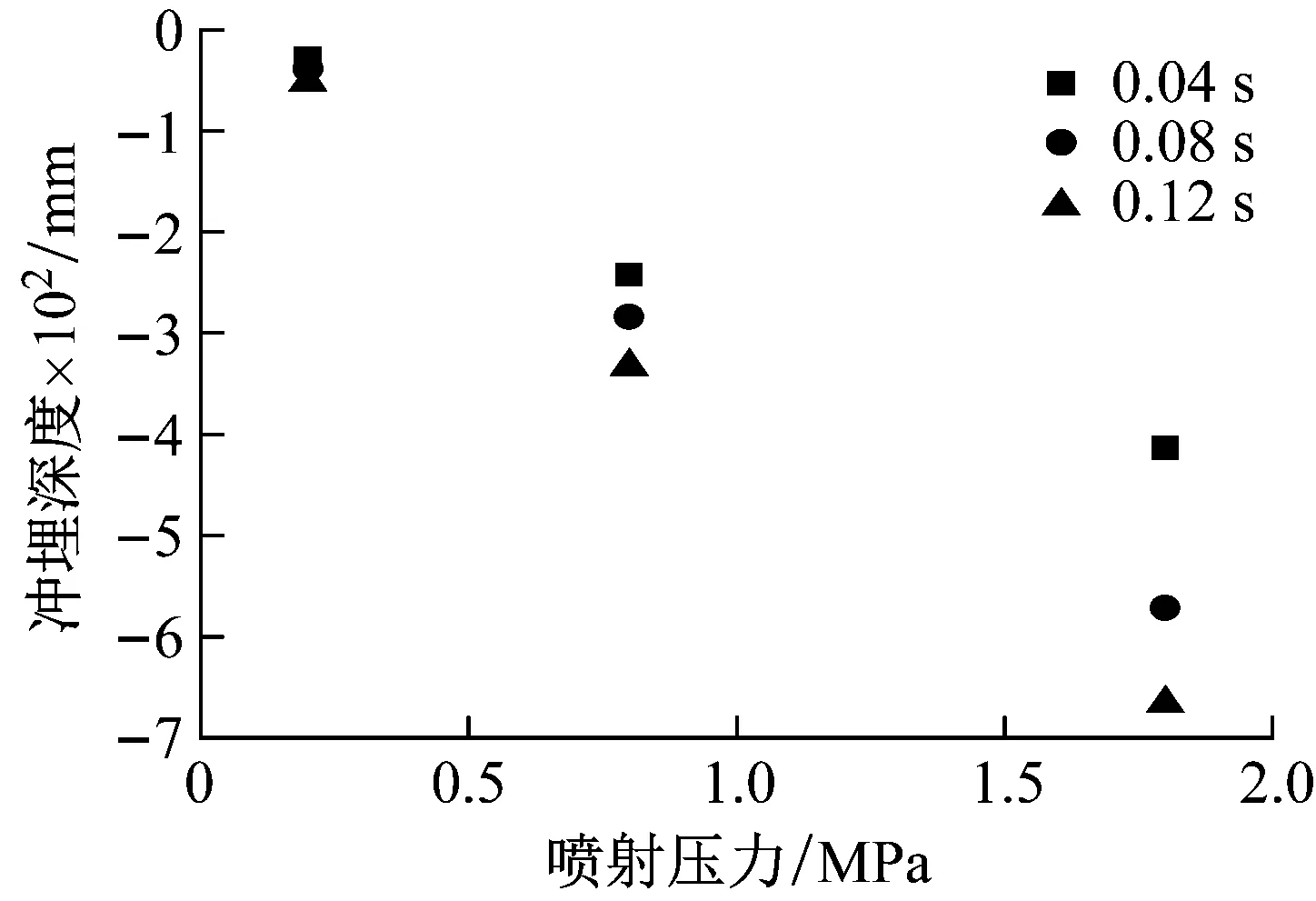
图6 0.04 s、0.08 s、0.12s时刻3种喷射压力下的冲埋深度

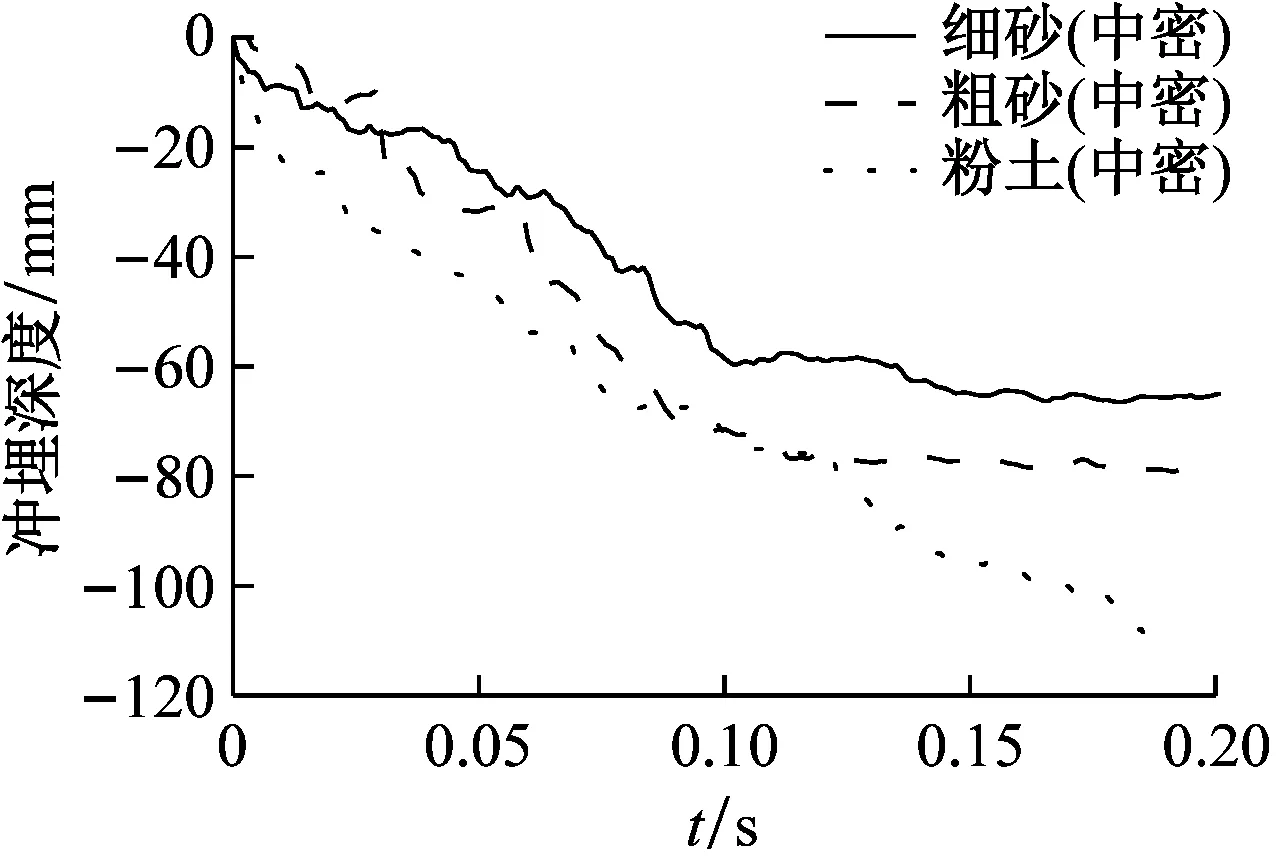
(a) 水射流速度为25 m/s

(b)水射流速度为30 m/s

(c)水射流速度为35 m/s

图7 3种水射流速度下相同密实度土体冲埋深度-时程曲线对比图

Fig.7 Comparison of scour depth-time curves of soils of the same compactness under three water jet velocity

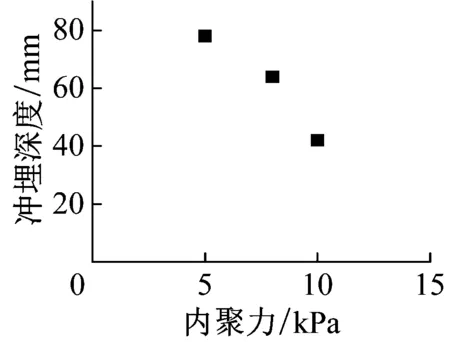
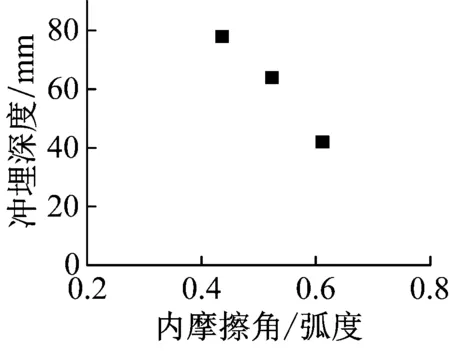
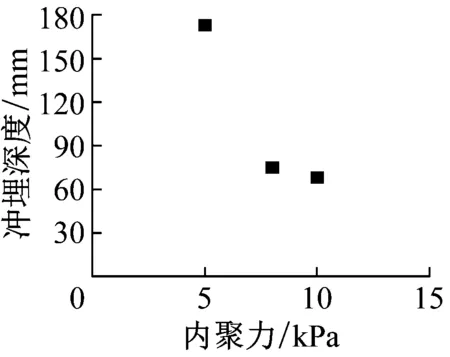
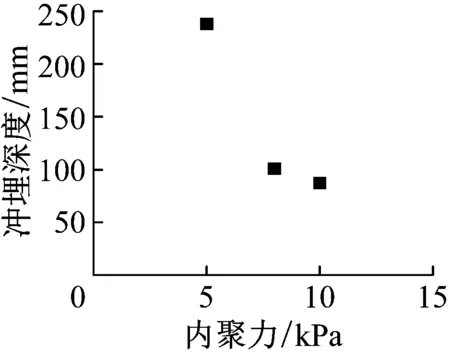
(2)内聚力与内摩擦角

(3)孔隙率

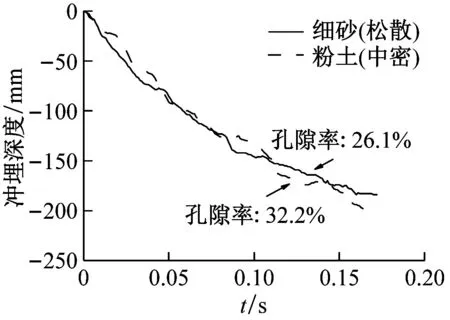
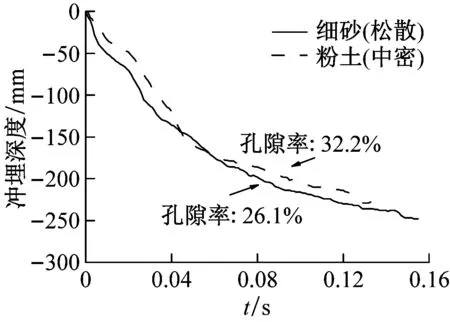
对比松散细砂与中密粉土两种海床土体条件下的冲埋深度-时程曲线，如图9所示。在水射流速度为25 m/s时，中密粉土海床土体的冲埋速率略大于松散细砂海床土体。但随着水射流速度的增加，冲埋速率渐趋一致，甚至在水射流速度为35 m/s时，中密粉土土体的冲埋速率略小于松散细砂。分析原因是：中密粉土海床土体孔隙水体积分数较高，使得其在水射流冲击下更容易坍塌；但孔隙水压力会随冲击荷载的增加而增大，在较大水射流速度条件下，中密粉土海床土体会由于内部孔隙水较多而产生更大的孔隙水压力，使得有效应力减小从而导致冲埋速率偏小。

虽然两种海床土体的孔隙率差别较大，但总体来说两条曲线大致一致，主要原因是中密粉土与松散细砂拥有完全相同的剪切模量。由此可见，相比剪切模量，孔隙率对冲埋速率的影响较小。

3 模型可靠度验证

模型参数均采用Bui等[12]中的数值，其中干土模型高20 cm，宽50 cm，密度为2.7 g/cm3，剪切模量为5.7 MPa，泊松比为0.3。水射流宽2 cm，速度为25 m/s。图10为参考文献[12]中的模型与本文模型模拟出的水射流侵蚀干土过程的形貌对比图，对应的时间分别为0.005 s、0.010 s、0.015 s及0.020 s。由图10可知，利用本文数值模型得到的水射流侵蚀土体成坑机制与文献报道保持一致。图11为水射流颗粒侵蚀深度-时程关系与文献中侵蚀深度-时程曲线的对比图。由图11可知，侵蚀深度-时程关系与文献结果一致，建立的数值模型准确可靠。

(a) 水射流速度为25 m/s

(b) 水射流速度为30 m/s

(c) 水射流速度为35 m/s

图8 土体内聚力及内摩擦角的影响

Fig.8 Effects of cohension and internal friction angel

(a)水射流速度为25 m/s

(b)水射流速度为30 m/s

(c)水射流速度为35 m/s

图9 孔隙率的影响

Fig.9 Effect of porosity

图10 与文献冲埋物理过程对比

4 曲线拟合

实际冲埋过程中，冲埋设备以某速度匀速向前运动，在保证冲埋深度的前提下，移动速度越快，冲埋效率越高。在水刀长度与设备移动速度确定的情况下，即单位土体被冲刷的时间确定的情况下，单位长度土体的冲埋深度与水射流喷射压力和海床土体条件有关。结合数值模拟结果，分别对3种喷射压力下(0.3 MPa、0.45 MPa和0.6 MPa)5种海床土体的冲埋深度-时程曲线进行拟合，选定曲线形式为y=axb(其中y为冲埋深度，x为冲埋时间，a和b为拟合参数值)，满足曲线过原点的条件。图12为3种水射流压力下5种海床土体的冲埋深度-时程曲线的模拟结果与拟合结果的对比图，可见拟合效果良好。表6为拟合公式参数的具体数值，可作为不同土体条件下选取合适的喷射压力的参考。

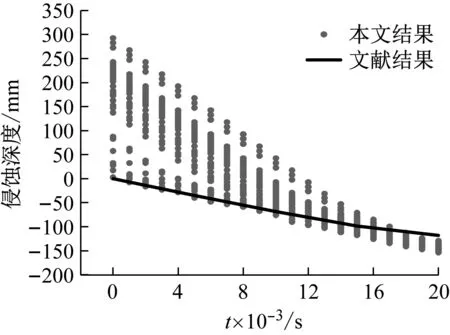
图11 与文献侵蚀深度对比

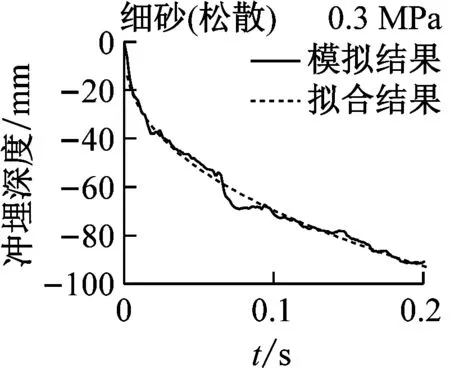
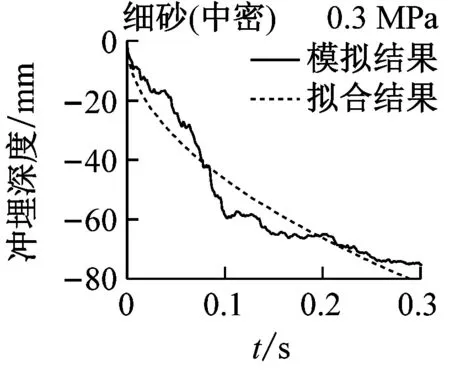
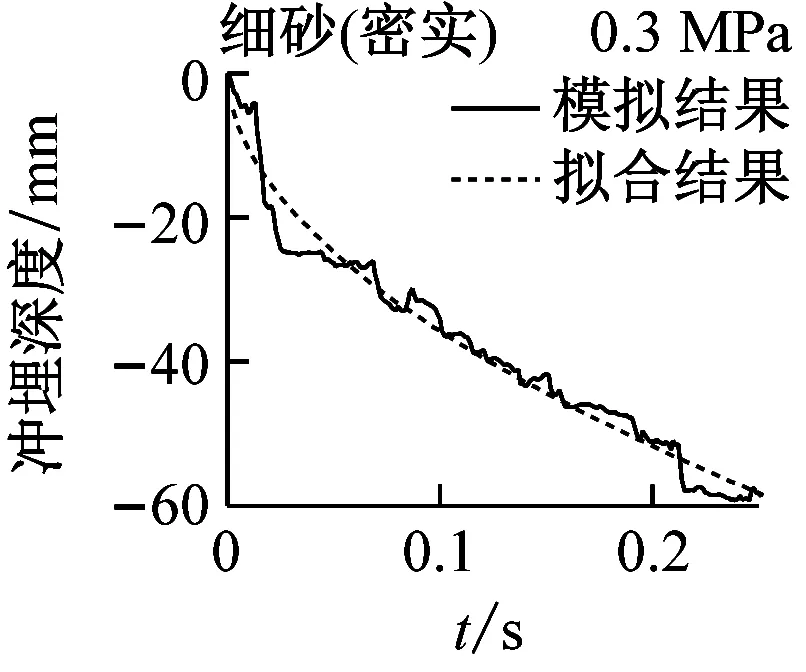
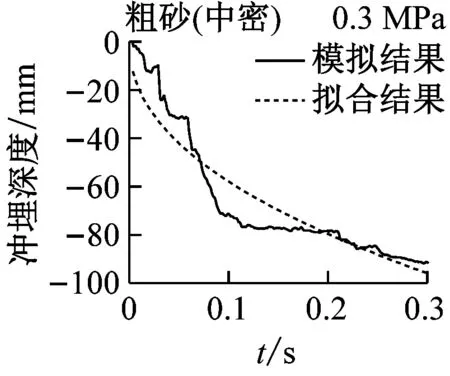
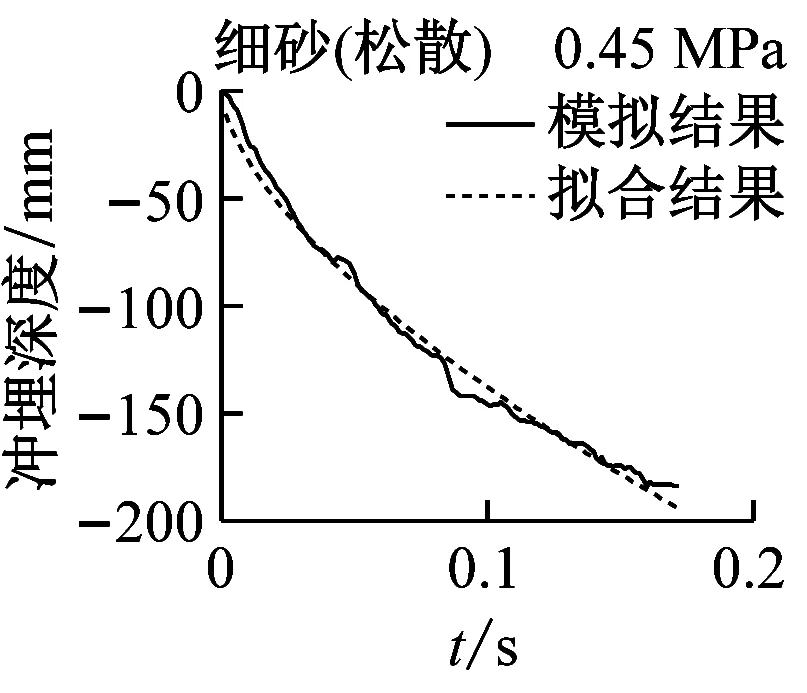
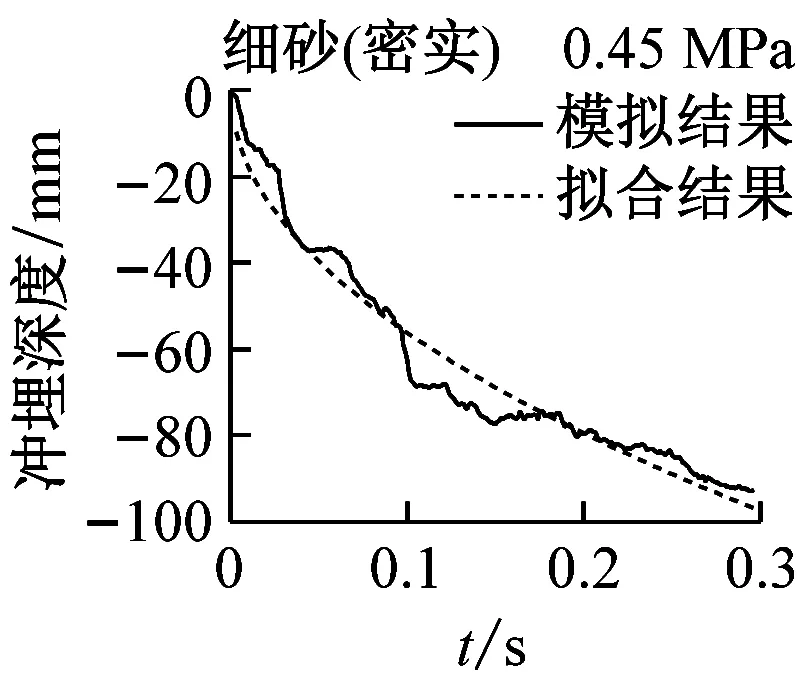
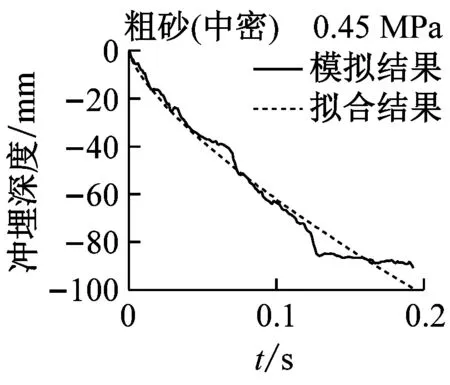
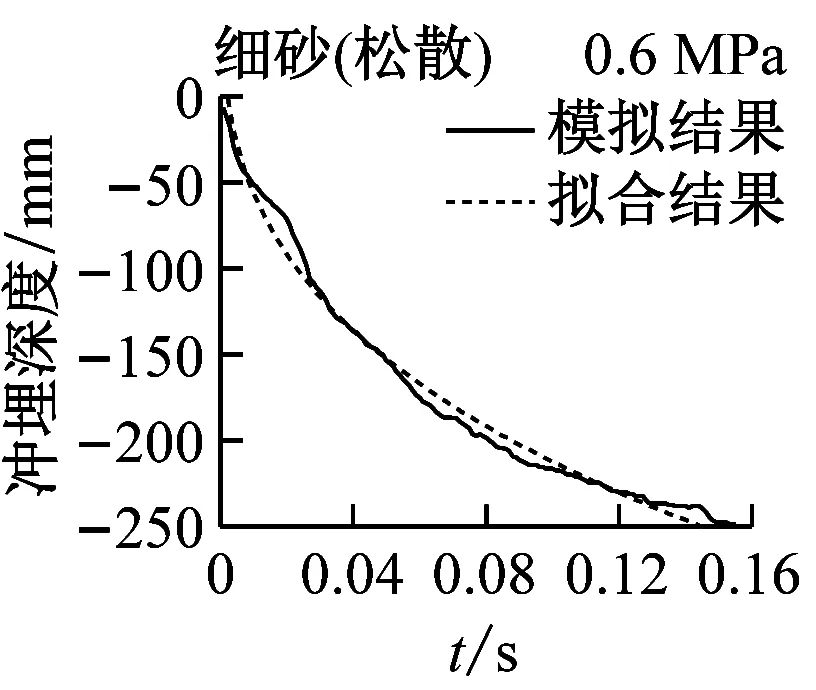
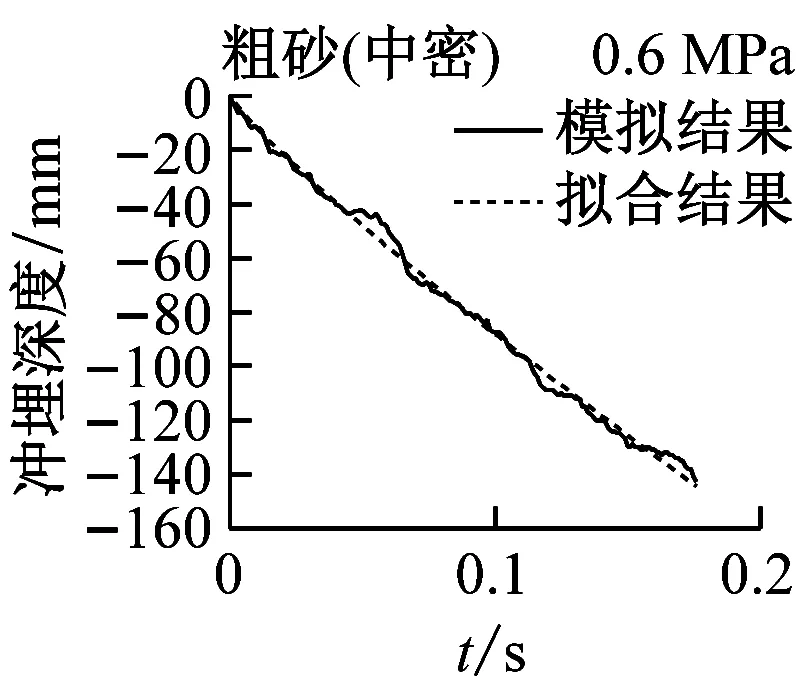
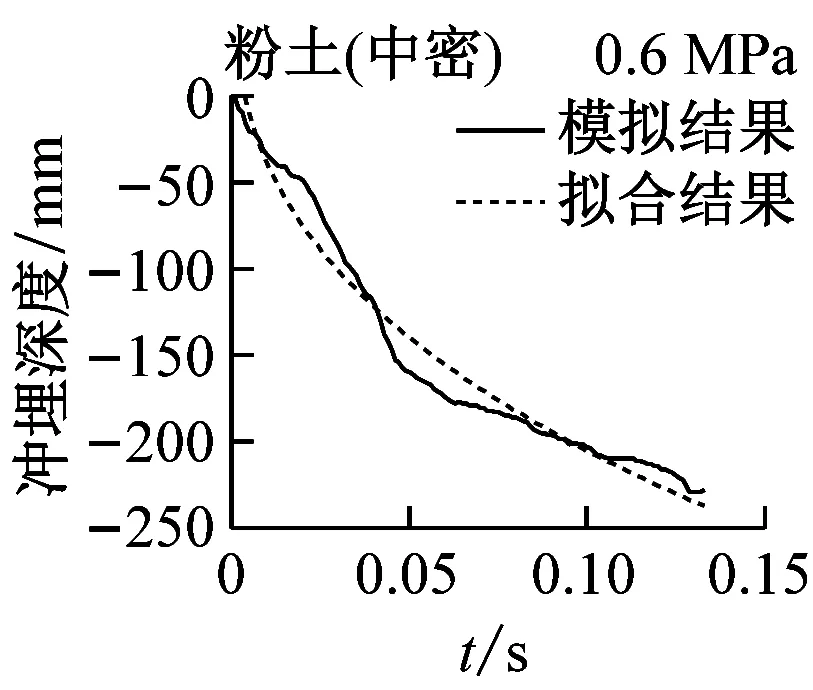
图12 模拟结果与拟合结果对比图

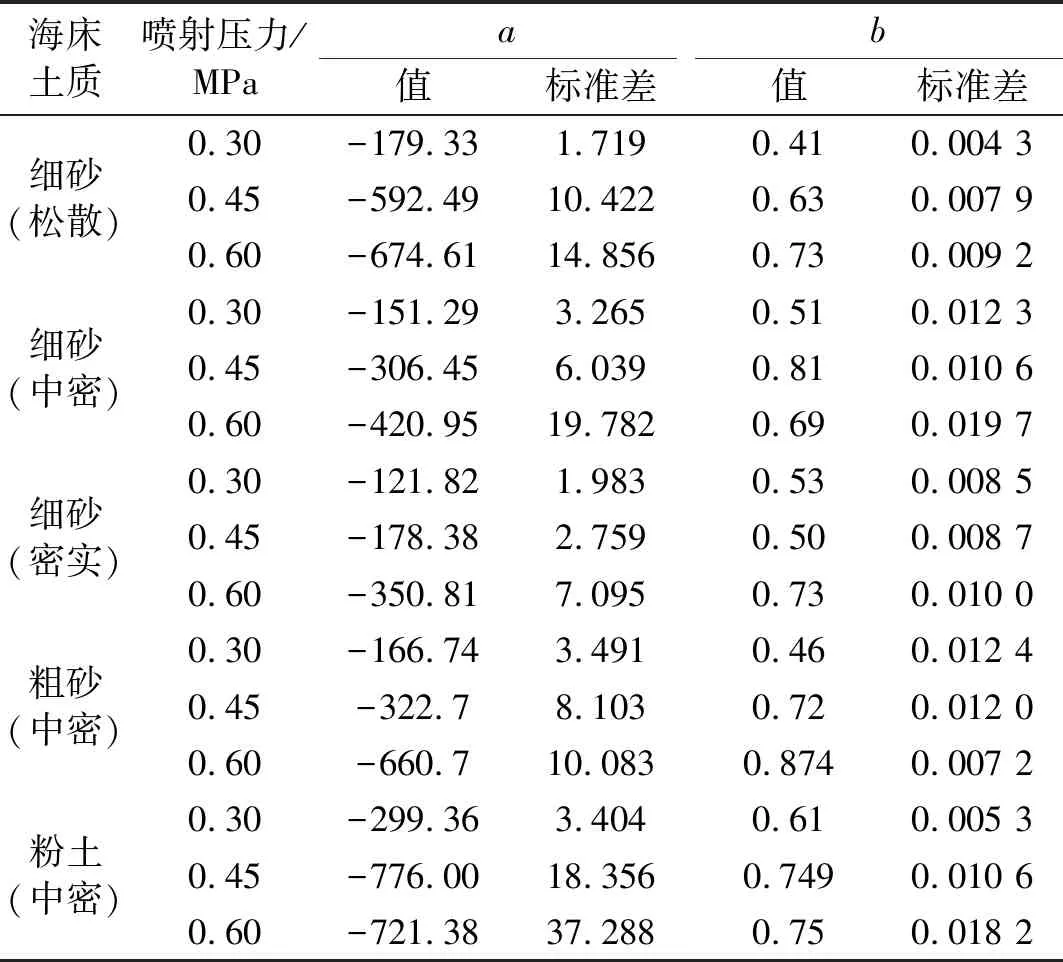
表6 拟合公式参数值

5 结 论

(1)应力波在海床土体内部沿水射流中心线方向形成，其能量随传播而耗散。应力最大值在水射流中心线与海床土体表面接触点处，从而使得冲击坑沿中心线形成。

(2)喷射压力对冲埋速率具有显著影响，喷射压力越大，冲埋速率越快。在较大喷射压力水射流的冲击下，海床土体演化为火山口的形状。同一时刻的冲埋深度随喷射压力的增大呈线性增长。

(3)对于具有相同密实度的砂质海床土体，剪切模量越大，相同冲埋条件下的冲埋速率越低。且水射流速度越大，剪切模量的影响越显著；对于细砂类砂质海床土体，相同冲埋条件下的冲埋速率随内聚力及内摩擦角的增加呈线性下降的趋势；土体孔隙率对冲埋速率的影响较小。

(4)通过与相关参考文献对比，证明了数值模型的准确性。通过拟合数值模拟结果，得到3种喷射压力下5种砂质海床土体的冲埋深度与时间的关系式，可作为不同海床土体条件下选择合适喷射压力的参考。