势函数特征参数调节随机共振及动车轴承故障检测研究

刘进军, 冷永刚, 张雨阳, 谭 丹, 范胜波

(1.天津大学 机械工程学院，天津 300350;2.天津城建大学 控制与机械工程学院，天津 300384)

近年来我国高速列车发展迅速，根据2016年新修订的《中长期铁路网规划》，到2025年全国高速铁路通车里程将达到3万公里。在高速铁路对促进社会经济发展、保障和改善民生等发挥重要作用的同时，高速列车运行的安全问题也越来越受到高度的关注。高速列车转向架的轴承是车组的关键部件之一，其运行工况较为恶劣，因此需要对其进行实时监测与故障检测诊断，以保障列车安全可靠的运行。目前针对列车滚动轴承故障的检测主要有轴温监测、油液分析、声学及振动信号检测分析等方法。随着信号采集设备以及信号处理方法的发展，振动信号采集分析法逐步成为故障检测与诊断的主要方法。

为了能有效提取与识别轴承等机械故障的特征信号，一些方法如小波变换[1-2]、经验模式分解EMD(Empirical Mode Decomposition)[3]、数学形态学[4]和非线性系统理论[5]等得到了广泛深入的研究与应用。其中非线性系统(如双稳系统、Duffing 振子系统等)中存在着非同寻常的随机共振现象而颇受关注。该现象因具有利用噪声增强微弱信号的新颖特点，而逐步成为机械故障诊断中的研究热点。为了能够将随机共振方法应用于诸如早期微弱故障信号的检测，人们克服了随机共振理论小参数条件以及低采样频比的限制，研究发展出了变尺度[6]、调制解调[7]、参数归一化[8-9]、多尺度噪声[10-11]、频域信息交换[12]等多种随机共振方法，这些方法在已工程应用中得到了一定的验证应用。

上述研究方法都涉及到非线性系统参数的调节，而系统参数的调节都会引起势函数特征——势垒高度和势阱间距的同时变化，这无疑给清晰观察势函数某一特征如何影响随机共振带来了困难。如果有一种方法能够单独反映势函数的势垒高度或势阱间距的变化，那么将有助于直观理解势函数特征对随机共振的影响，并可进一步将随机共振有效应用于实际中。文献[13]提出利用正弦函数构造势阱，通过调整波形的幅值和周期，实现势阱势垒高度和势阱间距单独调节。但是正弦势阱两侧的侧壁高度与势垒高度相同，从物理意义上理解，粒子可能会越出构造的势阱，落入两侧其他势阱中。因此该方法虽然能够将势垒高度和势阱间距分离，但非线性系统势函数类型被彻底改变，相应的系统随机共振特性也被改变，这并不利于实际应用。

为了能够单独观察理解系统势函数的势垒高度或势阱间距与系统随机共振的关系，在保证势函数类型不变的前提下，本文以非线性双稳系统为研究对象，提出基于势函数特征参数调节的随机共振方法。通过变量代换对势函数特征参数(Potential Function Characteristic Parameters,PFCPs)——势垒高度参数和势阱间距参数进行解耦，来掌握势垒高度和势阱间距的调节对势函数的影响。此外，为了解决低采样频率比随机共振难以实现问题，本文将势函数特征参数调节方法与频域信息交换方法(Frequency Information Exchange Method,FIE)相结合，给出频域信息交换和势函数特征参数调节的随机共振方法，并应用于高速列车滚动轴承故障的信号检测，以验证所提方法的可行性和有效性。

1 基于势函数特征参数调节的随机共振

1.1 势函数特征参数引入

经典随机共振理论中，随机共振现象的产生主要包括三大要素：非线性系统、满足小参数条件的信号及噪声。在三者的协同作用下，系统输出信噪比会在合适噪声强度下达到最大值，此类现象被称为随机共振现象。随机共振模型可由郎之万方程表示为

(1)

式中:A0和f0分别为周期驱动信号的幅值和频率；n(t)为噪声强度D的高斯白噪声，其均值和自相关函数满足：〈n(t)〉=0，〈n(t)n(t-τ)〉=2Dδ(τ)。U(x)为双稳势函数，通常表示为

式中:a和b为系统参数。势函数的势垒高度ΔU和势阱间距ΔL分别为

ΔU=a2/4b

(3)

(4)

由式(3)和式(4)可知，当调节系统参数a或b时，都会导致势函数U(x)的势垒高度和势阱间距同时发生变化，对势函数的变化规律不易掌握。为了能将势垒高度或势阱间距分离，引入势函数特征参数，即引入势垒高度参数h和势阱间距参数w来重新描述势函数的特征。由参数h和w构建的双稳势函数变为

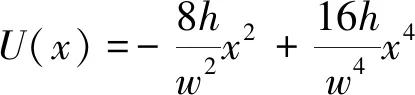
(5)

式中:h0，w0;系统参数与势函数特征参数对应关系为a=16h/w2及b=64h/w4。根据式(3)和式(4)可得由参数h和w描述的势垒高度ΔU和势阱间距ΔL为

(6)

(7)

根据式(6)和式(7)可知，通过变量代换后，势函数特征参数h和w为相互独立互不耦合的，因此实现了势垒高度和势阱间距的解耦，可以分别独立考察势垒高度或势阱间距对系统势函数的影响。而现有的系统参数调节法则无法直接得到势函数的变化规律，它属于一种非解耦的系统参数调节方式。为了更好地说明这一点，图1是不同参数h和w下的势函数曲线。假设参数h=0.3和w=2得到势函数曲线(实线)是基准曲线，那么当w=3增大势阱间距时，将得到比基准曲线势阱间距大而势垒高度保持不变的势函数曲线(短划线)；当h=0.6增大势垒高度时，将得到比基准曲线势垒高而势阱间距保持不变的势函数曲线(圆点线)。因此，通过调节势函数特征参数h或w可方便实现势垒高度或势阱间距的单独调节。

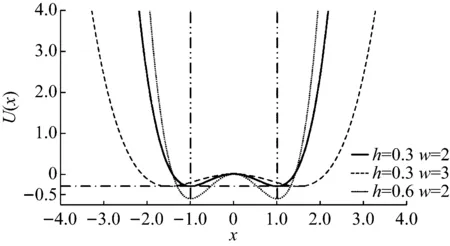
图1 不同势函数特征参数的势函数曲线

1.2 势函数特征参数对随机共振的影响分析

根据郎之万方程所描述的单个布朗粒子的运动行为可知，式(1)可认为是描述布朗粒子B在双阱势场U(x)中的运动模型，如图2所示。图2中的布朗粒子B，在给定的周期力和随机力联合驱动下，能否越过势垒“P”点，取决势垒高度h的大小。如果h过大，布朗粒子不会越过“P”点落入另一势阱中，即出现“欠共振”状态。减小势垒高度h，布朗粒子则可能在两势阱间往复跃迁，即出现“双稳随机共振”状态。但如果h持续减小并趋于零，势函数也就趋于零，则式(1)会趋于一阶积分系统，系统不再属于双稳随机共振系统。为了能够保证系统达到平稳规律的双稳跃迁状态，需要选择合适的势垒高度h。

而势阱间距w则对应于布朗粒子运动的行程，关系到双稳系统的输出值。在其跃迁状态下，w越大，系统输出值也就越大。但如果持续增大w，可能会破坏粒子的双稳跃迁状态，因为运动行程越大，粒子运动出某个势阱所需的时间越长，其单势阱驻留时间也就越长。根据经典随机共振理论[14]，系统产生双稳随机共振时的时间尺度匹配条件为：布朗粒子在单势阱中的平均驻留时间要和周期驱动力的半周期时间相当。所以当过长的势阱驻留时间与周期力的半周期时间不相当时，已有的双稳跃迁状态也就会被破坏。

根据势垒高度h和势阱间距w与双稳随机共振的关联特点，下节将讨论以势垒高度为主要调节和以势阱间距为辅助调节的最优势垒寻优方法，以方便控制双稳随机共振的实现。

图2 双稳势阱中的布朗粒子运动

1.3 基于势函数特征参数调节的随机共振及其信号检测机制

根据上节势函数特征参数的引入，随机共振模型式(1)可改写为

(8)

根据随机共振理论，在噪声、周期驱动信号和系统三者协同作用下，布朗粒子越过势垒在双势阱间往复跃迁的现象被称为随机共振现象。其发生的条件：① 在得到部分噪声能量的补给后，周期驱动信号的幅值要大于系统跃迁临界值；② 布朗粒子往复跃迁时，其在某势阱中的平均驻留时间TK(TK=1/rK，rK为Kramers逃逸速率)要与周期驱动信号周期的一半T0/2相等，即二者达到统计同步匹配的状态。依照此条件，下面给出势函数特征参数调节的随机共振信号检测方法。

首先，噪声驱动的布朗粒子在势阱间的跃迁速率(Kramers逃逸速率)与势函数参数的关系可表示为

(9)

假设某待检测信号的特征频率为ft，则根据时间尺度同步匹配条件有

(10)

因频率ft已知，噪声强度D可通过对输入信号进行估计得到，则势垒高度h与势阱间距w之间的关系可由式(10)确定，当h给定时w也就可以相应得到，反之亦然。二者可构成势函数参数对(h,w)。将每组参数对代入随机共振模型式(8)中，以四阶Runge-Kutta法数值求解可得到系统输出结果。因此，该方法可通过势垒高度h一个参数的调节，实现对信号的检测。而传统的参数调节法则需要同时对系统参数a和b进行非解耦的调节，其计算相对复杂。

其次，以系统输出信噪比作为系统是否进入双稳随机共振状态的判定指标。系统输出信噪比定义为

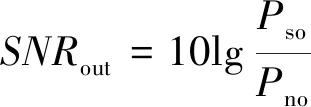
(11)

式中:Pso为输出信号的功率;Pno为输出噪声的功率。根据每组势函数参数对(h,w)由式(11)可求得相应的系统输出信噪比，选取最大输出信噪比对应的参数对作为系统的势函数特征参数，代入式(8)中并进行数值求解得到系统的随机共振输出。

需要说明的是，势垒高度调节的搜索步长Δh以及搜索范围设置要考虑采样频率的大小。因为数值计算的步长通常取为1/fs，在数值计算过程中，原始信号的幅值会按照1/fs削弱。而合适的势垒高度的数量级与削弱后的信号幅值相当，才可能保证系统、信号及噪声协调匹配的随机共振输出。因此采样频率越大时最优的势垒高度也越小。因本文研究的目标信号为微弱信号(幅值小于1)，故势垒高度h的搜索范围可设定为(0,1/fs)，而势垒高度的搜索步长Δh越小，则可以得到最优势垒高度值越精确。

下面以含噪信号检测为例给出说明。令输入信号中的高斯白噪声强度为0.2，周期信号的幅值为0.05，信号频率为0.05 Hz。采样频率为5 Hz，数据点数为1 000。原始信号的时域和频域波形,如图3所示。由于背景噪声的存在，输入信号的信噪比(-25.26 dB)较低，因此从频域图中无法清晰识别出该周期信号。

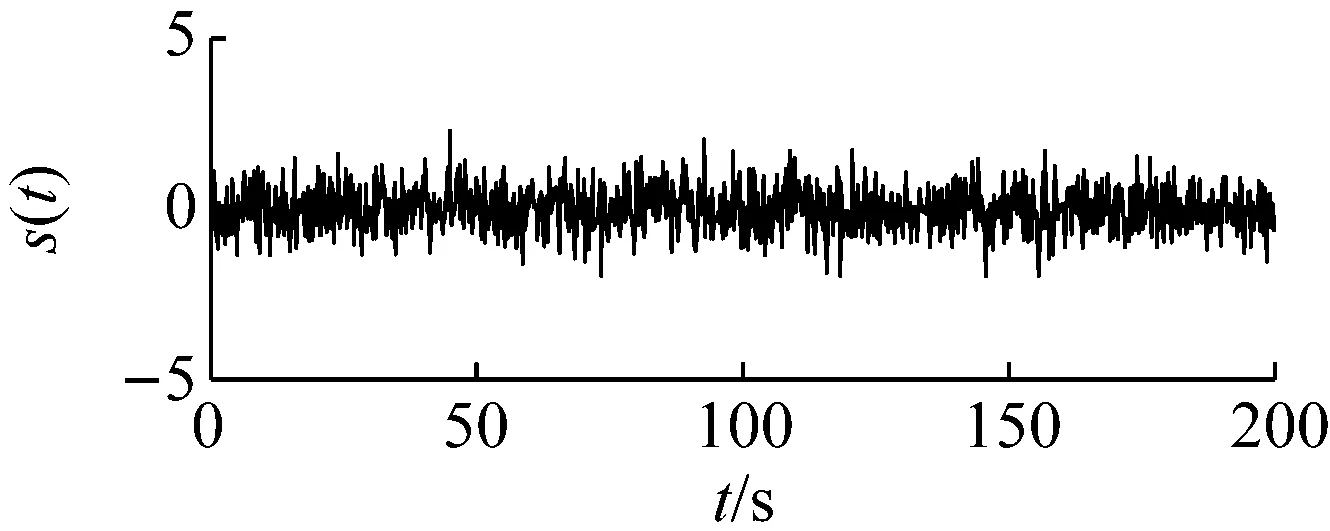
(a)

(b)

设定势垒高度h的搜索范围在(0,0.2)区间，搜索步长Δh=0.001，于是得到最大输出信噪比(-9.87 dB)对应的最优势函数特征参数为h=0.015和w=0.708。将此参数对(0.015, 0.708)代入式(8)计算得到系统输出响应的时频图,如图4所示。从图4可知,0.05 Hz周期信号的特征谱线。

(a)

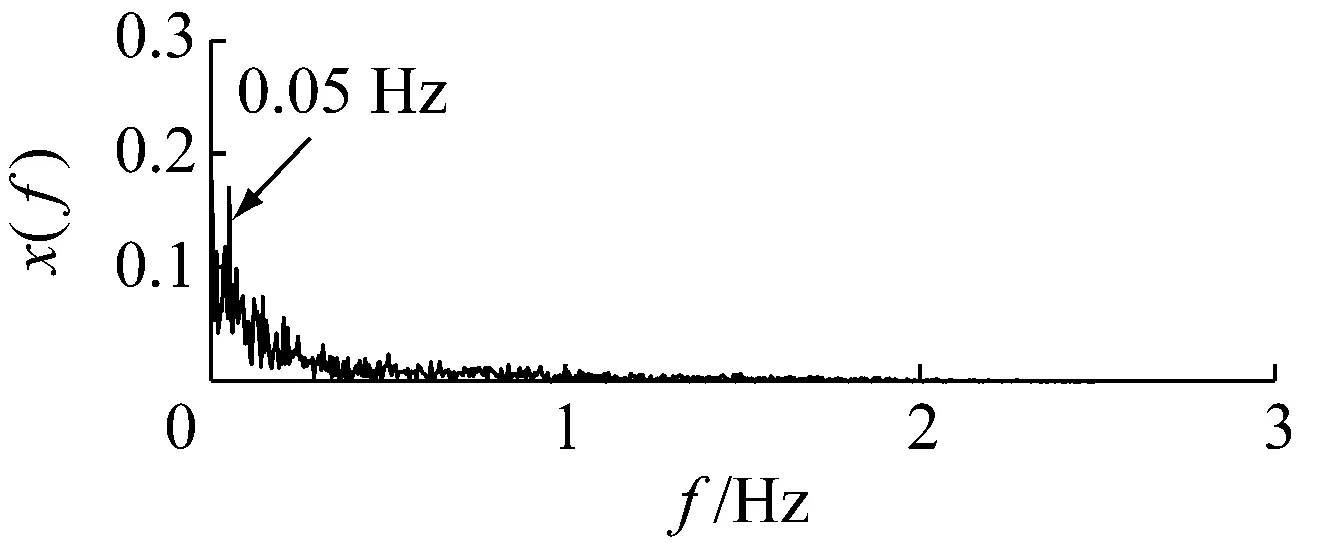
(b)

2 低采样频比的频域信息交换技术

对于采样频率与特征信号频率之比小于50的低采样频比信号，其双稳响应通常很难达到随机共振状态。为解决此问题，本文引入FIE来实现低采样频比的随机共振。所谓频域信息交换，实际上就是将处在高频段的特征信号通过单边带调制方法与低频段信息交换，以满足随机共振对采样频比的要求。由于文献[12]在频域信息交换时首先采用快速傅里叶变换得到频域信息，因此不可避免地会存在频谱泄露的问题。为了克服这一问题，本文探讨了基于滤波器技术的时域换频方法，其原理流程如图5所示。由图5可知,基准低频信息sl(t)是指采样频率fs与信号频率之比大于50的频段处信息。令基准低频为fl，且令基准低频信息sl(t)的频域范围为(0,B)，则fl∈(0,B)且fs/B50。相应的目标信号st(t)的频带为(ft-fl,ft-fl+B)，ft为目标信号的特征频率，则单边调制时的载波频率为ft-fl。为避免信号处理过程出现频带重叠，文中所采用低通滤波器的通带必须和高通滤波器的阻带相同，取为(0,B)；带通滤波器的通带也要和带阻滤波器的阻带相同，取为(ft-fl,ft-fl+B)。因此，低通、带通滤波器的通带带宽与高通、带阻滤波器的阻带带宽相同，均为B。

需要说明的是，之所以采用高通、带阻滤波器滤除基准低频和目标信号频率处的信息来获取剩余信号信息，是因为在用低通、带通滤波器提取基准低频和目标信号的信息时，信号的相位会发生变化，因此不能将原信号直接减去提取的基准低频和目标信号信息来获取剩余信号信息。此外，为了能够有效提取特征频率处的信息，本文采用椭圆滤波器对目标信号进行滤波，因为椭圆滤波器比巴特沃斯、切比雪夫等滤波器具有更窄的过渡带。

图5 频域信息交换流程图

假设低通、高通、带通和带阻滤波器分别用LPF、HPF、BPF和BSF表示。通过用LPF、BPF可以分别提取出基准低频信息sl(t)以及目标信号信息st(t)，通过HPF和BSF滤波器得到基准信息和目标信息滤除后的信息sf(t)，即有

(12)

(13)

(14)

由式(14)可知，因频域信息交换处理数据s′(t)中的特征信号频率与采样频率之间的频率间距增大，其采样频比超过了50，因此为实现双稳随机共振达到检测特征信号的目的而创造了条件。

3 基于势函数特征参数调节和频域信息交换的随机共振信号检测

将势函数参数调节方法与频域信息交换技术相结合，既可以直观理解势垒或势阱变化对随机共振的影响，又能够克服采样频比对随机共振的限制，因此频域信息交换与势函数参数调节的结合将有助于信号随机共振的检测实现。这一信号检测方式的流程图，如图6所示。其执行过程是：首先将原始数据进行频域交换，将高频段的目标特征信号交换到基准低频处，得到换频后的数据s′(t);然后将数据s′(t)输入到势函数特征参数调节的随机共振系统中进行处理，其相应的随机共振模型由式(8)变为

(15)

图6 基于势函数特征参数调节SR和频域信息 交换的信号检测流程图

按照“1.2”节势函数特征参数的调节方法，找出最大输出信噪比对应的特征参数对，并代入式(15)中，数值得到系统的随机共振响应，检测出基准低频处的目标信号。最后将检测出的信号进行频域信息恢复，得到实际目标信号的检测结果。

以含噪信号检测为例进行说明。令周期信号的幅值和频率分别为0.05和125 Hz，噪声强度为0.2。数据采集长度为4 000，采样频率为1 000 Hz。原始输入信号如图7所示。显然背景噪声中的原始输入信号不可识别。如果直接采用势函数特征参数调节的随机共振方法对输入信号进行处理，得到最优势函数参数的系统响应如图8所示。从图8的频谱中无法确认125 Hz特征信号的存在，这是由于信号的采样频比1 000/125=8小于50造成的。下面采用频域信息交换(换频)和势函数特征参数调节的随机共振方法处理。

(a)

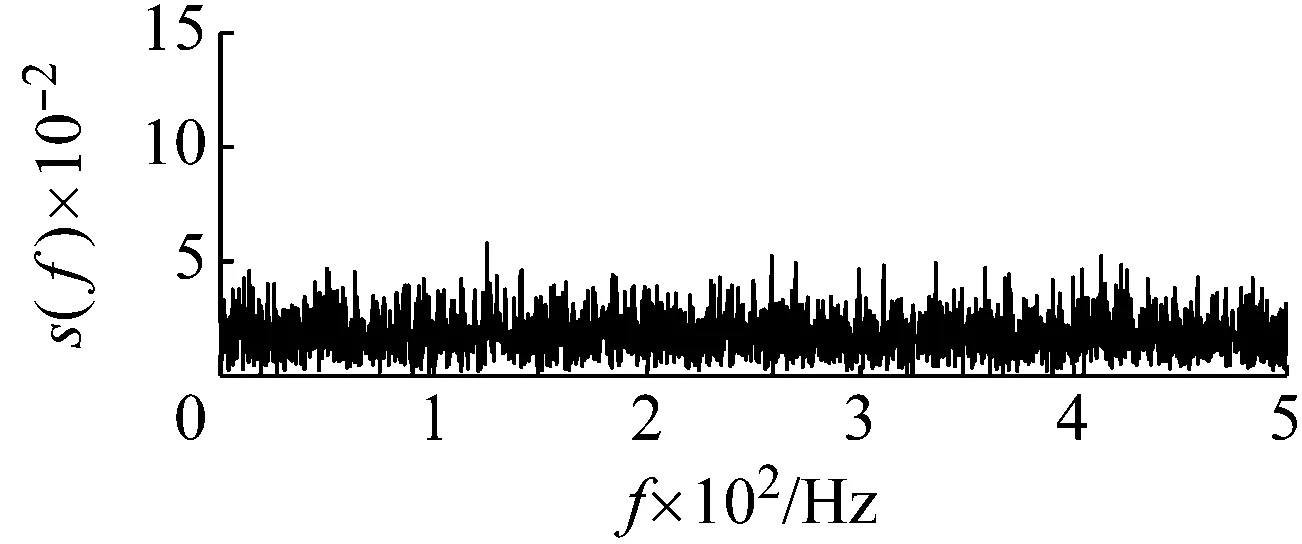
(b)

(a)

(b)

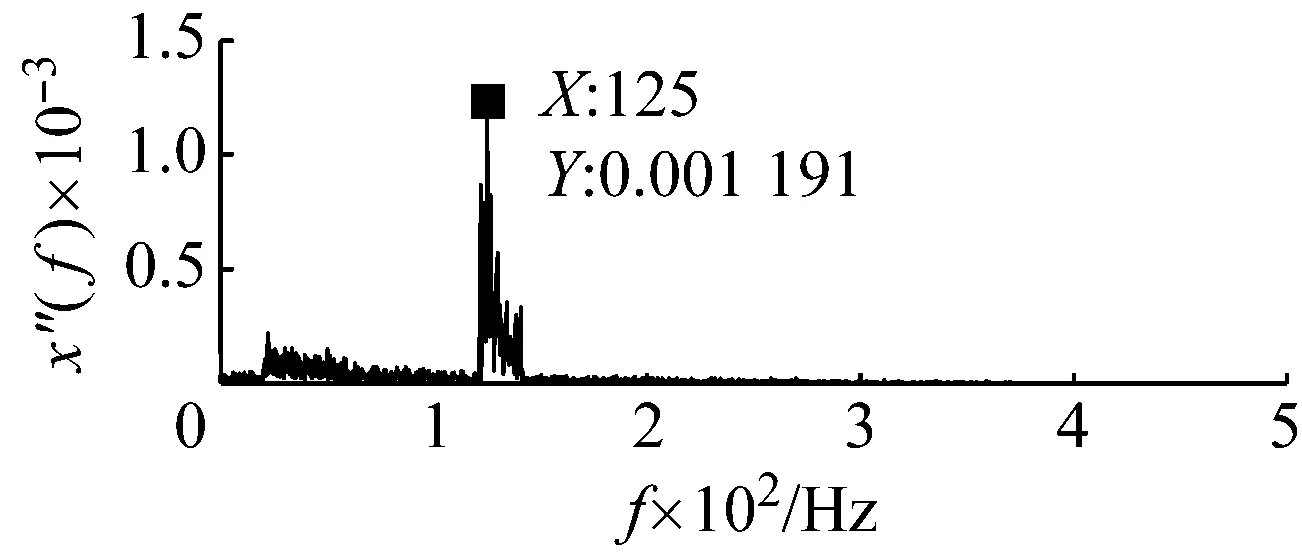
首先令基准低频为4 Hz，基准低频信息的频带为(0,20 Hz)，则目标信号所在的频带应为(121 Hz,141 Hz)，调制载频为121 Hz。频域信息交换后，对数据进行随机共振处理得到最优势函数特征参数(h=0.000 06,w=0.005 3)的系统输出如图9所示。从图9(b)可知，在基准低频4 Hz处有明显的谱线。通过频域信息逆交换恢复后，可确认125 Hz目标信号的存在，如图10所示。

4 动车转向架轴承故障诊断

4.1 转向架轴承模拟实验台

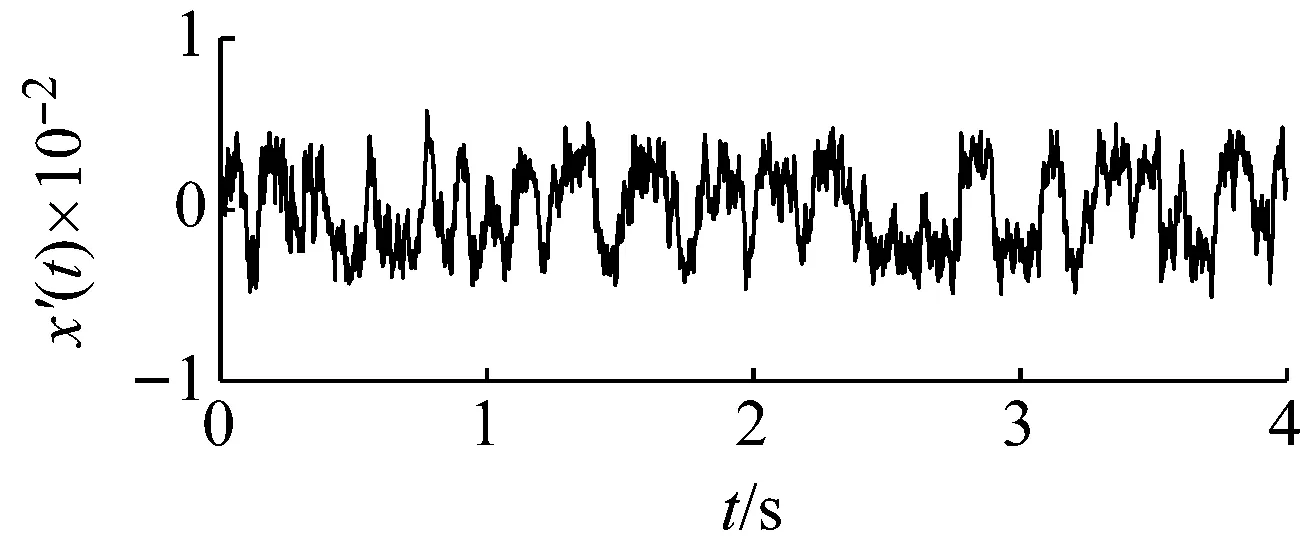
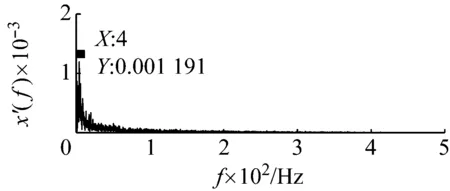
由于材料缺陷，加工或者装配不当，润滑不良，水分或者异物侵入等原因都可能导致转向架轴承的损坏。即使在装配和使用维护都正常的情况下，经过长时间、高速、负载运行后，轴承也会出现疲劳剥落和磨损等现象，影响列车的正常工作。本文以CRH380BL动车组所采用的转向架轴箱轴承的内、外圈及滚动体点蚀剥落故障为研究对象进行分析。该转向架轴箱轴承由舍弗勒公司提供，图11是轴承故障测试实验台。为了模拟满载(17 t)工况下轴承的运行状态，本实验台利用螺栓框架结构压缩三根弹簧，弹簧的弹力再通过半圆端盖与轴承外圈的接触，对轴承施加载荷，如图11负载部分所示。CRH380BL动车组设计最高时速可达380 km，试验中测试时速为260 km，对应的转子转速为1 590 r/min，即转频 等于26.5 Hz。将加速度传感器布置在半圆端盖上测试轴承的振动信号，使用NI PXI-1033信号采集仪对轴承振动信号进行采集，采样频率设为5 000 Hz，采样时间为2 s。表1给出了轴承的主要参数。

(a)

(b)

(a)

(b)

表1 滚动轴承主要参数

图11 转向架轴承测试实验平台

4.2 轴承故障分析

4.2.1 外圈故障分析

以轴承外圈轻度点蚀剥落故障为例，对外圈内表面加工故障。轻度故障对应的平均加工深度为：0.18～0.27 mm。

轴承外圈的故障特征频率可由下式给出

(16)

式中,fi为转子转频26.5 Hz，其他参数可参考表1，经计算可得到外圈对应故障频率理论值为193.8 Hz。

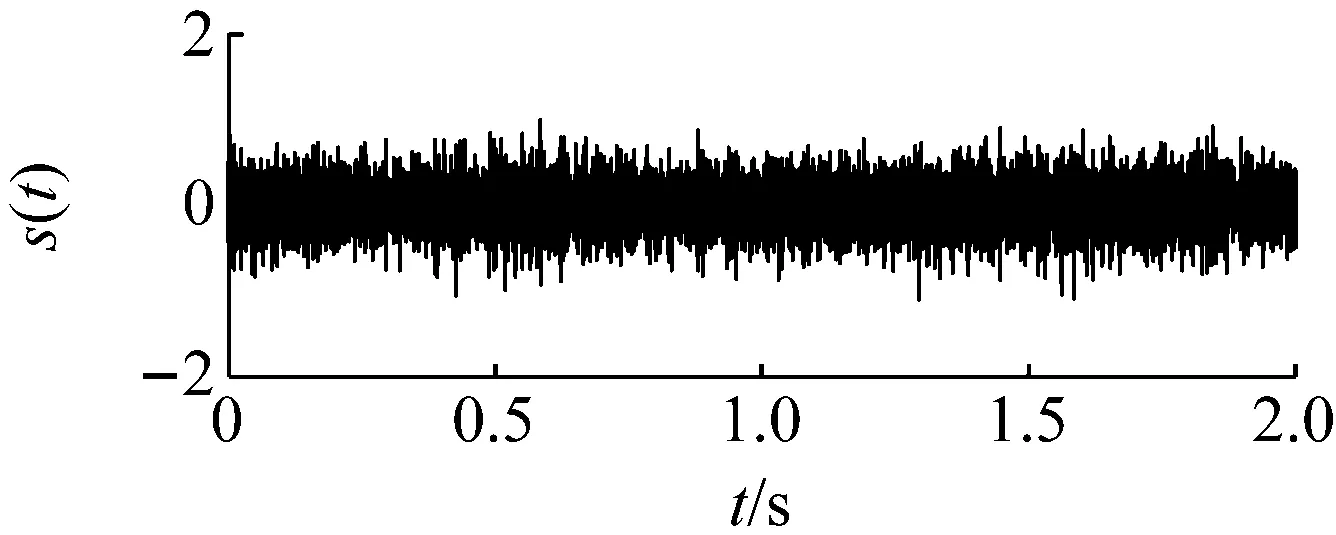
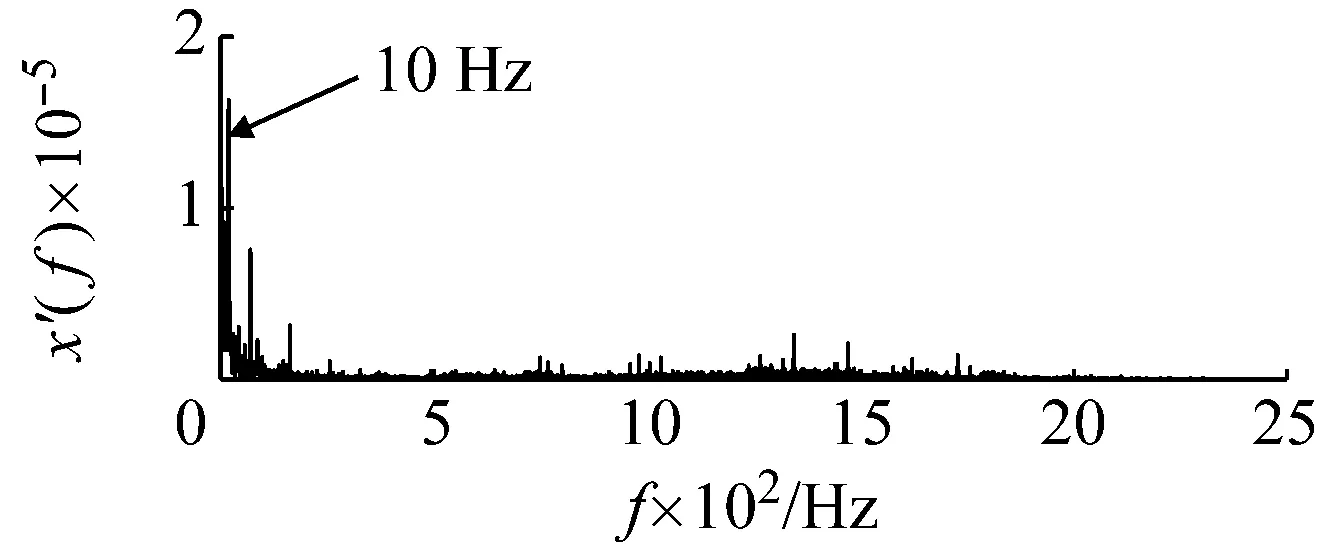
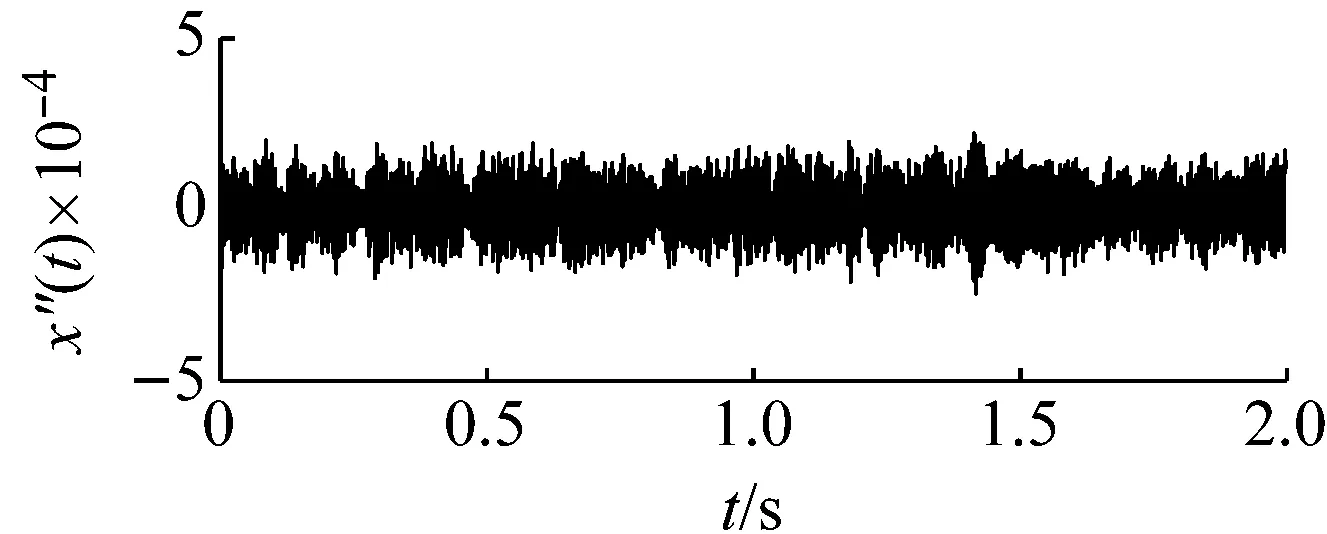
图12为外圈故障的原始采集信号，由于较强的高频成份及背景噪声的存在，故障信号比较微弱，而无法判定故障的存在。采用本文提出的基于频域信息交换和势函数特征参数调节的随机共振信号检测方法对其进行处理。首先根据频域信息交换思想，基准低频频率选为10 Hz，低频频带为(0,100 Hz)，则目标信号的所在频带为(183.8 Hz,283.8 Hz)，相应的载频为183.8 Hz。然后噪声强度值估算约为0.07。由于采样频率和信号频率较大，势垒调节步长相应设置为1×10-7，得到最优势垒高度和势阱间距参数对为(4×10-7，1.9×10-4)。将势函数特征参数对代入随机共振模型式(15)，得到系统响应如图13所示。在基准低频10 Hz处可以看出明显的谱峰。将频域信息恢复，谱峰相应出现在194 Hz处，如图14所示。即可判定外圈故障的存在。

(a)

(b)

(a)

(b)

(a)

(b)

4.2.2 内圈故障分析

以内圈表面中度剥落故障为例进行分析。中度剥落故障的平均剥落深度为0.6 mm，剥落沿内圈轴线方向。同样轴承内圈的故障特征频率可由下式给出

(17)

式(17)的参数与式(16)参数相同，可算出内圈对应故障频率的理论值为256.7 Hz。

当轴承存在内圈故障时，内圈周期性回转运动会激起支撑轴承系统的振动，如81.5 Hz、163.5 Hz以及245.5 Hz处存在明显的谱线，此外还会激起轴承系统的高频固有振动。因此，内圈故障特征频率会受到复杂的调制而不能从频谱中识别出来，如图15所示。

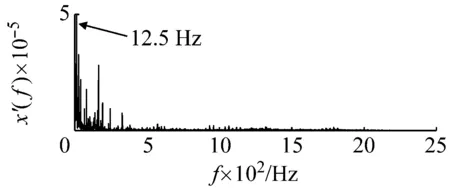
采用本文提出的方法对其进行处理。基准低频频率以及低频频带选择与外圈故障采用的频率和频带相同。因此内圈故障特征信号所在频带为(246.7 Hz,346.7 Hz)，相应的载频为246.7 Hz。原始采集信号噪声强度估算约为0.012 7。同样由于采样频率和信号频率较大，势垒调节步长相应设置为1×10-7，得到最优势垒高度和势阱间距参数对为(3×10-7，2.4×10-4)。将PFCPs对代入SR模型式(15)，系统响应如图16所示。在频率12.5 Hz处可以看出明显的谱峰。根据频域信息恢复后的频谱图17，可发现在259 Hz处出现了明显的谱峰，与理论计算值256.7 Hz非常接近，因此可判定内圈故障的存在。

(a)

(b)

(a)

(b)

(a)

(b)

4.2.3 滚动体故障分析

以滚动体表面中度剥落故障为例进行分析。滚动体中度平均剥落深度为0.4 mm。轴承滚动体的故障特征频率可由下式给出

(18)

式(18)的参数与前两节采用的参数相同，可算出滚动体对应故障频率的理论值为92.6 Hz。

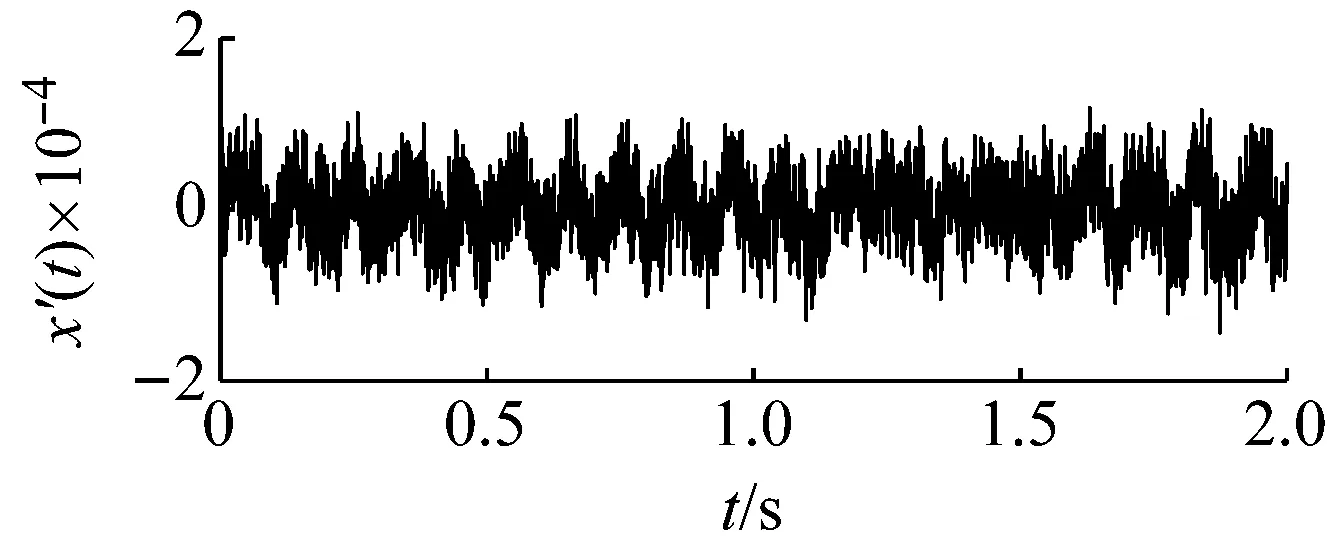
图18为采集的滚动体原始信号，可以看出由于系统存在丰富较强的高频成份，包含滚动体故障特征频率的低频成份受到了较大压制而无法识别。同时在滚动轴承运行时，除了滚动体自身的旋转外还伴随有保持架的转动。因此当滚动体存在故障时，其故障频率会受到保持架旋转频率的调制。根据保持架旋转频率公式fc=1/2(1-d/Dcosβ)fi和前文给定参数，可以计算出保持架的旋转频率约为11 Hz。因此调制后的滚动体故障频率可能为103.6 Hz，其二倍频成份可能调制到196 Hz附近。以103.6 Hz为目标信号进行检测，基准低频频率同样设定为10 Hz，低频频带为(0，100 Hz)。则目标信号的频带为(93.6 Hz,193.6 Hz)，相应的载频为93.6 Hz。噪声强度估算约为0.000 23。势垒调节步长相应设置为1×10-8，得到最优势垒高度和势阱间距参数对为(0.8×10-7，1.13×10-4)。将PFCPs对代入SR模型式(15)，得到图19的系统响应时域、频域图，在频率10 Hz处具有明显的谱峰。图20为频域信息恢复后的时域、频谱图，可发现在103.5 Hz和195 Hz处都出现了明显的谱峰，可认为是被保持架频率调制后的滚动体故障信号，即可判定滚动体故障的存在。

(a)

(b)

5 结 论

利用SR理论检测微弱信号时，为使系统达到SR而产生最佳的输出，不可避免地涉及到系统参数调节。

(a)

(b)

(a)

(b)

而系统参数a或b的调节都会引起势函数特征(势垒高度和势阱间距)的变化，因此不便于直观地了解PFCPs的变化对SR的影响。

(1) 通过PFCPs的引入，提出了基于势垒高度h和势阱间距w调节的SR方法。依照Kramers逃逸速率与目标信号频率的匹配关系，以系统输出信噪比为评价指标，通过调节势垒高度参数h，得到最优的参数对(h，w)，使系统输出响应达到最佳值。

(2) 为了克服采样频比对传统SR的限制，本文给出了基于滤波器技术的时域换频方法，实现了低采样频比的信号检测。动车转向架轴承内圈、外圈以及滚动体故障实验检测研究表明，采用换频技术和PFCPs调节的SR信号检测方法，可以对噪声干扰中的故障信号进行有效检测，验证了本文所提出方法的可行性与有效性。