复杂地形影响下四川省逐月气温空间插值方法研究

何 鹏，蹇东南，李 晓，林正雨 （1.四川省农业科学院农业信息与农村经济研究所，四川 成都610066；.四川省农业科学院大数据中心，四川成都 610066；3.四川农业大学资源学院，四川成都 611130）

随着生态学、农业科学、资源环境科学等相关学科的发展，气候信息在区域和全球尺度变化研究中发挥着重要作用，特别是各类生态系统模型、作物模型都需要空间化的气候要素，并且所要求的时间和空间分辨率也越来越高。例如，在全球变化研究中，景观、区域、全球尺度的生态系统模型，如山地小气候模拟模型（Mountain Microclimate Simulation Model，MT-CLIM）、森林生态系统模拟模型（FOREST-BGC）等，都需要空间化的气温、降水、太阳辐射等环境因子作为输入参数[1]。因此，利用现有的地面气象观测资料和相关技术开发空间化的气候数据产品成为近年来生态学、农业区划、资源和环境科学研究的重点任务之一[2-5]。

在某些研究区域气象站点分布不均，对于这些区域气象数据只能利用有限的观测数据，借助于空间插值方法通过推算求得。气象要素中气温的空间分布主要受经纬度、大气环流、大山系的走向、地形条件、测站点的海拔高度和下垫面性质（土壤、植被）等要素的影响，其中以海拔高度和地形条件的影响最为显著[6]。一般情况下，随着海拔高度的增加气温下降，但其变化速率因山地性质和气候条件而不同[7]。传统的数学插值模型大多没有考虑地形和海拔等相关因素的影响，插值精度不高，不同插值方法得到的结果也有较大差异，在应用于四川省这类地形地貌复杂的区域案例较少[4，8]。为了对比和分析海拔高度对气温空间分布的影响，提高其空间插值精度，该研究在定量分析经纬度、海拔高度差异对气温空间分布影响的基础上，选择多种插值模型对四川省多年月平均气温进行空间插值，并利用交叉检验法对结果的精度进行评估，探讨适合地形复杂、气象站点相对稀少区域的气候资源空间插值方法。

1 数据与方法

1.1 气温数据

气温数据来自国家气象信息中心建设维护的中 国 气 象 数 据 网（http：//data.cma.cn/）提 供 的1981—2010年30 a逐月气象资料，数据制作时间为2012年，共包括四川省144个国家级地面气象站点，数据质量采用气候界限值、台站极值和内部一致性3种方法进行检查和控制[9]。气象站点的空间分布详见图1。

1.2 数字高程模型

数字高程模型（DEM）来源为国际科学数据服务平台（http：//datamirror.csdb.cn/）申请下载的ASTER GDEM第一版本（V1）数据，数据时间2009年，数据投影为UTM/WGS84，空间分辨率为30 m，空间范围为四川省全域。

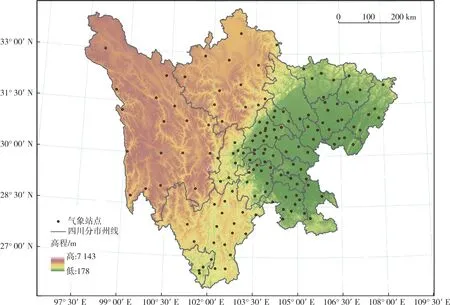
图1 四川省国家级地面气象站点分布Fig.1 Spatial distribution of meteorological stations in Sichuan Province

1.3 插值方法

常用的插值模型有样条函数法（SF）、反距离权重法（IDW）、克立格法（KRGE）等，由于气温随海拔高度增加而降低[7，10-11]，考虑海拔高度影响后的插值结果要优于不考虑海拔高度影响的插值结果，所以进行气温空间插值时海拔高度是附加的重要变量。该研究直接对常用插值模型进行海拔高度修正后插值，再结合多元回归模型插值进行比较。

以144个站点30 a逐月平均气温数据为基础，与各气象站点的经度、纬度和海拔高度数据进行相关性分析。多年逐月平均气温与经度呈正相关，说明四川省平均气温随着经度的增加而升高，这与四川省地势西高东低的总体趋势是一致的，而平均气温随月份波动比较明显，夏季相关系数大于冬季，说明川西高原区与东部平原盆地区的冬季温差要小于夏季温差。多年逐月平均气温与纬度呈负相关，说明四川省平均气温随着纬度的增加而降低。但相关系数随月份波动非常明显，相关系数最大月份是相关系数最小月份的3倍左右，说明四川省北部与南部相比冬季温差要大于夏季温差。以相关系数的绝对值之比来看，四川省平均气温分布在5—10月的经度地带性都远大于纬度地带性，而11—翌年4月的经度地带性与纬度地带性相比并不明显，这可能与四川省位于中低纬度地区（26°～34°N），南北气温差异较小有关。多年逐月平均气温与海拔高度呈负相关，平均气温与海拔高度的相关性随月份波动不大，但也呈现出夏秋季相关性大于冬春季的趋势。

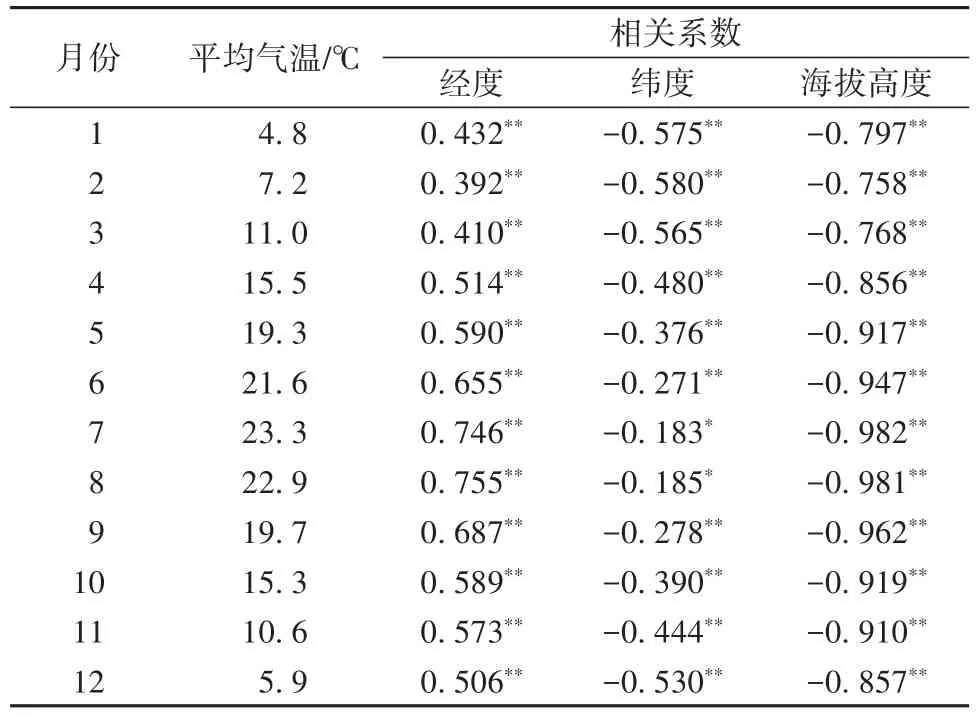
表1 气象站点经纬度、海拔高度与月平均气温的相关性Table 1 Relationship of geographical factors and mean monthly temperature of meteorological stations

1.3.1 样条函数法（spline function method，SP）和加入海拔影响因子的样条函数法（spline function method considering elevation effect，SPE）

样条函数是自然样条函数在二维空间上的推广，使用函数逼近曲面的方法，在空间插值时准确地通过实测样点拟合出连续光滑的曲面[12]。样条函数的估计值计算公式为

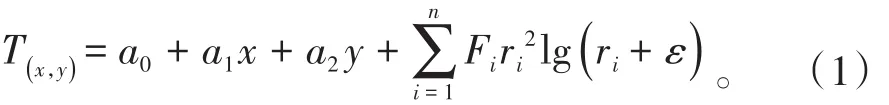
式（1）中，T（x，y）为气象要素的推算值，℃；n为参与插值的台站数；ri为待插值点到第i个气象站点的距离，m；x、y为待插值点的坐标；ε为条件曲面曲率大小的经验参数，一般取10-2～1。Fi、a0、a1、a2为方程系数，由下式计算得到。

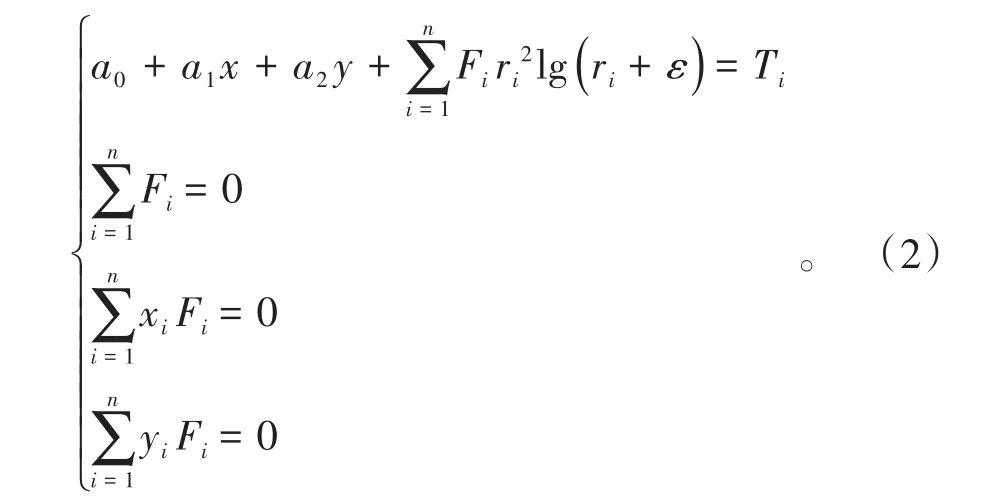
式（2）中，Ti为i点的地面气象观测值；xi、yi为第i个地面观测站的坐标。

考虑了海拔高度影响后，对于网格上任一待插值点，先分别计算各地面气象站点海拔高度与待插值点海拔高度的插值并乘以回归模型中的海拔高度系数，然后分别求其余对应站点要素值的代数和，通过此方法将各台站要素值订正到与待插值点的同一海拔高度上，最后利用样条函数对该网格点进行插值[13]，其计算公式为式（3）～（5）中，Yi为i站气象要素与影响因子的多元回归值；b0为常数项；bk为第k个影响因子的系数；xk为k个影响因子值；Hi，j为待插值点的海拔高度，m；Hk为第k个点的海拔高度，m；β为气温随海拔高度的递减率；W(x，y)为气象要素的推算值，℃。

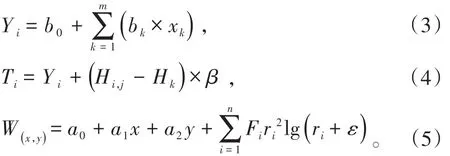
1.3.2 反距离权重法（inverse distance weight interpolation，IDW）和加入海拔影响因子的反距离权重法（inverse distance weighing considering elevation effect，IDWE）

反距离权重法是对采样点进行线性的加权来决定输出的栅格值，加权值与距离成反比，采样点离输出栅格越远，对输出栅格的影响越小。反距离权重法的表达式为

式（6）中，Ti，j为待插值的网格点要素值；Tk为第k个点的要素值；k为第k个被引用到的插值点；dk-2为第k个点到待插值点距离平方的倒数。

考虑了海拔高度影响后，由于气温随着海拔高度增高而降低，进行气温空间插值时，海拔高度是附加的重要变量[13]，其计算公式为

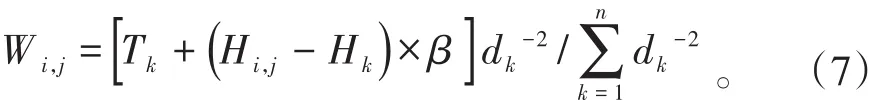
式（7）中，Wi，j为考虑海拔高度影响后气象要素的推算值，℃。

1.3.3 普通克立格法（ordinary Kriging）和加入海拔影响因子的普通克立格法（ordinary Kriging considering elevation effect，OKE）

普通克立格法又称局部最优线性无偏估计法，是建立在变异函数理论结构分析基础之上。所谓线性是指估计值是样本值的线性组合，即加权线性平均；无偏是指理论上估计值的平均值等于实际样本值的平均值，即估计的平均误差为0，最优势指估计的误差平方差最小。计算公式为

式（8）中，Z(ti，j)为待插值的栅格点要素值；Z(tk)为第k个点的要素值；λk为权重系数，其和等于1。

加入海拔影响因子的普通克立格法基于普通克立格法并充分考虑了海拔因子的影响[13]，其计算公式为

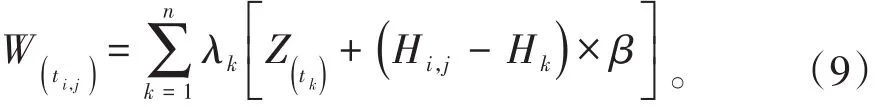
1.3.4 多元回归分析法（multivariable linear regression method，MRM）

多元规划分析模型是应用数理统计方法，建立气象要素与影响气象要素空间插值因子的多元回归模型。在该研究中是建立基于经度、纬度和海拔高度的多年平均气温多元回归模型，并计算残差[2]。

多元规划分析模型表达式为

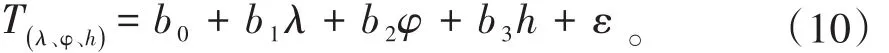
式（10）中，b0为常数；b1、b2、b3为待定系数；λ为经度；φ为纬度；h为海拔高度，m；ε为残差。

1.3.5 气温垂直变化率

气温垂直变化率计算公式为

式（11）中，Ci为各月平均气温，℃；at为回归系数；bi为残差；i为月份，i=1，2，…，12。

1.4 数据处理

利用地理信息系统软件ArcGIS 10.1的数据管理模块（Data Management Tools）、转换模块（Conversion Tools）、地统计模块（Geostatistical Analyst Tools）和空间分析模块（Spatial Analyst Tools）进行数据预处理和插值。属性数据的处理采用SPSS 2.0软件。

（1）参考游松财等[6]提出的气温垂直递减法。首先，根据海拔高程和气温垂直递减率将各气象站的实测气温订正到虚拟海平面上；其次，运用3种常规插值方法（样条函数法、反距离权重法和普通克立格法）对虚拟海平面上的月平均气温进行空间插值，得到虚拟海平面上的气温空间分布；最后，在GIS软件支持下利用相应的DEM数据和气温垂直变化率进行栅格图层的代数运算，得到月平均气温的空间分布。

（2）利用144个气象站点的经度、纬度、海拔高度和多年平均气温数据，在SPSS 20软件中进行多元回归分析，拟合出回归模型（MRM）。将四川省DEM数据在ArcGIS 10.1软件中生成属性值分别为经度（x）和纬度（y）的栅格图层，使用栅格计算器根据回归模型生成多年平均气温栅格图。

表2 地面气象站逐月气温与各地理要素的关系Table 2 Regression equation of geographical factors and monthly temperature of meteorological stations

1.5 模型验证

在使用气象站点数据进行气候指标插值结果的精度检验时，交叉检验（cross-validation）是最常用的一种方法。该方法假设某一个气象站点的气温未知，用其他所有气象站点来估算该气象站点的气温，通过计算所有气象站点的实际气温值与估算值之间的误差来评判空间插值方法的精度。对不同的插值方法，交叉验证可准确验证不同插值方法之间的相对精度，使用时一般用平均绝对误差（MAE，EMA）和均方根误差（RMSE，ERMS）作为检验精度的标准。MAE反映样本数据估值的总体误差或精度水平，RMSE则反映样本数据的估值灵敏度和极值[8]。计算公式分别为

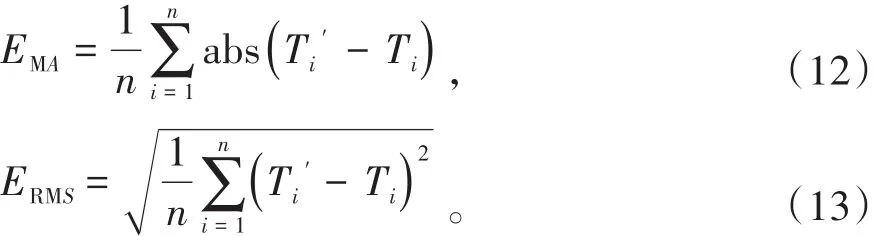
式（12）～（13）中，Ti表示第i个气象站点的实际多年平均气温，℃；T'i表示空间化后第i个气象站点所在栅格单元的气温，℃；abs为求绝对值函数。

2 结果与分析

2.1 月平均气温随海拔高度的变化

一般情况下，在对流层范围内气温随海拔的升高而降低，海拔每升高100 m，气温下降约0.65℃，但是气温的垂直递减率因地点、季节和昼夜气候条件等因素的不同而变化[10]。将各测站点气温随海拔变化这一现象定义为气温垂直变化率，根据四川省144个气象站的海拔高度和30 a月平均气温资料，计算四川省30 a各月地面测站点平均气温垂直变化率，分布区间在0.308～0.443 ℃·hm-2之间，具体计算结果见表3。

四川省多年逐月平均气温与海拔高度呈负相关，平均气温与海拔高度的相关性随月份波动不大，夏秋季大于冬春季，说明四川省平均气温受地形影响极大，垂直地带性明显，在气象数据空间化过程中应该对地形地貌这一影响因子开展更多研究。

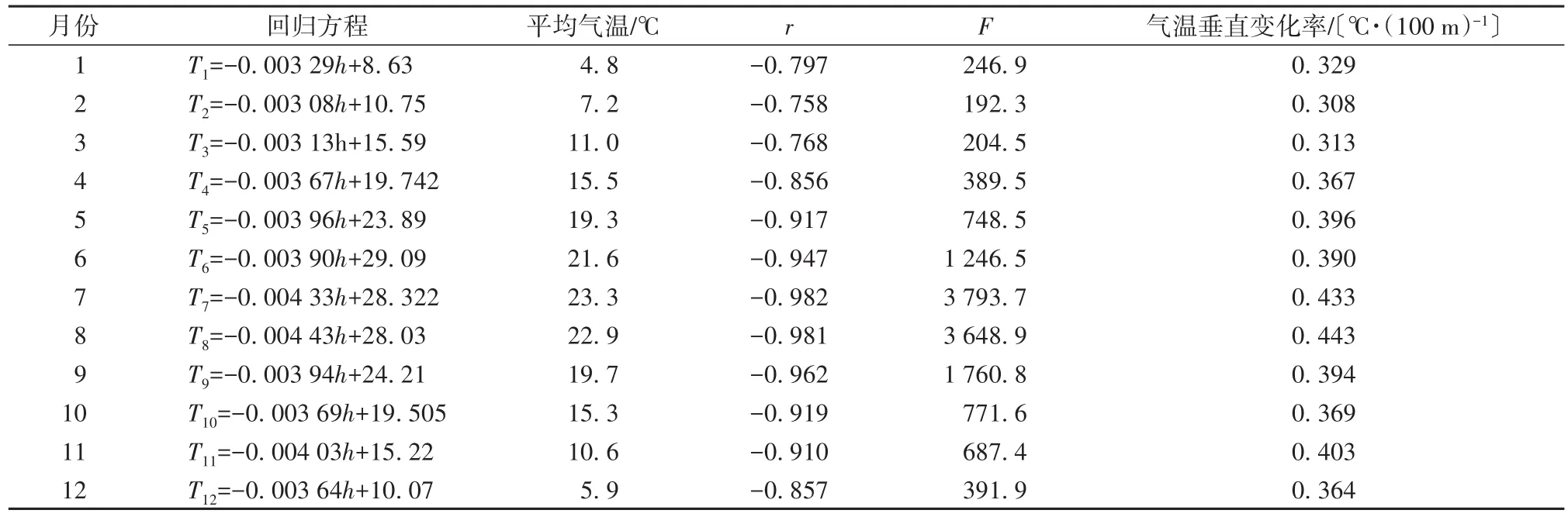
表3 气象站逐月气温随海拔高度的变化Table 3 Regression relationship between monthly temperature and altitude of meteorological stations

2.2 误差分析

基于MAE和RMSE的交叉检验方法，采用常规的SP、IDW、OK插值方法、加入海拔影响因子的SPE、IDWE、OKE和MRM插值方法对四川省1981—2010年144个气象站点的月平均气温空间插值。结果表明：3种常规插值方法中，精度从大到小依次为IDW＞OK＞SP（图2）。其中IDW方法对月平均气温插值的平均EMA为0.96℃，平均ERMS为1.53；OK方法对月平均气温插值的平均EMA为1.29℃，平均ERMS为2.00；SP方法对月平均气温插值的平均EMA为1.87℃，平均ERMS为3.70。因此在不考虑海拔高度影响时仅IDW方法插值的EMA小于1℃，可以用于月平均气温插值，但误差仍然较大，而SP和OK方法误差太大，不能用于月平均气温插值[2]。IDW方法对冬季（11月、12月、1月）的平均气温插值效果最好，其余季节差异不大。SP和OK方法对下半年（6—12月）的平均气温插值效果普遍好于上半年（1—5月），其中6—9月插值效果又略好于10—12月。

图3表明，加入海拔影响因子的SPE、IDWE、OKE和MRM对平均气温的插值精度均明显优于常规的插值方法，精度从大到小为MRM＞IDWE＞OKE＞SPE。以典型的1月（代表冬季）、4月（代表春季）、7月（代表夏季）、10月（代表秋季）作比较，4种加入海拔因子的方法对夏季和秋季平均气温的插值效果均好于冬季和春季，其中以夏季（6—8月）插值效果最好。相比常规IDW方法，加入海拔因子的IDWE方法对月平均气温插值精度提高0.11～0.46℃，对月平均气温插值的平均EMA为0.72℃，平均ERMS为1.09℃；OKE方法对月平均气温插值精度比OK方法提高0.42～0.58℃，对月平均气温插值的平均EMA为0.80℃，平均ERMS为1.12；SPE方法对月平均气温插值精度比SP方法提高0.71～1.04℃，对月平均气温插值的平均EMA为0.97℃，平均ERMS为1.57℃；MRM对月平均气温插值的平均EMA为0.65℃，平均ERMS为0.96℃，精度最高。

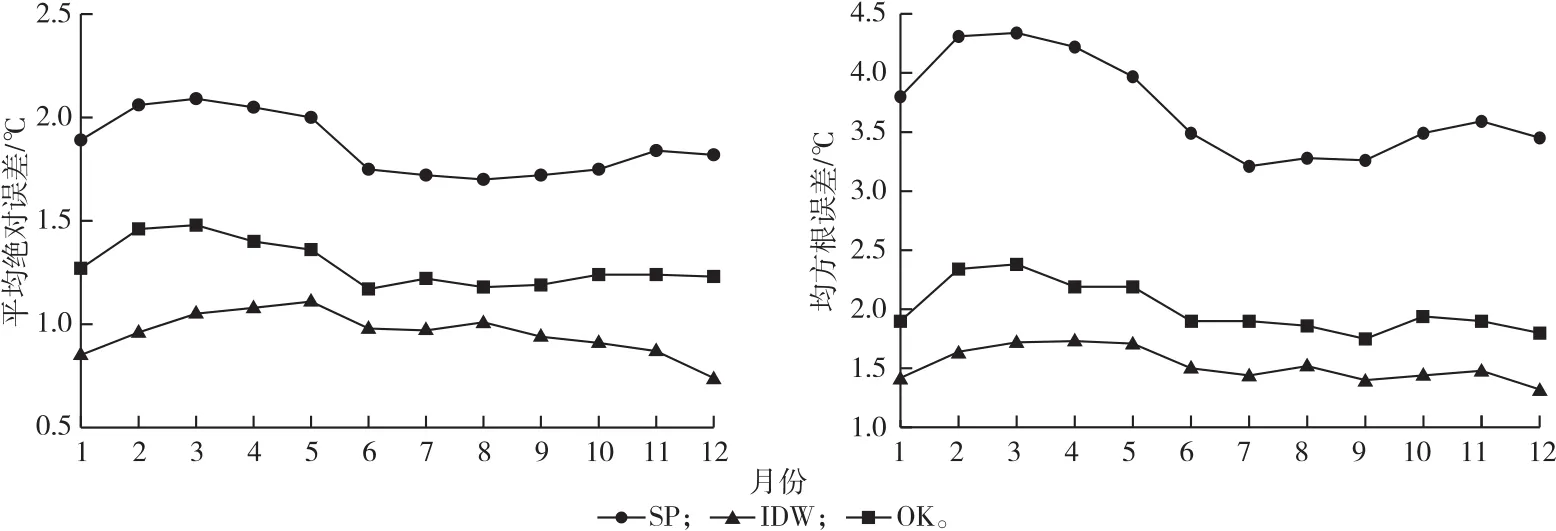
图2 不考虑海拔影响下3种插值方法的平均绝对误差和均方根误差的对比Fig.2 Contrast results of cross-validation error about 3 models without considering elevation effect

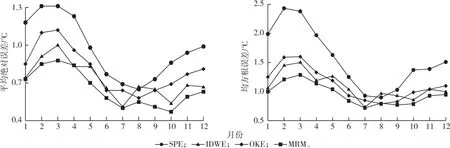
图3 考虑海拔影响下4种插值方法的平均绝对误差和均方根误差的对比Fig.3 Contrast results of cross-validation error about 4 models considering elevation effect

2.3 月平均气温的空间分布

以1月和7月平均气温为例，把常规的SP、IDW和OK这3种方法插值后得到的分辨率为500 m×500 m栅格数据作图（图4）。3种方法空间插值的1月气温范围分别为-11.7～13.6、-23.1～18.6和-14.5～11.9℃，温差跨度极大，低温区主要分布在川西北地区和部分川西地区，高温区主要分布在川南地区，气温分布由低向高略呈西北—东南方向梯度变化；主要受川西高原海拔的影响，气温分布表现出一定的纬度地带性。3种方法空间插值的7月气温范围分别为9.0～27.4、2.5～33.0、7.2～27.3 ℃，温差小于冬季，高温区主要分布在川东、川南的盆周丘陵山区和川中丘陵区，低温区仍然为川西高原的甘孜和阿坝州，气温分布由低向高开始出现一定的西—东方向梯度变化。无论是1月还是7月，样条函数和反距离加权2种方法插值结果均出现了“牛眼”现象，而普通克立格方法插值结果则比较平滑，但反距离加权方法插值在川西高原部分的分布与四川省气候区划[14]一致性较好，普通克立格插值由于平滑过多，与实际气温分布和气候区划差异较大。

以1、4、7和10月平均气温为例，加入海拔因子后把SPE、IDWE、OKE和MRM这4种方法插值后得到的分辨率为500 m×500 m栅格数据作图。由于考虑了海拔影响，无论采用哪一种空间插值方法都能体现出气温随地形特征变化的趋势，与实际气温分布较为贴近，4种插值方法下的1月平均气温分别为-21.2～19.4、-14.2～14.2、-16.9～13.1和-15.6～14.4 ℃，温差跨度极大，4种插值方法下的7月平均气温分别为-3.2～28.3、-2.8～27.9、-2.9～27.8 和-3.4～27.9℃，温差小于冬季。以精度最高的MRM方法制图为例（图5），1月全省气温高值区出现在东部四川盆地区和西南金沙江流域沟谷区域，最高温出现在攀枝花市内金沙江流域，气温低值区出现在川西高原区，最低温出现在甘孜州雀儿山和贡嘎山，气温分布由低向高略呈西北—东南方向梯度变化，主要受川西高原海拔的影响，同时表现出一定的纬度地带性；7月全省高温区域主要出现在川东、川南的盆周丘陵山区和川中丘陵区，最高温出现在广安市、达州市下辖的渠江和嘉陵江流域，低温区域仍然为川西高原的甘孜和阿坝州，最低温出现在甘孜州贡嘎山。

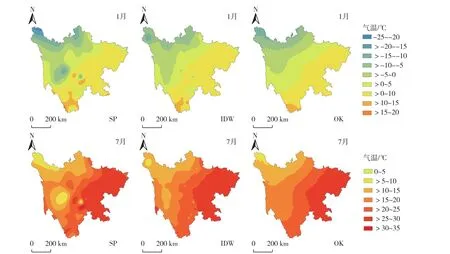
图4 不考虑海拔高度影响下四川省1月和7月平均气温空间分布Fig.4 The spatial distribution map of monthly mean temperature in Januray and July in Sichuan without considering ele‑vation effect

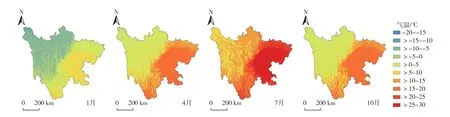
图5 考虑海拔高度影响下四川省不同月份多元回归分析法（MRM）插值的平均气温空间分布Fig.5 The spatial distribution map of monthly mean temperature of different months in Sichuan Province considering elevation effect under MRM method

3 讨论与结论

四川省1981—2010年累年月平均气温与海拔高度之间呈显著相关关系，各月平均气温随海拔高度的增加均呈递减趋势，但是递减幅度不同。四川省夏季月平均气温随海拔高度增加而降低的幅度明显大于冬季，各月平均气温的垂直变化率在0.308～0.443℃·（100 m）-1之间；且相关性呈现明显的季节性变化，夏季月平均气温与海拔高度之间的相关系数大于冬季[15]。以MAE和RMSE来评价插值精度，不同插值方法的夏季EMA值均为0.5～0.7℃左右，明显高于冬季。考虑地形因子的插值结果明显好于不考虑地形因子影响的插值结果。在考虑海拔高度影响的4种空间插值方法中，MRM精度最好，其次是OKE和IDWE，SPE最差。

GIS技术和数学插值方法为气象要素的定量空间分布研究提供了很好的技术手段，但是，如何根据气象站点的数目、空间分布和不同气象要素的特点等选择合适的空间插值方法是非常值得研究的。没有绝对最优的空间内插方法，必须对所研究的区域和数据进行探索性分析，再根据当地特点选择最优的方法[16]。由于现有的国家气象站点地理坐标仅精确到分，实测海拔高度和从30和90 m DEM中提取的其所在位置海拔高度有较大误差，会降低插值精度，这是需要定量研究考虑的。同时该研究仅对4种插值方法的月平均气温插值结果进行了分析讨论，没有将研究区的气象站点按不同海拔高度分别分析其插值精度，进而阐明复杂地形对插值方法选择的影响，这些都是未来需要深入研究的内容。