限位器及车门过档力计算浅析

宋敏鹏，王迎新，张云峰

限位器及车门过档力计算浅析

宋敏鹏，王迎新，张云峰

（众泰汽车工程研究院，浙江 杭州 310018）

车门是使用频率最高的汽车系统之一，用户在开关门时，对车门过档手感会有直接的体验，好的手感可以提高用户满意度、提升品牌形象。过档手感主要由车门限位器提供，但与把手位置、车门重力、铰链等都有重要关联。文章分析了把手位置、车门重力、铰链、限位器等对开关门手感的影响，并详细介绍了车门过档力的计算方法，尤其是限位器过档力矩的计算，对车门过档力的设计和调整，提供了可靠的理论依据。

限位器；开关门手感；车门过档力；限位器过档力

1 前言

新车型开关门手感的确定，通常做法是试制阶段进行实车评审确认，如不满意，则不断对限位器进行实物更改，然后再次评审，直到达到预期效果。这个过程，一般需要3~5轮的修改才可实现，周期长、效率低。造成这种现象的主要原因，一是设计前期缺乏系统的计算，未对限位器进行合理的力矩设计；二是实物评审调整阶段，每次调整限位器时，大多依靠经验，未进行必要的系统性计算确认。因此，合理的车门过档力计算方法，可以大大提高车门限位器开关门手感开发的效率。

2 车门开关门过档力影响因素

车门开关时的过档力，通常以车辆水平放置状态进行评价，其与把手位置、铰链内阻、铰链倾角、车门重量、限位器等均有直接关系。

2.1 把手位置

车门把手是人开关车门的直接操作部位，把手到铰链轴线的距离即为操作力臂，同样的开关门阻力，力臂的长短决定了用户感受到的力的大小，因此，讨论开关门过档力时必须考虑把手的位置。但对一个具体的车型来讲，把手的位置通常是固定的，是不可改变位置的，不能通过调整把手位置来调整过档力。

2.2 铰链内阻

铰链连接着车门和车身，车门开关均绕铰链轴线进行，铰链旋转时自身有一定的内阻，会对开关门手感产生一定的影响。

2.3 铰链倾角

为了使车门具有自动关门的趋势，铰链布置时一般具有一定的内倾角和前后倾角，铰链倾角会使车门重力在开关门方向产生分力，重力分力会直接影响开关门手感。铰链布置是车门各附件布置的基础，影响重大，因此铰链确定以后，通常不会通过调整铰链的方式来调整过档力。

2.4 车门重量

对于铰链倾角已确定的车型，车门重量的大小，决定了重力分力的大小。一般对于具体的车型，各车门的重量为定值。

2.5 限位器

限位器具有控制车门开度、提供过档手感的功能，是开发者调整开关门过档力的最主要手段，即通过调整限位器自身的过档力，来实现车门系统过档力的调整。具体通过调整限位器臂上各斜坡高度、斜度、圆角大小来实现，极少数情况也会调整弹簧的弹力。

图1 限位器示意图

3 车门开关门过档力计算方法及应用

人在开关门过程中，需要克服的阻力矩有：铰链自身的旋转阻力矩M铰、限位器的阻力矩M限、车门重力的分力矩MG，如图2所示。因此根据力矩平衡原理，可知开关门操作力矩MF：

开门时：M=铰+限+M

关门时：M=铰+限-M

图2 车门受力示意图

3.1 开关门操作力矩

人开关门时，通过车门把手进行操作，操作力矩为：

M=*

其中，F为人开关门时使用的力，即开关门过档力，为用户开关门时的直接感受；

L为对应的力臂，即把手到铰链轴线的距离。

3.2 铰链自身的旋转阻力矩

铰链作为一个单独的零部件，其自身旋转存在内阻，阻力矩一般为固定的范围，计算时可取中值，即针对特定的车型，铰链自身的旋转阻力矩为定值。

3.3 车门重力的分力矩

因为铰链轴线存在倾角，车门重力在开关门方向上存在分力，其大小为：

G=*cos

其中，P为过重心且垂直于铰链轴线的平面；

GP为重力在平面P上的分力；

G为车门重力

A为重力G与平面P的夹角，针对具体车型则为恒定值。

车门重力分力GP在开关门方向产生的力矩为：

M=G*L*sinB

其中，LG为车门重心到铰链轴线的距离。

B为重力分力GP与重心铰链连线LG的夹角，∠B随车门开度变化而变化，因此每个档位需分别计算（注：重力分力GP在重心铰链连线LG的车内侧时为正，否则为负）。

图3 车门重力分力矩示意图

3.4 限位器的阻力矩

3.4.1 限位器弹簧弹力计算

限位器自身的过档力，由限位器滑块在限位器臂上爬坡时，压缩限位器弹簧产生。限位臂两侧各有一个弹簧，结构对称，故两弹簧的总弹力为：

弹= 2**△

其中，K为弹簧的弹性模量；

ΔL为单个弹簧的压缩量。

如图4所示，根据限位器的结构特点，弹簧压缩量可表示为：

△=0-（H-H1-t）

其中，L0为弹簧自由状态下长度；

H为限位盒闭合高度；

H1为滑块上弹簧配合端面，到滑块与限位臂切点的距离；

t为滑块与限位臂切点，到限位臂中心平面的距离。

图4 弹簧压缩示意图

如图5所示，根据限位器滑块的结构特点，尺寸H1可表示为：

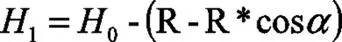
其中，H0为滑块上，弹簧配合端面到限位臂配合端面的厚度；

R为滑块圆角半径；

𝛼为法线与竖直方向的夹角。

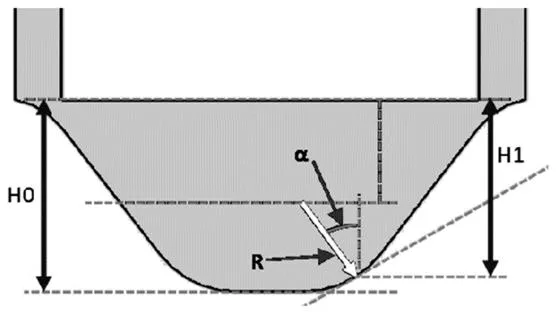
图5 滑块端部示意图

如图6所示，根据限位器臂斜坡的弧度走势，可知最大过档力必然出现在顶部圆角区域内，此时尺寸t可表示为：

其中，r为限位臂凹坑顶部圆角半径；

h为圆角r的圆心到限位臂中心平面的距离（注：圆心在限位臂中心线下方时为正，否则为负）。

图6 限位臂斜坡局部示意图

综合上述分析，两弹簧总弹力可表示为：

式中，仅角度𝛼随滑块爬坡高度而变化，其他均为定值。

3.4.2 限位器沿限位臂方向拉力计算

滑块在限位臂上爬坡时，弹簧弹力为竖直方向的力，部分力转换为水平运动方向的阻力，滑块运动方向的拉力F拉需克服该阻力，其受力分析如图7所示。

图7 滑块上坡时受力分析示意图

根据受力平衡，有：

其中，FN为滑块受到的支持力；

f为滑块受到的摩擦力；

μ为摩擦系数。

据此可推导出以下公式：

在有润滑脂条件下，滑块（POM）与限位器臂（PA66）的摩擦系数较小，所以通常在计算时，会忽略摩擦力的作用，故上式又可表示为：

3.4.3 限位器合力计算

开关门时，限位器不仅有滑块沿限位臂方向的运动，还有限位盒、限位臂绕轴线旋转的运动，其受力过程可简化为图8模型：

图8 限位器合力与分力关系示意图

图中：

O：铰链轴线；

A：限位器旋转中心；

B：初始状态的限位盒中心点；

B’：为任意档位时的限位盒中心点位置；

b：限位盒中心点到铰链轴线的距离，为定值；

c：限位器旋转中心到铰链轴线的距离，为定值；

β：限位盒中心点和铰链轴线连线，与限位盒安装面的夹角，为定值；

γ：初始位置时，限位盒中心点和铰链轴线连线OB，与限位器旋转中心和铰链轴线连线OA的夹角，为定值；

λ：任意档位时的开门角度；

F合：限位器合力；

F拉：F合在沿限位臂方向上的分力；

F旋：F合在限位臂旋转方向上的分力。

由图可知，限位器合力F合与沿限位臂方向拉力F拉的关系为：

又因：

故：

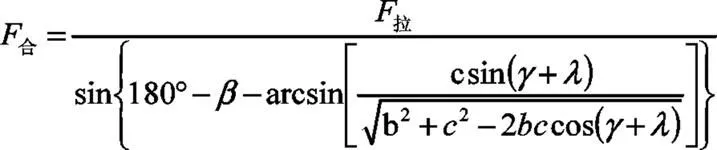
式中，限位器合力F合与沿限位臂方向拉力F拉的关系，仅与开门角度λ有关，代入各个档位的开门角度即可。

3.4.4 限位器阻力矩计算

如图9所示，限位器阻力矩为：

其中，L限为当前档位时的限位器力臂。

3.4.5 车门及限位器过档力设计应用

上文详细介绍了车门过档力的计算方法，开发者在前期数据设计阶段，需首先确定车门各个档位时的开关门力目标值，然后根据该方法确定限位器自身的过档力，即确定限位器臂各档位斜坡的弧度特征。然后在试制阶段，对实车的开关门手感进行确认，如需调整，则根据过档力实测值，对目标值进行修正，再根据计算调整限位器臂特征。需特别注意的是，零部件实际质量往往与前期设计时的预估值存在一定的差异，试制阶段需对车门的实际重量进行确认修正。

4 结论

本文主要从开关门过档力的影响因素出发，系统的阐述了开关门时的受力情况，并详细介绍了人手操作力矩、铰链自身阻力矩、车门重力分力矩、限位器阻力矩的计算方法和应用时的注意事项。此系统涉及多个零部件，运动关系和受力情况复杂，通过本文的介绍，可以给从事相关专业的开发者们提供合理的参考帮助。

[1] 胡峥楠,刘天才,汤小生.汽车开关门手感及声品质提升[J].汽车工程师,2018(10):43-45.

[2] 任帅,石小强.车门限位器布置与设计[J].轻型汽车技术,2016(9/10): 14-17.

[3] 靳龙,曾昊,李玉奇.某型汽车车门限位器结构及布置设计[J].广西科技大学学报,2016,第27卷第4期:21-24.

[4] 董艳菊,洪兵,刘春达等.车门限位器布置与设计初探[C].2010中国汽车工程学会年会论文集,北京:机械工业出版社,1154-1160.

[5] 丁光学.限位器臂杆结构与侧门限位能力的计算应用[J].科技创新与应用,2016(9):11-13.

[6] 雷学明,班正逸,周利民.车门限位器布置设计[J].汽车实用技术, 2014(1):29-32.

Calculation Analysis of Check's Operation Force

Song Minpeng, Wang Yingxin, Zhang Yunfeng

( Zotye Automobile Engineering Research Institute, Zhejiang Hangzhou 310018 )

Door is one of the most frequently used systems in the vehicle. When users open and close the door, they will have an intuitive feelings through the check's stop. A comfortable experience can improve customersatisfaction and enhance brand image. The experience is mainly provided by the check, but is also significantly related to the handle position, door gravity, hinges, etc. This paper not only analyzes the influence of handle position, door gravity, hinge and check, but introduces the calculation method of the door's operation force in detail, which includes the calculation of the check's resisting moment. It provides a reliable theoretical basis for the design and adjustment of the door's opening and closing feel.

Check; Door’s opening and closing feel; Door's operation force; Check's operation force

U463.83+4

A

1671-7988(2019)13-79-04

U463.83+4

A

1671-7988(2019)13-79-04

宋敏鹏（1989-），男，主管工程师，先后就职于奇瑞汽车股份有限公司和浙江众泰汽车制造有限公司杭州分公司，主要从事汽车开闭件和附件系统的设计研发工作，对门系统的开发工作有着较为丰富的经验。

10.16638/j.cnki.1671-7988.2019.13.028