我国流通业全要素生产率测算及其影响因素实证研究

陈薛 李照作

内容摘要：流通业在推动我国社会经济发展方面起到了至关重要的作用。近年来流通业全要素生产率（简称TFP）测算以及影响因素成为了学术领域重点研究课题。文章运用索洛残值法测算了2000-2016年我国31个省市的流通业TFP构建空间计量模型，并对流通业TFP的影响因素进行实证分析。研究结果表明：我国各省的流通业TFP具有明显的空间相关性和空间异质性;地理环境因素对流通业TFP的影响显著，地理位置相邻地区的流通业TFP具有趋同现象;硬件设备以及工业化发展进程对流通业TFP的提升有着显著正相关影响作用，而市场需求条件以及市场化水平的促进作用不显著。

关键词：流通业   全要素生产率   空间计量模型   影响因素

研究背景

流通业作为我国重要的支撑行业，在拉动周边产业发展、推进社会经济发展以及解决社会就业问题方面有着至关重要的作用。R.M.Solow作为第一个提出全要素生产率的研究人员，对经济发展中无法被劳动、资本解释的内容，利用“索洛余值”法对全要素生产率进行了推算。二十世纪八十年代，研究人员Dale W. Jorgenson通过超越对数生产函数的模式对生产率进行了测算，完成了测算TFP过程中投入要素的精准计算。随着学术界对我国流通业实践及理论研究的进一步开展，如何精准计算我国的流通业全要素生产率成为研究热点。在此背景下，本文對我国流通业全要素生产率进行了具体研究。

我国流通业TFP的测算及分析

（一）变量选取及数据说明

变量选取。目前学界对“流通业”这一概念没有形成统一认识，由于我国交通运输、仓储、邮政业增加值占据整个流通行业增加值的百分之八十以上，故本文选取交通运输、仓储以及邮政业数据作为主要研究对象。

产出指标。本文以交通运输、仓储以及邮政业的生产产值作为我国各地区流通业的产出参数，并结合各地区对应年份的价格指数针对当年名义值展开平减，并将其折算为2000年的固定价格。

资本投入规模。本文以我国各地区交通运输、仓储、邮政业固定资产投资额度为基础数据，并利用固定资产投资流量数据和永续盘存法，将2000年固定价格在各地区各个年份的流通业资本存量进行有效推算。计算公式为：Kit =（1-）K i （t-1）

+Iit。在计算公式中，Kit代表i地区在t期间资本存量，Ki（t-1）代表i地区t-1期间的资本存量;iit所代表的是i地区在t期间的流通业投资额度，以固定资产价值指数为基础，实现价值指数折算，继而明确2000年固定价格;指的是折旧率，折旧率假设为5%。据国际惯用的方法计算基期年的资本存量（Ki0），Ki0=Ii0 /（g+）。上述公式中g代表样本期实际投资的年均值，Ki0所代表的是i地区基期年资本存量，Ii0所指的是i地区流通行业固定资本额度。

劳动投入规模。按照规定劳动强度的劳动时间和劳动报酬选择劳动投入规模。由于相关数据可通过互联网获取，故劳动投入参数主要以国内各个省份运输、仓储、邮政业的劳动人员数量作为衡量依据。

数据说明。结合数据的可获取性和实证研究需要，本研究选择2000-2016年间我国31个省份地区的数据作为研究对象。数据主要来源于《中国统计年鉴》（2001-2016）、各省统计年鉴（2001-2016年）数据、中国经济信息网数据等。

（二）生产函数模型

TFP所代表的是技术与管理水平逐步提高下对经济增长的贡献值，其中不包括资本要素、劳动要素投入所存在的影响。现阶段对TFP的计算主要通过数据包络分析法（简称DEA法）、SFA法等多种方法共同应用而实现。本研究通过SR法对我国31个省市的流通业展开TFP计算分析。假设在流通业生产函数中，主要投入的要素为资本要素与劳动要素，此时得出的生产函数公式应为：

公式（1）中，αik表示i地区，αil表示劳动的产出弹性值;αit表示i地区流通业TFP弹性指数;Ai0表示i地区流通业TFP;Yit表示i地区t期间流通业产出值;Kit代表地区i在t期间内物质资本要素的投入量;Lit代表地区i在t期间内劳动力要素的投入量。将得出函数公式：

对公式（2）和公式（3）进行回归分析可得出资本的产出弹性值αik，劳动的产出弹性值αil。对上述值进行正规化处理，得出、。则i省t期的流通业TFP为：

（三）流通业TFP核算

由于篇幅有限，本研究只将2000年、2003年、2006年、2009、2013以及2016年作为代表年份进行分析，上述代表年份中我国各个省份地区流通业TFP以及这一时期我国流通业TFP均值以及增长率具体如表1所示。

纵向来看，2000-2016年期间，我国各地区流通业TFP值均实现了稳定增长，但各地区的流通业TFP值年均增长率却有很大差距。2000-2016年，我国流通业TFP年均增长率超出7.5%的地区有江苏、黑龙江、安徽等;在以上流通业TFP年均增长率数据中，处于4.5%-7.5%增长率范围的的地区包括湖南、广东等;流通业TFP年均增长率低于5%的地区包括重庆、山西、北京等。对2000-2016年间我国各个省份地区流通业TFP年均值和TFP年均增长率进行对应研究，可以计算出两者相关系数为0.2143，这表示一些地区虽然TFP值较高，但并不代表该地区的TFP增长率高，对于这一现象政府机构应予以高度重视。

我国流通业TFP影响因素的空间计量分析

（一）影响因素指标的选取

流通业作为我国第三产业，该行业的发展上不仅与所在地区的环境、政治、文化等要素有着直接联系，还与技术、政策等要素息息相关。对此，本文主要选取基础设备、需求条件、工业化进程、市场化程度作为研究对象进行分析。

基础设备。在流通业中，基础设备水平代表着地区流通的供给水平。优良的交通硬件设备可以降低运输成本、提升资源配置水平，从而优化流通业技术水平。在本文研究中，以铁路、公路等流通网络营业里程作为影响区域流通业TFP的基础设备要素。

需求条件。需求主要来自于社会生产、物流及消费过程。在流通需求不断提高的环境下，流通业集聚程度也会逐步提高。因此可得出，流通需求增大有利于推动流通业持续快速发展。本研究以货物周转规模作为影响区域流通业TFP的需求条件要素。

工业化进程。由于流通业是工业化发展的必然产物，故本文将各个地区第二产业增加值占该地区GDP的比重看作是其工业化进程，其单位均为亿元。

市场化水平。市场化有利于提高资源配置率、提升各要素的产出效率，能够在一定程度上推动流通业TFP提高。故本文以全社会规定资产投资中非国有、集体投资占总投资的比重看作是市场化指数，其代表各个省份地区的市场化水平。

（二）空间计量模型

对空间面板数据在具体计算上，主要涉及两大模型的利用，分别为空间滞后模型和空间误差模型。通过两大模型的计算，可获得空间固定效应、时间固定效应，对流通业TFP影响要素的空间面板数据模型进行如下：

在上述模型中，InTFP代表被解释变量，即i省（自治区、直辖市）t期的流通业TFP ;InNFRA、InDEM、InINDU和InMAR表示自变量;C表示截距项;参数β表示被解释变量受到解释变量的影响程度;ρ表示空间回归系数。另外，空间误差系数主要通过λ表示;空间固定效应、时间固定效应分别以η、予以表示;服从正态分布随机误差、空间权重矩阵分别以μ、W予以表示。鉴于空间相关性原则，若传统最小二乘法围绕以上2个模型进行回归分析，则会出现系统误差。由于本研究以这种计算模式对流通业TFP影响要素展开研究，为确保不存在异方差，各项指标均取对数。空间权重矩阵选用二分权重矩阵，其构建方法按照Rook相邻标准“假如两区域存在共同边界那么这两个地区属于相邻关系”。矩阵W设置模式遵循下述条件“主对角线中的元素ωit值是0。假如省份i与省份j相邻，则ωit值等于1，否则等于0”。

（三）空间自相关检验

本文主要以Moran推出的全局空间自相关指数（Morans I指数）和与局部空间相关性指数来整体识别地区之间经济上的空间相关性。

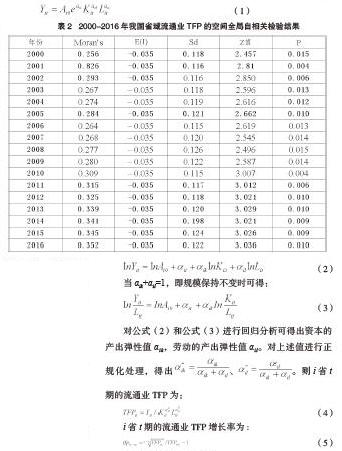
1.全局空间相关性检验。Morans I指数数值处于-1 至1区间范围。假如Morans I指数<0，意味着各个空间经济变量存在负相关关系;Morans I指数=0，意味着个空间经济变量不具备相关性;Morans I指数>0，表示各个空间经济变量之间呈现的关系为正相关关系。表2详细显示了2000-2016年期间我国各省份地区流通业TFP的Morans I指数。由表2可知，2000-2016年间我国各地区流通业TFP的Morans I指数全部大于零，这一指数从2000年的0.256上升到2005年的0. 284，虽然这一指数2000-2005年期间有所下降，但在2006年后呈稳定上升趋势，2016年Morans I指数达到了0. 352。从中可以得知，当前我国各个省份流通业TFP在地理位置方面均能体现空间自相关特性。通过分析2000-2016年间Morans I指数数据可知，数据显著性水平P值均小于5%，这表明2000-2016年间我国各个省份地区流通业TFP的空间自相关性显著为正，观测值空间集聚效应显著。

由表2可知，2000-2016年间我国各地区流通业TFP值存在空间维度的依赖性与差异性。具体而言，当前我国东部、中部及西部地区流通业发展水平存在较大差距，国内流通行业发展水平表现为东高西低，流通业TFP的地区不平衡特性较为显著。

2.空间面板模型估计结果。从Morans I数据结果分析中得出，当前我国多个省份流通业TFP对空间分布方面存在显著自相关特性。由于忽略异质性和空间维度对流通业TFP特征与发展走势进行分析，会导致结论与实际存在明显差异。因此本文对空间要素进行研究时，在计算模型中引入空间要素。由表3可知，空间滞后模型在1%显著水平下通过检验，而空间误差模型没有通过空间依赖性的显著性检验，因此空間滞后模型更为适合。除此之外，根据Hausman检验，以上2种模型都需结合固定效应模型。由于本文研究对象属于样本整体，因此固定效应模型更为合适。为了便于对比，本文对传统面板数据固定效应模、空间滞后模型以及空间误差模型依次进行估算，根据LeSage编辑的程序，以Matlab7.U软件对SLM与SEM展开参数计算，最终得出数据结果如表4所示。

由表4可知，时间固定效应的SLM空间系统ρ并不具备显著特性，而其他模型的空间系数ρ、λ均通过1%显著水平检验，即均具备显著性。此外，时空双固定效应中的SLM、SEM的log似然值相比于传统个体固定效应模型或其他空间模型要更高，这两种模型工业化水平、市场化水平均且不具备显著特性，因此不应选择这两种模型。相比之下，在空间固定效应中，SLM的log似然值相对高，各项即使变量与空间系数相对显著，因此本研究在对流通业TFP影响要素研究上，主要选取空间固定效应模型SLM展开研究。

结论及建议

综上所述，第一，我国各地区流通业TFP空间相关性较为显著。通过对Morans I值分析可以得出，我国东部、中部、西部地区流通业TFP存在较大差异，地区不平衡特性较为显著。为促使流通业一体化发展，政府应基于全局的视角对流通业发展进行设计;第二，地理环境要素对流通业TFP存在显著影响，国内地区流通业TFP存在趋同性。对此，为推动流通业可持续发展，应加强相邻省份之间的合作，从而促进地区间生产要素流通效率提高，进而实现我国经济统筹发展;第三，硬件设备及工业化发展进程对流通业TFP的提升有着显著正向作用，而市场需求条件及市场化水平的促进作用不显著。

参考文献：

1.刘鹏.我国流通经济质量的测度及影响因素研究[J].商业时代，2013（27）

2.孙畅，吴立力.长江经济带流通业全要素生产率增长及行业异质性的实证研究[J].管理现代化，2017，37（1）

3.王健，梁红艳.中国流通业全要素生产率的影响因素及其收敛性分析[J].福州大学学报（哲学社会科学版），2013，27（3）

4.何琴清，吴振鹏，欧欣玲，陈嘉荣.基于DEA的珠三角地区流通业全要素生产率研究[J].商业经济研究，2017（17）

5.何琴清.流通业全要素生产率研究综述[J].物流科技，2016，39（4）

6.王琦.我国区域间流通业全要素生产率的趋同性分析[J].商业经济研究，2015（29）

作者简介：

陈薛（1999-），女，汉族，江苏盐城人，郑州大学公共管理学院2016级本科生，专业方向：人力资源管理。

李照作（1976-），男，汉族，河南郑州人，硕士，郑州大学公共管理学院人力资源管理系讲师，研究方向：政府管理、公共部门人力资源管理。