Further Results on Meromorphic Functions and Their nth Order Exact Differences with Three Shared Values
2019-07-23ChenShengjiangXuAizhuandLinXiuqing
Chen Sheng-jiang, Xu Ai-zhu and Lin Xiu-qing
(Department of Mathematics,Ningde Normal University,Ningde,Fujian,352100)
Communicated by Ji You-qing
Abstract:Let E(a,f)be the set of a-points of a meromorphic function f(z)counting multiplicities. We prove that if a transcendental meromorphic function f(z)of hyper order strictly less than 1 and its nth exact difference ∆ f(z)satisfy E(1,f)=E(1,∆ f),E(0,f)⊂E(0,∆ f)and E(∞,f)⊃E(∞,∆ f),then ∆ f(z)≡f(z).This result improves a more recent theorem due to Gao et al.(Gao Z,Kornonen R,Zhang J,Zhang Y.Uniqueness of meromorphic functions sharing values with their nth order exact differences.Analysis Math.,2018,https://doi.org/10.1007/s10476-018-0605-2)by using a simple method.
Key words:meromorphic function,exact difference,uniqueness,shared value
1 Introduction and Main Results
We assume that the reader is familiar with the fundamental results and standard notations of Nevanlinna’s theory,as found in[1]and[2],such as the characteristic function T(r,f)of a meromorphic function f(z).Notation S(r,f)means any quantity such that S(r,f)=o(T(r,f))as r →∞outside of a possible set of finite logarithmic measure.Given one value a ∈C∪{∞}and two meromorphic functions f(z)and g(z),we say that f and g share a CM(IM)when f and g have the same a-points counting multiplicities(ignoring multiplicities).Denote by E(a,f)the set of all zeros of f −a,where a zero with multiplicity m is counted m times in E(a,f),then f and g share a CM provided that E(a,f)=E(a,g).Moreover,if E(a,f)⊂E(a,g),then we say that f has a partially shared value a CM with g.
About ten years ago,Halburd and Korhonen[3],[4],Chiang and Feng[5]established the difference analogue of Nevanlinna’s theory for finite order meromorphic functions,independently. Later,Halburd et al.[6]showed that it is still valid for meromorphic functions of hyper-order strictly less than 1.So far,it has been a most useful tool to study the uniqueness problems between meromorphic functions f(z)and their shifts f(z+c)or the nth exact differences ∆f(z)(n ≥1).For some related results in this topic,we refer the readers to reference[7]–[11]and so on.
In 2013,Chen and Yi[7]proved a uniqueness theorem for a meromorphic function f(z)and its first order exact difference ∆cf(z)with three distinct shared values CM,which had been improved by Zhang and Liao[11]in 2014,L¨u F and L¨u W R[10]in 2016 and Chen[12]in 2018.In this direction,Gao et al.[13]obtained the following uniqueness theorem concerning the nth exact difference more recently.
Theorem 1.1[13]Let f be a transcendental meromorphic function of hyper order strictly less than 1 such that/≡0.If f(z)andshare three distinct periodic functions a,b,c ∈ˆS(f)with period 1 CM,then≡f(z).
Here,the notation ˆS(f)means S(f)∪{∞},where S(f)is the set of all meromorphic functions α(z)such that T(r,α)=S(r,f).It is obvious that the conditions of sharing values in Theorem 1.1 could be rewritten as“E(a,f)=E(a,∆f),E(b,f)=E(b,∆f)and E(c,f)=E(c,f)”.So,a natural question is:could those conditions of sharing values be weaken?
In this paper,we give an affirmative answer to the above question and prove a more general result compared to Theorem 1.1 by using a simple method which is very different to the proof of Theorem 1.1.That is
Theorem 1.2Let f be a transcendental meromorphic function of hyper order ρ2(f)<1,and let c ∈C{0}such that ∆f(z)/≡0.If
Here,the hyper order ρ2(f)is defined byas usual.Clearly,our result improves Theorem 1.1.
2 Some Lemmas
To prove our result,we need the following auxiliary results.
Lemma 2.1[3],[6]Let f(z)be a nonconstant meromorphic function of hyper order ρ2(f)<1 and c ∈C{0},n be a positive integer.
nThen for any a ∈C,we have

Lemma 2.2Let f(z)be a nonconstant meromorphic function of hyper order ρ2(f)<1,and c ∈C{0}such that ∆f(z)/≡0.Let q ≥2 and a1,,aqbe q distinct finite complex numbers.Then
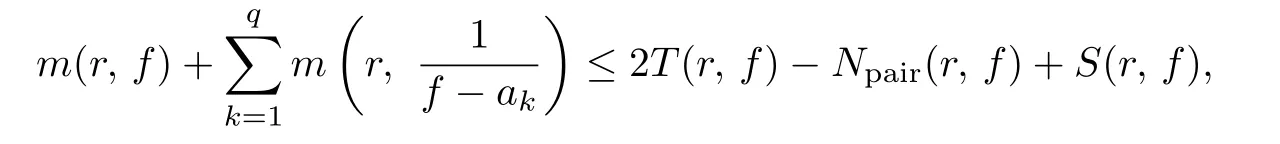
where


where αk∈C.It follows from Lemma 2.1 that
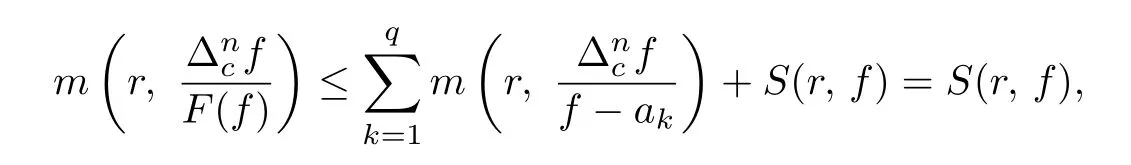
so
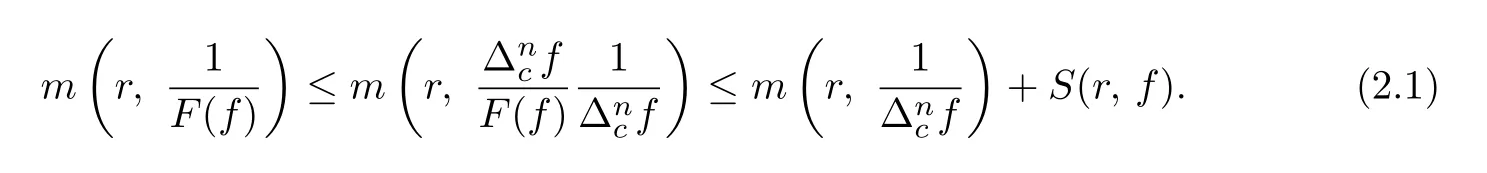
Next,by applying the First Main Theorem and the Valiron-Mo’honko identity(see[11],Lemma 1.3),we deduce from(2.1)that

Hence,it follows from Lemma 2.1 and(2.2)that
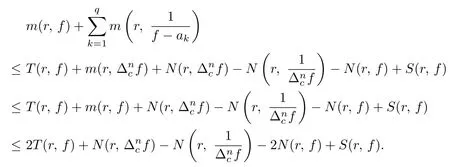
This completes the proof of Lemma 2.2.
Remark 2.1Lemma 2.2 is so called the difference analogue of the Second Main Theorem by replacingwith ∆f,and by replacing aiwith periodic small meromorphic functions ai(z)with period c with regard to f,as found in[3]and[6].Although the proof of Lemma 2.2 is very similar to the proof of the Second Main Theorem,however,Lemma 2.2 plays a key role in the proof of our result in this paper.
To estimate N(r,f(z+c))and T(r,f(z+c)),we need the next result.
Lemma 2.3[6]Let T:[0,+∞)→[0,+∞)be a non-decreasing continuous function and s ∈(0,∞).If the hyper order of T is strictly less than one,i.e.,
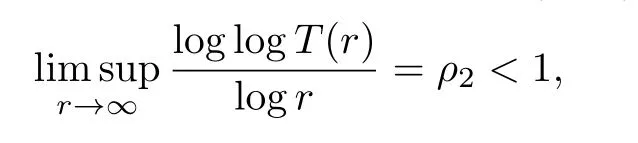
and δ ∈(0,1 −ρ2),then
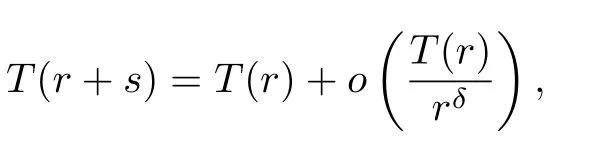
where r runs to infinity outside of a set of finite logarithmic measure.
3 Proof of Theorem 1.2
We firstly prove that T(r,f)and T(r,∆f)can be restricted by each other.According to the assumption E(0,f)⊂E(0,∆f),we have

It follows from(3.1)and Lemma 2.1,we get
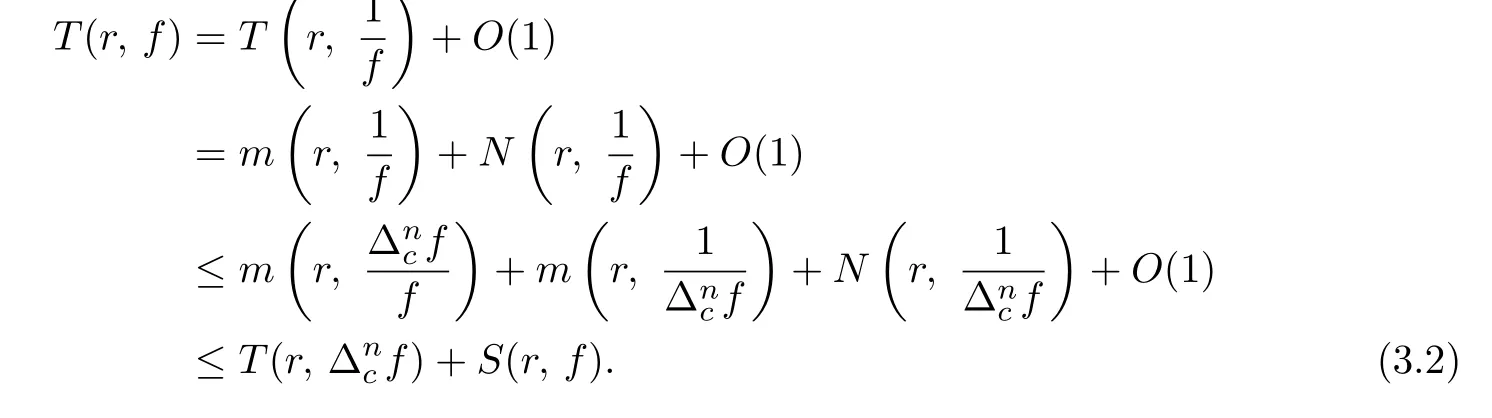
Conversely,by Lemma 2.3.one can get
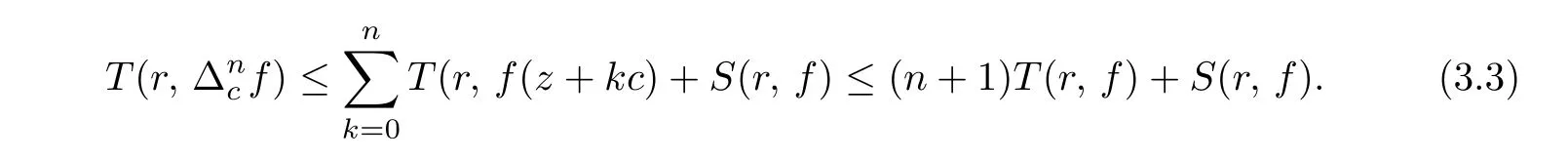
Together(3.2)with(3.3),we have
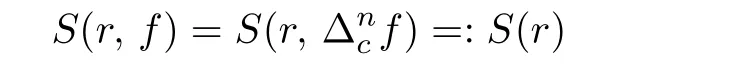
and


Next,we set which implies ρ2(h)<1 due to(3.4).And thus,h is an entire function from the assumptions E(0,f)⊂E(0,∆f)and E(∞,f)⊃E(∞,∆f). What is more,by using Lemma 2.1 again,we have T(r,h)=S(r). (3.6)
Now,we suppose on the contrary that the assertion of Theorem 1.2 is not true,i.e.,∆f /≡f.
We find out a contradiction step by step as follows.


Let z0be a 1-point of f with multiplicity p ≥2.Since that E(1,f)=E(1,∆f),we get from(3.8)that z0is a zero ofwith multipl
icity at least p−1.What follows,we distinguish two cases.
Case 1.Assume that h is not a constant.Noting T(r,)≤2T(r,h)+S(r,h),we know that
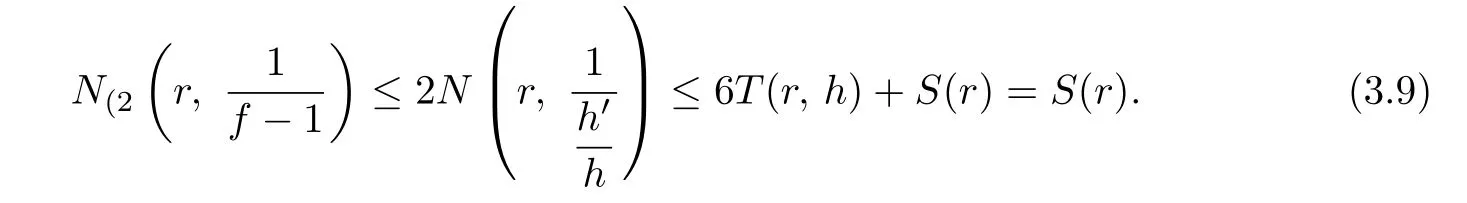
Case 2. Assume that h is a constant.Then,we can deduce from(3.5)that 1 is a Picard value of f under the hypothesis ∆ncf /≡f.Hence,we also have

In any case,from(3.7),(3.9)and(3.10),we can obtain the following conclusion:

Finally,by using the assumptions E(0,f)⊂E(0,∆ncf)and E(∞,f)⊃E(∞,∆ncf)again,we have
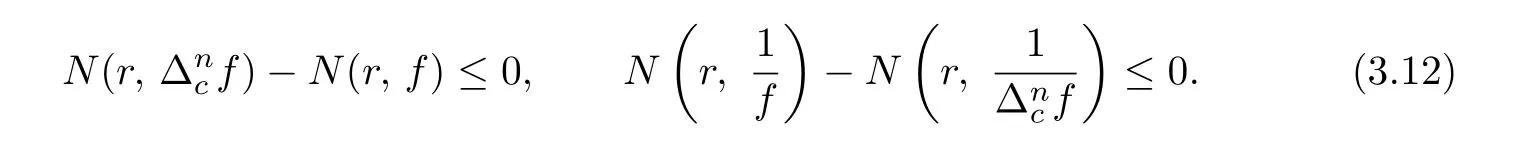
Combining(3.11),(3.12)and Lemma 2.2,we have

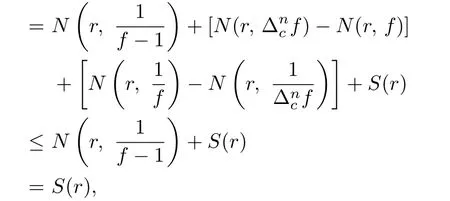
which is impossible.And this completes the proof of Theorem 1.2.
杂志排行
Communications in Mathematical Research的其它文章
- Common Fixed Points for Two Mappings with Implicit-linear Contractions on Partially Ordered 2-metric Spaces
- An Optimal Sixth-order Finite Difference Scheme for the Helmholtz Equation in One-dimension
- Fekete-SzegInequality for a Subclass of Bi-univalent Functions Associated with Hohlov Operator and Quasi-subordination
- The Transfer Ideal under the Action of a Nonmetacyclic Group in the Modular Case
- An SIRS Epidemic Model with Pulse Vaccination,Birth Pulse and Logistic Death Rate
- Planar Cubic G1 Hermite Interpolant with Minimal Quadratic Oscillation in Average
