An Optimal Sixth-order Finite Difference Scheme for the Helmholtz Equation in One-dimension
2019-07-23LiuXuWangHainaandHuJing
Liu Xu, Wang Hai-na and Hu Jing
(School of Applied Mathematics,Jilin University of Finance and Economics,Changchun,130117)
Communicated by Li Yong
Abstract:In this paper,we present an optimal 3-point finite difference scheme for solving the 1D Helmholtz equation.We provide a convergence analysis to show that the scheme is sixth-order in accuracy.Based on minimizing the numerical dispersion,we propose a refined optimization rule for choosing the scheme’s weight parameters.Numerical results are presented to demonstrate the efficiency and accuracy of the optimal finite difference scheme.
Key words:Helmholtz equation,finite difference method,numerical dispersion
1 Introduction
In this paper,we consider the 1D Helmholtz problem(see[1])

with the wavenumber k,where unknown u usually represents a pressure field in the frequency domain,and f denotes the source function.The Helmholtz equation has important applications in acoustic,electromagnetic wave scattering and geophysics.As the solution of the Helmholtz equation oscillates severely for large wavenumbers,it is still a difficult computational problem to develop efficient numerical schemes to solve the Helmholtz equation at high wavenumbers.
To numerically solve the Helmholtz equation,there are mainly finite difference methods(see[1]–[3])and finite element methods(see[4]–[5]).The accuracy of finite element methods is higher than that of finite difference methods. However,the finite difference method is easily implemented,and its computational complexity is much less than that of the finite element method.Moreover,by optimizing the parameters in the finite difference formulas,we can minimize the numerical dispersion and improve the accuracy of the schemes(see[6]).In this paper,we consider the finite difference method for solving the Helmholtz equation with constant wavenumbers.
This paper is organized as follows.In Section 2,we construct a 3-point finite difference scheme for the 1D Helmholtz equation with constant wavenumbers.A convergence analysis is presented to show that the scheme is sixth-order in accuracy.To choose optimal weight parameters of the scheme,a refined choice strategy is also proposed.Numerical experiments are given to demonstrate the efficiency and accuracy of the scheme in Section 3.We show that the proposed scheme not only improves the accuracy but also reduces the numerical dispersion significantly.Finally,Section 4 contains the conclusions of this paper.
2 An Optimal Sixth-order Finite Difference Scheme for the Helmholtz Equation with Constant Wavenumbers
In this section,we propose a 3-point finite difference scheme for the 1D Helmholtz equation with constant wavenumbers. A convergence analysis is then provided to show that the scheme is sixth-order in accuracy.We also present a refined optimization rule for choosing the scheme’s weight parameters based on minimizing the numerical dispersion.
2.1 A Sixth-order Finite Difference Scheme
We next present a 3-point finite difference method for the Helmholtz equation,and then prove that the proposed scheme is sixth-order in accuracy.
We begin with introducing some useful notations. To describe the finite difference scheme,we consider the network of grid points xm,where xm:=x0+(m −1)h.Note that the same step size h:=∆x is used for the variable x.For each m,we set um:=u|x=xmand km:=k|x=xm. Let Dxxu denote the second-order centered-difference approximation for uxx.We begin with establishing a sixth-order approximation for the term uxx.By the Taylor expansion,we have
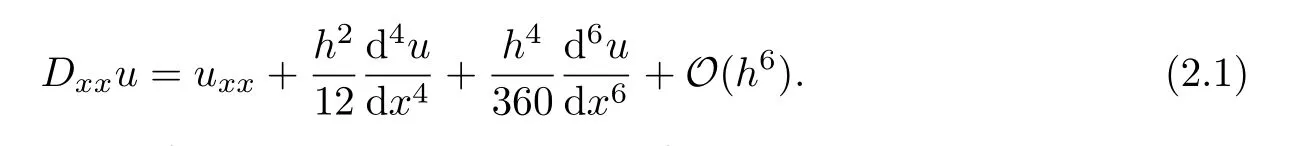
To achieve an approximation of sixth-order with 3 points for uxx,we need to construct an approximation of fourth-order for,and an approximation of second-order forin the above equation.Moreover,both of the approximations should use only 3 points.
Proposition 2.1If the solution u of the Helmholtz equation(1.1)is sufficiently smooth,then there holds
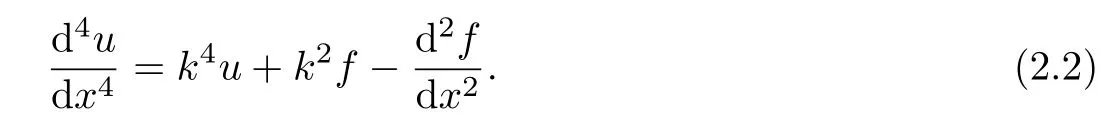
Proof. We differentiate the Helmholtz equation(1.1)twice with respect to x and get that

Combining(2.3)with(1.1)leads to the desired result.This completes the proof.
In the following proposition,we next give another presentation for
Proposition 2.2If the solution u of the Helmholtz equation(1.1)is sufficiently smooth,then there holds
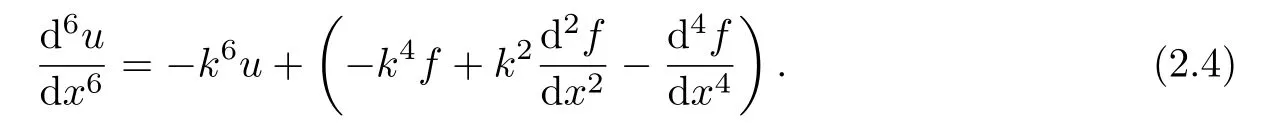
Proof. Differentiating equation(2.3)twice with respect to x yields that
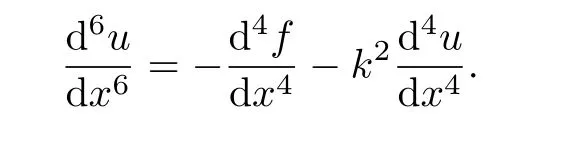
Substituting equation(2.2)into the above equation comes to the conclusion of this proposition.This completes the proof.
Combining(2.1),(2.2)with(2.4)yields a sixth-order approximation for uxxas
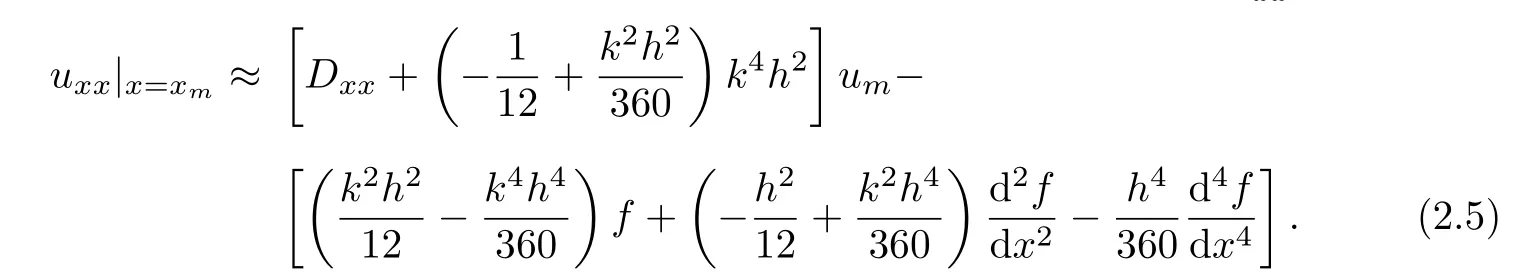
We next establish a sixth-order approximation for the term of zero order k2u.Following[6],we approximate k2u by a weighted-average for the values at 3 points.For this purpose,we set
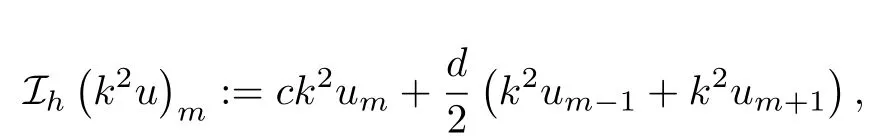
where c and d are parameters satisfying c+d=1.We then introduce an approximation as k2u|x=xm≈Ih(k2u)m.
Based on Ih(k2u)m,we next present an approximation of sixth-order for k2u in the following proposition.
Proposition 2.3If the solution u of the Helmholtz equation(1.1)is smooth enough,then the following equation holds Proof. We first analyze the truncation error for Ih(k2u).By the Taylor expansion,there holds
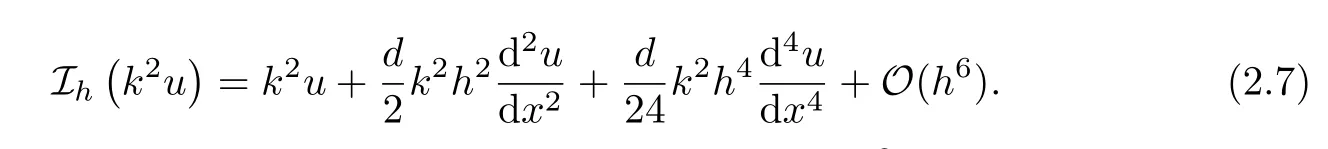
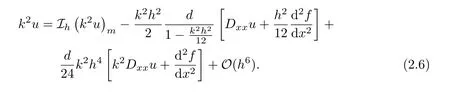
From equation(2.7),to obtain a sixth-order approximation for k2u,we need to construct a fourth-order formula for,and a second-order scheme forFrom equation(2.1),we have
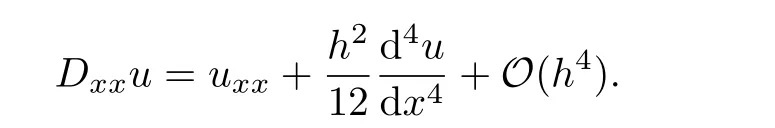
Substituting(2.3)into the above equation,we obtain a fourth-order approximation foras
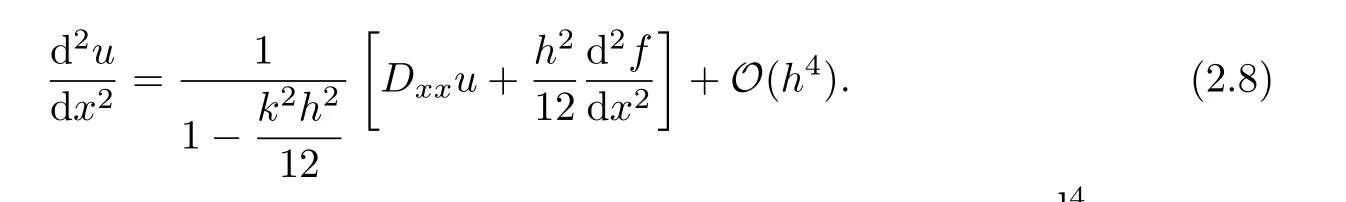
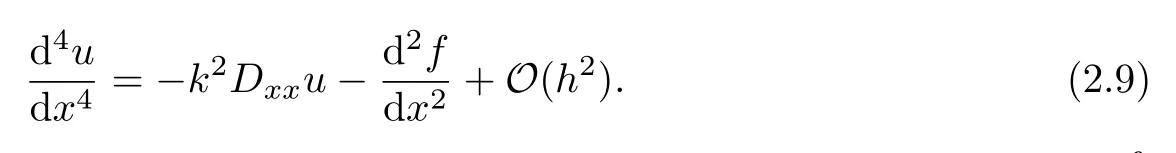
Based on(2.3),we next formulate a second-order approximation for the termas Combining(2.7)–(2.9),we come to the result of this proposition.This completes the proof.
Finally,combining(2.5)with(2.6)leads to a 3-point finite difference scheme for the 1D Helmholtz equation(1.1):
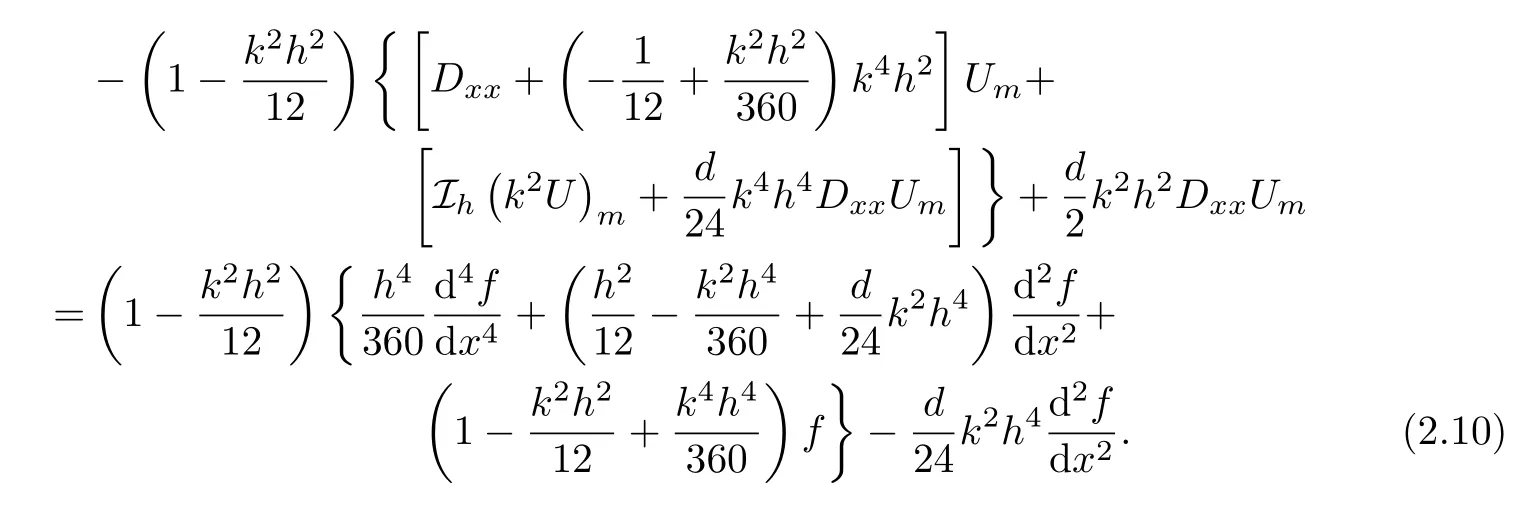
To suppress the numerical dispersion,we follow[2]to introduce a free parameter γ to get a generalization of scheme(2.10):
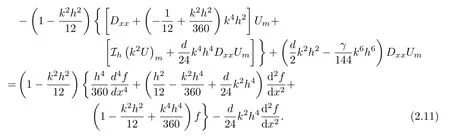
We now turn to considering the convergence of the solution U of(2.11).We shall show that the 3-point finite difference scheme is of sixth order.For ease of notations,we consider a domain I:=(0,1).Let N be a positive integer.Set h:=and ZN:={1,2,,N −1}.For a vector V=[Vm:m ∈ZN],we let
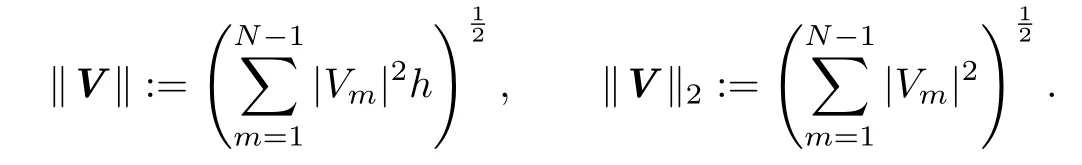
We state the convergence analysis for(2.11)in the following theorem.We only give the proof for the Dirichlet boundary condition and that for the Neumann boundary condition can be obtained similarly.
Theorem 2.1Suppose that the Helmholtz problem considered has a unique solution.If kh is sufficiently small,then there exists a unique solution U for the 3-point scheme(2.11).Moreover,if the solution u of the Helmholtz equation(1.1)with Dirichlet or Neumann boundary condition is sufficiently smooth,then there holds
∥u −U∥≤Ch6,where C is a constant dependent of k,u,f,d and.
Proof. We prove the desired conclusion by analyzing the error equation associated with U and u.We first present the error equation.For each mZN,we let Em:=Umumand introduce
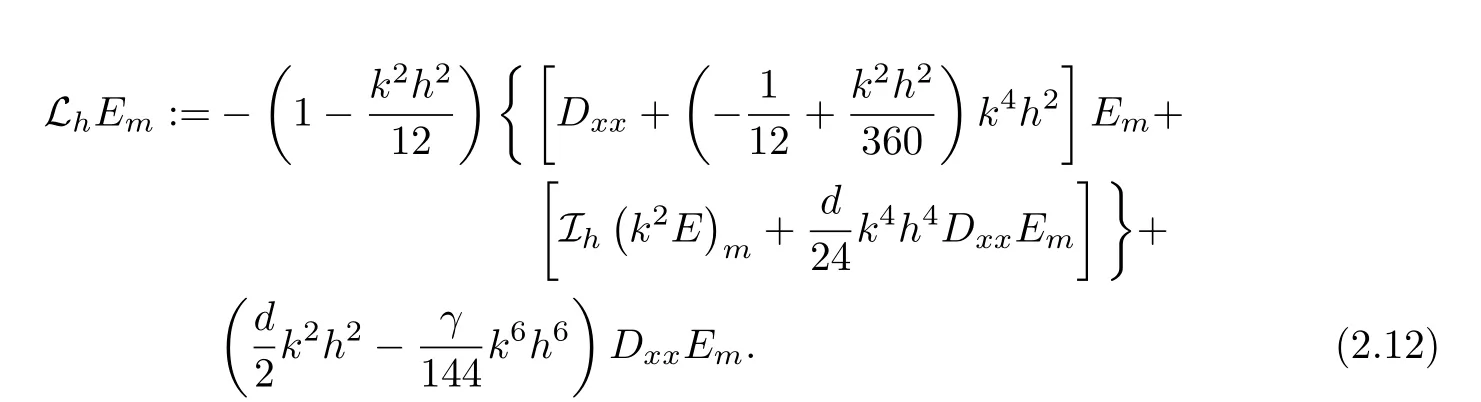
By(1.1),(2.11)and the Taylor expansions for u and f,we have that the error Emsatisfies LhEm=−Rm, m ∈ZN, (2.13)
where Rm:=R|x=xmwith R being the truncation error of the 3-point scheme(2.11)R:=O(h6). (2.14)
Before analyzing the error equation(2.13),we first introduce a matrixD∈R(N−1)×(N−1)as

It is known that the matrix is positive definite.Moreover,the eigenvalues ofDare determined as
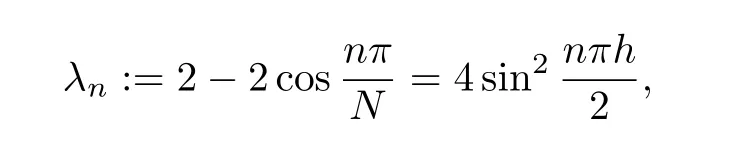
and the corresponding eigenvectors have the form rn:=[rm,n:m ∈ZN]T,with
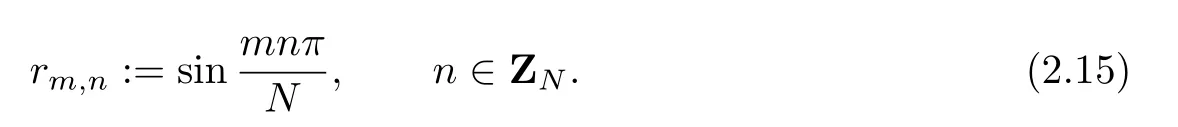
We then rewrite(2.13)as−

whereE=[Em:m ∈ZN]T,R=[Rm:m ∈ZN]Tand

in which Ao,Asare defined as
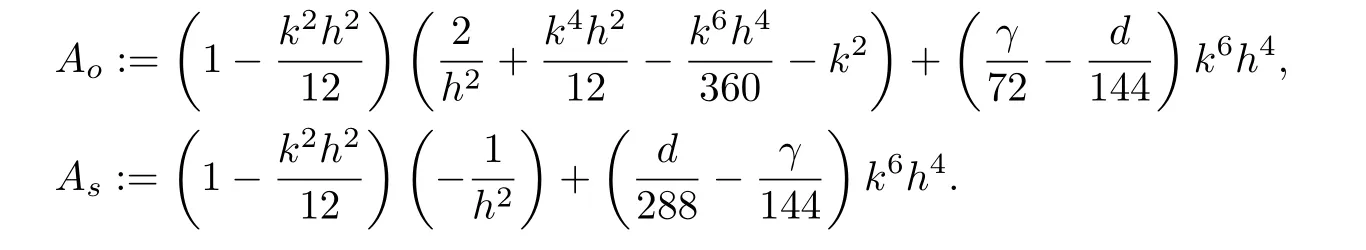
When kh tends to 0,the matrixtends to the matrix D.The matrix D is positive definite,which implies that the 1D problem(2.16)has a unique solution under the condition that kh is sufficiently small.
To estimate the error ∥E∥,we expand E with respect to{rj,j ∈ZN}to get
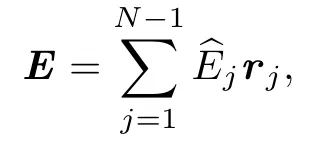
we have
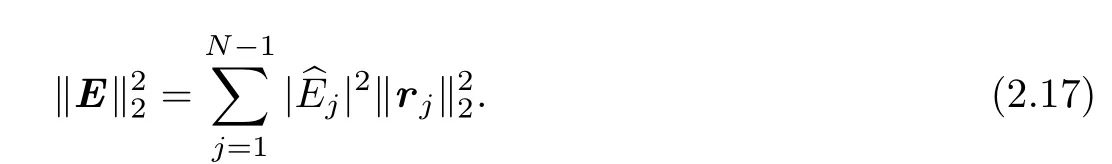
Taking the inner product withE,we derive from(2.16)that

When kh tends to 0,applying(2.17)and the Cauchy inequality,we have for the left hand side term of(2.18)
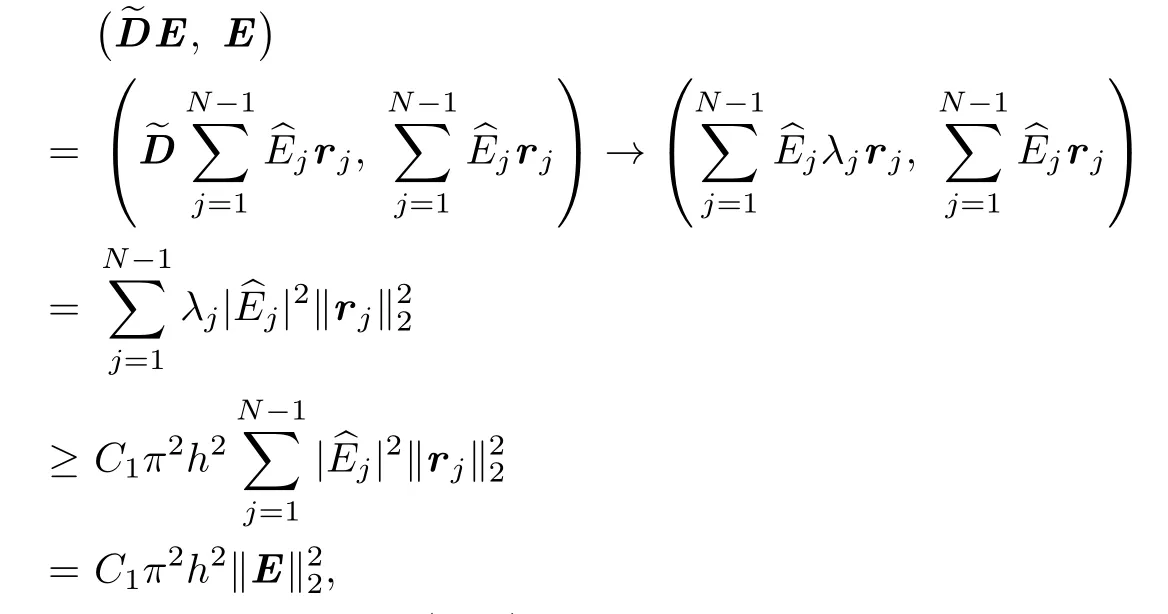
and for the right hand side term of(2.18)
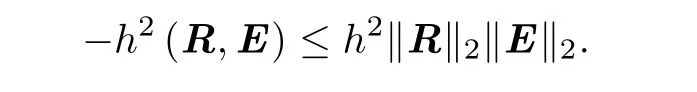
Taking the above two inequalities into(2.18)and using(2.14),it yields
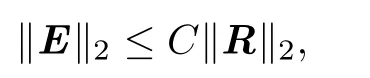
which proves the desired estimate of this theorem.
2.2 Choice Strategies for Optimal Parameters of the 3-point Finite Difference Scheme
In this subsection,a refined strategy is presented to choose optimal parameters for the 3-point finite difference scheme(2.11),based on minimizing the numerical dispersion. An optimization problem is solved with a finer setting to estimate the weight coefficients d and.
We begin with presenting the dispersion equation for the 3-point scheme(2.11). The 3-point scheme(2.11)can be written as
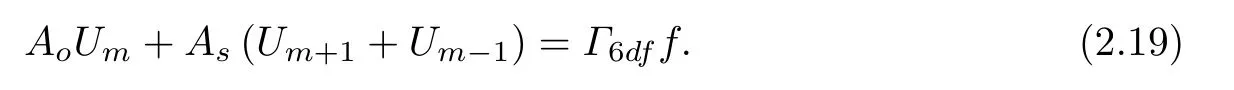
Seen from(2.19),we know that the size of the stencil for the proposed scheme is 3.Following the classical harmonic approach,we next insert the discrete expression of a wave Um:=eikxminto the finite difference equation(2.19). By a simple computation,we get the dispersion equation where P:=cos(kh).

To obtain optimal parameters for scheme(2.11),we consider the numerical dispersion equation(2.20)once more.We first recall some useful notations for wave equations.Let v denote the velocity of wave propagation,λ be the wavelength,and G:=be the number of gridpoints per wavelength. It follows from λ=and k=that kh=. We then multiply h2to both sides of the dispersion equation(2.20),and replace all kh in this equation byt
o obtain
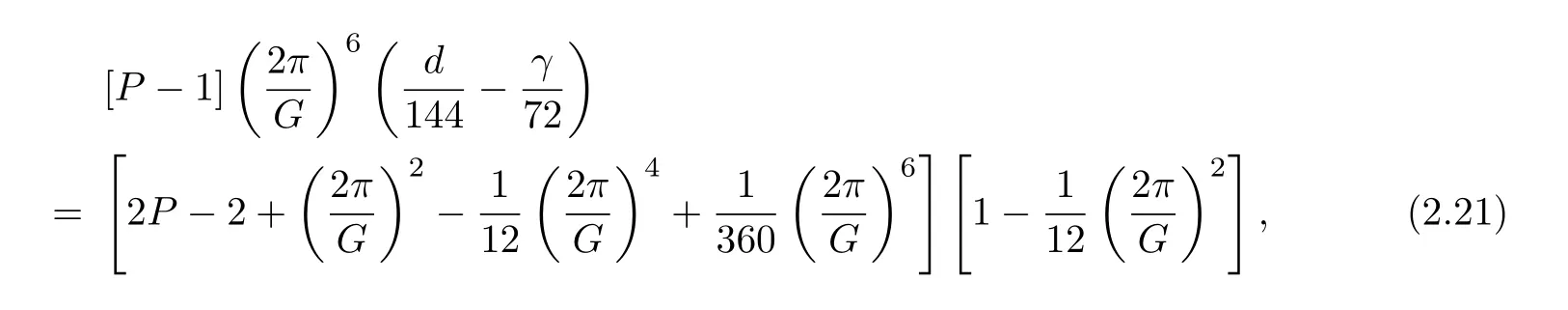
Rule(Refined choice strategy)
Step 1.Estimate the interval IG:=[Gmin,Gmax],and let
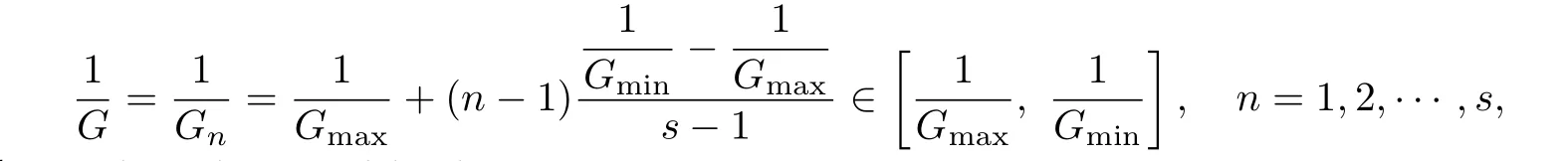
where s is a given positive integer.
Step 3. Applying the least square method method to solve the corresponding system yields the optimal weight parameters for the 3-point finite difference scheme(2.11).
In Table 2.1,we present some groups of refined optimal parameters for the 3-point finite difference scheme(2.11). From now on,we call the 3-point scheme(2.11)with optimal parameters obtained by the refined choice strategy the optimal 3p of sixth-order for short.

Table 2.1 Refined optimal parameters
3 Numerical Experiments
In this section,we present numerical experiments which include the Helmholtz problem with constant wavenumbers to illustrate the efficiency of the schemes proposed in this paper.All the experiments are performed with Matlab 7v on an Intel Xeon(4-core)with 3.60GHz and 16Gb RAM.
In the numerical results reported in this section,the error between the numerical solution and the exact solution is measured in the relative discrete C-norm.In detail,the discrete C-norm is defined as:for any complex vector
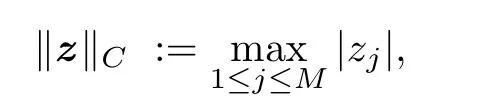
where |zj|is the complex modulus of zj.Let≤ u ≤and uhdenote the exact solution and the numerical solution,respectively.Then,the relative discrete C-norm is defined asIn addition,for the optimal 3-point,the parameters in Table 2.1 are used as refined optimal parameters.
Consider the Helmholtz equation
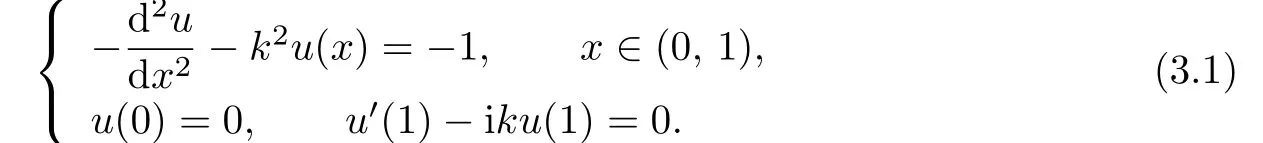
The exact solution of the above problem is
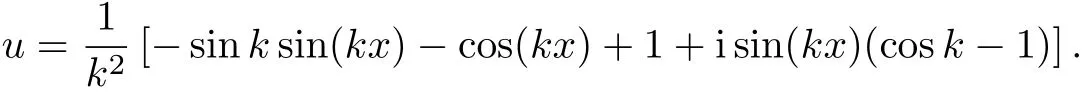
We use this problem to measure the accuracy for two schemes,including the optimal 3-point and the scheme(2.11)with d=γ=0.For this purpose,we next construct a sixth-order approximation for the Neumann boundary condition.Based on the Helmholtz equation and the Neumann boundary condition of the problem(3.1),applying the Taylor expansion yields a sixth approximation for the Neumann boundary condition as
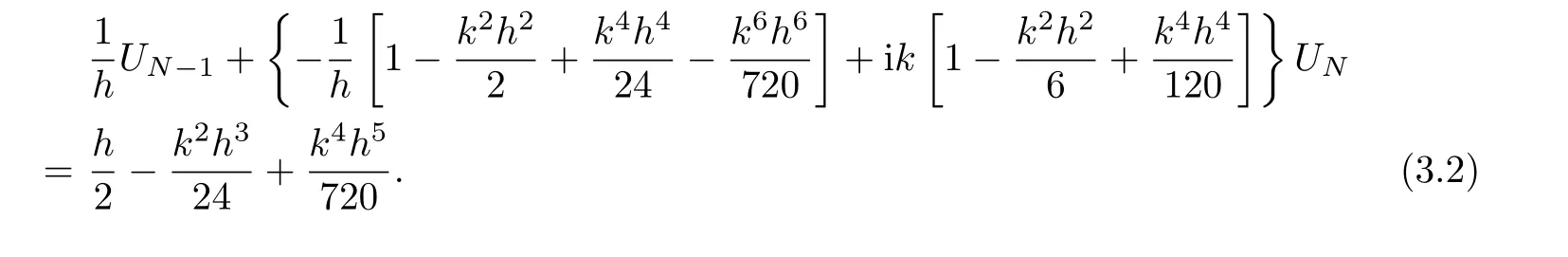
Tables 3.1 and 3.2 show the error in the relative discrete C-norm for two different schemes with different gridpoints N for k=30,200,respectively.We find that,for both the optimal 3-point and the scheme(2.11)with d=γ=0,the rate of convergence for the error in the relative discrete C-norm is of order 6 as expected.In addition,we see that the error for the optimal 3-point is less than that for the scheme(2.11)with d=γ=0,which demonstrates the efficiency of our proposed method.

Table 3.1 The error in the relative discrete C-norm for problem(3.1)with k=30

Table 3.2 The error in the relative discrete C-norm for problem(3.1)with k=200
4 Conclusions
In this paper,we proposed an optimal 3-point finite difference scheme for solving the 1D Helmholtz equation. Firstly,we presented a 3-point finite difference scheme for the 1D Helmholtz equation with constant wavenumbers,and then we provide a convergence analysis to show that the scheme is sixth-order in accuracy. For this 3-point scheme,a refined choice strategy based on minimizing the numerical dispersion was proposed for choosing weight parameters.Finally,numerical examples were given to confirm the the efficiency and accuracy of the optimal 3-point finite difference scheme.
杂志排行
Communications in Mathematical Research的其它文章
- A Nearly Analytic Discrete Method for One-dimensional Unsteady Convection-dominated Diffusion Equations
- Multiple Positive Solutions to Singular Fractional Differential System with Riemann-Stieltjes Integral Boundary Condition
- Planar Cubic G1 Hermite Interpolant with Minimal Quadratic Oscillation in Average
- An SIRS Epidemic Model with Pulse Vaccination,Birth Pulse and Logistic Death Rate
- The Transfer Ideal under the Action of a Nonmetacyclic Group in the Modular Case
- Fekete-SzegInequality for a Subclass of Bi-univalent Functions Associated with Hohlov Operator and Quasi-subordination
