轴承径向游隙对刚性转子不平衡响应的影响研究

金路，苗旭升，王晓锋，黄道琼，李惠敏

(西安航天动力研究所，西安 710100)

某液体火箭发动机涡轮泵转子为拟刚性转子，工作在临界转速以下，研制过程中一直出现振动大的问题。轴承径向游隙是涡轮泵转子-支承系统中的关键工艺参数，是影响转子动力学特性的关键因素。轴承试验和理论研究表明[1-3]，当内圈或外圈为间隙配合时，转子系统表现出较强的非线性振动，且振动幅值大于过盈配合。增加预紧装置可以减小轴承径向游隙，从而降低转子的振动。适当控制轴承径向游隙可以抑制其转子的不平衡响应[4]。

现考虑轴承径向游隙，建立Jeffcott转子模型，分析轴承径向游隙对刚性转子不平衡响应的影响，并进行加装轴承预紧装置的转子动力学试验，对理论推导进行验证。

1 不考虑阻尼时轴承径向游隙对不平衡响应的影响

考虑轴承径向游隙的Jeffcott转子模型如图1所示。图中：Gr为轴承径向游隙；a0为转子中心挠度；O为转子质心；e为偏心距；S为转子几何中心。虽然Jeffcott转子模型对于实际转子来说过于简化，但是通过该模型能够得到转子动力学中重要物理现象的定性分析[5]。

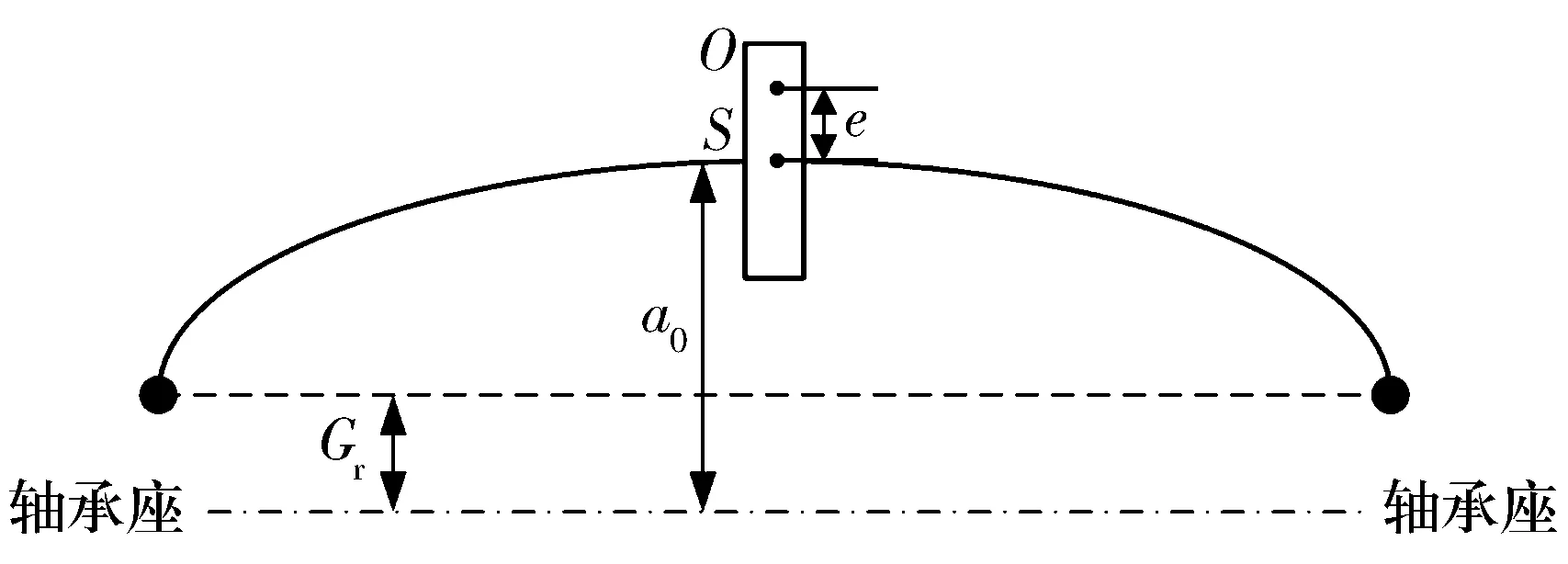
图1 考虑轴承径向游隙的Jeffcott转子模型Fig.1 Jeffcott rotor model considering bearing radial clearance

转子坐标系如图2所示。图中：ω为转子角速度；φ为转子旋转角度。

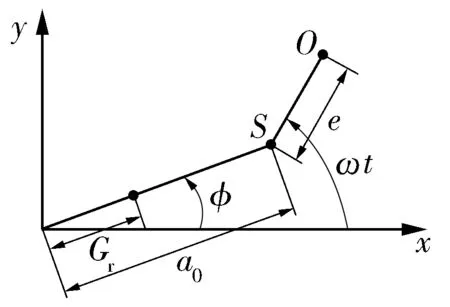
图2 转子坐标系Fig.2 Coordinate system of rotor

建模中考虑轴承分段线性刚度，如图3所示。图中：Fr为径向力；x为径向位移；k′，k分别为轴承游隙范围内、外的径向刚度。

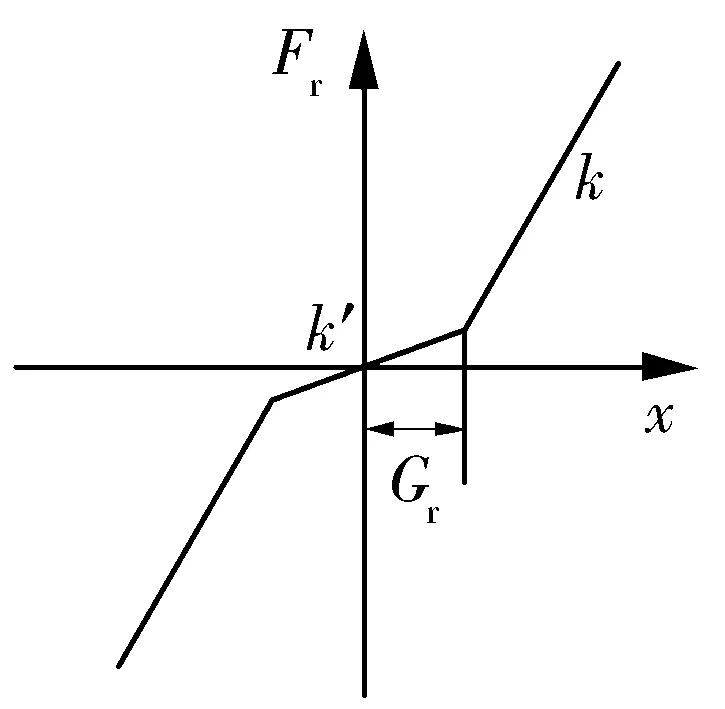
图3 轴承分段线性刚度Fig.3 Piecewise linear bearing stiffness

转子的质心坐标为

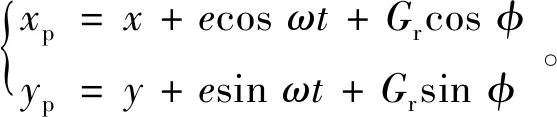
(1)

根据Newton定律可列出平动微分方程

(2)

(2)式忽略了阻尼。将(1)式代入(2)式整理后可得

(3)

引入

(4)

可得

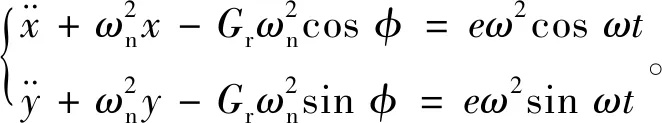
(5)

设定方程(5)的解的形式为

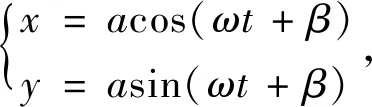
(6)

设定轴承径向游隙的相位为振动的高点，即

φ=ωt+β，

(7)

将(6)，(7)式代入(5)式整理可得

(8)

令

(9)

式中：A为量纲一的振幅；b为量纲一的轴承径向游隙；v为量纲一的转速，为转子角速度与临界角速度的比值。则(8)式可化简为

(10)

转子挠度在轴承游隙范围内时，(2)式变为

(11)

进行类似的推导，并设定

(12)

则该条件下有

(13)

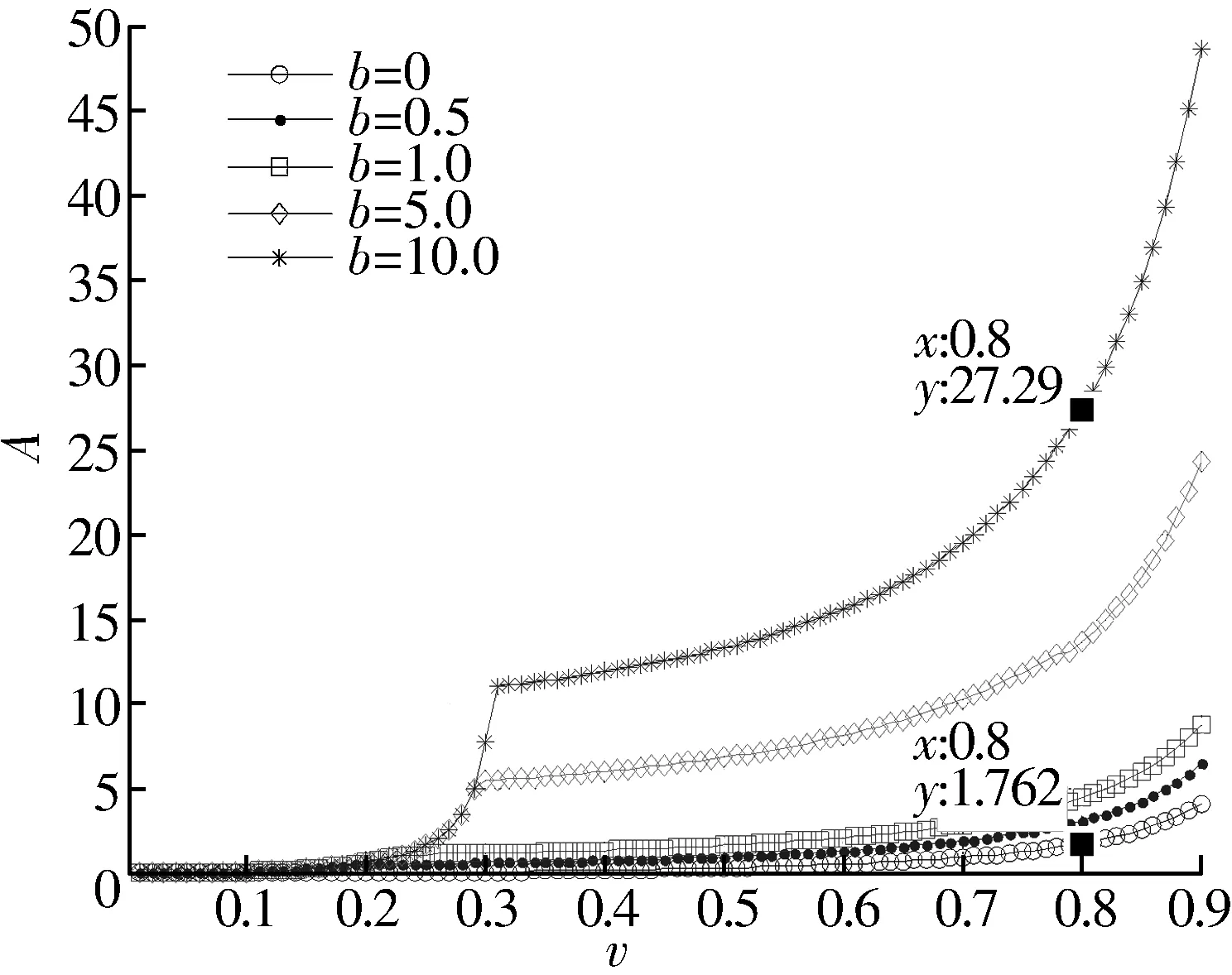
式中：A′为转子挠度在轴承游隙范围内时量纲一的振幅；f为2种分段刚度的比值。当A′

令f=10，转子-支承模型在不同轴承径向游隙下量纲一的振幅随转速的变化曲线如图4所示。从图中可以看出，不考虑阻尼的情况下，随着轴承径向游隙增大，临界转速以下(v<1)的振动幅值增大；在80%临界转速(v=0.8)处，10倍偏心距的径向游隙产生的振动是无轴承径向游隙时的16.6倍。

图4 转子系统量纲一的振幅随转速的变化关系Fig.4 Changes in relationship between dimension less amplitude of rotor system with rotational speed

2 考虑阻尼时轴承径向游隙对不平衡响应的影响

考虑阻尼c时，(2)式和(3)式变为

(14)

(15)

引入阻尼比

(16)

将(4)，(16)式代入(15)式，得到

(17)

将(6)，(7)式代入(17)式整理可得

(18)

进一步整理可得

(19)

将(9)式代入(19)式可得

[(1-v2)2+4ξ2v2]A2-2(1-v2)bA+b2-

v4=0，

(20)

其解为

(21)

当转子挠度在轴承游隙范围内时，将(21)式代入(12)式可得

(22)

当A′

令f=10，ξ=3%，转子-支承模型在不同径向游隙下振幅随转速的变化曲线如图5所示。从图中可以看出，在阻尼比为3%下，随着轴承径向游隙增大，临界转速以下的振动幅值增大；在80%临界转速处，10倍偏心距的轴承径向游隙产生的振动是无径向游隙时的15.5倍。

图5 考虑阻尼时转子系统量纲一的振幅随转速的变化关系Fig.5 Changes in relationship between dimensionless amplitude of rotor system with rotational speed considering damping

3 试验研究

在φ125 mm×φ70 mm×24 mm的轴承外圈加装预紧装置，其可以在工作中将外圈推到一边，从而达到降低轴承径向活动范围的作用，等效于降低轴承游隙。对可加装轴承预紧装置的转子进行动力学试验，试验设备的结构简图如图6所示。用电动机在盘2后端驱动转子，使用位移传感器测量转子的振动位移，测点位置如图中①～⑤所示。共进行2组试验，第1组加装轴承预紧装置，第2组不加装轴承预紧装置。

图6 试验器结构简图Fig.6 Structure diagram of tester

加装和不加装轴承预紧装置转子系统各点的径向跳动量对比见表1。加装轴承预紧装置时，施加2 000 N轴向预紧力。由表1可知，加装轴承预紧装置后，轴系各测点的径向跳动量均有所减小，从而减小转子的不平衡量。

表1 系统测点的径向跳动量Tab.1 Radial runout of system measuring point mm

加装和不加装轴承预紧装置下的振动Bode图如图7所示。由图可知，加装轴承预紧装置并施加2 000 N的轴向力后，在8 000 r/min以下时，转子系统的振动位移明显降低，1倍频峰值由374 μm降为222 μm，降幅高达40.6%；转速在8 000 r/min以上时，减振效果不明显，说明该轴向力偏小，不足以影响转子振动。

图7 转子系统振动Bode图Fig.7 Bode diagram of vibration of rotor system

4 结论

在亚临界转速下，加装轴承预紧装置，适当减小轴承径向游隙可有效降低转子-支承系统的振动。试验表明，施加2 000 N轴向预紧力时，转速8 000 r/min以下的转子振动幅值明显降低，验证了理论推导的正确性；转速8 000 r/min以上的转子振动幅值无明显变化，轴向预紧力、转速与轴承预紧装置对振动抑制的影响有待进一步研究。