基于改进孤立点算法的异常交通数据识别

2019-07-23李硕张萌萌陈勇恒

山东交通学院学报 2019年2期

李硕，张萌萌，陈勇恒

(山东交通学院交通与物流工程学院，山东济南 250357)

0 引言

在交通数据集中，有很多明显异常的数据，如空数据、乱码数据、负值数据等。目前国内外学者采用不同方法对交通数据质量控制中的异常数据进行识别，通常通过交通参数之间的关系或者过程统计聚类的方式识别异常数据。Polat等[1]结合分类器算法提出一种新的数据预处理方法，即减法聚类属性加权。Deb等[2]利用数据与数据之间的关联估算数值或分类值的缺失数据。Li[3]结合小波包能量分析和主成分分析，实现交通检测器的数据故障识别。吴芳[4]建立基于边界检测算法和孤立点检测算法的异常数据判别模型。陆化普等[5]建立基于数据驱动的动态阈值模型，计算交通流参数的实时阈值，实现交通异常数据的实时识别。谢羲[6]结合交通数据的时间分布特性和空间分布特性，利用小波变换理论对交通数据进行去噪。上述异常数据识别方法虽然比传统阈值筛选法检测率高，但在不同交通情况下，检测率和误检率存在很大波动。本文基于对异常数据的识别，对基于相似系数和的孤立点算法进行改进，并通过实例对分别采用传统阈值筛选法与改进后的基于相似系数和的孤立点算法对异常数据的识别进行对比分析。

1 交通数据采集与异常因素分析

1.1 交通数据采集

交通数据分为静态交通数据和动态交通数据，动态交通数据在复杂的交通状况中难以采集，易受各种交通环境的影响。动态交通数据按交通信息产生的形式分为：1)原始交通信息。由道路上或环境中直接采集到的各类交通状态与交通环境信息。2)加工交通信息。经过处理后的交通信息，如车辆等待时间、区间行程速度、预测行程速度、平均停车次数等[7-14]。

1.2 异常因素分析

数据的发展和建设是交通行业最重要的部分，通过各种检测器以及检测技术最终传送到终端的数据质量会有明显的差异，导致这种差异的常见原因有：1)检测设备发生故障、断电或通信链路发生故障，直接导致数据大批量缺失；2)随着时间的推移，设备变得陈旧，检测精度降低，造成检测数据不准确甚至失去效用；3)设备在检测或传输过程中，受到外界条件的影响，造成设备检测或传输的不稳定，产生部分异常数据；4)数据中心发生意外情况，如不正常关闭系统等，导致数据出现间歇性丢失或异常[15-23]。

2 交通异常数据识别

2.1 传统阈值筛选法

在各种异常数据筛选算法中，较为基本的也是筛选条件较为宽松的是交通流参数的阈值筛选法。传统阈值筛选法根据道路交通状况给交通量或者是地磁检测器的时间占有率规定一个阈值(范围区间)，如果某一数据不在阈值范围内，则这条数据为异常数据。

检测器最大时间占有率的阈值为 90%～99%，一般情况下，在多车道检测记录中，其时间占有率不超过95%，因此，传统阈值筛选法的阈值一般为 95%[24]。定义交通量的合理范围为：

0≤Q≤kCt/60，

式中：C为道路通行能力，辆/h；t为数据采集时间间隔；k为修正系数，一般取k=1.3～1.5。

2.2 孤立点法

孤立点是指数据集中与众不同的数据，这些数据并非随机偏差, 而是产生于完全不同的机制[25]。孤立点检测算法在非交通领域应用很广，在交通领域应用该算法也可以找出波动异常的数据。

2.2.1 传统孤立点检测算法

传统孤立点检测算法的基本思想是计算两两数据之间的距离或密度等能够评判数据波动的指标，主要有4种方法。

1)基于统计的孤立点检测算法。其核心是观察数据集中数据的特征，按照其特征建立数学分布模型，不符合此模型的数据为孤立点数据，这种算法比较适用于单一属性的异常数据检测，实际情况下，大多数数据并不符合理想状态下的数据分布，且大都是多属性的，故此方法在交通数据的孤立点挖掘方面比较困难。

2)基于距离的孤立点检测算法。其核心思想是以相邻数据之间的距离检测小样本数据，距离远即没有邻居的点被判定为孤立点。但基于距离的孤立点检测算法是从数据的整体出发，而交通数据在不同时间段有不同的变化规律，用该方法检测交通数据的异常数据误差较大。

3)基于密度的孤立点检测算法。其核心思想是通过局部异常因子算法确定异常点数量。首先需要定义孤立点检测算法的局部范围，靠近范围中心点的对象的局部异常因子接近1，范围以外的对象的局部异常因子大于1，因此，通过局部异常因子可以判断异常值。但是基于密度的孤立点检测算法中的局部范围很难确定，不同的范围有不同的筛选结果。

4)基于偏离的孤立点检测算法。其基本思想是观察数据集中数据的特征，如果某对象的数据特征不符合应有的或给定的特征描述，则判定为异常数据。此算法对异常数据的判定太过理想化，故很少采用。

2.2.2 基于相似系数和的孤立点检测算法

在交通多属性数据中，传统的孤立点算法只能对数据中的每一个属性分别进行检测，将各个参数之间的关系分割开来，忽略各参数间的内在联系，在交通大数据环境下，大大增加了运算的复杂程度。基于相似系数和的孤立点算法，可以对同一目标多属性的数据集进行相似度检测，能大大减少运算的复杂程度。

以交通地磁数据为例，由于地磁数据含有交通量和时间占有率两个属性，则需要检测的数据用矩阵表示为

X=[X1X2]，

(1)

式中：X1为交通量矩阵，X1=[x11x21…xn1]T；X2为时间占有率矩阵，X2=[x12x22…xn2]T。

将输入数据在[-1，1]上进行归一化处理，检测出孤立点后再将其还原，式(1)归一化处理后的矩阵(按数据检测时间排序)

(2)

为了判断两两数据之间的差异程度，数据的相似度按时间排序并构成相似系数矩阵

(3)

式中：rij为第i行数据与第1、2行数据两两之间的相似系数，i=1，2，…，n，j=1，2。

rij的计算公式为：

(4)

图1 孤立点算法流程图

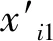
交通量和时间占有率两个属性的相似系数和

(5)

Pi越小，说明某一条数据与其他的数据的距离越远。

第i行数据与第1、2行数据之间的相似度

(6)

式中：Pmax为n个相似系数和中的最大值。

当λi大于经验设定的相似度λ的阈值时，判定第i条数据为孤立点数据。其判定流程如图1所示。

2.2.3 基于相似系数和的孤立点算法的改进

1)基于相似系数和的孤立点算法的不足

b)基于相似系数和的孤立点算法通常采用经验法主观设定异常数据的阈值，不利于异常数据的精确判定。

2)基于相似系数和的孤立点算法的改进

a)相似系数计算方法的改进。依据交通数据的特点，按照不同城市不同交通出行规律，将交通数据划分为夜间、高峰、平峰3个时段，将3个时段的数据按时间进行排序，分别将3个时段内第1行与第2行数据设定为基准值，分别计算各时段内的所有数据与对应时段的基准值之间的相似系数。

b)异常数据阈值设定方法的改进。通过以交通量和时间占有率逐次逼近基础值的方法发现阈值的变化规律，进行阈值设定。任意选取一个时间段进行异常数据阈值设定，流量从0开始逐次逼近，由于交通量与时间占有率之间存在一定的对应关系，考虑到交通量-时间占有率模型以及拟合分析的复杂性，本文仅选取与实验数据具有相同车道功能属性，且在同一时段内的多段历史数据作为参考，人工确定不同交通量下时间占有率的估算值；然后再计算每一次逼近后的数据与基础值之间的相似度，最终通过人工确定较为合适的相似度作为异常数据判定的阈值。表1中的交通量为5 min内通过交叉口断面的车辆数，时间占有率为5 min内通过交叉口断面的车辆压过检测器的时间与总时间的比值。

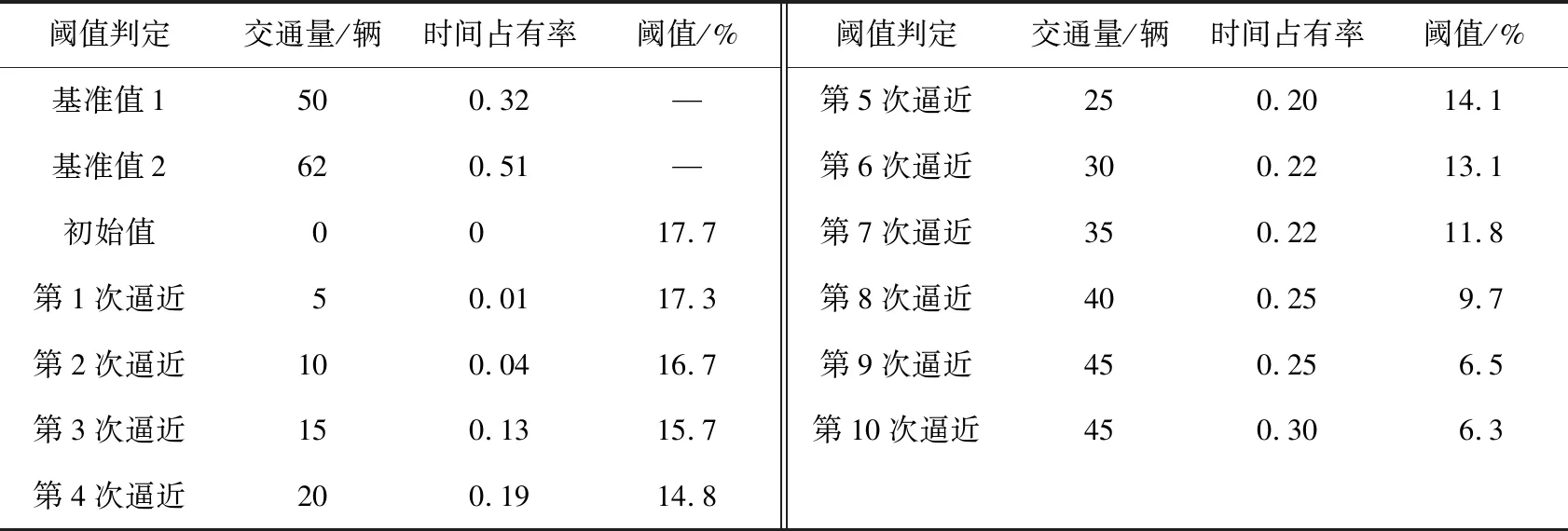
表1 阈值的判定

由表1可以看出，随着流量和时间占有率不断接近基准值，阈值变得越来越小，即在第8～10次的逼近中，设定的交通量和时间占有率与基准值比较接近，而在第8次逼近之前，设定的交通量与时间占有率与基准值相差较大，因此阈值取6.5%～9.7%。

3 试验分析

分别选取济南市经十东路与凤山路交叉口的高峰时段和平峰时段的正常数据作为数据源，人工将部分正确的数据修改成异常数据，分别计算传统阈值筛选法与改进后的基于相似系数和的孤立点算法的检测率(测得的异常数据的数量占实际异常数据数量的比值)和误检率(错检数据的数量与正确数据数量的比值)，将计算结果进行对比。

1)检测率

Dt=dt/s，
Dp=dp/s，

(7)

式中Dt、Dp分别为传统阈值筛选法的检测率与改进后基于相似系数和的孤立点法的检测率，dt、dp分别为传统阈值筛选法与改进后基于相似系数和的孤立点法检测到的异常数据数量，s为实际人工修改成异常数据的数量。

2)误检率

Ft=ft/N-s，
Fd=fp/N-s，

(8)

式中：Ft、Fd分别为传统阈值筛选法和改进后基于相似系数和的孤立点法的误检率,ft、fd分别为传统阈值筛选法与改进后基于相似系数和的孤立点法的误检数,N为试验样本总数。

选取2 d早高峰时段数据为第1次试验的数据源，人工将正确数据修改成的错误数据占总数据的32%，由式(1)得含有交通量和时间占有率2个属性的矩阵

(9)

采用最大-最小归一化方法，由式(2)(9)得到归一化后的矩阵

由式(3)(4)得相似系数矩阵

由式(5)(6)得到相似度矩阵

将计算得到的相似度矩阵λi与通过表1设定的阈值进行比较，当λi大于设定的相似度阈值时，第i条数据被判定为异常数据，进而得到异常数据的数量，通过式(7)计算改进后的基于相似系数和的孤立点算法的检测率；同理，当正确的数据被改进后的基于相似系数和的孤立点算法误检成异常数据时，即此条数据为误检数据，对误检数据的数量进行统计，通过式(8)计算改进后算法的误检率。用传统阈值筛选法与改进后的基于相似系数和的孤立点算法计算的检测率分别为25%和75%；误检率分别为0与5.9%。

同理，选取4 d早高峰时段数据作为第2次试验的数据源，将其20%的数据人工修改成错误数据。用传统阈值筛选法与改进后的基于相似系数和的孤立点法得到的检测率分别为27.3%和72.7%；误检率分别为0与8.5%。

因此，改进后的基于相似系数和的孤立点算法在交通异常数据识别中，检测率基本稳定在70%以上，传统阈值筛选法检测率约为25%，即改进后的基于相似系数和的孤立点算法更适应于交通异常数据的识别，因为传统阈值筛选法的阈值上下限取值比较宽泛，因此无法识别存在于传统阈值设定范围内的异常数据。传统阈值筛选法的误检率在2次试验中都为0%，其根本原因为上下限取值宽泛所致。而改进后的基于相似系数和的孤立点算法在交通异常数据识别中，其误检率基本稳定在10%以下，因此，相对于传统阈值筛选法的异常数据检测，改进后的基于相似系数和的孤立点法更加适用于复杂多变的交通异常数据识别。