面向智能电网网络拓扑结构错误的最快自适应估计算法研究

王康毅

（长治学院，山西 长治 046011）

0 引 言

近年来，智能电网的迅速发展得益于它具有良好的经济效益、环境效益及社会效益[1]。随着现代通信技术的发展，未来电网具有支持双向信息和电力流的能力、有效地解决断电能力及加快可再生能源融入电网的能力[2]。

状态估计在建立电网网络实时模型中起到了重要作用。现代能源管理系统中，需收集两类数据用于状态估计。（1）开关和断路器的状态数据。（2）总线电压、注入功率、功率流及电抗的模拟数据。其中，状态数据用于确定网络的实时拓扑结构，模拟数据用于确定线路和变压器的负载/电压曲线。由于丢失数据、通信错误或是测量误差，状态数据和模拟数据都存在偏差。状态数据中的错误将显示为网络拓扑中的错误，将导致状态估计误差。

能源管理系统必须有效解决网络拓扑结构错误，并及时防止对整个网络的进一步损坏[3]。应尽快确定网络的拓扑结构，以迅速检测或识别错误的数据。状态估计可保持一个可靠的数据库，否则错误的数据可能会导致智能电网的无效运行和网络的整个实时建模过程中拓扑结构发生错误[4]。这种类型的估计问题可通过最快检测（QD）的概念来解决。最快检测是基于在线观察用户定义的决策规则和检测精度发生的变化，尽快改变观察到的统计信息。决策规则需要正确设计，以权衡停止时间和决策准确性。

本文采用了自适应估计算法，以帮助检测和有效识别智能电网中的拓扑结构错误[5]。提出的方案能实现如下功能。（1）可执行所有总线产生的相互干扰的信息流的调解。（2）在不违反规则的前提下，尽快确定当前网络拓扑结构，包括估计的精度。结合当前网络拓扑结构知识，可很快确定拓扑结构错误。此外，本文开发的算法，可提供定量性能分析的理论指导分析模型。该分析模型可为提供配置系统参数进行网上最快估计[6]。依据基本性能指标，可计算出在检测延时框架下的误警率（FAR）和误测率（MDR）。本方案中，基于马尔可夫链的分析模型有两个不同的转变概率矩阵（TPMs）：一个是在正常数据环境下，一个是受恶意数据攻击的环境下。正常的转变概率矩阵可帮助确定初始状态。初始状态下，可通过转变概率矩阵来监测受攻击情况下的误测率。该算法的性能是由两种数学分析和数值模拟评估，如误警率、误测率及平均样本数。

1 系统模型

智能电网的状态估计模型如图1所示。

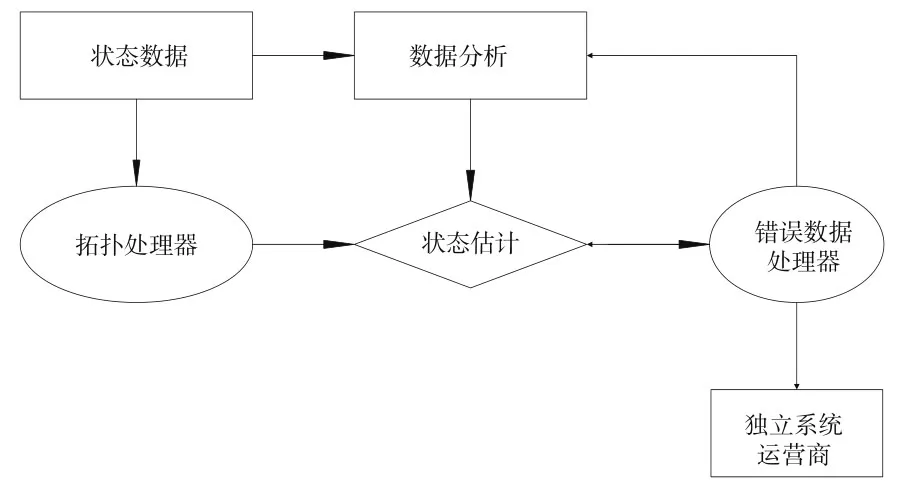
图1 系统模型

由图1可知，网络拓扑处理器模块使用断路器和开关的遥测数据，以确定该系统目前的网络拓扑结构[7]。然后，状态估计模块会处理所有的测量数据（状态数据和模拟数据），并采取冗余性的优势来检测任何错误数据。如果数据存在错误，错误数据处理器将通知状态估计器，然后，电力系统的状态估计将会被丢弃，重新估算一次。如果数据没有出现错误，该独立系统运营商（ISO）将会通过电流来控制发电机和负载，以达到不同的功能，如自动发电控制、最优功率流控制或者能源管理系统控制等。如果发生意外，错误的数据可以放大对智能电网的负面影响。因此，对测量数据的在线错误检测是必不可少的。此外，由于模拟数据中的错误将导致状态估计误差，所以应分析拓扑结构的错误。

1.1 传统的错误数据监测（BBD）

经典表述的状态估计正规方程如下，控制中心观测M的实际功率测量的向量Zn，有关的状态向量x的非线性方程为：

其中，Zn=[Zn,1,…,Zn,M]T，en是零均值和协方差矩阵为Σe的高斯测量噪声。

通过将测量值和状态矢量中的有功和无功部分去耦合化[8]。假设在电网两条总线间的相位差都很小，则式（1）的线性近似是准确的，可得：

其中，Zn是该组的功率测量向量，x是[θ1,θ2,…,θN-1]T的实部，H∈RM是相对于相位角的测量雅克比矩阵，则状态估计为：

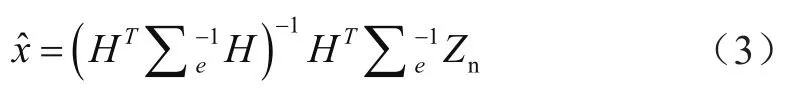
1.2 拓扑结构问题

拓扑误差的影响可呈现在H中，它的初始值为零。系统可执行错误数据监测来确定由一些综合算法导致的错误，如顺序搜索算法，用加权最小二乘状态估计的卡方检验或最大归一化的剩余测试。因此，网络拓扑结构的错误可分析估计为：

其中，H是真雅克比测量值，He是假雅克比测量值，B是雅克比错误矩阵。代入式（2）替代为线性近似模型：

1.3 问题模型

实际上，可把智能电网中的每条总线比做是通过公共通信渠道来收发信息的发送器。将式（2）的范围变大：

其中，en,r是测量噪声。

2 提出的方案

2.1 概 述

第一步，利用式（3）估计，然后在可能的逻辑错误情形中分析雅克比矩阵，如，可确保在后面的精确度。由于测量的M和N数量较多，所以去掉一个测量值不会影响估计。

第二步，考虑Zn在式（6）中的多址格式。根据可以估计。

2.2 数学分析

马尔可夫链为基础的分析模型可产生保证该方案基本性能指标的参数配置，能提供定量性能分析和理论指导。

2.2.1 模型分析

方案中的马尔可夫链转移概率从状态i的(k-1)时刻到j的k时刻，可表述为：

可计算出转移概率矩阵P和，其矩阵是F阶的方阵，F是指马尔可夫链中共有F个状态，从任意一个状态出发，经过任意一次转移，必然出现1，2，3，…，F中的一个状态。

马尔科夫链的过程中，正常状态开始的初始稳态概率，可被确定为：

其中，j=1，2，3，…k。最终的稳态概率可被确定为：

其中，i=1，2，3，…k；j=1，2，3，…k；转移概率矩阵中，每一行转移概率之和等于1，即

2.2.2 误警率的期望值

误警率（FAR）的期望值可确定为：

2.2.3 漏检率的期望值

漏检率（MDP）的期望值可确定为：

其中，C是延迟常亮。

3 性能分析

同时使用数学分析和数值模拟，通过MATPOWER4.0软件的模拟测试验证该方案。

图2为总线i的解码/估计Hr,i的说明性示例。仿真结果表明，该阈值A是0.017，阈值B为92。

由图2可知，最小停止时间T（值为12）曲线在阈值A处坠落，并且此情况下的值是-1。

图3显示了平均样本数（ASN）对系统参数c0和c1的影响。x轴是总线标号，y轴为每个总线对应的ASN。图3中有3个参数设置：最低成本c0=1，c1=2；平均成本c0=3，c1=4；最高成本c0=6，c1=8。

图2 IEEE-14节点测试系统下的模拟快速检测方案下的确定总线i的Hr,i的值（虚线表示阈值A，实线表示阈值B）

图3 IEEE-14节点测试系统下的三组错误情况下的ASN

由图3可知，成本较高的错误拒绝假设会导致更大的ASN（即系统需要花费更多的意见做出决定）。

图4和图5中显示了在相同设置和相同输入数据情况下，误警率的期望（E[FAR]）和漏检率的期望（E[MDR]）。通过从MATPOWER4.0中获得的电力流数据值，可进行性能值（E[FAR]，E[MDR]）的分析和模拟结果的比较。

图6为改变ASN的计算循环次数下的计算复杂度比较。

由图6可知，虽然这两种算法的性能随着线性周期的数目增加而增加，但是本文提出的方案的计算时间比传统算法的计算时间要短70%。

4 结 论

本文主要是以最小延迟，帮助检测和有效识别智能电网网络的拓扑错误为目的进行在线估计网络拓扑。自适应最快估计算法，在不违反给定的限制条件下，成功确定了当前网络拓扑，使操作人员可快速确定并及时识别网络拓扑错误。此外，制定了基于马尔可夫链的分析模型，以定量研究系统参数。低成本的情况下，该方案可保证误警率和漏检率的确定，且该方案比传统方案更有效率。Power Engineering Review，1980，1（1）：19.

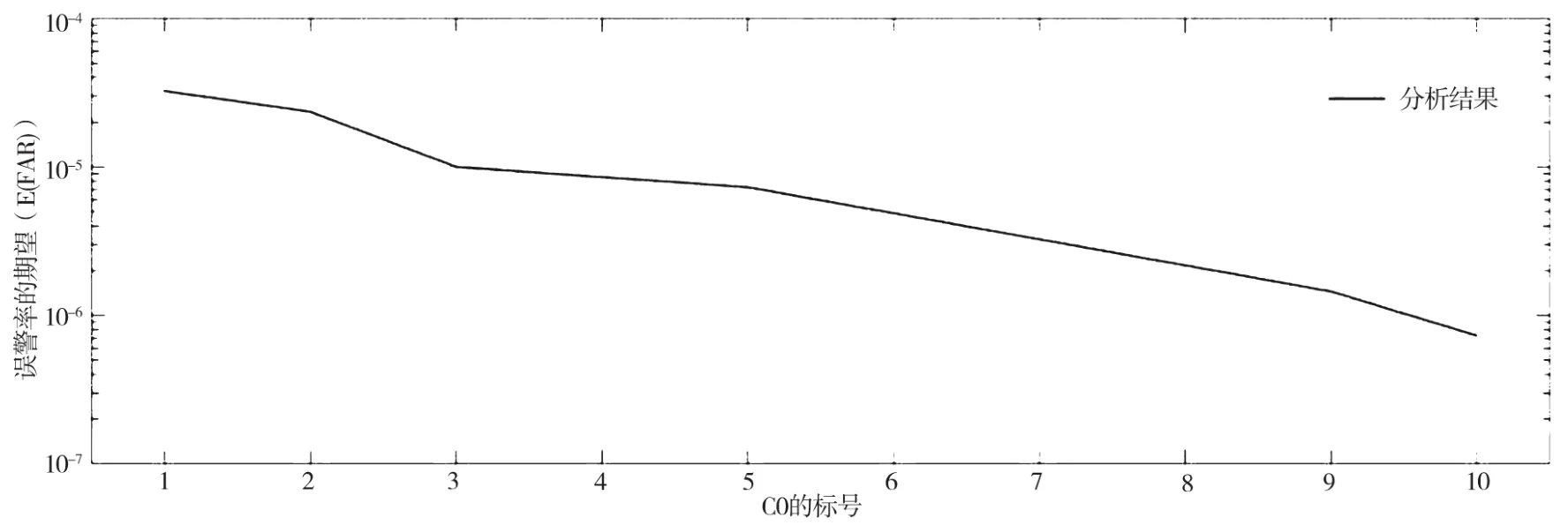
图4 误警率的期望（E[FAR]）

图5 漏检率的期望（E[MDR]）

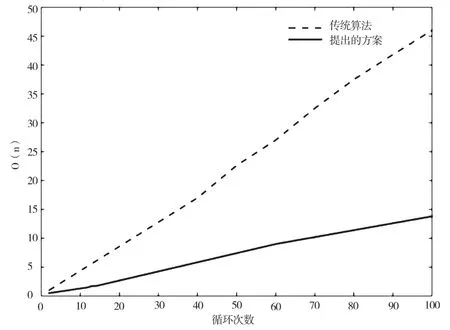
图6 改变ASN的计算循环次数下的计算复杂度比较