“二八灰土”回填地下粮仓浮力预警试验研究

刘海燕，孟伟新，王振清，田栋杰，徐向楠，刘 旭



“二八灰土”回填地下粮仓浮力预警试验研究

刘海燕1，孟伟新1，王振清1，田栋杰2，徐向楠1，刘 旭1

（1. 河南工业大学土木建筑学院，郑州 450001； 2. 郑州康桥房地产开发有限责任公司，郑州 450000）

地下结构的浮力多以阿基米德定律为基础进行计算，未考虑周围回填土体。该文以某地下粮仓为研究对象，考虑周围回填二八灰土的实际工况，分别进行直径为400（模型筒A）、500（模型筒B）、600 mm（模型筒C）的室内缩尺模型试验。试验包含纯水试验和回填二八灰土试验。纯水试验结果表明，以阿基米德定律计算的实际浮力与模型筒自重（包含模型筒上部约束反力所折算自重）的理论浮力基本一致，模型筒A、B、C的实际浮力与理论浮力的误差分别为0.03%、1%、3%。在回填二八灰土试验中，通过缓慢注水，利用位移计、压力传感器监测模型筒位移及模型筒上部的约束反力，分析了模型筒整个上浮过程中位移和约束反力的变化情况。位移突变值滞后于约束反力突变值，压力传感器读数发生明显变化而位移计读数未发生明显变化所测量的水位为警戒水位，压力传感器与位移计读数均发生明显变化所测量的水位为实际起浮水位。以警戒水位和实际起浮水位作为理论计算依据，得出警戒水位和实际起浮水位时模型筒自重（包含模型筒上部约束反力所折算自重）作用下理论抵抗浮力及计算所得的实际抵抗浮力。警戒水位时模型筒A、B、C实际抵抗浮力为理论抵抗浮力的1.93、2.43、1.66倍。实际起浮水位时模型筒A、B、C实际抵抗浮力为理论抵抗浮力的2.15、3.36、2.96倍。从安全储备方面综合考虑，回填工况地下粮仓在预警水位时实际抵抗浮力为理论抵抗浮力的1.5倍，实际起浮水位时抵抗浮力为理论抵抗浮力的2倍，研究结果为今后地下粮仓及其他地下结构的抗浮设计提供参考。

浮力；水位；试验；二八灰土；回填工况；地下粮仓；注水试验

0 引 言

中国各地粮仓中粮食储藏总量达2亿吨，保障粮食安全是农业现代化的重要任务[1]。粮食仓储设施是保障粮食安全、关系国计民生的重要基础设施[2]。但目前中国在建的粮仓仍以高大平房仓，大直径浅圆仓为主，占用大量的土地资源，储粮环境并不理想[3]。利用地下仓储粮，是一种利用天然地下自然低温、低湿和密闭缺氧环境，达到抑制虫霉危害、延缓粮食陈化目的，实现绿色、低温和生态储粮的好方法[4]。且中国地下贮粮有着悠久的历史，远在五六千年前中国原始社会的仰韶文化时期，人们就用口小底大的袋状窖穴贮粮[5]。隋朝时期隋炀帝杨广在洛阳兴建了含嘉仓、兴洛仓、回洛仓。20世纪70年代国家建造了窑洞仓、喇叭仓、管形仓等一批地下仓型，以地下土圆仓（喇叭仓）仓型为最好[6]。为了适应新形式下粮食储存的需求，更好的发挥地下粮仓恒温、节能、节地、绿色、环保的优点[7-8]目前中国建造了新型的地下钢筋混凝土散装粮食圆形筒仓。

伴随新型地下粮仓向高水位等复杂地质条件地区的推广，仓体将受到较大的地下水的作用[9]。对于地下结构浮力问题一直争议至今，目前地下结构浮力计算多以经典的阿基米德定律为基础，忽略土体对结构抵抗浮力的有利因素。对此，诸多学者进行了讨论：李广信等[10-11]认为地下结构浮力的实质是有效应力原理在弱透水层中的适用性，并提出凡是地下水位以下的结构物均按其排除的体积计算浮力是不合适的；方玉树[12]针对这个问题提出了水压率的概念,在此基础上修正了孔隙水压力、浮力、浮重度、渗透力、固结系数和贮水率的计算方法；饶清等[13-14]根据不同地区地下水的埋藏条件对抗浮设计水位取值与浮力折减现象进行了分析；也有国外学者[15-18]从微观土颗粒与水相互作用的角度开展研究；王洪新[19]从水土压力的角度提出一个新的可以应用于地下结构水土压力分算与合算统一算法的强度理论；白晓宇等[20]对地下支护结构的抗浮锚杆进行了原位试验研究；也有学者们从地下水的渗流[21]，地下土体中孔隙水压力与浮力的关系[22]，浮力的实质[23]等方面展开研究；除上述理论研究外，另有一些学者设计了一系列的抗浮模型试验：如唐春华等[24]通过模型试验的方法对砂土地基中地下水浮力的力学效应进行分析，得出砂土地基中地下结构所受浮力按静水压力计算是合理的；而梅国雄等[25-27]对黏土地基开展浮力模型试验，得出黏土地基中浮力由于土体的吸附作用存在少量的折减；周明[28]、张第轩[29]则对不同的土层进行浮力模型试验，由于试验思路的不同，导致试验的结果离散性较大。

该文以周围回填二八灰土的地下粮仓为模型，进行了直径为400、500、600 mm的模型筒试验，测试并分析模型筒位移及约束反力变化情况，研究分析模型筒在回填工况下的浮力变化以及模型筒实际抵抗浮力大小与理论抵抗浮力的差异。通过试验分析提出该工况下地下粮仓自重抗浮设计的安全储备量，避免浮力过大造成的地下粮仓浮起、外包防水材料拉裂等问题，为地下粮仓抗浮设计修正抗浮设防水位、采用配重法、抗浮锚杆、抗浮桩等方法提供理论指导。

1 回填工况地下粮仓的力学模型

图1 地下粮仓浮力力学模型

仅考虑地下粮仓自重及地下水的作用，地下粮仓在自重作用下理论抵抗浮力为

考虑其他抗浮有利因素，地下粮仓实际抵抗浮力为

2 试验方案

2.1 试验装置

试验装置由模型池，地下粮仓模型筒，数据采集系统3部分组成，试验装置如图2所示。

1.水位标尺 2.水位管 3.模型池 4.模型筒 5.粗砂 6.型钢 7.压力传感器 8.高度调节装置 9.约束横梁 10.位移计 11.200 mm厚二八灰土

1.Water level gauge 2.Water level tube 3.Model pool 4.Model cylinder 5.Coarse sand 6.Profile steel 7.Pressure sensor 8.Height adjustment device 9.Constraint beam 10.Displacement gauge 11.200 mm thick 2:8 lime soil

图2 试验装置图

Fig.2 Test device diagram

模型池用钢化玻璃拼装而成，尺寸为2 000 mm× 2 000 mm×1 000 mm，模型池上端设置一根约束横梁，在上面打2个孔用螺栓焊接一块铁板，用于调节模型筒的高度以及固定压力传感器，在模型池底部开设一个排水口，便于排水，沿模型池对角线方向设置两根水位管和标尺，便于观察和测量水位，模型池四周用型钢来支撑提高整个装置的承载力。

地下粮仓模型筒用聚丙烯塑料板制作，直径分别为400、500、600 mm。为了模拟地下粮仓材质，在模型筒表面涂刷一层水泥砂浆，模型筒参数见表1。

数据采集系统由压力传感器、位移计、DH3821静态应变测试仪、计算机组成。压力传感器固定于模型筒和约束横梁之间，用来测量模型筒上浮时约束反力，量程为200 kg，灵敏度系数为2.0；位移计通过磁性底座固定在约束横梁上，用来测量地下圆形粮仓模型筒的竖向位移，量程为±100 mm，灵敏度系数为2.0；DH3821静态应变测试仪能连续准确稳定的采集试验时压力传感器及位移计读数。

表1 模型筒参数一览表

2.2 试验材料

试验用的土体材料为二八灰土和粗砂。二八灰土按照石灰与普通粘土体积比为2:8进行搅拌，用于地下模型筒筒壁外200 mm范围内回填。模型池内其他位置均用透水性较好的粗砂回填，试验时对二八灰土做土工试验[32]，测得的参数见表2，其干密度和含水率均符合回填土要求。

表2 二八灰土土样物理参数测定表

2.3 试验内容

分别完成直径400、500、600 mm的纯水试验与二八灰土回填试验，共计6组。纯水试验的目的是对试验仪器进行调试与校准，并验证试验装置的可行性。在调试与校准试验仪器后，进行二八灰土回填试验。

2.3.1 试验装置力学模型

在试验过程中，缓缓注水控制水流速度与大小，假定模型池内水为静止状态，近似假定模型筒处于平衡状态，结合试验装置，模型筒状态有2种：状态1为模型筒静止未起浮；状态2为模型筒起浮至平衡；模型筒竖向受力分析如图3所示。

图3 地下粮仓模型筒受力示意图

状态1时模型筒静止未起浮，表达式见式（3）

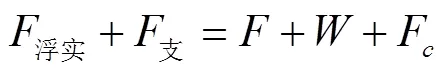
状态2时为模型筒起浮至平衡，表达式见式（4）

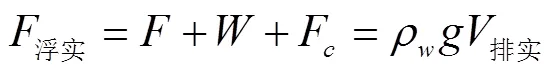
2.3.2 纯水试验

将模型筒A、B、C分别置于模型池底部，安装压力传感器和位移计，缓缓注水，至模型筒浮起一定高度。

2.3.3 二八灰土回填试验

注水管呈环状置于模型池底部，注水管每隔5 cm开一个出水孔；模型池底预铺粗砂，放置模型筒于模型池中间；回填粗砂及二八灰土，距模型筒仓壁周围200 mm范围内回填二八灰土，其余位置均回填粗砂，每10 cm压实一次，至模型池底约60 cm高。安装压力传感器、位移计，静置一周；压力传感器、位移计调零；注水试验至模型筒浮起（见图4），控制注水速度和流量；记录水位，监测压力传感器和位移计读数，待模型筒浮起后拆除试验装置，试验结束。

图4　回填二八灰土试验

3 试验结果与分析

3.1 纯水试验分析

据测试水位，绘制实际浮力曲线与（+）曲线，见图5。其中实际浮力曲线根据观测到的水位按阿基米德定律计算绘制；按测量的模型筒自重和采集的约束反力（将约束反力也折算为自重）绘制（+）曲线。（注：模型池底对模型筒有向上的支承力，试验时未测量，当模型筒开始上浮后模型池池底对模型筒支承力为0。模型筒上浮后（+）即为理论浮力曲线）

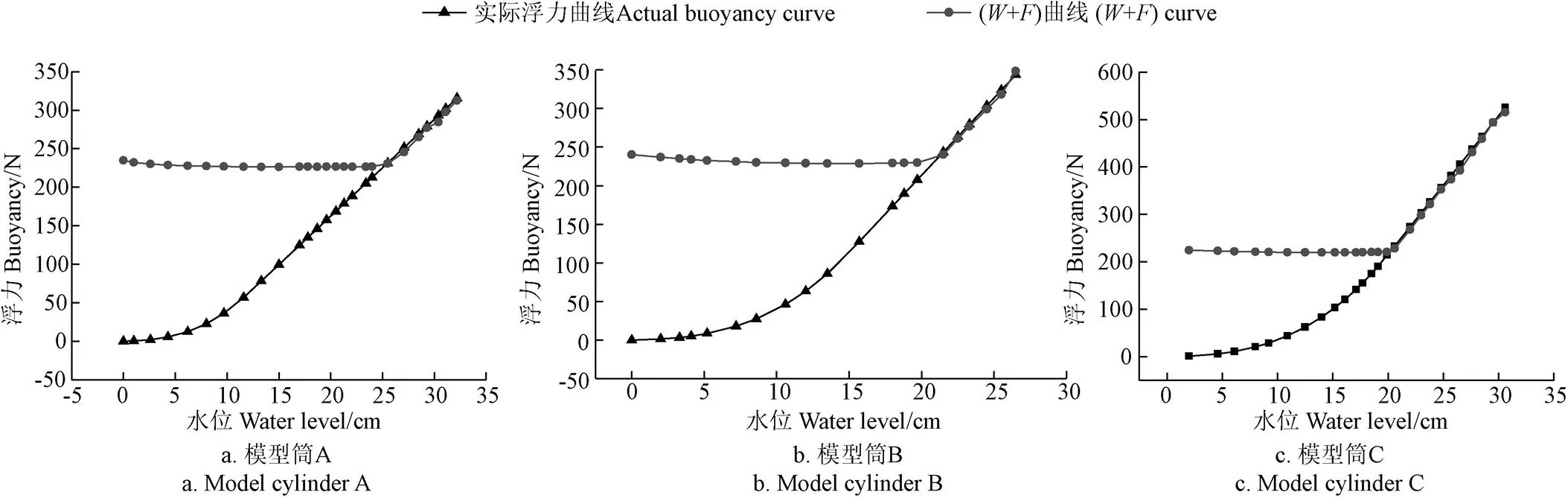
图5 模型筒A、B、C理论浮力曲线与（W+F）曲线图

由图5模型筒A、B、C自起浮水位25.5、21.5、19.9 cm之后，实测浮力与理论浮力（+）基本一致，误差分别在0.03%、1%、3%之内，该装置满足试验要求。并将3个模型筒的纯水起浮水位作为理论起浮水位。

3.2 二八灰土回填试验分析

3.2.1 位移计读数与水位关系分析

根据观察水位与所采集的位移计读数，绘制模型筒A、B、C的水位-位移曲线，见图6。所以在模型筒A底部铺设3.4 cm粗砂、模型筒B底部铺设7 cm粗砂、模型筒C底部铺设70 cm粗砂，所测量实际水位均用观测到的水位值减去所铺设粗砂层厚度。位移计读数为2个位移计测量值的平均值。

图6 模型筒A、B、C的水位-位移曲线图

由图6可知，模型筒A自水位11.1 cm开始监测位移计读数，此时位移计读数为4.98 cm，当水位上升至40.6 cm时，位移计读数为5.01 cm，当水位由40.6 cm上升至67.2 cm时，位移计读数由5.01 cm迅速增加至6.17 cm。模型筒B自水位11 cm开始监位移计读数，此时位移计读数为−0.575 mm，随着水位上升至39 cm，位移计读数增加至−0.23 cm，当水位由39 cm上升至57 cm时，位移计读数由−0.23 cm迅速增加至2.39 cm。模型筒C自水位7 cm开始监测位移计读数，此时位移计读数为0，随着水位上升至33.1 cm位移计读数增加至0.125 cm，当水位由33.1 cm上升至56.5 cm时，位移计读数由0.125 mm迅速增加至8.82 cm。

由位移数据分析，随着水位上升，位移计读数先缓慢减小再缓慢增加，原因是在地下水作用下，模型筒底部粗砂和周边二八灰土沉降导致模型筒位移减小，随着水位上升模型筒受浮力的作用位移缓慢增加。模型筒A、B、C初期位移变化幅度在2 mm之内，认为模型筒处于静止状态。结合纯水试验，当水位分别超过模型筒A、B、C纯水试验起浮水位15.1、17.5、13.2 cm后即模型筒A、B、C实际水位为40.6、39、33.1 cm时位移计读数迅速增大，说明模型筒开始起浮。

3.2.2 压力传感器读数与水位的关系分析

根据观察水位与所采集的压力传感器读数，绘制模型筒A、B、C的水位-约束反力曲线，见图7。

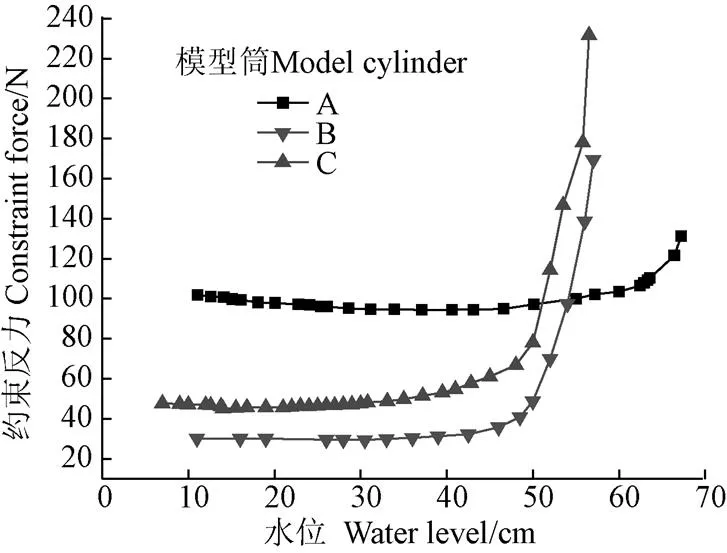
图7 模型筒A、B、C的水位-约束反力曲线图

由图7可知，模型筒A自水位11.1 cm开始监测约束反力，此时为101.84 N，随着水位上升至37.1 cm，下降至94.37 N，当水位由37.1 cm上升至67.2 cm时，由94.37 N迅速增加至131.14 N。模型筒B自水位110 mm开始监测约束反力，此时为30.21 N，随着水位上升至30.5 cm，下降至29.47 N，当水位由30.5 cm上升至57 cm时，由29.47 N迅速增加至169.37 N。模型筒C自水位7 cm开始监测约束反力，此时为47.67 N，随着水位上升至24 cm，下降至46.23 N，当水位由24 cm上升至56.5 mm时，由46.23 N迅速增加至231.69 N。

由约束反力数据分析，水位至模型筒底部时，开始采集压力传感器读数，随着水位上升，约束反力先缓慢减小，原因是在地下水作用下，模型筒底部粗砂与周边回填的二八灰土沉降，随着水位上升模型筒受浮力的作用约束反力缓慢增加。当水位分别超过模型筒A、B、C纯水试验起浮水位11.6、9、4.1 cm后即模型筒A、B、C实际水位为37.1、30.5、24 cm时约束反力迅速增大，说明模型筒开始起浮。

3.2.3 约束反力与位移对比分析

对比位移计读数与约束反力，模型筒的约束反力与位移变化大体上一致。但位移对应的水位拐点与约束反力对应的水位拐点存在一定的滞后性，模型筒A、B、C位移迅速增大的水位要比约束反力迅速增大的水位分别滞后3.5、8.5、9.1 cm。分析是由于其他抗浮综合力（模型筒周侧摩阻力、模型筒底粘滞力、负孔压等即式（2）中F）综合作用所致。实际工程中我们可以以约束反力对应的水位拐点为警戒水位，以位移对应的水位拐点作为实际起浮水位，以保证工程的相对安全，防止因浮力过大造成地下粮仓失稳倾覆。

4 浮力分析

4.1 理论水位、警戒水位、起浮水位浮力计算

根据试验结果，绘制模型筒水位、位移、约束反力读数表。

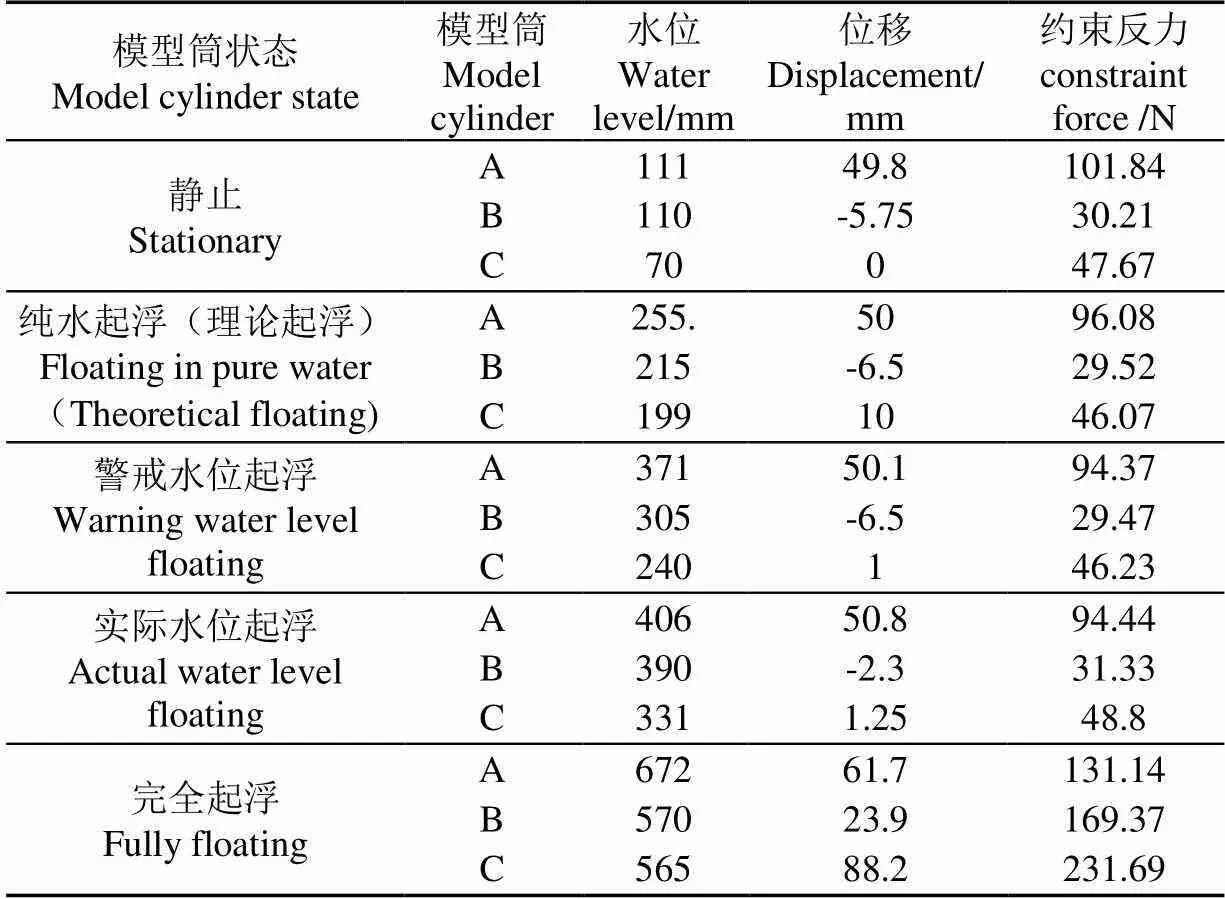
表3 模型筒水位、位移、约束反力读数

以3个模型筒约束反力对应的水位拐点，即约束反力发生突变时的水位作为警戒水位，此时约束反力不再减小。位移对应的水位拐点，即位移发生突变时来确定模型筒的实际起浮水位，此时约束反力与位移都不再减小。确定模型筒A、B、C的警戒水位分别为37.1、30.5、24 cm，确定模型筒A、B、C的起浮水位分别为40.6、39、33.1 cm。

通过试验各个阶段测量的水位来计算浮力，由于上部约束横梁对模型筒产生的约束反力，将其折算成模型筒自重，计算3个模筒在警戒水位和实际起浮水位时的理论抵抗浮力和实际抵抗浮力，见表4。

表4 模型筒水位浮力表

4.2 浮力调整

由式（2）、（4）结合表3、表4模型筒的水位浮力计算，在警戒水位时，模型筒A、B、C实际抵抗浮力为理论抵抗浮力的1.93、2.43、1.66倍。在实际起浮水位时，模型筒A、B、C实际抵抗浮力为理论抵抗浮力的2.15、3.36、2.96倍。根据工程结构抗浮安全系数在1.05～1.1之间[33]，以试验计算得到的下限值对地下粮仓抵抗浮力进行调整，建议在回填二八灰土工况下地下粮仓在预警水位时实际抵抗浮力为理论抵抗浮力的1.5倍，实际起浮水位时实际抵抗浮力为理论抵抗浮力的2倍。

5 结 论

通过对地下粮仓模型筒进行纯水试验与回填二八灰土试验，分析模型筒整个上浮过程中竖向位移与约束反力的变化，以直径为400（模型筒A）、500（模型筒B）、600 mm（模型筒C）为例，计算出模型筒各个状态时的理论抵抗浮力与实际抵抗浮力，得出以下结论：

1）位移变化滞后于约束反力变化，以约束反力的突变值对应的水位作为警戒水位，以位移的突变值对应的水位作为实际起浮水位。

2）在警戒水位时，模型筒A、B、C实际抵抗浮力为理论抵抗浮力的1.93、2.43、1.66倍。

3）在实际起浮水位时，模型筒A、B、C实际抵抗浮力为理论抵抗浮力的2.15、3.36、2.96倍。

4）根据工程结构抗浮安全系数保守的对浮力调整，在回填二八灰土工况下地下粮仓在预警水位时实际抵抗浮力为理论抵抗浮力的1.5倍，实际起浮水位时实际抵抗浮力为理论抵抗浮力的2倍。

[1] 蒋敏敏，陈桂香. 基于应力路径试验的小麦粮堆力学特性和应力应变关系模型[J]. 农业工程学报，2018，34(7)：280－287.

Jiang Minmin, Chen Guixiang. Mechanical properties and stress strain model for bulk wheat based on stress path test[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 280－287. (in Chinese with English abstract)

[2] 蒋敏敏，郭祝辉. 竖向压力和剪切速率对小麦直剪强度及剪胀特性的影响[J]. 农业工程学报，2017，33(6)：275－280.

Jiang Minmin, Guo Zhuhui. Effects of vertical pressure and shear velocity on direct shear strength and dilatancy properties of wheat[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(6): 275－280.(in Chinese with English abstract)

[3] 王振清. 粮仓建筑基本理论与设计[M]. 郑州：河南科学技术出版社，2015.

[4] 刘海燕，王振清，陈雁. 绿色生态储粮仓型：地下粮仓[J].农业机械，2012，5(24)：114－118.

Liu Haiyan, Wang Zhenqing, Chen Yan. Green ecological storage granary type: Underground granary[J]. Agricultural Machinery, 2012, 5(24):114－118. (in Chinese with English abstract)

[5] 袁世民. 地下粮仓[M]. 北京：中国建筑工业出版社，1979.

[6] 郑培，王振清，余汉华. 我国地下仓的简史及特点[J]. 粮油加工，2009(1)：90－94.

Zheng Pei, Wang Zhenqing, Yu Hanhua. A brief history and characteristics of underground granaries in China[J]. Cereals and Oils Processing, 2009(1): 90－94. (in Chinese with English abstract)

[7] 余汉华，王录民，王振清，等. 我国地下粮仓应用的现状及前瞻[J]. 河南工业大学学报，2008，29(6)：79－81.

Yu Hanhua, Wang Lumin, Wang Zhenqing, et al. Present condion and outlook for underground silos[J]. Journal of Henan University of Technology 2008, 29(6): 79－81. (in Chinese with English abstract)

[8] 李伟，狄育慧. 地下粮仓的发展与节能优势[J]. 粮食科技与经济，2015，40(1)：45－47.

Li Wei, Di Yuhui. Development and energy saving advantages of underground granary[J]. Grain Science and Technology and Economy, 2015, 40(1): 45－47. (in Chinese with English abstract)

[9] 张会军，刘海燕，张庆章. 砂土中地下粮食圆形筒仓抗浮模拟实验研究[J]. 粮油食品科技，2017，25(2)：99－104.

Zhang Huijun, Liu Haiyan, Zhang Qingzhang. Simulation experiment of anti-floating of Underground grain silos in sandy soil[J]. Science and Technology of Cereals, Oils and Foods, 2017, 25(2): 99－104. (in Chinese with English abstract)

[10] 李广信. 关于有效应力原理的几个问题[J]. 岩土工程学报，2011，33(2)：315－320.

Li Guangxin. Some problems about principle of effective stress[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(2): 315－320. (in Chinese with English abstract)

[11] 李广信，吴剑敏. 关于地下结构浮力计算的若干问题[J].土工基础，2003，17(3)：39－41.

Li Guangxin, Wu Jianmin. Some problems about the calculation of uplift force on underground structures [J].Soil Eng. and Foundation 2003, 17(3): 39－41. (in Chinese with English abstract)

[12] 方玉树. 基于水压率讨论土中孔隙水压力及有关问题[J].岩土工程界，2007，10(5)：21－26.

Fang Yushu. Based on the water pressure ratio, the pore water pressure and related problems in soil are discussed[J].Geotechnical Engineering World, 2007, 10(5): 21－26. (in Chinese with English abstract)

[13] 饶清. 武汉地区地下建筑抗浮设计水位取值与浮力折减分析[J]. 武汉勘察设计，2012，16(2)：36－38.

Rao Qing. Analysis on the value of anti-floating design water level and buoyancy reduction ofunderground buildings in Wuhan area[J]. Wuhan Investigation &Design, 2012, 16(2): 36－38. (in Chinese with English abstract)

[14] 张欣海. 深圳地区地下建筑抗浮设计水位取值与浮力折减分析[J]. 勘察科学技术，2004，8(2)：12－17.

Zhang Xinhai. Analysis of defence water level and reduction factorof buoyancy for underground buildings in Shenzhen area[J]. Site Investigation Science and Technology, 2004, 8(2): 12－17. (in Chinese with English abstract)

[15] Achari G, Joshi R C, Bentley L R, et al. Prediction of the hydraulic conductivity of clays using the electric double layer theory[J]. Canadian Geotechnical Journal, 1999, 36(5): 783－792.

[16] Singhp N, Wallender W. Effects of adsorbed water layer in predicting saturated hydraulic conductivity for clays with Kozeny-Carman equation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(6): 829－836.

[17] Murat Bikçe, Murat Örnek, Ömer Faruk Cansız. The effect of buoyancy force on structural damage: A case study[J]. Engineering Failure Analysis,2018.

[18] Forbes M, Vogwill R. A geochemical investigation of hydrologically derived threats to rare biota: The Drummond Nature Reserve, Western Australia[J]. Hydrogeology Journal, 2012, 20(1): 167－183.

[19] 王洪新. 水土压力统一计算理论的证明及水土共同作用下的压力计算[J]. 岩石力学与工程学，2012，31(2)：392－398.

Wang Hongxin. Verification of unified calculationtheory of water and earth pressures and calculation of pressure under interaction of water and earth[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 392－398. (in Chinese with English abstract)

[20] 白晓宇，张明义，寇海磊. 基于裸光纤光栅传感技术GFRP抗浮锚杆荷载传递机制的原位试验研究[J]. 工程力学，2015，32(8)：172－181.

Bai Xiaoyu, Zhang Mingyi, Kou Hailei. Field experimental study of load transfer mechanism of GFRP anti-floating anchoes based on embedded bare fiber bragg grating sensing technology[J]. Engineering Mechanics, 2015, 32(8): 172－181. (in Chinese with English abstract)

[21] Yang Jianwen, Feng Zuohai, Luo Xianrong, et al. Numerically quantifying the relative importance of topography and buoyancy in driving groundwater flow[J]. Sci China Earth Sci, 2010, 53(1): 64－71.

[22] Chen Liaojiang，Wang Xiao , Hou Shuli . Anti-floating anchor rods and waterproof construction technology for deep pits[J]. Applied Mechanics and Materials, 2013(353/354/355/356): 952－956.

[23] 赵继红. 浮力的实质[J]. 雁北师范学院学报，2002(2)：89－90.

Zhao Jihong. Talking about substance of buoyancy[J]. Journal of Yanbei Normal University, 2002(2): 89－90. (in Chinese with English abstract)

[24] 唐春华，向伟明，宋肖冰，等. 砂类土层中地下结构浮力的模型试验[J]. 广州大学学报，2013，12(3)：34－37.

Tang Chunhua, Xiang Weiming, Song Xiaobing, et al. Model test of buoyancy for underground structure in sandy- soilstratum[J]. Journal of Guangzhou University, 2013, 12(3): 34－37. (in Chinese with English abstract)

[25] 梅国雄，宋林辉，宰金珉. 地下水浮力折减试验研究[J].岩土工程学报，2009，31(9)：1476－1480.

Mei Guoxiong, Song Linhui, Zai Jinmin. Experimental study on reduction of groundwater buoyancy[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(9): 1476－1480. (in Chinese with English abstract)

[26] 张乾，宋林辉，梅国雄. 黏土地基中的基础浮力模型试验[J]. 工程勘察，2011，39(9)：37－41.

Zhang Qian, Song Linhui, Mei Guoxiong. Model experiment on foundation buoyancy in clay[J]. Geotechnical Investigation & Surveying, 2011, 39(9): 37－41. (in Chinese with English abstract)

[27] 宋林辉，王宇豪，付磊，等. 软黏土中地下结构浮力测试试验与分析[J].岩土力学，2018，39(2)：753－758.

Song Linhui, Wang Yuhao, Fu Lei, et al. Test and analysis on buoyancy of underground structure in soft clay[J]. Rock and Soil Mechanics, 2018, 39(2): 753－758, 2013. (in Chinese with English abstract)

[28] 周明. 不同土层中地下结构抗浮作用的试验研究[D]. 广州：广州大学，2013.

Zhou Ming. Analysis of Test to the Structure Anti-floating in Different Soil[D]. Guangzhou: Guangzhou University. (in Chinese with English abstract)

[29] 张第轩. 地下结构抗浮模型试验研究[D]. 上海：上海交通大学，2007.

Zhang Dixuan. Experimental Study on Anti-floating of Underground Structures[D]. Shanghai: Shanghai Jiao Tong University, 2007. (in Chinese with English abstract)

[30] 李冲. 单一土质中地下钢筋砼粮食圆形筒仓抗浮模拟试验研究[D]. 郑州：河南工业大学，2016.

Li Chong. Model Test Study On Anti-floating of Underground Reinforced Concrete Circular Grain Silos in a Single Soil[D]. Zhengzhou: Henan University of Technology, 2016. (in Chinese with English abstract)

[31] 田栋杰. 二八灰土中圆形地下钢筋混凝土粮仓浮力试验研究[D]. 郑州：河南工业大学，2018.

Tian Dongjie. Experimental Study on Buoyancy of Circular Underground Reinforced Concrete Granary in Lime Soil[D]. Zhengzhou: Henan University of Technology, 2018. (in Chinese with English abstract)

[32] 中华人民共和国国家标准.土工试验方法标准GB/T50123-1999[S]. 北京：中国建筑工业出版社，1999.

[33] 李慧梅，陆景慧，田韶英，等. 不同规范结构抗浮安全系数的比较[J].特种结构，2007，24(2)：40－41.

Li Huimei, Lu Jinghui, Tian Shaoying, et al. Comparision about safety factor of anti-buoyancy of structure for different codes[J]. Special Structures, 2007, 24(2): 40－41. (in Chinese with English abstract)

Buoyancy early warning of underground granary with “2:8 lime soil” backfilling

Liu Haiyan1, Meng Weixin1, Wang Zhenqing1, Tian Dongjie2, Xu Xiangnan1, Liu Xu1

(1.,450001,; 2..,450000,)

The buoyancy of the underground structure is generally calculated on the basis of Archimedes law. However, the influence of surrounding backfilling soil was not taken into account in previous work. This article takes an underground granary that has been constructed as a research object. In this study, the 2:8 lime soil backfilling condition was considered in the indoor scale model tests. The diameters of the underground granary model cylinders were taken as 400 (Model cylinder A), 500 (Model cylinder B) and 600 mm (Model cylinder C), respectively. The whole scale model test consisted of two parts, the pure water test and the 2:8 lime soil backfilling tests. The results of the pure water test indicated that the actual buoyancy calculated based on Archimedes law and the theoretical buoyancy under the self-weight of the model cylinder (including the constrain force of the upper part of the model cylinder, which is also converted into its own weight) were basically consistent. The errors between the actual buoyancy and the theoretical buoyancy for the three models cylinder were 0.03%, 1%, 3%, respectively. In the 2:8 lime soil backfilling test, the water was injected slowly, the displacement was monitored by the displacement meter and the reaction force at the upper surface was measured by the pressure sensor. The numerical variation of displacement and constraint force during the whole process of the model cylinder floating was analyzed. The displacement mutation value lags behind the constraint force mutation value. When the pressure sensor reading changed significantly but the displacement meter reading did not, the actual water level served as the warning water level of the model cylinder. When the pressure sensor and the displacement meter reading changed significantly together, the actual water level was used as the actual floats water level of the model cylinder. Taking the warning water level and the actual floating water level as the theoretical basis for calculation, obtained the theoretical resistance to buoyancy under the self-weight of the model cylinder and the actual resistance to buoyancy. When reaching the warning water level, the actual resistance to buoyancy of model cylinder A, B, C were 1.93, 2.43, 1.66 times respectively as the theoretical resistance to buoyancy. When reaching the actual floating water level , the actual resistance to buoyancy of model cylinder A, B, C were 2.15, 3.36, 2.96 times respectively as the theoretical resistance to buoyancy. When backfilling 2:8 lime soil around an underground granary, calculating the buoyancy using Archimedes' law is safe. Considering the safety reserve comprehensively, the 2:8 lime-soil backfilling condition of underground granary, when reaching the warning water level, the actual resistance to buoyancy is 1.5 times of the theoretical resistance to buoyancy,and when reaching the actual floating water level, the actual resistance to buoyancy is 2 times of the theoretical resistance to buoyancy. The research results are able to provide a reference for the anti-buoyancy design of underground granaries and other underground structures in the future.

buoyancy; water levels; tests; 2:8 lime soil; backfilling conditions; underground granary; water injection test

2019-04-29

2019-05-31

粮食公益性行业科研专项（201413007-01）

刘海燕，副教授，主要从事粮油仓储结构教学、科研工作。Email：hyliu0708@163.com

10.11975/j.issn.1002-6819.2019.11.034

TU923

A

1002-6819(2019)-11-0299-07

刘海燕，孟伟新，王振清，田栋杰，徐向楠，刘 旭. “二八灰土”回填地下粮仓浮力预警试验研究[J]. 农业工程学报，2019，35(11)：299－305. doi：10.11975/j.issn.1002-6819.2019.11.034 http://www.tcsae.org

Liu Haiyan, Meng Weixin, Wang Zhenqing, Tian Dongjie, Xu Xiangnan, Liu Xu. Buoyancy early warning of underground granary with “2:8 lime soil” backfilling[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(11): 299－305. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.11.034 http://www.tcsae.org