高温基线密封编织弹簧管的建模与仿真

巴全坤 王维民 姜 鑫 张登鹏

（高端机械装备健康监控与自愈化北京市重点实验室，北京化工大学，北京 100029）

0 引言

高超声速飞行器是指飞行速度超过5 倍声速的飞机、导弹、炮弹之类的有翼或无翼飞行器，具有突防成功率高的特点，有着巨大的军事价值和潜在的经济价值［1］。高超声速飞行器飞行速度高，由于激波压缩和粘性摩擦作用，壁面周围空气温度会急剧上升，一旦高温气流通过密封部位流入飞行器内部，就会对飞行器内部的不耐温结构造成破坏，因此必须进行有效的热防护［2-3］。目前在高超声速飞行器的活动控制面板处使用的热防护多为高温基线密封，该技术在国外已经比较成熟，但我国仍然处于研究阶段，高温热密封仍然是制约高超声速飞行器发展的关键技术［4］，研究高温基线密封对我国航空航天业的发展具有重要的意义。

美国NASA 曾在20世纪开展了许多高温密封的研究，包括NASA-JSC（X-38 项目）、NASA-ARC（热防护分支）、NASC-KSC（轨道飞行器试验）、波音密封部门（X-38 项目）和Hi-Temp（密封和热防护制造）［5］。高温基线密封主要运用在高声速飞行器的发动机、起落架、舱门、舵、襟翼等处［6-7］。结构分为三层，外层为Nextel 纤维编织的两层护套，中间层为Inconel-750 高温合金编织的弹簧管，内层填充Saffil氧化铝纤维［8］。其中编织弹簧管为主要的弹性元件，其结构类似于纺织学上的纬编织物，通过平行的Inconel-750 高温合金丝编织成环形的立体几何结构。高温基线密封安装在活动部位，需要有良好的弹性来保持与密封缝隙两侧的壁面接触，编织弹簧管作为主要提供回弹性的装置起着至关重要的作用。

本文主要针对高温基线密封的主动预紧力装置编织弹簧管进行仿真分析，研究编织结构与参数对编织弹簧管性能的影响。

1 基线密封设计要求

密封件必须能够在980～1 204 ℃的高温氧化环境中使用，尽量减小热气流泄露到温度敏感部位［9］。密封件一般在压缩状态下安装，保证与活动面板两侧紧密贴合，在密封间隙改变时，密封件要有足够的回弹性来补偿间隙变化，但回弹力过大时容易损坏控制面板上的隔热层，加快结构破坏，同时也会导致控制面板活动所需的驱动力大大增加，因此回弹力要适中。根据密封设计要求（表1）［10］，编织弹簧管需要满足在各温度环境下压缩时的应力尽量小，以避免结构破坏；回弹力尽量大，但不超过最大0.88 N/mm；使用寿命要超过最大使用周期。

表1 密封设计要求Tab.1 Seal design requirements

2 编织弹簧管几何建模

2.1 几何结构

编织弹簧管为圆柱形空间立体几何，为了对编织几何的参数进行度量，将圆柱形的编织弹簧管展开成平面几何进行研究。参考纺织学中的纬编织物结构，采用Pierce线圈模型来模拟编织弹簧管中心线的形状。如图1所示，Pierce 线圈模型分为针编弧、圈柱、沉降弧［11］。

图1 Pierce线圈模型Fig.1 Pierce coil model

Pierce 线圈模型是一种比较理想化的假设，其中包括以下几点［12-13］：

（1）用直线段来模拟圈柱，用圆弧来模拟针编弧和沉降弧；

（2）每个线圈单元为左右对称，且针编弧与沉降弧的半径相等，弧长相等；

（3）线圈各处的截面为圆形，且直径相等。

2.2 结构参数

Pierce 线圈模型由圆形截面和中心线确定，中心线为分段连续光滑曲线，图2为中心线的1/4模型。

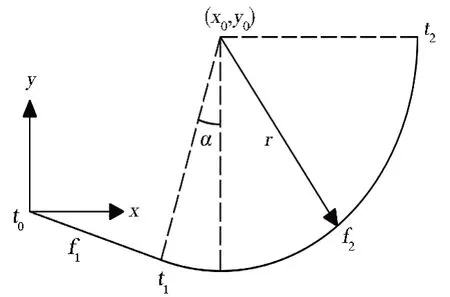
图2 四分之一中心线模型Fig.2 Quarter centerline model

图2中的曲线采用规律曲线根据方程创建，规定t为自变量，取值范围为0～1。该曲线函数分为圈柱中心线函数f1(t)和针编弧中心线函数f2(t)。 圈柱中心线f1(t)的方程：

针编弧中心线f2(t)的方程：

式中：

将图2中的1/4 曲线进行对称与阵列，得到图3所示的编织弹簧管中心线的平面展开图。

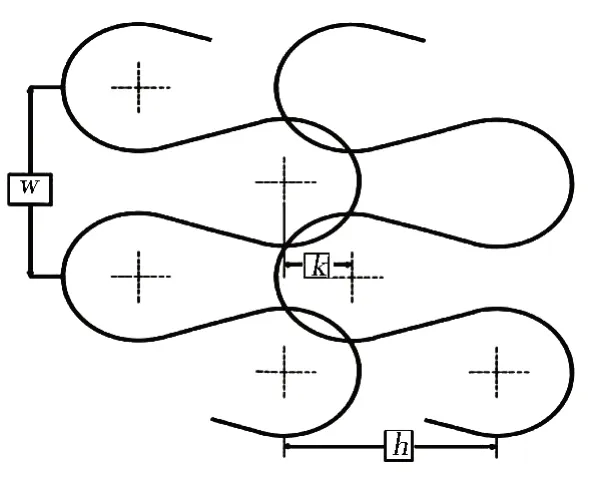
图3 中心线的平面展开图Fig.3 Plane plan of centerline

w为两个沉降弧圆心之间的距离：

D为编织弹簧管的直径；n为一周Pierce 线圈的数量。

圆心坐标(x0，y0)由以下表达式计算：

参数t2为最终变量，当t在0～1 上变化时，函数f1(t)和f2(t)正好组成完整的1/4 模型。t2有如下关系式：

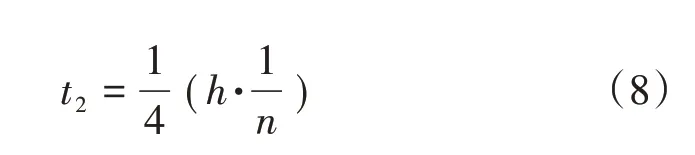
方程（9）、（10）满足连续性条件：

方程（11）、（12）满足光滑性条件：

tb=t2时，x′2= 0，得到如下表达式：

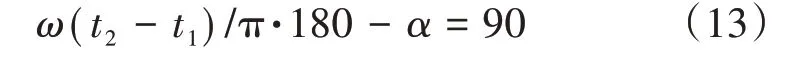
此时有5 个约束方程（9）～（13）和5 个未知数t1、w、α、a、b，故方程有唯一确定的解。

弹簧的刚度还与编织结构有关，编织结构可用环密度LD来度量，其定义公式如下：

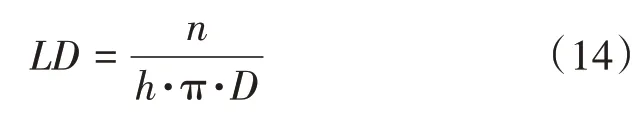
对于编织弹簧管的剩余参数在设计时指定，具体参数如表2所示。将中心线平面曲线缠绕到圆柱面上，得到针编弧与沉降弧的交点，将交点沿着圆柱的半径方向偏移一个线径d，构造型值点，通过型值点创建空间非均匀有理B 样条曲线（NURBS），然后采用光顺曲线串方法让针编弧与圈柱光滑相接。最终得到编织弹簧管的三维模型。

计算时忽略两端的边界效应。根据基线密封安装环境，在弹簧管的上下端各添加一个平板，通过平板的移动来模拟编织弹簧管的压缩，如图4所示。

表2 编织弹簧管参数Tab.2 Parameters of braided spring tube

图4 计算模型Fig.4 Computational model

3 材料特性、网格和边界条条件

3.1 材料特性

Inconel X-750为镍基高温合金，在800 ℃以下具有较高的强度。假设材料为线弹性的，其材料参数如表3所示。

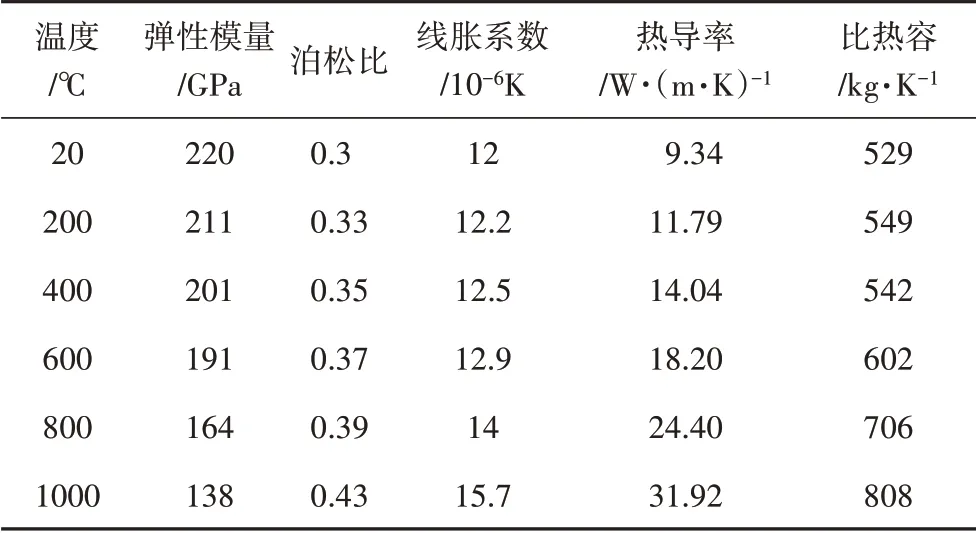
表3 Inconel X-750材料参数［14］Tab.3 Material parameters of Inconel X-750

3.2 网格和边界条件

模型网格均采用扫掠网格画法，网格均为高精度的六面体网格，单元采用高阶三维20 节点的solid186单元，单元保留中间节点。

编织弹簧安装在两平板之间，一个固定，另一个给定位移，用来模拟弹簧管的压缩过程，该过程分为多个子步施加。接触约束采用自动识别，自动检测公差值为0.01 mm，接触检测类型为面与面接触检测。绑定接触的接触算法采用纯罚函数算法。摩擦接触和无摩擦接触为非线性接触，收敛困难，均采用增广拉格朗日算法。

4 结果分析

通过提取上盖板随位移变化的回弹力来绘制编织弹簧的位移-载荷曲线，进而对弹簧的刚度进行评估。

4.1 不同接触类型的影响

针对环密度LD=0.05 和LD=0.10 模型，分别计算了无摩擦、摩擦因数为0.1和绑定等不同接触状态对弹簧刚度的影响，计算结果如图5～图6所示。

图5 LD=0.05时不同接触类型的影响Fig.5 Effects of LD=0.05 different contact

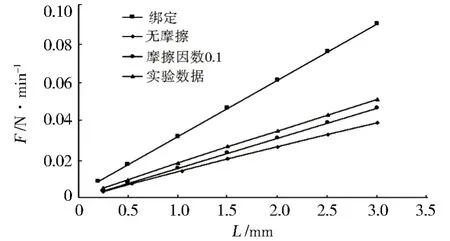
图6 LD=0.10时不同接触类型的影响Fig.6 Effects of LD=0.10 different contact

由计算结果可以看出，不管在何种接触状态下，编织弹簧的回弹力与压缩量都呈现出线性关系。选择接触摩擦因数为0.1的结果与实验结果吻合较好。在压缩量低于1 mm 时，无摩擦接触和摩擦接触的结果相差很小，接触之间的摩擦力对弹簧刚度的影响很小。绑定接触使编织弹簧的刚度大大增加，其计算结果与实验结果相差甚远。

4.2 不同环密度的影响

由环密度LD的定义公式可以看出，环密度越大，编织越密集，计算了LD=0.05 和LD=0.10 模型。在接触同为摩擦因数为0.1的结果如图7所示。

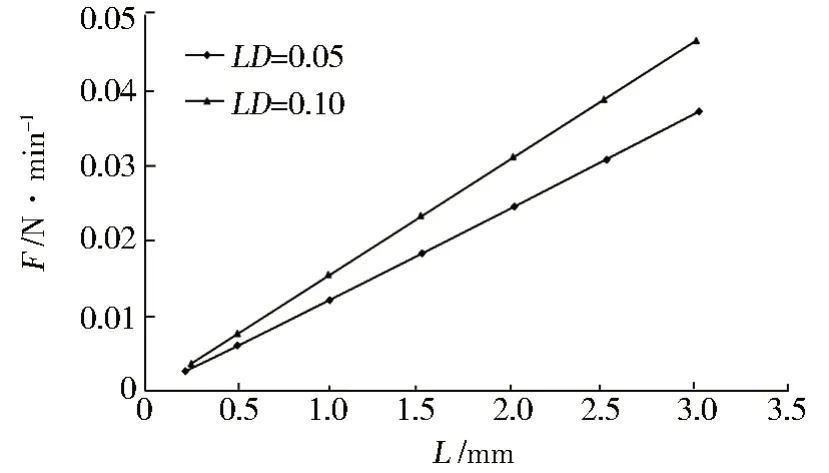
图7 环密度的影响Fig.7 Influence of ring density

从计算结果可看出，通过增加环密度对弹簧刚度的影响较小，在3 mm的压缩量下，环密度LD=0.10模型比环密度LD=0.05模型的回弹力高约20%。

4.3 不同线径的影响

针对环密度LD=0.05 的模型，分别对线径为0.23、0.32、0.40 mm的模型进行计算，得到的结果如图8～9所示。

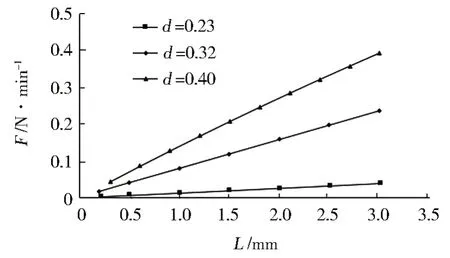
图8 线径对刚度的影响Fig.8 Effect of wire diameter on stiffness

图9 线径对应力的影响Fig.9 Effect of wire diameter on stress

某一线径下编织弹簧回弹力与压缩量仍然呈线性关系，但不同线径下弹簧的回弹力与线径表现为非线性高次关系，回弹力随着线径的增加急剧地增加。线径从0.23 变到0.32 mm，回弹力增加了约6倍；线径从0.23 变到0.40 mm，回弹力增加了约11倍。但随着线径的增加，在同样压缩量下的最大应力也急剧增加，应力过大会造成结构破坏，故线径的选择也不宜过大，推荐使用0.32mm的线径。

4.4 不同编织股数的影响

本次计算模型均为单股编织，故需要将多股编织简化成单股编织。通过等效面积法来确定单股编织的直径，等效公式如下：

式中，d为单股线径，N为多股编织时的股数，d′为多股编织时等效成单股编织的直径。

等效面积下单线模型与多股编织模型相比，其结构是连续的，受力均匀，故其刚度要比多股编织模型高，因此必须对单股模型的刚度进行修正。假设多股编织的弹簧线之间的影响可以忽略不计，在受力弯曲时，弹簧线截面上的剪力对弯曲变形的影响可以忽略，故对单股模型进行修正时将其简化成纯弯曲结构。纯弯曲静力平衡公式：

根据等效原则，多股编织模型和单股模型在相同压缩量下，其变形后的曲率1/ρ、所承受的弯矩M、抗弯刚度EI均应相等。假设EI为多股编织模型中每股的抗弯刚度，则多股编织的抗弯刚度E1I1=NEI，即I1=NI。圆形截面的截面惯性矩公式如下：

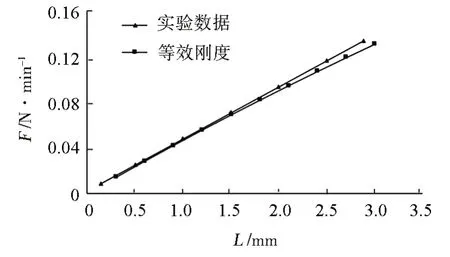
图10 刚度修正Fig.10 Influence of wire number

不同编织股数采用等效面积与等效刚度后的计算结果如图11所示。

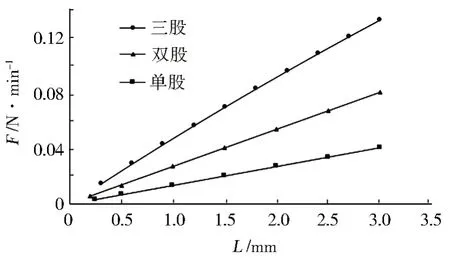
图11 不同编织股数的影响Fig.11 Effect of the number of braided strands

从计算结果可以看出，增加编织股数，单位长度回弹力明显增加，从单线变双线，回弹力增加2.13倍，从单线变三线，回弹力增加3.54倍。但是随着编织股数的增加，应力也快速增大，因此编织股数也不宜过多，推荐使用双线编织。

4.5 不同温度的影响

为了研究温度对弹簧刚度的影响，对环密度LD=0.05 的编织弹簧管计算其在常温、200、400、600、700、800、900、1 000℃下压缩3 mm 时的回弹力，得到如图12的计算结果。

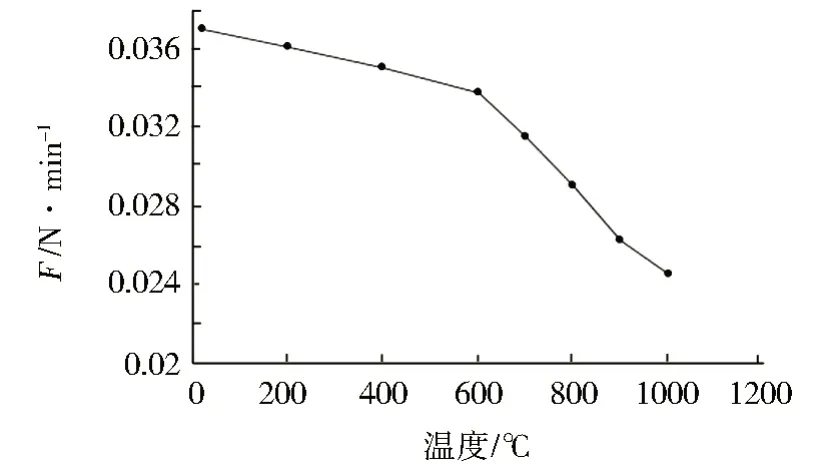
图12 温度的影响Fig.12 Influence of temperature

由计算结果可以看出，随着温度的升高，编织弹簧管的回弹力逐渐下降，其在600 ℃以下时，回弹力下降的速度相对较小，在600～900 ℃时，下降速度明显增加，在高于900 ℃后，回弹力的下降速度有所减小，但仍然比温度在600 ℃以下时的下降速度快。

4.6 疲劳寿命

环密度LD=0.05 的编织弹簧管在650 ℃下的静力分析结果如图13～14所示。

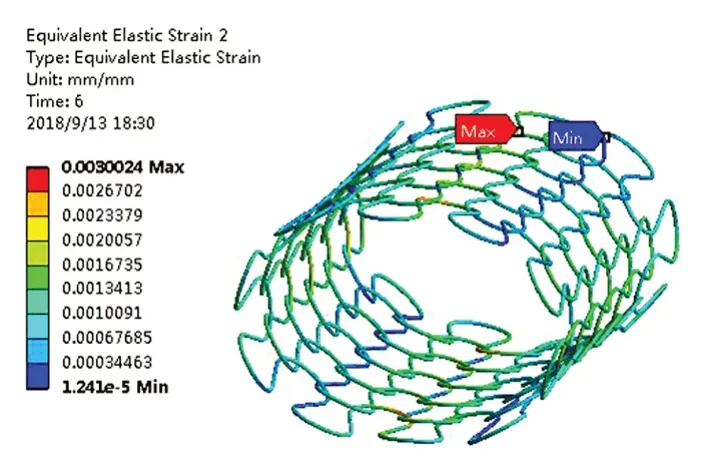
图13 应变云图Fig.13 Strain nephogram

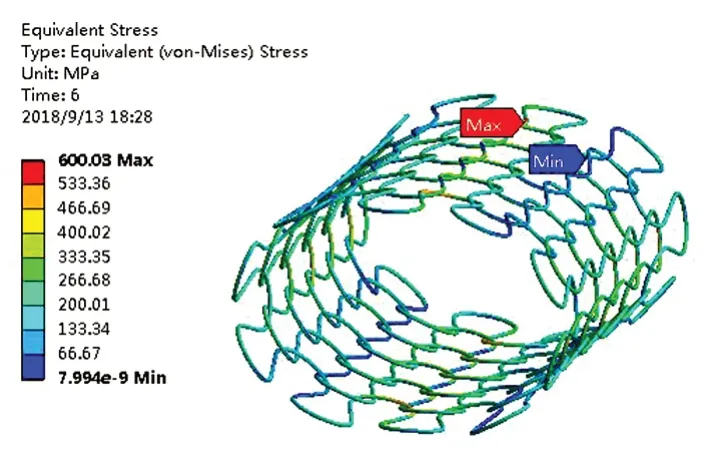
图14 应力云图Fig.14 Stress nephogram

由图可知，最大应变为0.3%（较小），最大应力为600 MPa（较大），因此疲劳计算时采用应力-寿命曲线（S-N曲线）来表示应力与失效循环的关系。采用国产GH4169高温镍基合金在总应变范围为1%时的S-N曲线来代替计算，S-N曲线如图15所示［15］。

图15 S-N曲线Fig.15 S-N curve

疲劳载荷类型选用脉动循环定义，设计寿命为106。计算得到的疲劳寿命云图如图16所示。

图16 寿命云图Fig.16 Life nephogram

由图可以看出，编织弹簧管的最小寿命发生在编织弹簧最高与最低的针编弧上，最小寿命为898次循环，满足密封设计要求。

5 结论

参照Pierce 线圈模型对编织弹簧管进行参数化建模，对比有限元计算结果与实验数据，该模型可有效地对弹簧刚度进行预测。接触面摩擦因数为0.1时能较好吻合实验结果。

（1）弹簧刚度对线径十分敏感，回弹力与线径表现为非线性高次关系，增大线径能获得很大的刚度增强。如果设计的弹簧管回弹力不够，通过增加线径能得到很好的效果。

（2）对多股编织模型可通过等效面积与等效刚度转化成单股编织模型，能使建模与计算大大简化。从单线变成多线编织，回弹力成倍增加。

（3）温度低于600 ℃时弹簧的刚度变化很小，高于600 ℃后，弹簧刚度随着温度升高快速下降，这与材料的高温特性有关，可以通过选用更耐温的材料来进行改善。

（4）通过S-N曲线计算的最低疲劳寿命高于密封设计要求，该计算可为编织弹簧管的合理使用提供有利参考。

（5）为满足编织弹簧管在各温度下压缩时的应力尽量小、回弹力尽量大、但不超过最大0.88 N/mm的设计要求，推荐使用环密度LD=0.05、线径为0.32 mm、双线编织的参数来制作编织弹簧管。