基于LMD和MSEE的滚动轴承复合故障特征提取方法

王普，李天垚，高学金，高慧慧

(1.北京工业大学 信息学部，北京 100124； 2.数字社区教育部工程研究中心，北京 100124；3.城市轨道交通北京实验室，北京 100124；4.计算智能与智能系统北京市重点实验室，北京 100124)

滚动轴承是机械设备的重要部件之一，其使用方式多样且用途广泛，在机械设备运行中起着不可或缺的作用，但轴承也是极易出现故障的部件，有必要对其运行状态进行监测[1]。

在实际运行中，由于现场设备和环境的干扰，轴承振动信号的故障特征难以提取，影响故障诊断的结果，需要对信号进行预处理[2]。

另外，轴承长时间运行在恶劣的工程环境中，单一故障很容易引发其他故障，以复合故障的形式存在，故障诊断的关键是加大复合故障特征的区分度[3-4]。文献[5]用小波包的频段能量作为轴承复合故障的特征向量，但其对故障特征的描述不够充分。文献[6]用多小波系数分支构造特征图，但对于多小波变换，由于涉及到多个小波基函数，且小波基函数和分解层数难以确定，会对结果产生影响。文献[7]提出了基于陷波器的自适应复合故障诊断方法，需要采用频谱分析法辨别轴承的故障特征，对人的依赖性较大。文献[8]用时间序列的多尺度熵反映信号复杂度，文献[9]将信号各频段内能量的变化作为识别故障信息的依据，对轴承单一故障的诊断均取得了良好的效果。

针对信号预处理和故障特征区分度的问题，提出了一种基于局域均值分解(Local Mean Decomposition，LMD)[10-12]和多尺度熵能量(Multi-Scale Entropy Energy，MSEE)的轴承复合故障特征提取方法，通过LMD处理降低噪声的干扰，从时间序列的动力学参数与能量两方面考虑，构建MSEE的特征向量以全面表征故障特点，解决复合故障信号强弱不均、相互耦合的问题。

1 局域均值分解

考虑到实际采集的轴承信号中夹杂着噪声干扰，与真实信号存在一定的差别，如果不对噪声进行处理，噪声成分也将参与特征提取，导致结果产生偏差，因此采用LMD方法对原始信号进行分解与重构，降低噪声的干扰。

LMD实质是将原始信号分解成一系列具有物理意义的PF分量与残余项之和，每个PF分量可表示为1个表现瞬时幅值的包络信号和1个纯调频信号的乘积，对应着原始信号的时频分布，通过对原始信号进行LMD处理可以降低噪声等其他成分的干扰，得到更准确的真实信号，其具体的算法步骤如下。

1)对于原始振动信号x(t)，找出其所有的极值点ni，并求出相邻2个极值点的局部均值mi和局部包络ai， 即

(1)

(2)

2)用滑动平均法分别求取mi和ai对应的局部均值函数m11(t)和局部包络函数a11(t)。

3)将局部均值函数m11(t)从原始振动信号x(t)中分离，得到h11(t)为

h11(t)=x(t)-m11(t)。

(3)

4)对h11(t)进行解调可得

s11(t)=h11(t)/a11(t)。

(4)

重复上述步骤得到有关s11(t)的局部包络估计函数a12(t)。若a12(t)=1，则证明s11(t)为纯调频函数；若a12(t)≠1，则需要将s11(t)重复上述解调过程直至a1(n+1)(t)=1，使s1n(t)为一个纯调频信号。

5)累乘所有的局部包络函数，则包络估计函数a1(t)为

(5)

6)a1(t)与s1n(t)的乘积为第1个PF分量，即

FPF1(t) =a1(t)s1n(t)，

(6)

由s1n(t)可以求出瞬时频率为

(7)

7)分离x(t)与FPF 1(t)得到u1(t)，将u1(t)重复上述步骤k次，直到uk为一个单调函数，即

(8)

最后，x(t)分解为k个PF分量与1个单调信号uk之和，即

(9)

2 多尺度熵能量

采集轴承振动信号的加速度传感器一般固定于轴承座上。对于外圈故障，由于外圈不随转子转动，只有在转子经过故障处时才会有幅值脉冲，外圈故障信号表现为周期性的脉冲，其振动幅值不变；对于内圈故障，由于内圈随转子转动，传感器的位置保持不变，内圈故障信号表现为一系列幅值不等的周期脉冲；对于滚动体故障，由于滚动体不止要随转子进行转动，其本身还会自转，滚动体故障信号表现为不平稳的随机脉冲。

单一轴承故障演变为复合轴承故障是故障特征相互耦合的结果，并不是简单的叠加。一旦变成复合故障，不同故障之间强弱不均、特征不易区分。复合故障与单一故障有相似性，只采用一种特征提取方法作为指标时，很容易造成结果的误报和漏报。因此，将多尺度熵和能量结合起来构建MSEE可以全面表征轴承复合故障中的特征。

2.1 多尺度熵

多尺度熵(Multi-Scale Entropy，MSE)为不同尺度下时间序列粗粒化后的样本熵，代表各尺度下时间序列的复杂程度，其反应了时间序列的自相似性[13]，随着尺度增加呈现的变化趋势可以作为区分信号复杂度的依据。时间序列的复杂度对应其规律性，序列的无规则程度越高，其熵值就越大，也代表原始序列越复杂，例如白噪声；如果序列呈现一定的规律性，那么其熵值就越小，例如有周期脉冲的信号。多尺度熵的值与信号幅值无关，也不受机械设备工频的影响，因此对机械设备的故障诊断具有普适性。多尺度熵的基本计算步骤如下。

1)对于长度为N的原始时间序列Xi={x1,x2,…,xN}。预先给定一个相似容限r和嵌入维数m，构建新的连续粗粒化时间序列，即

(10)

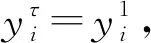
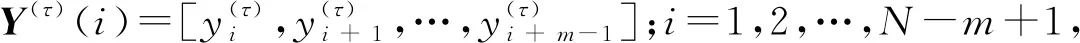
3)将Y(τ)(i)和Y(τ)(j)对应元素之间差值最大值的绝对值定义为两者之间的距离，即

d(τ)[Yτ(i),Yτ(j)]=max|y(τ)(i+k)-

y(τ)(j+k)|，

(11)

式中：k为0～(m-1)之间的整数，i≠j。

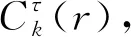
(12)

(13)

5)对m+1维的矢量，重复上述步骤得到m+1维的Cτ,m+1(r)。

6)对于长度为N的时间序列，其样本熵为

lnCτ,m(r)-lnCτ,m+1(r)，

(14)

则多尺度熵可表示为

EMSE={τ|ESampEn(m,r,N)}=

{τ|lnCτ,m(r)-lnCτ,m+1(r)}。

(15)

分析可知，影响多尺度熵的参数有尺度因子τ、相似容限r、嵌入维数m和序列长度N，这些参数的取值还没有统一的标准，一般情况下取m=2，r为0.1～0.25倍的原始时间序列标准差σ，N需要足够大[14]。

多尺度熵反应的是时间序列的规律性和自相似性。有些复合故障是单一故障的矢量叠加[15]，与单一故障相比，时间序列的规律性较为相似。对于这种规律性和自相似性不易区分的时间序列，仅仅依靠多尺度熵作为特征提取指标时，很容易造成结果的误判。

2.2 多尺度熵能量

为了克服多尺度熵的缺陷，在考虑时间序列动力学特性的基础上考虑时间序列的能量波动。当时间序列额外产生脉冲时，在相同频带内能量会发生较大的变化，这个能量的变化与脉冲的振幅、频率成正比。对于时间序列Xi={x1,x2,…,xN}，其能量为

(16)

能量分布的差异性可以反应时间序列的信号特征，其可单独作为机械设备故障诊断的指标。但对于复合故障，能量与多尺度熵都存在相同的缺陷，即对特征相似的时间序列区分能力欠佳。考虑到两者分别代表时间序列的动力学特性和能量波动这两方面特征，其易混淆的故障种类是不同的，将两者结合起来可以有效增加故障特征的区分度，定义MSEE为

EMSEE={EMSE1,…,EMSEτ,E}。

(17)

3 基于LMD和MSEE的滚动轴承复合故障特征提取方法

基于上述分析，将LMD和MSEE相结合，用于滚动轴承复合故障的特征提取，其具体流程如图1所示。

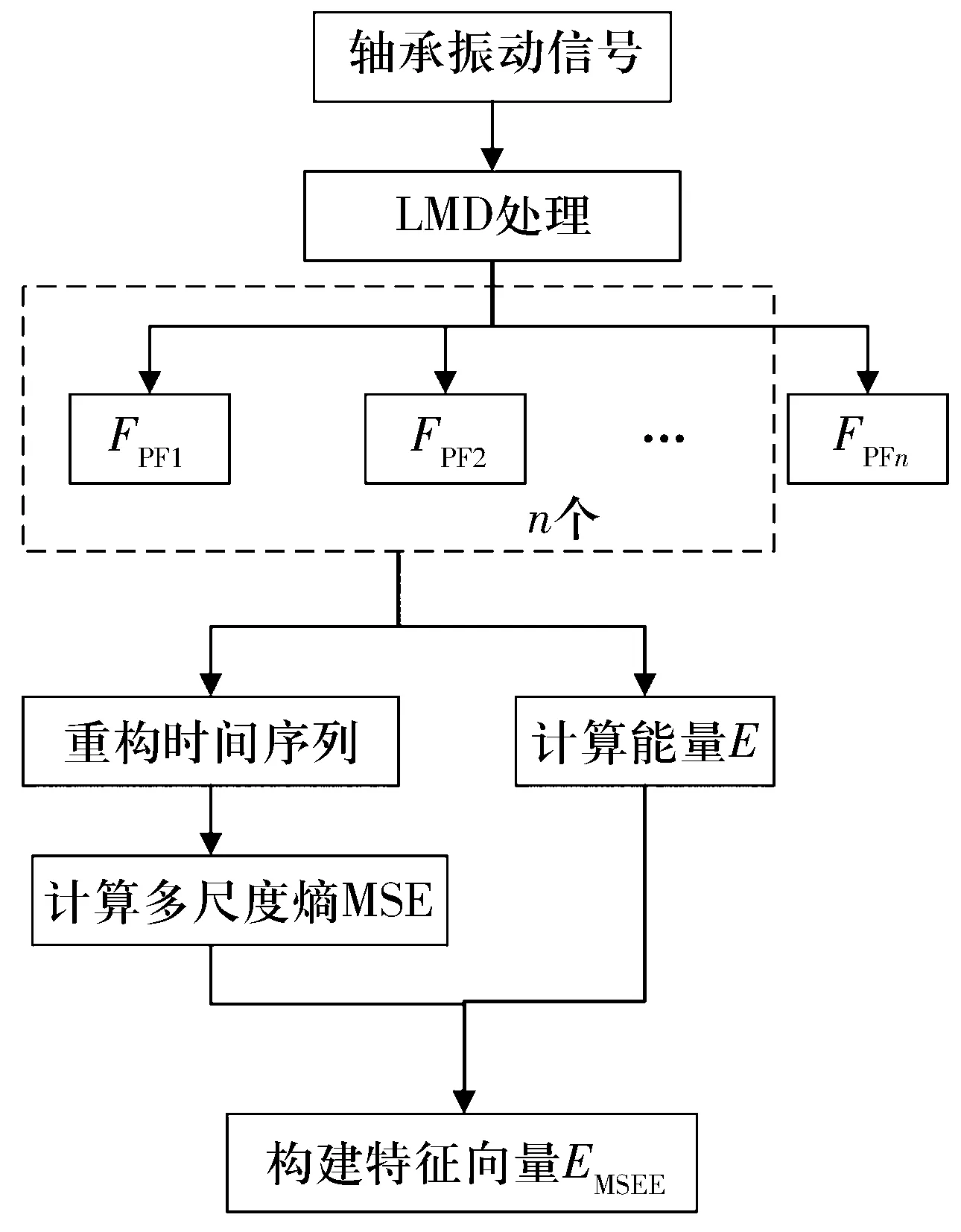
图1 基于LMD和MSEE的特征提取方法

基于LMD和MSEE的滚动轴承复合故障特征提取方法的优势在于从实际的角度出发，排除了噪声对结果的干扰，将轴承故障信号的序列规律性和能量分布作为区分不同故障的依据，极大增加了特征识别能力，对难以区分的复合故障信号有较好的特征提取效果。

4 试验分析

为验证LMD+MSEE方法的故障特征提取效果，选择如图2所示的机械故障模拟试验台进行试验，其能够通过更换故障轴承的方式采集轴承故障信号。

图2 机械故障模拟试验台

在轴承座上安装加速度传感器测量轴承振动信号，轴承型号为KR-12K，内径为19.05 mm，外径为46.99 mm，钢球数为 8，球径为7.87 mm，接触角为0。故障种类分为外圈故障、内圈故障、钢球故障、内圈+钢球故障、外圈+内圈故障和外圈+钢球故障。采样频率为2.56 kHz，旋转频率为30 Hz，采样点数取4 000。不同故障轴承在机械故障模拟试验台上的原始时间序列如图3所示。从图中可以看出，复合轴承故障的冲击信号呈现非周期性且幅值不等，仅从时域信号无法进行有效区分。

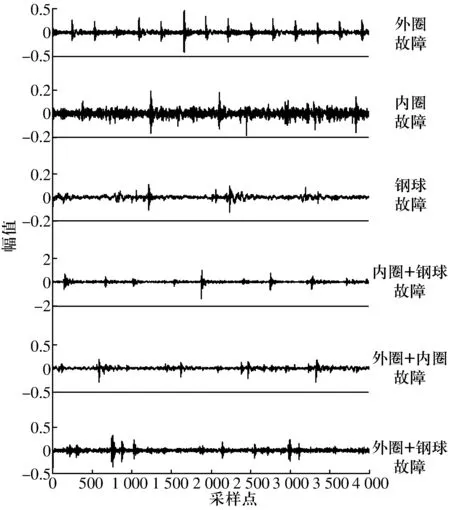
图3 轴承故障信号的时域信号图

按照上述方法首先对时域信号进行LMD处理，并计算各PF分量与原始信号的相关系数。由于篇幅有限，仅以内圈+钢球故障信号为例进行说明，故障信号经LMD处理后的6个PF分量如图4所示，各PF分量的相关系数见表1。

图4 内圈+钢球故障信号的LMD处理图

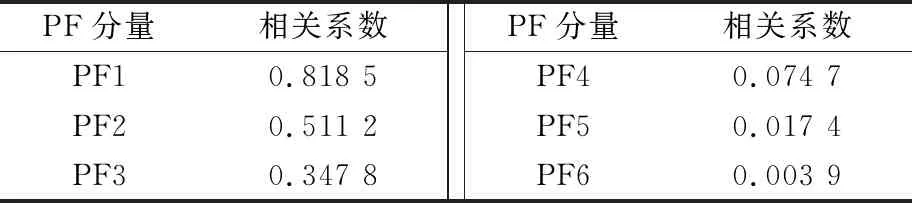
表1 PF分量的相关系数

由表1中各PF分量与原始时间序列的相关系数可知，PF1呈现强相关性，PF2与PF3呈现中等相关性，其他PF分量呈现弱相关性，因此选用PF1，PF2和PF3构建新的时间序列，排除噪声的干扰。

分别计算正常信号和6种故障信号重构时间序列的MSE，其中尺度因子τ=20，相似容限r=0.15σ，嵌入维数m=2，各信号的MSE与尺度因子τ之间的对应关系如图5所示。

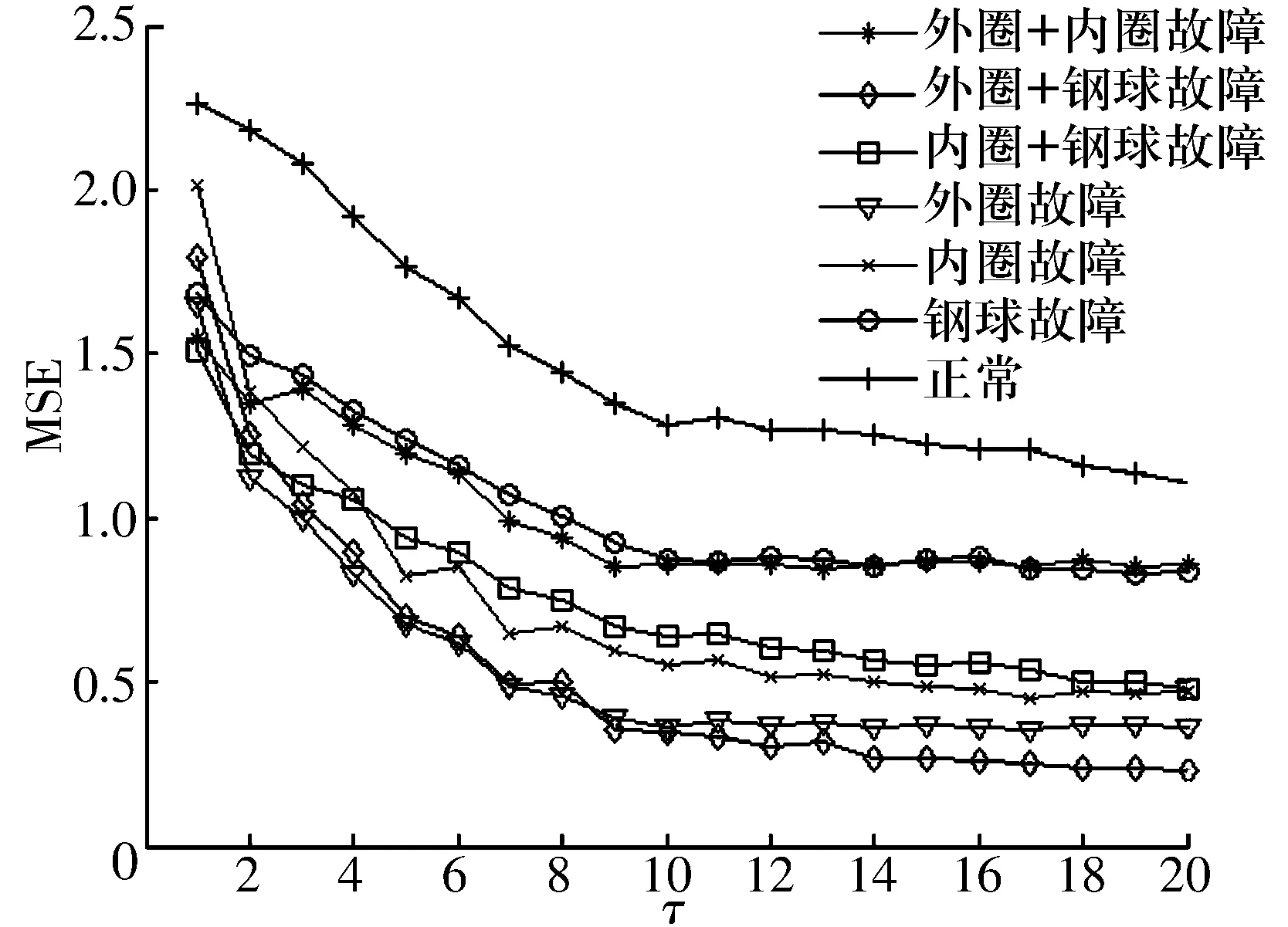
图5 轴承正常与故障状态下的MSE

从图5可以看出：

1)正常轴承的信号没有周期特征，因此其MSE大于故障信号，符合理论分析。

2)单一故障的MSE之间的差别十分明显，仅钢球故障和内圈故障的MSE在前2个尺度有交叠，整体区别性较大，说明MSE在单一轴承故障中有较好的特征提取效果。

3)一旦加入复合故障，MSE之间的区别就不再明显。在前2个尺度中，各故障的MSE相互交叠，很难区分；随着尺度因子增加，各故障MSE的差距开始加大，但仍存在混淆情况；当尺度因子τ处于2～10时，外圈故障与外圈+钢球故障的MSE较为接近，存在交叠的部分，难以区分；当尺度因子τ处于10～20时，钢球故障与外圈+内圈故障的MSE比较相似，容易混淆。

综上分析可知，在整个尺度域内，MSE不能满足提取轴承复合故障信号特征的需求。

当轴承处于故障状态时，由于信号中的能量也会产生波动，可以将能量作为特征提取的指标。LMD处理后各PF分量的能量如图6所示，由于正常信号只能分解到第5个PF分量，因此只给出了前5个PF分量的能量柱状图。在前3个PF分量上，信号的能量较为明显，符合表1中各PF分量的相关性。其中，在PF1分量上，内圈故障与外圈+内圈故障的能量相近；在PF2分量上，外圈故障与外圈+内圈故障的能量相近；在PF3分量上，内圈故障与钢球故障的能量相近。因此，能量也不能满足提取轴承复合故障信号特征的需求。

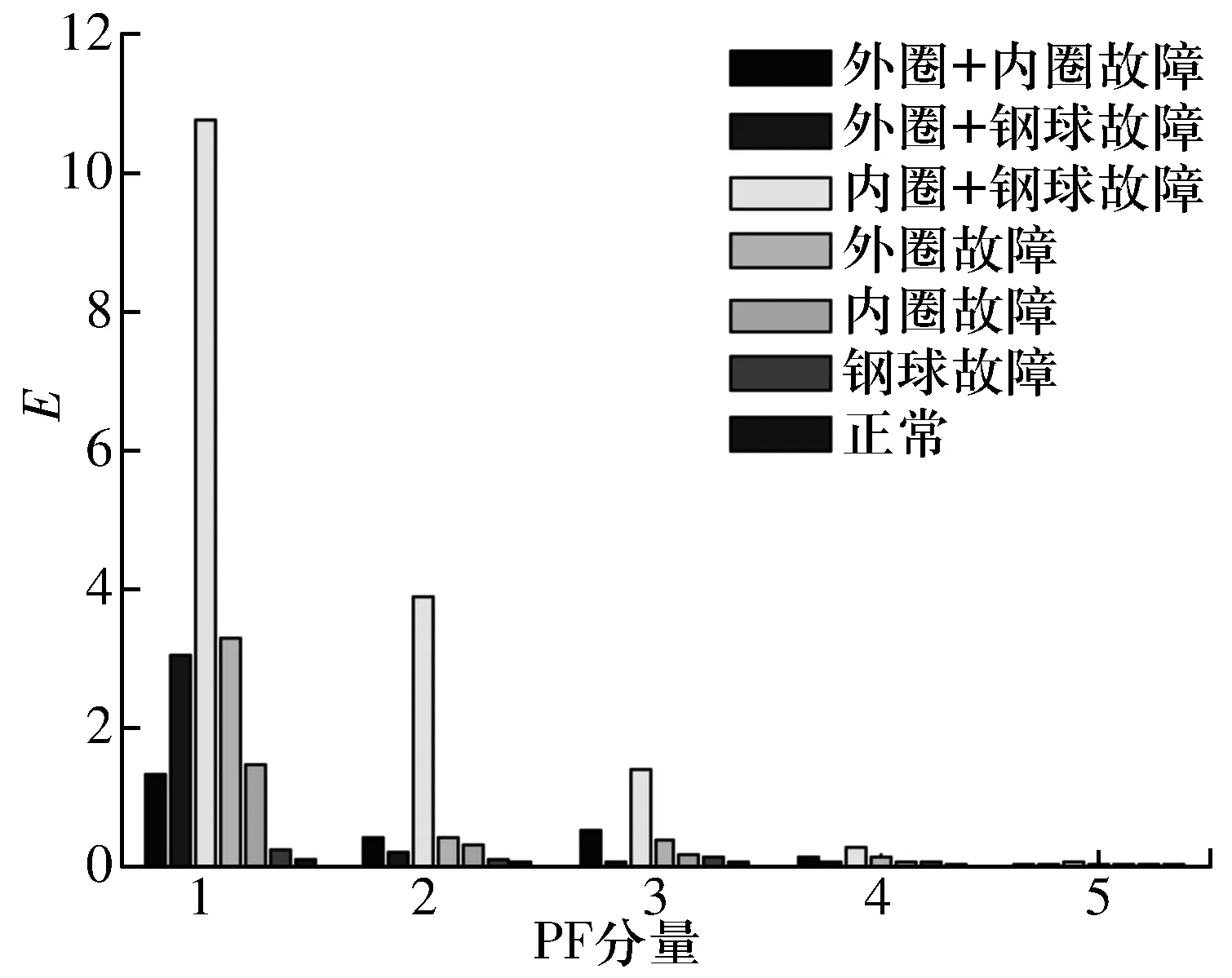
图6 轴承正常与故障状态下的PF能量

结合图5、图6分析可以发现，尽管各故障的MSE和能量都存在易混淆的情况，但混淆的故障种类有所不同，因此，需要将MSE与能量结合起来共同构建特征向量，增加故障特征的区分度，满足轴承复合故障信号特征提取的需求。

为进一步验证LMD+MSEE特征提取方法的优越性，采用最小二乘支持向量机(LS-SVM)作为分类器对特征向量进行模式识别，其中，核函数选择高斯核函数(RBF)。每种故障均选取100组振动信号，20组作为训练样本，剩下80组作为测试样本，其中每组振动信号有4 000个采样点。由于试验包含6种故障状态和1种正常状态，因此需要构造6个LS-SVM分类器，分别对应内圈故障、外圈故障、钢球故障、内圈+钢球故障、外圈+钢球故障和外圈+内圈故障，余下的则是正常信号。输入的特征向量分别采用MSE、能量和MSEE，并将输出的故障诊断结果进行对比，分类结果如图7所示，故障诊断率见表2。

从图7可以看出:当多尺度熵作为特征向量时，第3类故障与第6类故障的误报率较高，分别对应钢球故障和外圈+内圈故障；当能量作为特征向量时，第1类故障与第6类故障的误报率较高，分别对应内圈故障和外圈+内圈故障；当多尺度熵能量作为特征向量时，故障的误报情况得到了有效改善，没有十分明显的误报。由表2可知，与单独采用多尺度熵或者能量作为特征向量相比，采用多尺度熵能量的误报率分别降低了3.125%和3.75%，漏报率分别降低了5.21%和7.54%，故障诊断的正确率提升了8.33%和11.29%，充分验证了LMD+MSEE特征提取方法的优越性。

图7 LS-SVM的故障分类结果

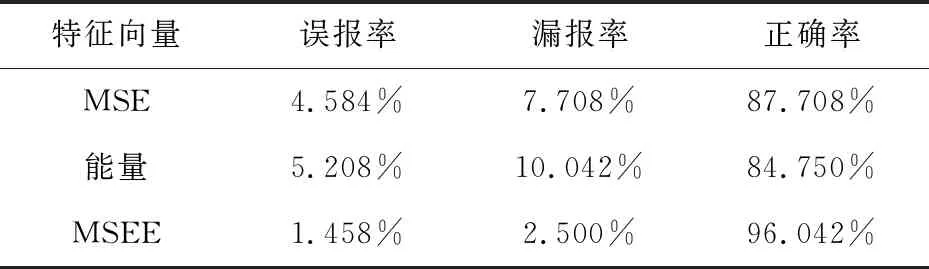
表2 LS-SVM的故障诊断率

5 结束语

提出了基于LMD和MSEE的滚动轴承复合故障特征提取方法，其可以抑制噪声的干扰，突出信号的主要成分，并增加特征向量的区分度，全面表征故障信号的特点，使特征更加明显，从而降低误报率、漏报率，在滚动轴承复合故障诊断中具有良好的应用效果。值得注意的是，该方法属于有监督的故障特征提取方法，即有已知类别的样本数据，对于未知样本类别的适用性，还需要进一步深入的研究。