基于复杂性测度的轴承振动状态监控

韦祥，李本威，吴易明

(1.海军航空大学 航空基础学院，山东 烟台 264001；2.洛阳轴承研究所有限公司, 河南 洛阳 471039)

轴承振动状态监控是保证旋转机械正常运行的重要手段，其监控方法应具备对状态变化的敏感性以及发现早期故障并预警的能力。由于结构的复杂性，材料的非线性本构关系，以及间隙、摩擦、润滑、弹性变形等非线性因素的影响，整个轴承系统具有非常复杂的非线性动力学行为[1]。建立准确的动力学方程并对其响应进行求解，从理论角度对系统的非线性振动特性进行研究困难重重。

目前，对轴承振动特性的研究以振动信号分析为主，普遍采用时域、频域振动总量作为振动状态监控的参数[2]。此类方法的监控信息过于单一，一些早期故障,甚至故障发展至一定程度后，仍不能通过振动总量反映，而且轴承运动稳定性与振动总量之间没有必然的映射关系。传统的频谱分析、伪相图等状态监测方法相比振动总量可以揭示更多的信息，但也只能在事后做出初步、定性的判断[3-4]。

随着非线性动力学的发展，最大Lynapunov指数[5]、分形维数[6]、熵等非线性动力学指数逐渐用于机械状态监控和故障诊断。利用响应时域波形“规则程度(或称复杂度)”和系统动力学结构、运行状态稳定性之间的关系实现不同故障种类、故障程度的特征提取是一种可行的方法。结合上述理论，提出了一种基于复杂性测度的轴承振动状态监测方法，以Lempel-Ziv复杂度(LZC)[7]和近似熵(ApEn)[8]作为信号复杂性测度的参量，以实现轴承早期微弱故障的预警。

1 复杂性测度

1.1 LZC

LZC可以度量类随机有限长度序列的复杂性，其利用序列本身具有子串数量的多少定义序列的复杂度，序列具有子串的个数越多，复杂度越高。但初始LZC二值粗粒化导致表征精度不高，因此提出了多值粗粒化[9]的方法。

1.1.1 将时间序列转化为符号序列。

设原时间序列为{x1,x2,…,xn}，求出该序列的最大值xmax和最小值xmin，设l为序列粗粒化的段数(当l=2时为经典二值粗粒化方法)，令d=(xmax-xmin)/l。对分割的区间进行符号化处理，数据落入该区间则被标记为该符号，其原理如图1所示，可以表示为

图1 多分段符号化方法原理

(1)

式中：{a(j)|j=1,2,…,l}为字符集。

从图1可以看出，多分段符号化方法在将时间序列转化为符号序列的过程中会丢失原始信号的细节信息，例如图中第3至第7个点在时间序列中的幅值明显不同，而符号序列均用1表示，抹平了序列的细节。原理上讲，分段数越多，信息量损失越小，表征越精确。不同分段数符号序列重构Mexihat函数的对比情况如图2所示(为便于图示，曲线进行了归一化处理)。分段数l=2时，只保留了Mexihat函数的大致形貌，信息损失较多，当l=50时基本较好地还原了Mexihat函数。对于l的选取，l越大，精度越高，计算效率也越低，工程应用时应根据具体需求选取。

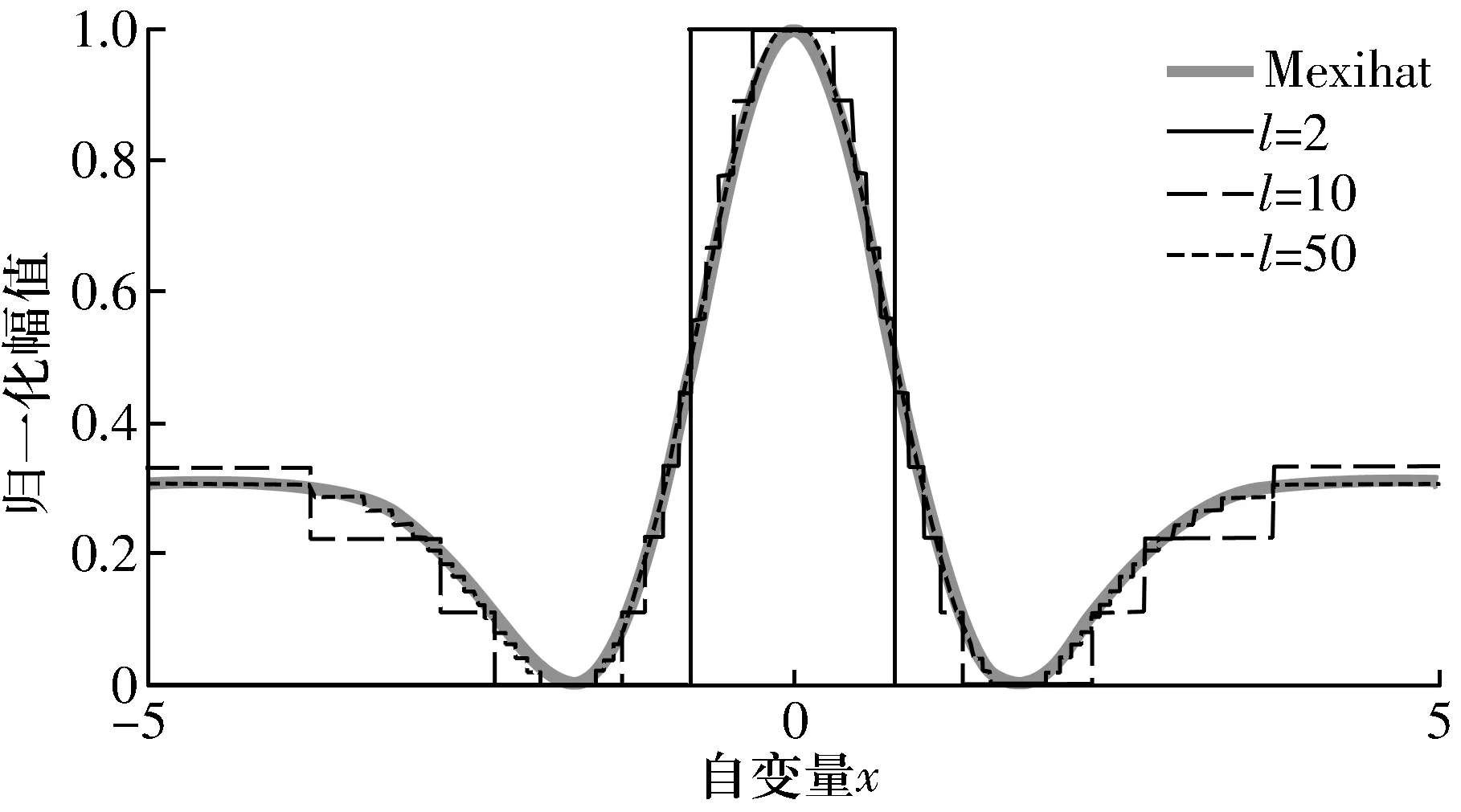
图2 不同分段数符号序列重构原信号

符号序列S=s1s2…sn的LZC计算过程如下：

1)S,Q分别代表2个字符串,SQ表示将S,Q相加组成的总字符串,SQP表示将SQ中最后一个字符删去所得的字符串。令V(SQP)表示SQP中所有不同子串的集合。

2)对于具体的符号序列，假定S=s1s2…sr,Q=sr+1,其中r+1=n。若Q∈V(SQP),则表示sr+1是S=s1s2…sr字符串的子串,此时S不变,将Q更新为Q=sr+1sr+2,再判断Q是否属于V(SQP)。此过程中,由于S不变但Q得到了更新,因此SQP也随之更新,如此反复进行,直到Q∉V(SQP)时中止。

3)设此时Q=sr+1sr+2…sr+i,即表明sr+1sr+2…sr+i不是s1s2…srsr+1sr+2…sr+i-1的子串。然后将上述Q组合到S中,使S更新为S=s1s2…srsr+1sr+2…sr+i,此时Q=sr+i+1。

4)重复以上步骤,直到Q取到最后一位为止。这样就将S分为了C(n)个不同的子串，C(n)即为该序列的复杂度。

1.2 ApEn

ApEn反映了时间序列在模式上的自相似程度以及维数变化时产生新模式的可能性。ApEn值越大，说明产生新模式的概率越大，序列越复杂，系统可预测性越差。ApEn给出新模式发生率随维数增减的情况，从而反映数据在结构上的复杂性。其计算方法如下：

1)对时间序列{U(i),i=1,2,…,n}进行相空间重构，重构维数为m，据此构造一组维数为m的新向量X(1),X(2),…,X(N-m+1)，其中X(i)={u(i),u(i+1),…,u(i+m-1)}，i=1,2,…,N-m+1。

2)计算任意向量X(i)与其余向量X(j)之间的相对欧式距离d[X(i),X(j)]。

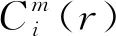
6)近似熵的估计值定义为

ApEn(m,r)=Φm(r)-Φm+1(r),

(2)

ApEn的取值与m和r有关，r=(0.1～0.2)σ，σ为原始数据的标准偏差，m取值范围通常为[2，5][8]。具体应用中参数的选取具有一定主观性，经过大量计算，虽然取值不同导致结果的数值有一定差异，但这种差异对于动力学结构的表征影响并不显著。

2 复杂性测度系统稳定性的定量判定

通过复杂性测度实现轴承振动状态监控，首要问题是验证ApEn和多值粗粒化LZC对系统运动稳定性的定量度量能力。相轨迹能够反映系统稳定性与运动模式的相关信息，研究动力系统的行为归结为在相空间中研究轨线的行为。利用目前研究较为成熟的Duffing系统为对象，研究复杂性测度与稳定周期运动和混沌运动的定量关系。

一个典型受迫Duffing系统的动力学方程为[11-13]

(3)

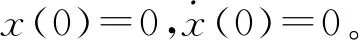
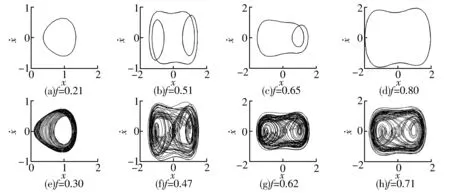
图3 Duffing方程典型状态下的相轨迹

图4 Duffing方程典型状态下的时域图

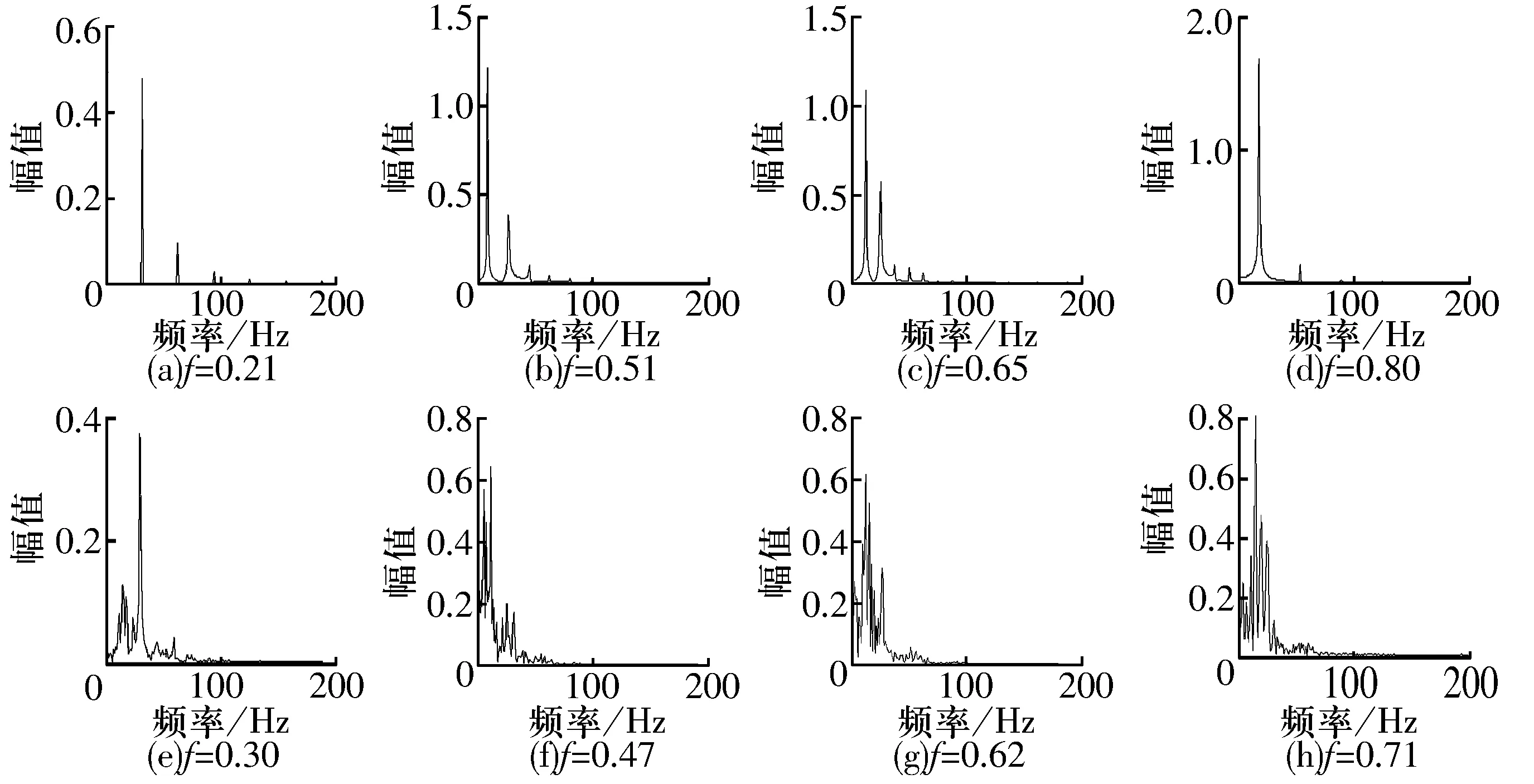
图5 Duffing方程典型状态下的频域图

从图中可以看出，系统运动状态复杂程度可通过相轨线及时、频域信号综合反映。具体表现为：1)系统处于稳定周期运动时，时域信号波形显示出周期性；f为0.21和0.80时，时域信号为类正弦信号，频域信号以基频为主，具有少量的谐波分量；f为0.51和0.65时，系统表现出时域信号具有周期性质的不规则波形，频域信号以基频为主，多阶谐波共存的情况。2)系统处于混沌状态时，系统表现出复杂的动力学行为，时域信号表现出高度不规则性，频域信号出现大量的谐波和次谐波;高阶频和次谐波的出现说明系统具有更加丰富的运动情况，信号中也包含更多的信息，即复杂度更高。

综上分析可知，振动信号波形不规则程度与相轨线复杂性、频谱复杂性成正相关。计算不同激励条件下Duffing方程的复杂度时，选取Runge-Kutta法求解稳定后的3 000个数据点进行复杂度计算，其中计算ApEn时m=5，r=0.15σ，计算Lempel-Ziv时l=50。LZC和ApEn对于Duffing系统典型状态下运动模式的复杂性度量情况见表1。由表可知，系统处于周期状态时复杂度较低，处于混沌态时复杂度较高。多值粗粒化LZC和ApEn对Duffing系统周期稳定性和混沌运动有着精确的表征和良好的区分度。

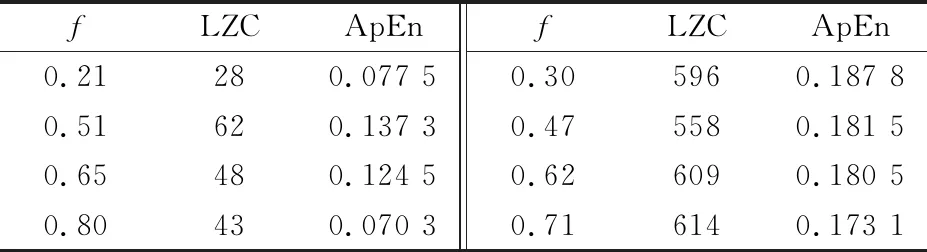
表1 Duffing方程典型状态下的复杂度

为进一步验证LZC和ApEn动力学结构表征的精确性，以Logistic映射为对象，验证复杂性测度对Logistic映射稳定不动点→不稳定不动点→周期→混沌这4个不同的演化阶段的表征情况。

Logistic映射方程为

xn+1=axn(1-xn)，

(4)

式中：3.5≤a≤4.0；步长为0.001；n=3 000。

Logistic映射分叉图，Lyapunov指数的理论值，LZC，ApEn如图6所示。从图中可以看出，LZC，ApEn与Lyapunov指数对Logistic映射周期不动点窗口位置及宽度度量结果完全相同，在整个区间内与Lyapunov指数保持高度相似的变化规律。Logistic处于周期不动点窗口时复杂性测度数值较低，Logistic分叉到混沌阶段复杂性测度数值较高，符合Logistic映射的动力学结构变化规律。说明LZC和ApEn是一种精确、可靠的动力学结构表征参量，对动力学结构变化敏感，可用于机械系统的状态监控。

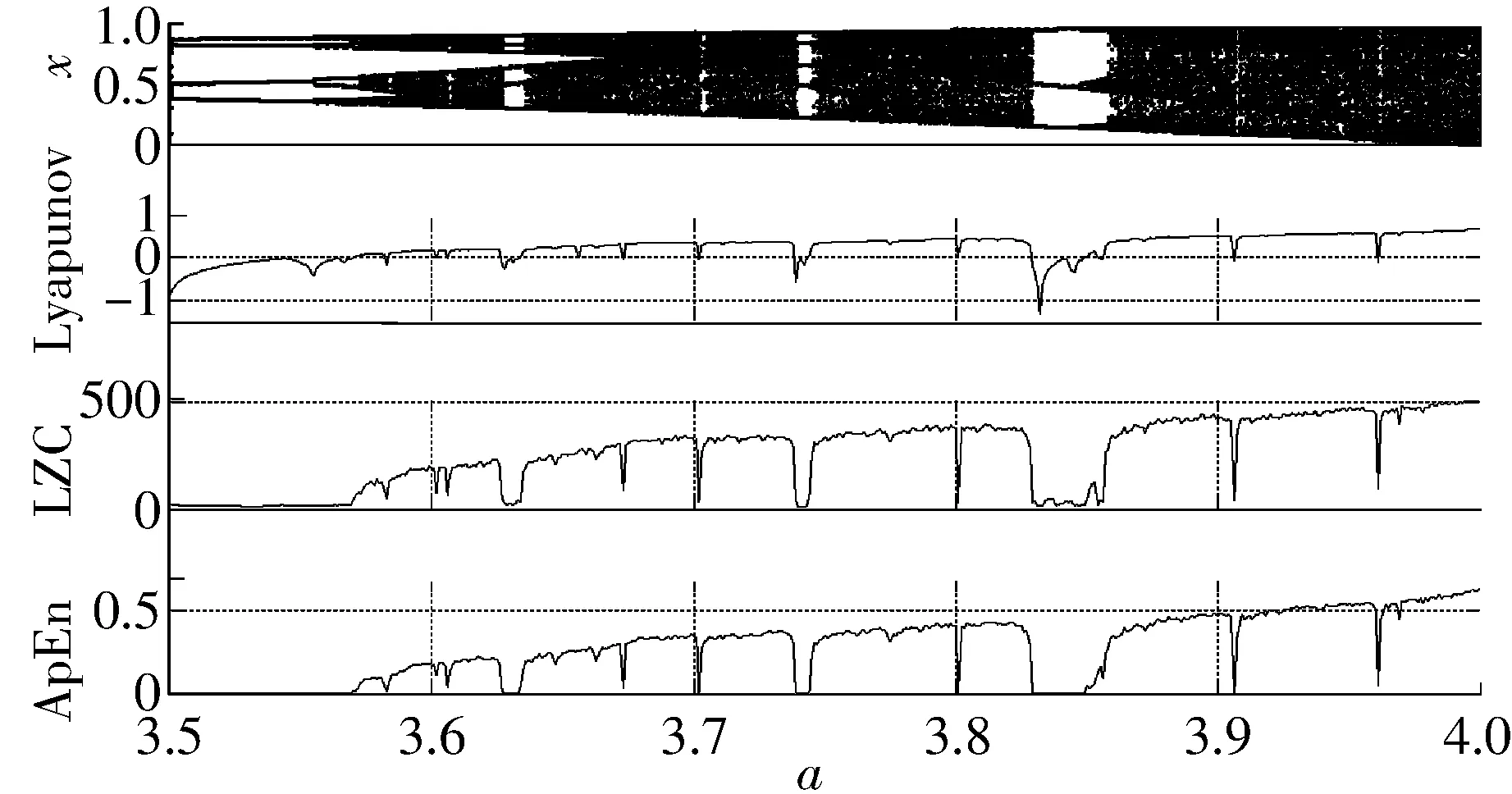
图6 Logistic映射动力学结构表征

3 复杂性测度的早期故障监测

轴承故障初期，由于损伤很小(磨损、裂纹等)，产生的故障信号不太强烈，在振幅和频域上表征不明显，现有的振动监控手段难以实现早期预警。从动力学角度分析，当轴承处于某一稳定状态时，信号包含的信息量是一定的。当轴承某一部件产生故障时，导致信息量和内在动力学结构的变化，因此通过检测内在动力学结构的变化即可对早期故障进行检测。

采用美国智能维数系统中心(IMS)的轴承疲劳试验数据[14-15]进一步研究复杂性测度的早期故障预警能力。试验台结构如图7所示，试验轴承为ZA-2115型双列滚子轴承，试验转速为2 000 r/min，通过弹簧装置加载26.67 kN的径向载荷，采样频率20 kHz，每隔10 min采集一次，采样点数为20 480个。试验从2月12日11:16:18运行至2月19日06:22:39，共采集984个文件数据。从轴承1的每个文件中选取3 000个点进行复杂度计算，ApEn中m=4，Lempel-Ziv中l=500，归一化的复杂度和实测信号如图8所示，为便于图示，数据进行了y轴平移处理。

图7 试验台结构示意图

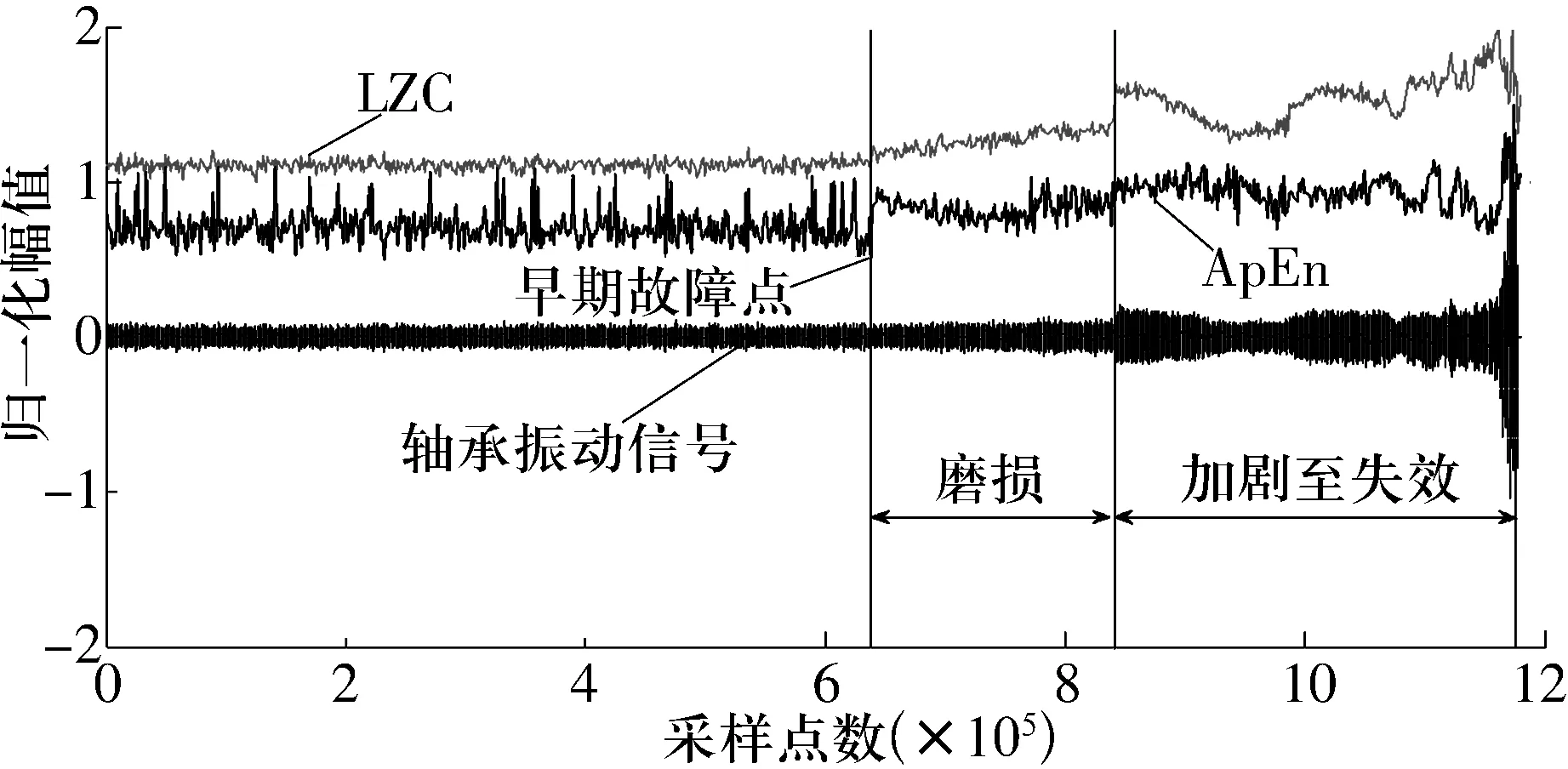
图8 轴承早期故障检测

从图中可以看出，ApEn和LZC在测量的第533个文件处检测到状态突变，并在第703个文件检测到了故障明显加剧。之后故障程度加深，振幅明显加大，轴承明显进入加速失效阶段，最终造成疲劳失效(图9)。

图9 轴承拆解后的外圈故障

4 结束语

经研究发现，直接度量信号波形复杂度可以从动力学角度实现轴承运动稳定性和早期故障的监测。Duffing系统复杂性度量的结果表明，多值粗粒化LZC和ApEn可实现周期信号和混沌信号的定量判别，可定量判定系统处于稳定状态还是非稳定状态。通过实测轴承振动信号进行早期微弱故障预警，试验结果说明ApEn和LZC可对动力学结构突变进行检测，是一种有效的轴承早期微弱故障预警手段。由于轴承振动信号超高采样频率导致大量数据处理的负担，如何提高动力学参数计算效率，以实现动力学参数对轴承实时状态监控是后续研究的重要方向。