船用燃机低压转子-轴承系统非线性动力学分析
2019-07-22李默刘永葆王强
李默,刘永葆,王强,b
(海军工程大学 a.动力工程学院;b.兵器工程学院,武汉 430033)
滚动轴承因摩擦因数小,质量轻,易于安装和冷却等优点,广泛应用于船用燃气轮机和航空发动机等转子系统,为转子系统提供良好的稳定支承。但轴承变刚度振动、非线性Hertz恢复力、径向游隙等非线性因素会引发转子系统的非线性动力学行为。
国内外对转子-轴承系统的非线性动力学特性做了大量研究。文献[1]考虑轴承径向游隙、变刚度频率等多个非线性因素,分析了转速对转子-轴承系统的非线性动力学特性的影响;文献[2]建立了两自由度转子-轴承系统,分析了系统阻尼变化对系统分岔、混沌的影响;文献[3]建立了转子-轴承系统动力学模型,结合Poincaré 映射图等进行了转子系统非线性特性分析;文献[4]考虑轴承波纹度等系统的非线性因素,分析了波纹度频率对系统振动的影响;文献[5]分析了不同转速下转子-轴承系统的分岔、混沌等非线性动力学特性;文献[6]考虑轴承的接触非线性和游隙非线性建立了偏置转子系统动力学模型,分析了径向游隙对偏置转子系统的非线性动力学影响;文献[7]建立了三自由度对称支承的转子-轴承系统动力学模型,分析了径向游隙对系统振动的影响;文献[8]建立了单自由度刚性转子非线性动力学模型,分析了径向游隙对系统非线性动力学的影响;文献[9]建立单自由度转子-轴承系统,分析轴承变刚度振动和强迫振动耦合振动对转子系统非线性动力学特性的影响;文献[10]建立单跨转子系统动力学模型,分析了转速、挤压油膜间隙对系统非线性动力学特性的影响;文献[11]建立转子-轴承系统有限元模型,分析了结构参数对连续质量的转子系统非线性动力学特性的影响;文献[12]建立了陀螺仪转子-轴承系统非线性动力学模型,分析了转子-轴承系统的阻尼刚度对系统非线性动力学特性的影响;文献[13-15]建立了偏置转子系统非线性动力学模型,分析了偏置距离和径向游隙对转子系统非线性动力学特性的影响;文献[16-17]建立了四支承双跨转子系统动力学模型,分析了轴承支承下的故障转子非线性动力学特性;文献[18-19]建立了三支承双跨转子系统动力学模型,分析了滑动轴承支承下故障转子系统的非线性动力学特性。
上述研究对转子-轴承系统进行了非线性动力学分析,但仅针对简单的单跨单盘双支承转子-轴承系统,结构参数单一,未根据实际转子-轴承结构进行建模。鉴于此,以某船用燃气轮机转子-轴承系统为例,建立1套深沟球轴承和2套圆柱滚子轴承的三支承双跨形式转子-轴承系统,分析支承轴承转速和径向游隙对系统非线性特性的影响。
1 滚动轴承建模
为便于对转子-轴承系统进行非线性动力学分析,做如下假设:1)轴与轴承内圈刚性连接;2)轴承座与轴承外圈刚性连接;3)滚动体在滚道内自由滚动,不产生滑动。滚动轴承简化模型如图1所示,图中:O1为轴承不受载时的轴质心;O2为轴承受载后的轴质心;Ri为内圈半径;Re为外圈半径;Gr为径向游隙;j表示第j个滚动体;θj为第j个滚动体位置角。
根据几何关系可得
(1)
式中:Z为滚动体数量;t为运动时间。

图1 滚动轴承简化模型
第j个滚动体接触变形量为
χj=xcosθj+ysinθj-Gr,
(2)
式中:x,y为受载后轴质心坐标。
接触只能产生正向接触压力,当χj<0时,不会产生压力,仅χj>0时才会有压力,引入Heaviside函数,即
(3)
根据Hertz接触理论得到轴承恢复力为
(4)
式中:Fbx,Fby分别为轴承在x,y方向的恢复力;Kb为接触刚度;Fj为第j个滚动体所受载荷;n为载荷-变形指数,对于深沟球轴承,n=3/2,对于圆柱滚子轴承,n=10/9。
2 转子-轴承系统建模
根据某船用燃气轮机低压转子-轴承系统的实际支承形式,将转子系统简化为三支承双跨的三盘转子系统,如图2所示。图中:O为坐标原点;Ob1,Ob2,Ob3分别为轴承1,2,3的形心;Op1,Op2,Op3分别为盘1,2,3的形心;Oc1,Oc2,Oc2分别盘1,2,3的质心;e1,e2,e3分别为盘1,2,3的偏心距。A段模拟压气机段,由2个刚性盘模拟,分别位于压气机段的三等分处;B段模拟涡轮段,由一个刚性盘模拟,位于涡轮段中点:整个转子系统由3套轴承支承(轴承1为深沟球轴承,轴承2,3为圆柱滚子轴承)。模型考虑转子在轴承和圆盘处的集中质量,转子与轴承之间采用无质量弹性轴,忽略转子扭转振动和轴向振动,仅研究横向振动,每个集中质量只考虑x,y这2个方向的自由度。

图2 转子-轴承系统简化模型
假设3个盘偏心距相同,由于主要研究轴承对系统非线性响应的影响,假设压气机段和涡轮段转子结构、材料相同,根据平面梁结构关系得到轴段的刚度关系为:k1=k3=k/2,k2=2k,k4=k5=k,k=2.5×107N/m。根据Lagrange运动方程和转子动力学理论得到系统非线性动力学微分方程组为
(5)
M=diag(mb1,mp1,mp2,mb2,mp3,mb3),
C=diag(cb1,cp1,cp2,cb2,cp3,cb3),
K=
Fbx=(Fbx,0,0,Fmx,0,Frx)T,
Fby=(Fby,0,0,Fmy,0,Fry)T,
X=(xb1,xp1,xp2,xb2,xp3,xb3)T,
Y=(yb1,yp1,yp2,yb2,yp3,yb3)T,
Fex=(0,mp1e1ω2cos(ωt),mp2e2ω2cos(ωt),
0,mp3e3ω2cos(ωt),0)T,
Fey=(0,mp1e1ω2sin(ωt),mp2e2ω2sin(ωt),
0,mp3e3ω2sin(ωt),0)T,
式中:M为系统刚度矩阵;C为系统阻尼矩阵;K为系统刚度矩阵;Fbx,Fby为轴承恢复力矩阵;Fex,Fey为转子不平衡力矩阵;g为重力加速度;mb1,mb2,mb3分别为转子在轴承1,2,3处的集中质量;mp1,mp2,mp3分别为转子在盘1,2,3处的集中质量;cb1,cb2,cb3分别为转子在轴承1,2,3处的阻尼;cp1,cp2,cp3分别为转子在盘1,2,3处的阻尼;Flx,Fmx,Frx为轴承1,2,3恢复力的水平分量;Fly,Fmy,Fry为轴承1,2,3恢复力的垂直分量;ω为角速度;xb1,xb2,xb3分别为轴承1,2,3的水平位移;xp1,xp2,xp3分别为盘1,2,3的水平位移;yb1,yb2,yb3分别为轴承1,2,3的垂直位移;yp1,yp2,yp3分别为盘1, 2,3的垂直位移。
引入量纲一化参数
(6)
式中:γ是与轴承径向游隙相当的一个长度量,数值选择根据数值计算方便。
对(5)式进行量纲一化处理可得
(7)
3 系统非线性动力学分析
轴承主要结构参数见表1,转子参数为:mb1=1.2 kg,mb2=1.2 kg,mb3=1.2 kg,mp1=2.09 kg,mp2=11.00 kg,mp3=6.00 kg,cb1=2 200 N·s/m,cb2=2 200 N·s/m,cb3=2 200 N·s/m,cp1=1 050 N·s/m,cp2=1 050 N·s/m,cp3=1 050 N·s/m,k=2.5×107N/m,e1=e2=e3=10 μm。微分方程组具有强非线性,故采用四阶Runge-Kutta法求解。变刚度频率fvc=frRi/(Ri+Re)(fr为轴旋转频率)。

表1 轴承主要结构参数
3.1 转速对系统非线性动力学特性的影响
随转速逐渐增大,旋转机械运动状态发生复杂变化。以转速n为变量,分析盘1水平位移的分岔非线性特性,结果如图3所示。由图3可知:随转速增大,盘1经历了拟周期、单周期、拟周期、周期二、周期四、周期二和单周期运动过程,说明系统具有复杂的非线性特性。
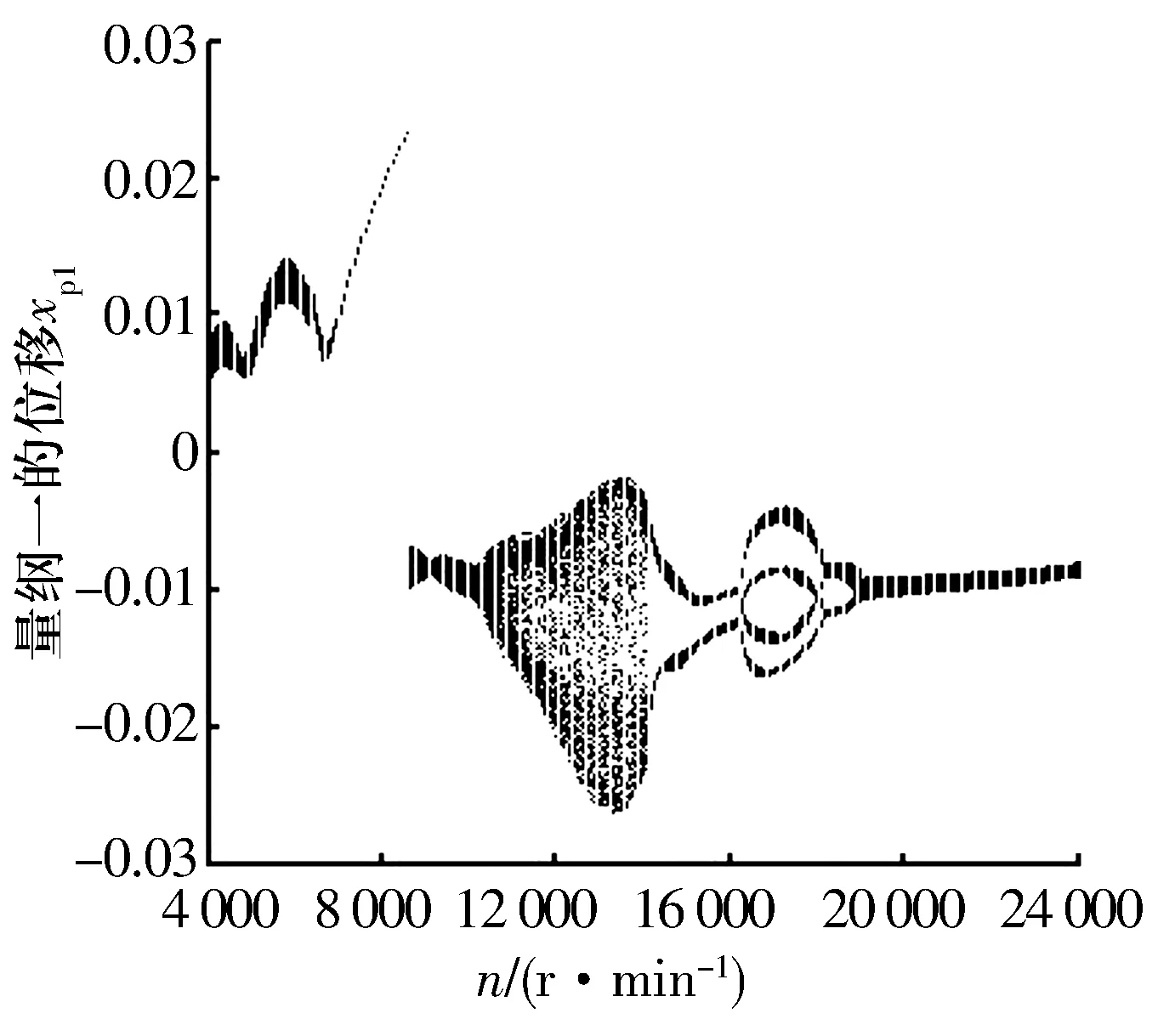
图3 盘1水平位移随转速变化的分岔图
在n=1 432 r/min时盘1的频谱图如图4所示(频率比λ为特征频率与旋转频率的比值),由图可知:系统有3个激振频率,1个转速激励频率和2个轴承变刚度频率。在fr,fvc1(轴承1变刚度频率),fvc2(轴承2,3变刚度频率)处出现峰值,且变刚度频率幅值大于旋转频率幅值,系统振动频率以轴承变刚度频率为主。分析结果与文献[20]一致。

图4 在n=1 432 r/min时盘1的频谱图
盘1水平位移随转速变化的三维谱图如图5所示,由图可知:随转速增大,盘1变刚度频率幅值逐渐减小,旋转频率幅值逐渐增大,不平衡激励为盘1的主要激励。当转速远小于临界转速(8 000 r/min)时,盘1变刚度频率和旋转频率的作用差别不大,轴承变刚度频率幅值与旋转频率幅值接近,且频率不可相约,故盘1表现为拟周期运动。

图5 盘1水平位移随转速变化的三维谱图
不同转速下盘1的庞加莱图和频谱图如图6所示,由图可知:1)n=5 254 r/min时,庞加莱图为一个封闭曲线,频谱图有多个不可相约的主要峰值;2)n=9 745 r/min时,庞加莱图为一个点,频谱图上主要是旋转频率及其倍频;3)n=14 426 r/min时,庞加莱图为一个不规则的封闭曲线,频谱图上出现较多的低倍频。

图6 盘1的庞加莱图(左)和频谱图(右)
随转速增加,不平衡激励及其分频越来越明显,盘1逐渐出现分岔运动。更高的转速下,盘1的庞加莱图如图7所示,由图可知:在转速为18 535,20 636,22 356,24 936 r/min时庞加莱图分别为2个单点、4个单点、2个单点和1个单点,对应盘1的周期二、周期四、周期二和单周期运动。

图7 高转速下盘1的庞加莱图
3.2 径向游隙对系统非线性动力学特性的影响
3.2.1 3套轴承同时变化
转子-轴承系统非线性因素主要来自轴承恢复力,体现为轴承载荷-变形指数和恢复力分段性。根据Hertz接触理论,载荷-变形指数与轴承类型有关,恢复力分段性由径向游隙决定,与轴承结构参数有关。在此分析径向游隙同时变化对系统非线性动力学特性的影响。
3套轴承径向游隙相同,随径向游隙增大盘1水平位移的分岔图如图8所示,由图可知:随径向游隙增大,盘1经历了单周期、周期二、周期四和周期二运动。当径向游隙小于6.4 μm时,盘1进行单周期运动,此时径向游隙较小,轴承恢复力非线性比较弱,轴承恢复力对系统非线性运动影响较小;径向游隙为6.4~11.1 μm时,盘1进行周期二运动,径向游隙增大使盘1发生倍周期分岔;径向游隙为11.1~ 25.9 μm时,盘1进行周期四运动;最后进行周期二运动。
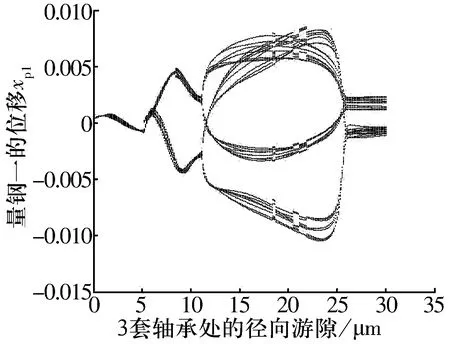
图8 随径向游隙增大盘1水平位移的分岔图
不同径向游隙时盘1水平位移的相图如图9所示,由图可知: 当径向游隙为5 μm,相图为一个封闭曲线;当径向游隙为8 μm,相图为2个封闭曲线;当径向游隙为20 μm时,相图为4个封闭曲线;当径向游隙为28 μm时,相图为2个封闭曲线。不同径向游隙时盘1的庞加莱图如图10所示,由图可知:当径向游隙为5 μm时,庞加莱图为孤立的点;当径向游隙为8 μm时,庞加莱图为2个孤立的点;当径向游隙为20 μm时,庞加莱图为4个孤立的点;当径向游隙为28 μm,庞加莱图又是2个孤立的点;分析结果与盘1的水平位移分岔图对应。

图9 不同径向游隙时盘1的相图

图10 不同径向游隙时盘1的庞加莱图
3.2.2 单套轴承径向游隙变化
在实际工作过程中,由于系统质量沿轴向分布不均或由于润滑不足等原因,滚动体与内、外滚道接触而磨损,会使轴承径向游隙发生较大的变化,偏离了原始设计值。根据某船用燃气轮机实际工况,涡轮处轴承工作在高温环境中时,轴承径向游隙变化较大,在此分析右端轴承(轴承3)径向游隙变化对系统非线性动力学特性的影响。
随轴承3径向游隙变化,盘1水平位移的分岔图如图11所示。由图可知:当径向游隙小于2.2 μm时,盘1进行单周期运动;当径向游隙超过2.2 μm时,盘1通过倍周期分岔进入周期二运动状态,且大范围游隙内盘1进行周期二运动。

图11 盘1水平位移随轴承3径向游隙变化的分岔图
轴承3不同径向游隙时盘1的相图和庞加莱截面图如图12所示,由图可知:1)径向游隙为2 μm时,盘1相图只有一个封闭的圆形,庞加莱图上只有一个孤立的单点,充分说明了此时盘1处于单周期运动状态;2)径向游隙为20 μm时,盘1的相图有2个互相交叉的封闭圆形,庞加莱图有2个孤立的点,说明此时盘1处于周期二运动状态。

图12 轴承3不同径向游隙时盘1的相图和庞加莱图
4 结论
以某船用燃气轮机为研究对象,建立了三支承双跨三盘滚动轴承支承动力学模型,分析了转速、径向游隙对转子-轴承系统非线性动力学特性的影响,得出以下结论:
1)随转速增大,轴承变刚度影响变弱,系统主要表现为转频的倍频和分频运动,出现拟周期、单周期、周期二、周期四等复杂非线性运动。
2)3套轴承径向游隙同时增大时,系统通过倍周期分岔途径运动,且轴承径向游隙越大,系统运动越复杂,当径向游隙超过一定范围,由于游隙过大,滚动体与内外圈接触不充分,系统表现为周期二运动。在轴承设计时,应根据转子系统工作环境温度、载荷等,控制轴承径向游隙小于6.4 μm,保证转子系统处于稳定的单周期运动状态。
3)由于转子-轴承系统右端轴承径向游隙增大,系统通过倍周期分岔途径由单周期过渡到周期二运动,该非线性特性可作为右端轴承径向游隙增大的判断依据,为轴承故障诊断提供理论依据。
