中大型圆柱滚子轴承柔性保持架动力学分析
2019-07-22龚岸琦姚廷强咸利国
龚岸琦,姚廷强,咸利国
(昆明理工大学 机电工程学院,昆明 650500)
圆柱滚子轴承滚子与滚道之间为线接触,其径向承载能力较大,既适用于承受重载荷与冲击载荷,也适用于高转速工况,广泛应用于重型旋转机械设备。通常情况下轴承所能承受的载荷以轴承运转过程中的疲劳寿命为依据,但圆柱滚子轴承轴向承载能力取决于挡边强度及滚子端面与套圈挡边之间滑动摩擦发热程度[1]。对处于高速或振动较大工况的中大型圆柱滚子轴承,由于保持架运动不稳定及滚子打滑[2],易引起滚子和套圈挡边、滚子和保持架兜孔以及保持架和套圈引导面之间接触表面的磨损和擦伤,从而引起轴承早期失效。故有必要对中大型圆柱滚子轴承保持架动力学特性进行分析。
国内外学者对保持架动力学特性做了大量研究。文献[2]建立了高速圆柱滚子轴承动力学微分方程对保持架的动力学特性进行分析;文献[3]基于拟动力学法和有限元法分析了圆柱滚子轴承静、动态载荷特性和保持架的径向平面运动轨迹;文献[4]基于拟静力学法分析了径向载荷、滚子数量等因素对保持架打滑率的影响;文献[5-6]建立了保持架涡动模型,分析了保持架涡动产生的极力;文献[7]对保持架的受力和磨损进行了分析;文献[8]基于拟动力学模型分析了保持架和滚子的打滑特性;文献[9]分析了轴承转速、载荷、游隙等对保持架质心运动轨迹的影响。
上述模型大多基于拟静力学或拟动力学进行理论分析,理论模型考虑并不全面。鉴于此,在考虑了滚子与套圈滚道、滚子与保持架兜孔及保持架与套圈引导面的动态接触关系的前提下,基于ADAMS建立圆柱滚子轴承柔性保持架动力学仿真模型,分析了不同转速和载荷下轴承的动态特性。
1 圆柱滚子轴承动力学模型
以圆柱滚子轴承NU1020ML为例分析,轴承内、外圈及滚子材料均为GCr15轴承钢,保持架为铜,其主要结构参数见表1,材料参数见表2。轴承外圈带挡边,内圈无挡边,引导方式为外圈引导,内圈旋转,外圈固定。

表1 主要结构参数

表2 材料参数
为了节约求解时间,在不影响轴承运动和内部应力的前提下建模时忽略滚子倒角的影响,建立的动力学仿真模型如图1所示。

图1 动力学仿真模型
1.1 基本假设
为简化计算,对高速滚子轴承的动力学模型做以下假设:
1)假设套圈和滚子为刚体,忽略结构弹性变形,仅考虑局部接触弹性变形。保持架为柔性体,同时考虑结构弹性变形和局部接触弹性变形;
2)根据实际工况,圆柱滚子轴承动力学模型中滚子和保持架均具有6个自由度,内圈具有5个自由度,仅约束内圈在z方向的移动,外圈固定;
3)保持架兜孔形状为矩形,轴承各零件的形心与质心重合;
4)轴承内部温度已知,忽略轴承内部润滑作用,考虑为干摩擦。
1.2 柔性保持架模型的建立
滚动轴承保持架动态性能对轴承的整体性能有重要影响[10]。考虑保持架的结构弹性变形和动态接触冲击,基于ADAMS/Flex模块建立了柔性保持架模型,并计算得出48阶模态,部分模态见表3,对应振型如图2所示。由于轴承全频段50~10 000 Hz[11],在取消前6阶刚性模态和其余超频模态之后,仿真并提取分析动态响应结果。通过仿真可知:保持架模态从开始在环平面内的弯曲振动慢慢转为保持架在圆周方向上的弯扭耦合振动。

表3 部分模态

图2 柔性保持架振型
2 圆柱滚子轴承接触力计算
当两零件表面之间发生接触时,会在接触位置产生接触力。ADAMS基于Hertz接触理论利用Impact函数提供的非线性等效弹簧阻尼模型作为两零件之间接触力的计算模型。接触力由两部分组成:1)两零件之间的相互切入而产生的弹性力;2)由于相对运动而产生的阻尼力[12]。两零件接触力可表示为
(1)
K=7.86×104l8/9,
式中:K为接触刚度[9];l为有效接触长度;δi为接触点的最大法向穿透深度;e为碰撞力指数,对于金属材料e取1.5;C为最大阻尼系数,一般取10~100 N·s/mm;Vi为接触点法向相对速度。
3 仿真分析
3.1 转速对轴承动态特性的影响
在径向载荷为15 kN(重载)的条件下,不同内圈转速下同一滚子与内圈滚道和外圈挡边接触力如图3所示,内圈滚道最大接触力及均方值见表4。由图3和表4可知:圆柱滚子轴承滚子与内圈滚道的接触力呈周期性变化,这说明载荷区和非载荷区循环变化。滚子与挡边接触频繁且非载荷区接触力幅值远大于载荷区幅值。随转速增加,滚子与滚道和挡边的接触力均增加。
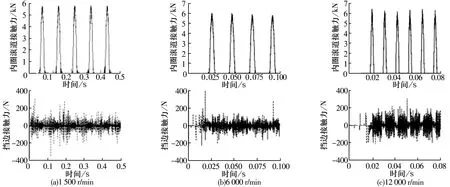
图3 不同转速下滚子与内圈滚道和外圈挡边的接触力

表4 不同转速下内圈滚道接触力最大值及均方值
在径向载荷为15 kN的条件下,不同内圈转速下保持架与套圈引导面的接触力如图4所示,均方根见表5。由图4和表5可知:保持架与套圈引导面的接触力受转速影响较大,并存在明显的载荷区和非载荷区循环变化规律,尤其是启动加速阶段存在较大的接触碰撞力。

图4 不同转速下保持架与套圈引导面的接触力

表5 不同转速下保持架与套圈引导面的接触力均方值
在径向载荷为15 kN的条件下,不同内圈转速下滚子自转速度如图5所示。由图5可知:滚子的自转速度存在明显的载荷区与非载荷区的骤变现象,滚子进入载荷区时自转速度趋于平稳,进入非载荷区时自转速度会发生骤降。随转速增加,滚子自转速度增加,波动幅值减小,滚子趋于平稳所需的时间减少。

图5 不同转速下滚子自转速度
在径向载荷为15 kN的条件下,不同内圈转速下保持架质心轨迹如图6所示。由图6可知:在转速较低的情况下,圆柱滚子轴承保持架质心在一个半圆区域涡动,但质心运动最后集中在一块狭小区域内;随转速增加,保持架质心涡动范围呈现出圆形轨迹。

图6 不同转速下保持架质心位移
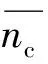

表6 不同转速下保持架转速及打滑率

图7 不同转速下的保持架转速
nc=[ne(1+γ)+ni(1-γ)]/2,
(2)
γ=Dwcosα/Dpw,
式中:ne为外圈转速;ni为内圈转速;Dw为滚子直径;Dpw为滚子组节圆直径;α为接触角。
轴承外圈固定,保持架打滑率S为
(3)

通过计算可得保持架理论转速及打滑率见表6。圆柱滚子轴承保持架转速随转速增大而增大,保持架打滑率随转速增加而降低,说明圆柱滚子轴承会随转速增加运行变得更稳定。
3.2 载荷对轴承动态特性的影响
在转速为12 000 r/min(高速)的条件下,不同径向载荷下同一滚子与内圈滚道和挡边的接触力如图8所示,内圈滚道接触力最大值及均方值见表7。由图8和表7可知,圆柱滚子轴承滚子与套圈滚道的接触力存在明显的载荷区和非载荷区的骤变现象,滚子与挡边接触频繁且非载荷区的接触力幅值远大于载荷区。随径向载荷增加,滚子与套圈滚道接触力不断增加,但滚子与挡边接触力并无明显变化规律。

表7 不同载荷下内圈滚道接触力最大值及均方值

图8 不同载荷下滚子与内圈滚道和外圈挡边的接触力
在转速为12 000 r/min的条件下,不同径向载荷下保持架与套圈引导面的接触力如图9所示,均方值见表8。由图9和表8可知:保持架与套圈引导面的接触力受径向载荷的影响较小,但仍存在明显的载荷区和非载荷区的骤变现象,尤其是启动加速阶段存在较大的接触碰撞力。

表8 不同载荷下保持架与套圈引导面的接触力均方值

图9 不同载荷下保持架与套圈引导面接触力
在转速为12 000 r/min的条件下,不同径向载荷下滚子自转速度如图10所示。由图10可知:滚子自转速度波动幅值较小,随径向载荷的增加,滚子自转速度趋于平稳所需的时间减少。

图10 不同载荷下滚子自转速度
在转速为12 000 r/min的条件下,不同径向载荷下保持架质心位移如图11所示。由图11可知:在轻载工况下保持架质心的运动轨迹呈半圆周涡动现象;随径向载荷增大,保持架质心涡动范围增大,且呈现出圆形轨迹。

图11 不同载荷下保持架质心位移
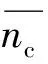

图12 不同载荷下保持架转速

表9 不同载荷下保持架转速和打滑率
4 结论
考虑滚子与套圈滚道、滚子与柔性保持架兜孔、柔性保持架与套圈引导面的动态接触关系建立圆柱滚子轴承刚柔耦合多体接触动力学仿真模型进行分析,得出以下结论:
1)滚子与内圈滚道的接触力随载荷或转速的增大而增大,滚子与挡边的接触力、保持架与套圈引导面间的接触力受转速影响较大,尤其是启动加速阶段存在较大的接触碰撞力;在高速和重载工况下,滚子与挡边的接触力存在明显的载荷区和非载荷区循环变化规律,且非载荷区幅值远大于载荷区。
2)转速较低时,滚子进入载荷区时自转速度趋于平稳,进入非载荷区时自转速度会发生骤降。随转速增加,保持架和滚子的转速波动幅值减小。
3)在低速重载或高速轻载工况下,保持架质心轨迹是部分圆轨迹;随转速或载荷增加,涡动范围呈现出圆轨迹。保持架打滑率随转速或载荷增大而减小。
