角接触球轴承动刚度的影响因素分析
2019-07-22孙宏浩杜劲松杨旭褚云凯
孙宏浩,杜劲松,杨旭,褚云凯
(中国科学院沈阳自动化研究所 智能检测与装备研究室,沈阳 110016)
随着机床主轴特性向高速、高精度、高刚性方向发展,主轴的动态特性在其设计过程中需加以考虑。角接触球轴承作为机床主轴的核心零部件,其刚度特性直接影响主轴整体性能,故有必要对轴承刚度特性进行分析。
国内外专家学者对轴承刚度做了大量研究,文献[1]基于Hertz理论分析了滚动轴承在简单载荷下的变形及刚度计算;文献[2]分析了角接触球轴承的载荷分布,并在此基础上计算了轴承的瞬时刚度;文献[3]基于滚动轴承受力分析的拟静力学模型,计算了电主轴轴承的动态刚度。
上述文献对轴承刚度做了大量研究,但对轴承动刚度的影响因素未进行分析,鉴于此,以某角接触球轴承为研究对象,建立了轴承动刚度计算模型,并分析了转速和球材料对轴承动刚度的影响。
1 角接触球轴承拟静力学分析
如图1所示,以角接触球轴承中心为坐标原点建立坐标系,轴承外载荷可表示为
FT=[Fx,Fy,Fz,Mx,My],
(1)
式中:Fx,Fy,Fz分别为轴承在x,y,z方向的作用力;Mx,My分别为轴承绕x,y方向的力矩。
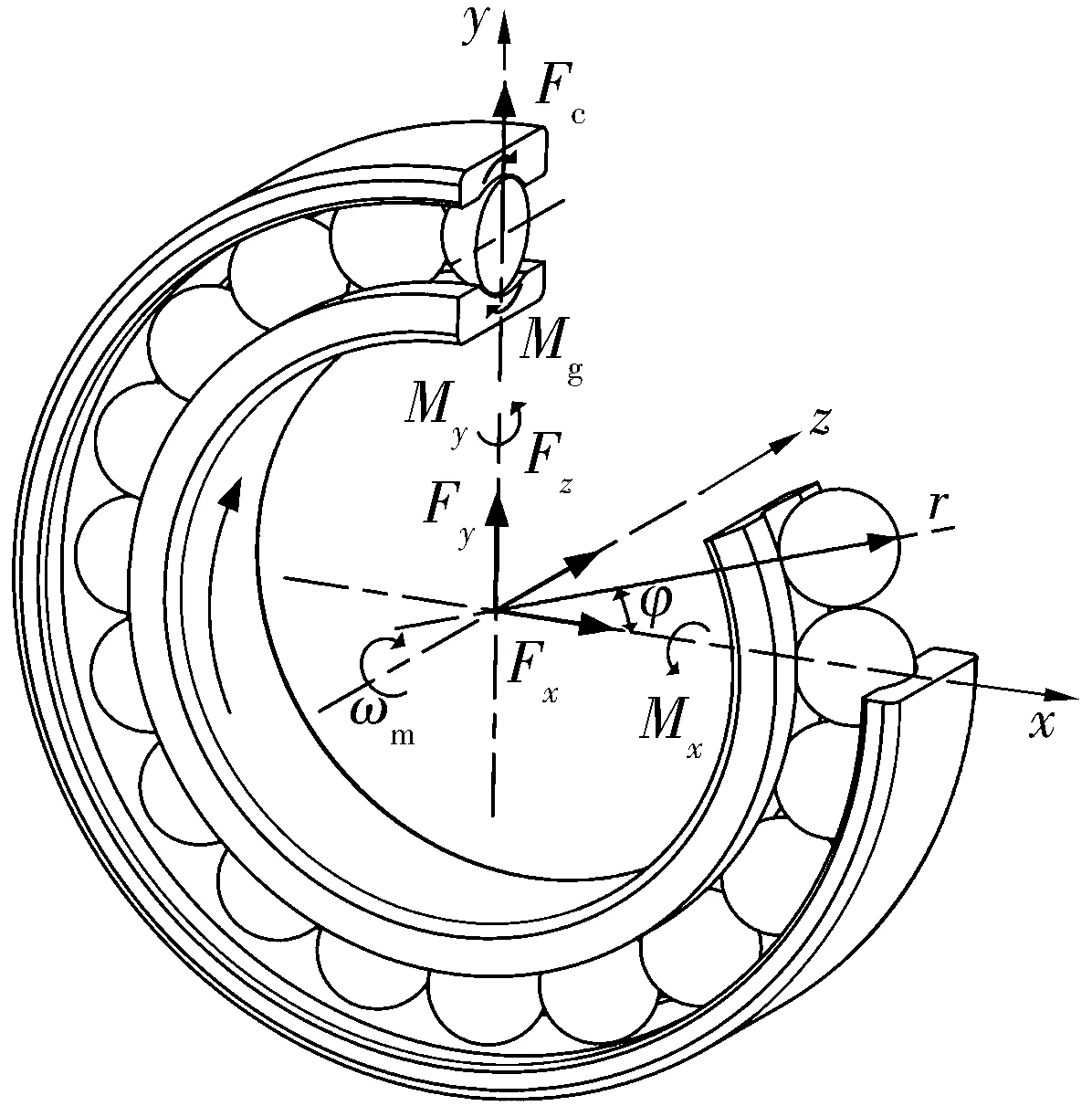
图1 轴承受载示意图
内圈在外载荷作用下的位移为
δT=[δx,δy,δz,γx,γy],
(2)
式中:δx,δy,δz分别为内圈在x,y,z方向的位移;γx,γy分别为内圈相对于x,y方向的角位移。
建立球圆柱坐标系(图2),内圈与球接触点坐标为(zp,rp,φ),接触力可表示为
QT=[Qr,Qz,T],
(3)
接触点(zp,rp,φ)位移可表示为
uT=[ur,uz,θ],
(4)
接触力与位移的关系可表示为
Q=Q(u)。
(5)
式中:Qr,Qz分别为球与内圈接触点在r,z方向的作用力;T为球与内圈接触点的作用力矩;ur,uz分别为球与内圈接触点在r,z方向的位移;θ为球与内圈接触点的角位移。

图2 球圆柱坐标系
位移u较小,可由轴承内圈整体位移δ通过坐标变换得到,即
u=Rφδ,
(6)
式中:φ为球的角位置(x正方向为0°位置)。
接触力Q乘以坐标变换矩阵,变换为作用于内圈的等效力,即
(7)
式中:Fbx,Fby,Fbz分别为球作用于内圈的等效力在x,y,z方向的分量;Mbx,Mby分别为球作用于内圈的等效力矩在x,y方向的分量。
轴承整体受力平衡方程为[4]
(8)
式中:Z为球数;j代表第j个球。
由(7),(8)式可得
(9)
(9)式为一组非线性方程,方程中未知参数δx,δy,δz,γx,γy通常采用数值法求解,采用Newton-Raphson法将(9)式转化为一组线性方程,即
(10)
Δδ=δi+1-δi,


(11)
ΔδT=[Δδx,Δδy,Δδz,Δγx,Δγy],
式中:Δδx,Δδy,Δδz分别为内圈在x,y,z方向的位移变化量;Δγx,Δγy分别为内圈在x,y方向的角位移变化量。
在轴承运转过程中,球与内、外圈沟道会发生接触变形,球心由Ob移动到O′b,内沟曲率中心由Oi移动到O′i,如图3所示。
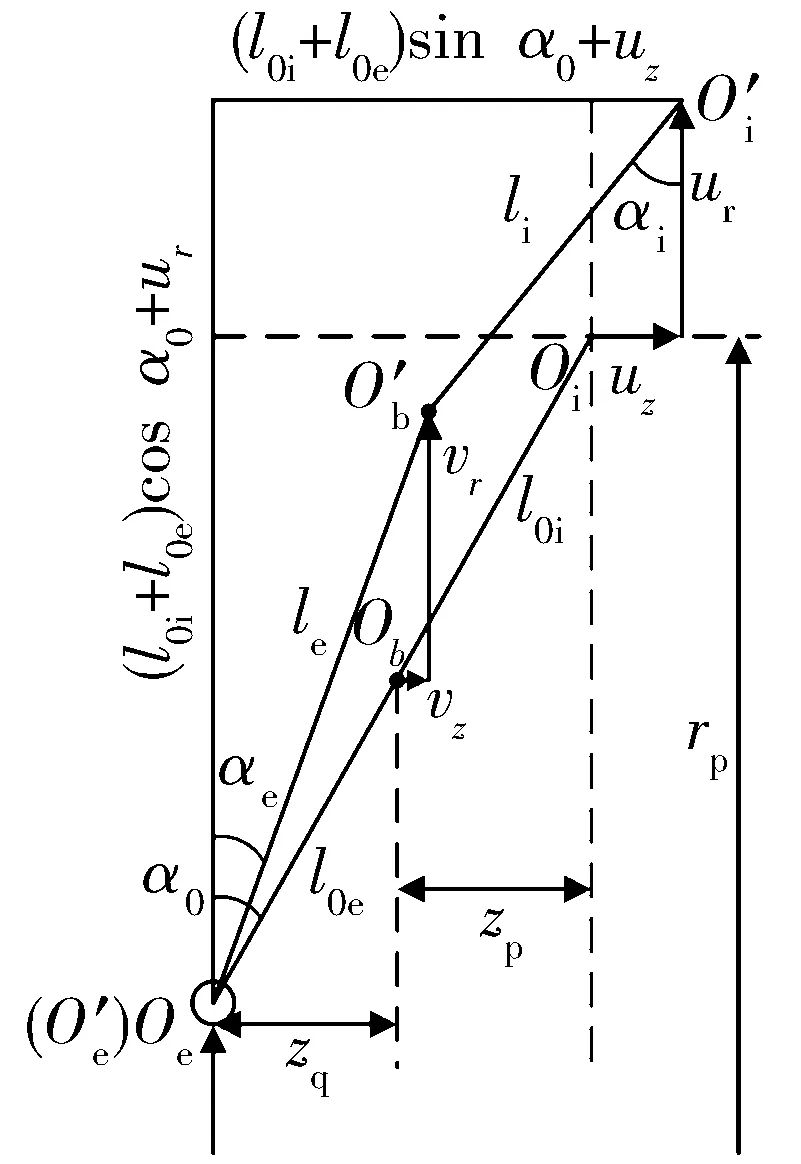
图3 球与内、外圈沟道相对位置示意图
由图3所示的几何关系可得
(12)
(13)
li=[(l0icosα0+ur-vr)2+(l0isinα0+uz-vz)2]1/2,
(14)
le=[(l0ecosα0+vr)2+(l0esinα0+vz)2]1/2,
(15)
δi=li-l0i-Δi,
(16)
δe=le-l0e-Δe,
(17)
式中:α0为初始接触角;αi,αe为球与内、外圈沟道的接触角;li,le分别为发生变形后球心与内、外沟曲率中心的距离;l0i,l0e分别为发生变形前球心与内、外沟曲率中心的距离;δi,δe分别为球与内、外圈沟道的接触变形;Δi,Δe分别表示球与内、外圈沟道之间的初始间隙。
球受力平衡方程为
(18)
式中:Qi,Qe分别为球与内、外圈的接触载荷;ci,ce可参考文献[5]计算。
球受到内圈的接触力为
(19)
未知参数球中心位移向量(vr,vz)采用Newton-Raphson法求解,定义(Δvr,Δvz)为下步迭代中未知量变化量,(18)式可转化为
(20)
对(20)式求导可得

(22)


2 角接触球轴承动刚度计算
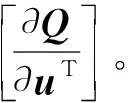
(24)
为方便计算,定义接触力向量Q-、内沟曲率中心位移向量u-和球位移向量v-分别为[5]
(25)
(26)
(27)
其中w-=u--v-。
推导可得
(28)
定义
(29)
(30)
(31)
球受力平衡方程可表示为
(32)
(20)式中的Jacobian矩阵可表示为

(33)
即
JB=JBi+JBe。
(34)
(32)式对u-求导可得
(35)
(35)式可转化为
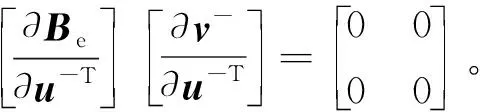
(36)
w-对v-求导,可得
dw-=-dv-,
(37)
联立(25)—(37)式可得
(38)
联立(21),(22),(23),(30),(31)式可得

(39)
(40)
通过迭代求解可得接触刚度矩阵为
(41)
3 实例分析
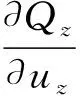
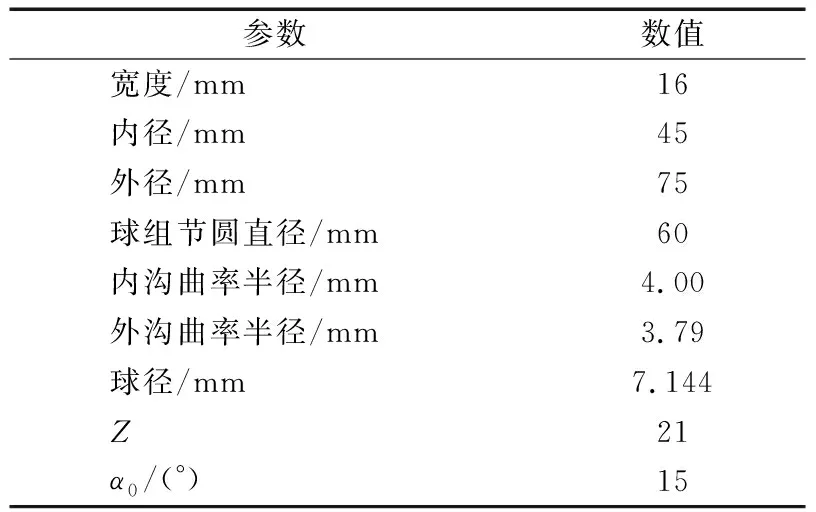
表1 角接触球轴承主要结构参数
3.1 转速对轴承动刚度的影响
内、外圈材料为GCr15Z,球材料为Si3N4,在不同预紧力Fz下轴承刚度随转速的变化如图4所示,由图可知:随转速增大,轴承轴向和径向刚度先减小后趋于稳定;当转速小于1.7×104r/min时,预紧力对轴承轴向和径向刚度的影响较大,当转速大于1.7×104r/min时,预紧力对轴承径向和轴向刚度的影响较小。
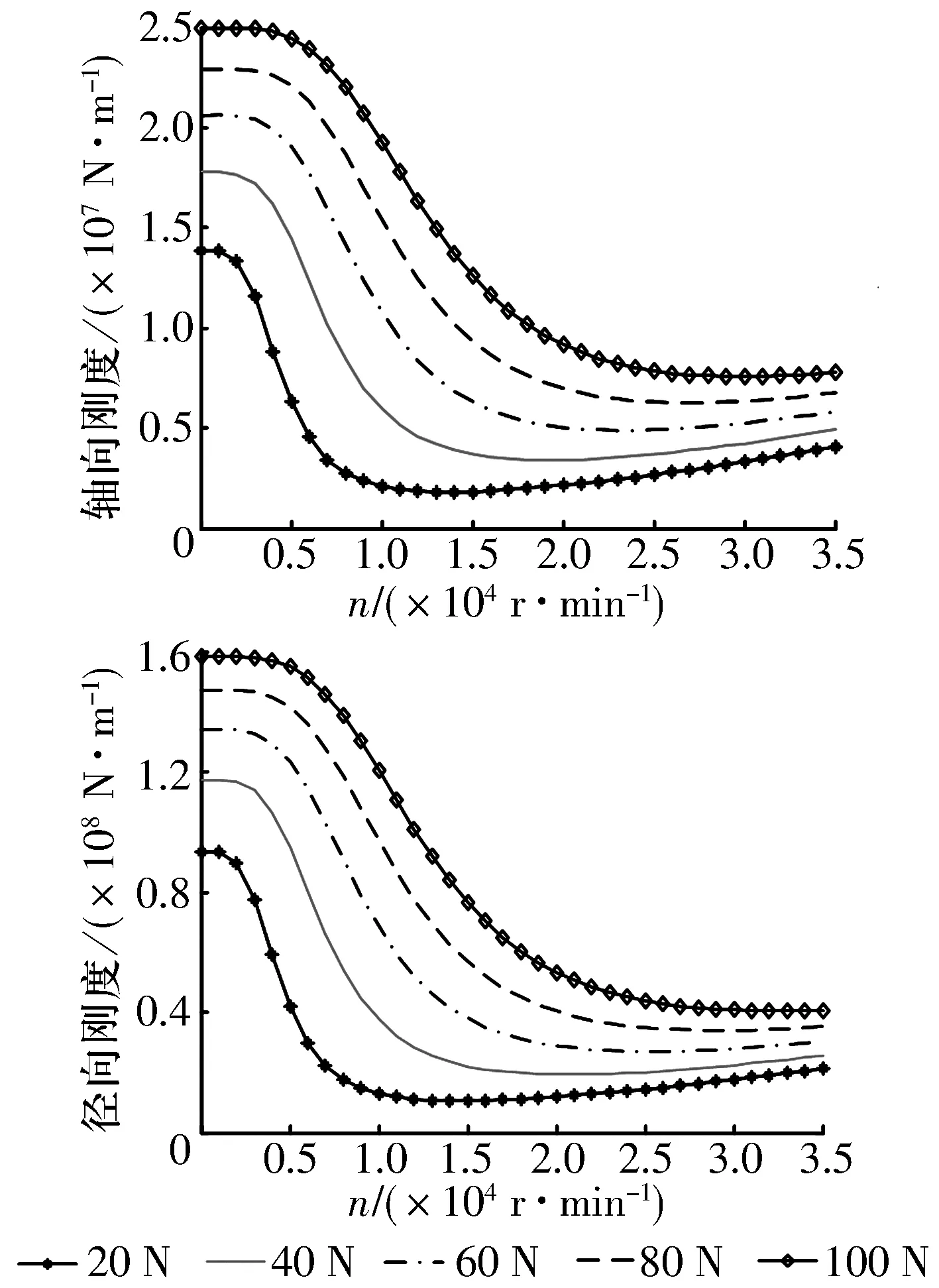
图4 转速对轴承刚度的影响
3.2 球材料对轴承刚度的影响
轴承套圈材料选用GCr15Z,球材料分别为Si3N4,GCr15Z,ZrO2及SiC时,轴承刚度随转速的变化如图5所示。由图可知:1)球材料变化时,轴承轴向和径向刚度随转速的变化曲线随之改变,但总体变化趋势相同;2)球材料为Si3N4,SiC时,轴向和径向刚度随转速的变化曲线比较接近,球材料为GCr15Z,ZrO2时,轴向和径向刚度随转速的变化曲线比较接近;3)当转速小于2.0×104r/min时,球材料为Si3N4,SiC时轴承的轴向和径向刚度比球材料为GCr15Z,ZrO2时的要大,当转速大于2.5×104r/min时,球材料为GCr15Z,ZrO2时轴承的轴向和径向刚度比球材料为Si3N4和SiC时的大。这是由于材料密度会影响物体的惯性力矩及质量,材料弹性模量和泊松比会影响两物体接触形变量,从而影响轴承刚度。
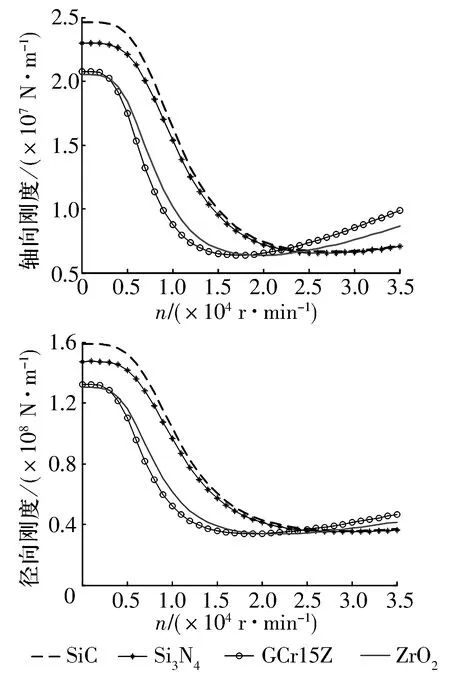
图5 球材料对轴承刚度的影响
4 结论
1)随转速增大,轴承轴向和径向刚度会先减小后趋于稳定;
2)球材料的选择会对轴承刚度产生影响,球材料为Si3N4,SiC时,轴承轴向和径向刚度随转速的变化曲线比较接近,球材料为GCr15Z,ZrO2时,轴承轴向和径向刚度随转速的变化曲线比较接近;
3)当转速小于2.0×104r/min时,球材料为Si3N4,SiC时轴承轴向和径向刚度比球材料为GCr15Z,ZrO2时的要大,当转速大于2.5×104r/min时,球材料为GCr15Z,ZrO2时轴承轴向和径向刚度比球材料为Si3N4和SiC时的大。
