高速铁路轮轨动力作用规律分析

涂英辉

（中国铁道科学研究院集团有限公司 铁道建筑研究所，北京   100081）

目前，我国350 km/h及以下速度等级高速铁路固定设施设计施工技术日趋完善，技术标准基本齐备[1]，并对该速度等级的高速铁路轮轨关系、轮轨周期性磨耗条件下的轮轨动力作用进行了专项试验研究[2-6]。但对于更高速度等级的轮轨动力作用研究尚处于探索阶段，确定更高速度条件下的轮轨动力作用规律，对于指导轮轨材料和结构优化升级，提高我国高速铁路相关工程设计施工水平具有重要意义，同时可为下一阶段我国高速铁路的建设规划及推动高速铁路行业进一步发展提供技术支撑和依据。

1 常规状态下轮轨动力作用

为分析380 km/h和400 km/h更高速度动车组在轮轨常规状态下的适应性，分别进行现场综合试验和理论分析。其中现场综合试验包括京沪高铁先导段（枣庄西—蚌埠南）和郑徐高铁开封北—萧县北段[7]。

1.1 试验分析

1.1.1 京沪高铁先导段

京沪高铁先导段（枣庄西—蚌埠南）为直线地段，采用CRTS Ⅱ型板式无砟轨道，配套W300-1型扣件，下部基础为路基。主要测试车型为中车青岛四方机车车辆股份有限公司制造的CRH380AL和中车唐山机车车辆有限公司制造的CRH380BL，分别测试300、330、350、380、400 km/h速度等级条件下的轮轨垂向力情况，测试结果见表1。

表1 京沪高铁先导段轮轨垂向力测试结果

由表1可知，高速动车组通过各轮轨力测点时轮轨垂向力最大值为87.5～98.6 kN，平均值为69.3～77.9 kN。相比350 km/h及以下速度等级，高速动车组以380 km/h和400 km/h速度通过直线区段时的轮轨动力作用变化不明显。

1.1.2 郑徐高铁

郑徐高铁试验区段开封北—萧县北为曲线地段，采用CRTS Ⅲ型先张板式无砟轨道、WJ-8型扣件，桥上除连续梁及紧靠连续梁一跨的简支梁采用小阻力扣件外，其余简支梁采用常阻力扣件。主要测试车型为CRH0207和CRH0503型动车组，分别进行300、330、350、380和400 km/h不同速度等级条件下，动车组通过半径为9 000 m曲线缓圆点时的轮轨垂向力情况，测试结果见表2。

表2 郑徐高铁试验段轮轨垂向力测试结果

由表2可知，随着列车速度的增加，轮轨垂向力幅值略有增大。动车组以380、400 km/h速度通过半径为9 000 m曲线缓圆点时，实测轮轨垂向力最大值分别为 115.8 kN 和 125.1 kN，平均值分别为 93.6 kN 和97.1 kN，均未超出《高速铁路工程动态验收技术规范》[8]中轮轨动力作用的限值要求（170 kN）。

综合京沪高铁先导段和郑徐高铁试验分析可知，在轮轨常规状态下，随着列车速度的增加，轮轨动力作用不断增大，但增大幅度较小。400 km/h与300 km/h速度相比，最大轮轨垂向力增大约40%，平均轮轨垂向力增大约29%；400 km/h与350 km/h速度相比，最大轮轨垂向力增大约20%，平均轮轨垂向力增大约12%。最大轮轨垂向力均未超出《高速铁路工程动态验收技术规范》中轮轨动力作用的限值要求。

1.2 理论分析

利用NUCARS分析软件，参照CRH380A型动车组建立车辆-轨道耦合动力学仿真模型（见图1）[9]。该模型由1个车体、2个构架、4个轮对构成，其中每个刚体均考虑垂向、横向、纵向、点头、摇头和侧滚6个自由度。构架和轮对之间通过一系弹簧、垂向减振器连接，构成一系悬挂系统；构架和车体之间通过空气弹簧、二系垂向减振器、二系横向减振器、抗蛇行减振器等元件连接，构成二系悬挂系统，悬挂系统由弹簧阻尼单元模拟。钢轨采用离散点支承形式，由弹簧阻尼单元模拟扣件垂向和横向的约束作用，同时考虑钢轨表面原始不平顺的影响。模型主要参数见表3。

图1 车辆-轨道耦合动力学仿真模型

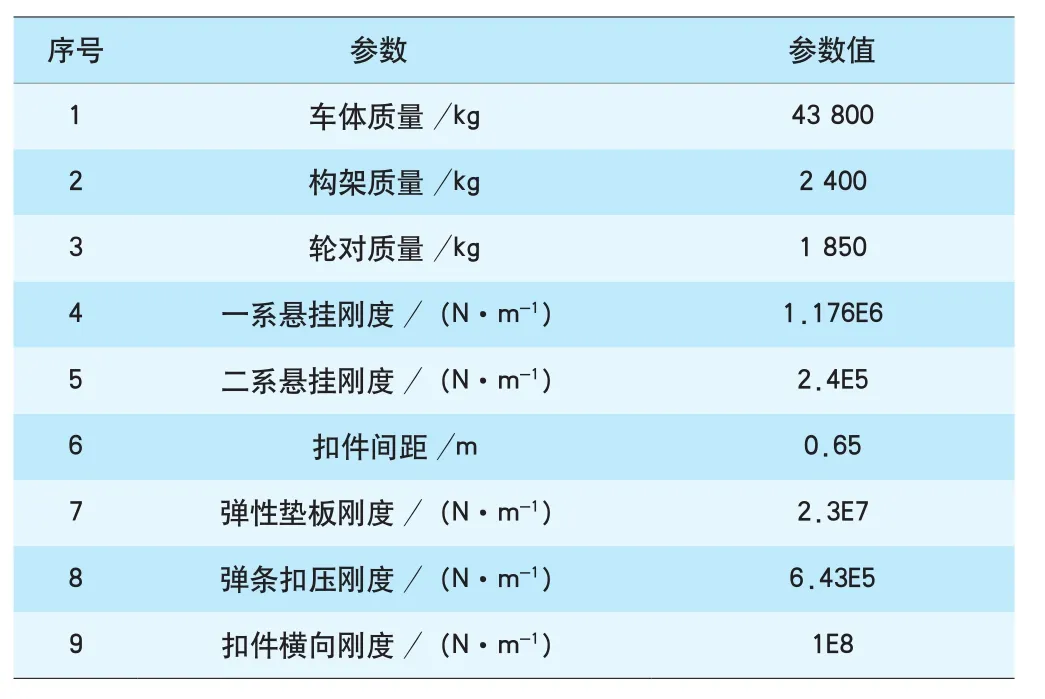
表3 车辆-轨道动力学仿真模型主要参数

采用车辆-轨道耦合动力学仿真模型，分析在轮轨常规状态下，列车分别以300、350、380和400 km/h速度通过时的轮轨动力作用最大值（见表4）。

表4 常规状态下轮轨动力作用最大值

由表4理论分析结果可知，在轮轨常规状态下，随着列车速度的增加，轮轨动力作用略有增大，但增大幅度较小。400 km/h与300 km/h速度相比，最大轮轨垂向力增大约31%；400 km/h与350 km/h速度相比，最大轮轨垂向力增大约19%。最大轮轨垂向力均未超出《高速铁路工程动态验收技术规范》中轮轨动力作用的限值要求。

2 钢轨波磨条件下轮轨动力作用

为分析钢轨表面存在波磨的情况下，不同速度动车组通过时的轮轨动力作用，分别进行现场试验和理论分析。其中现场试验为2011年京沪高铁钢轨波磨专项试验[10]。

2.1 试验分析

2011年对京沪高铁不同波磨深度情况下的轮轨动力作用进行了专项试验。京沪高铁采用CRTS Ⅱ型板式无砟轨道，配套W300-1型扣件，钢轨表面存在明显波磨，波长为120～150 mm，分别在波磨谷深0.04、0.05和0.08 mm位置及无波磨区段测试轮轨动力作用情况，测试结果表明：

（1）波磨谷深0.04 mm地段。在250 km/h速度等级下，有波磨地段轮轨垂向力平均值比无波磨地段增大约8.8%；在300 km/h速度等级下，轮轨垂向力平均值增大约20.8%。

（2）波磨谷深0.05 mm地段。在250 km/h速度等级下，有波磨地段轮轨垂向力平均值比无波磨地段增大约13.0%；在300 km/h速度等级下，轮轨垂向力平均值增大约52.5%。

（3）波磨谷深 0.08 mm 地段。在 250 km/h速度等级下，有波磨地段第一、二、三断面轮轨垂向力平均值比无波磨地段分别增大27.1%、33.4%、36.2%；在300 km/h速度等级下，轮轨垂向力平均值分别增大61.9%、93.5%、82.8%。

综合分析动车组高速通过有波磨测点产生的轮轨垂向力测试数据可知，钢轨波磨对轮轨垂向力有较大影响，相同速度条件下磨耗深度越大，轮轨动力作用越大。与无波磨地段相比，在250 km/h速度等级下有波磨地段轮轨垂向力增大的幅度为8.8%～36.2%，在300 km/h速度等级下有波磨地段轮轨垂向力增大的幅度为20.8%～93.5%，实测轮轨垂向力最大值为168 kN（接近170 kN限值），出现在波磨谷深0.08 mm地段。

2.2 理论分析

利用车辆-轨道耦合动力学仿真模型，分析钢轨表面存在波长为120～150 mm，波磨谷深0.02、0.04、0.06和0.08 mm以及无波磨时，行车速度为300、350、380和400 km/h时的轮轨力情况，计算得到不同钢轨磨耗程度和不同行车速度下的轮轨垂向力最大值变化规律，未考虑车轮多边形条件的计算结果见图2。

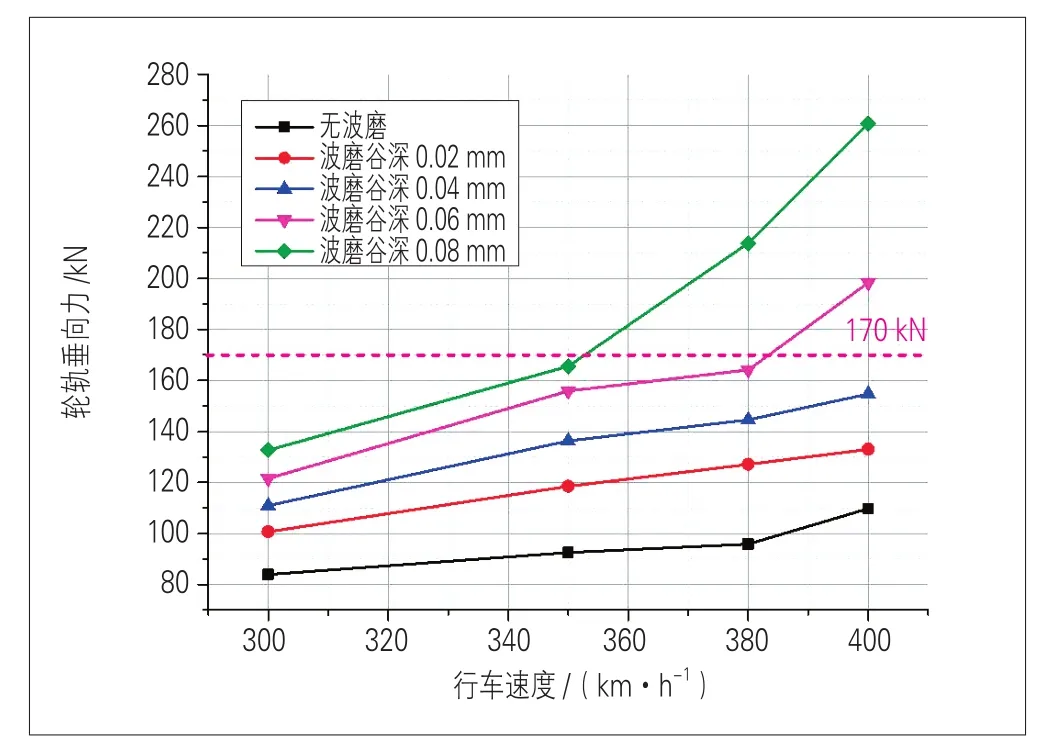
图2 不同钢轨波磨和不同行车速度时的轮轨垂向力

由图2可知，相同速度等级条件下，波磨谷深越大，轮轨动力作用越大，400 km/h速度时，波磨谷深0.08 mm与0.02 mm相比，轮轨垂向力增大约96%；相同波磨谷深条件下，速度越大，轮轨动力作用越大，波 磨 谷 深 0.08 mm 时，400 km/h 与 300 km/h 速 度 相比，轮轨垂向力增大约63%。350 km/h速度情况下，波磨谷深0.08 mm时轮轨垂向力接近170 kN的限值要求；380 km/h速度情况下，波磨谷深0.06 mm时轮轨垂向力接近170 kN的限值要求；400 km/h速度情况下，波磨谷深0.06 mm时轮轨垂向力超过170 kN限值要求。

3 车轮多边形条件下轮轨动力作用

为分析车轮表面存在多边形的情况下，动车组以不同速度运行时的轮轨动力作用，分别进行现场试验和理论分析。其中现场试验为2016年武广高铁车轮多边形专项试验[11]。

3.1 试验分析

2016年对武广高铁车轮多边形情况下的轮轨动力作用进行了专项试验。武广高铁采用CRTS Ⅰ型双块式无砟轨道，配套W300-1型扣件，在武广高铁牛岭隧道K2096+211—K2103+799区段进行了车轮多边形专项试验。牛岭隧道测点线路曲线半径为11 005 m，超高为 115 mm，3.0‰上坡，钢轨光带宽度为 20～25 mm，钢轨为近期打磨状态，表面无明显波磨。试验动车组车轮中存在18阶多边形，平均径跳值为0.06 mm。

分别测试试验动车组以250、280和300 km/h速度通过测点时的轮轨垂向力情况，测试结果见表5。

表5 试验动车组车轮有无多边形、不同速度时的轮轨动力作用

由表5可知，相同速度等级条件下，车轮有多边形与无多边形相比，轮轨动力作用增大，但增大幅度较小，300 km/h速度下，径跳值0.06 mm时的轮轨垂向力与无多边形相比增大幅度为13%；相同多边形条件下，随着速度的增加，轮轨动力作用增大，径跳值0.06 mm时， 300 km/h与250 km/h速度相比，轮轨垂向力增大幅度为23.6%。

3.2 理论分析

利用车辆-轨道耦合动力学仿真模型，分别分析车轮表面存在18阶多边形，径跳值为0.02、0.04、0.06和0.08 mm 时，行车速度为 300、350、380和 400 km/h的轮轨垂向力情况，计算得到不同车轮多边形程度和不同行车速度下的轮轨垂向力变化规律（见图3）。

图3 不同车轮多边形和不同行车速度时的轮轨垂向力

由图3可知，相同速度等级条件下，车轮多边形径跳值增大，轮轨动力作用略有增大，400 km/h速度下，径跳值0.08 mm与0.02 mm相比，轮轨垂向力增大约7%；相同车轮多边形径跳值条件下，速度越大，轮轨动力作用越大，径跳值为 0.08 mm 时，400 km/h与 300 km/h速度相比，轮轨垂向力增大约20%。

4 结论

通过对轮轨常规状态、钢轨波磨和车轮多边形等条件下，动车组不同速度等级运行时的轮轨动力作用进行现场试验和理论分析研究，得出初步结论如下：

（1）在轮轨常规状态下，随着速度的增加，轮轨动力作用略有增大，但增大幅度较小。400 km/h与300 km/h速度相比，最大轮轨垂向力增大约40%；400 km/h与350 km/h速度相比，最大轮轨垂向力增大约20%。最大轮轨垂向力均未超出《高速铁路工程动态验收技术规范》中轮轨动力作用的限值要求。

（2）钢轨波磨条件下轮轨动力作用明显增加。相同速度等级条件下，波磨谷深越大，轮轨动力作用越大，400 km/h 速度时，波磨谷深 0.08 mm 与 0.02 mm 相比，轮轨垂向力增大约96%；相同磨耗程度条件下，速度越大，轮轨动力作用越大，波磨谷深0.08 mm时，400 km/h与 300 km/h速度相比，轮轨垂向力增大约63%。350 km/h速度情况下，波磨谷深0.08 mm时轮轨垂向力接近170 kN限值要求；380 km/h速度情况下，波磨谷深0.06 mm时轮轨垂向力接近170 kN限值要求；400 km/h速度情况下，波磨谷深0.06 mm时轮轨垂向力超过170 kN限值要求。

（3）车轮多边形磨耗条件下轮轨动力作用增大。相同速度等级条件下，车轮多边形径跳值增大，轮轨动力作用略有增加，400 km/h速度时，径跳值0.08 mm与0.02 mm相比，轮轨垂向力增大约7%；相同车轮多边形径跳值条件下，速度越大，轮轨动力作用越大，径跳值 0.08 mm 时，400 km/h 与 300 km/h 速度相比，轮轨垂向力增大约20%。