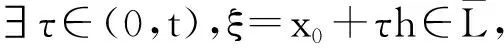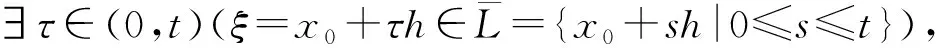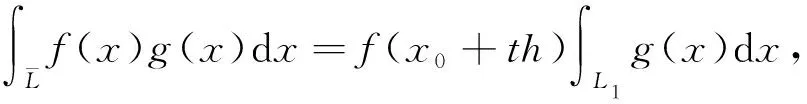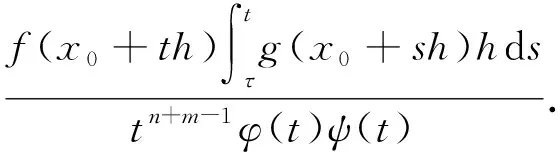泛函积分中值定理“中间点”的渐近性
2019-07-20张芯语张树义
张芯语,张树义,聂 辉
(渤海大学数理学院,辽宁 锦州 121013)
1 引言与预备知识
AZPEITJA[1]研究了Taylor公式“中间点”的渐近性质. 同时, JACOBSON[2]建立积分中值定理的类似的结果. 在这之后, 一些作者研究各种中值定理“中间点”的渐近性质[3-14],其中文献[3]研究了泛函积分中值定理“中间点”的渐近性.文献[4-7]使用比较函数讨论了包括泛函Taylor公式在内的几种中值定理“中间点”的渐近性态. 文献[15-22]研究了几种中值定理“中间点函数”的一阶可微性, 本文的目的是使用比较函数研究泛函积分中值定理“中间点”的渐近性,获得的结果推广和改进了文献[3]以及有关文献中的相应结果.
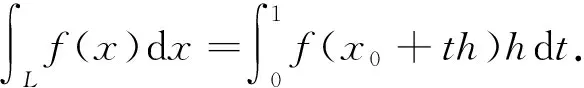
泛函第一积分中值定理[3]设f(x)是Ω⊂X上的连续泛函,对x0∈Ω,h∈X,g(x)是L={x0+th|0≤t≤1}⊂Ω上的非负连续泛函,则存在ξ=x0+τh∈L,τ∈(0,1),使
定义2[3]设x0∈Ω,h∈X,L={x0+th|0≤t≤1}⊂Ω.如果∀t1,t2∈[0,1],当t1≥t2时,有f(x0+t1h)≥f(x0+t2h)(f(x0+t1h)≤f(x0+t2h)), 则称f在L上单调递增(减)泛函.
泛函第二积分中值定理[3]设X是赋范线性空间,Ω⊂X是凸开集,f是定义在L={x0+th|0≤t≤1}上的非负单调递增连续泛函,g是L上可积泛函,则∃τ∈(0, 1)(ξ=x0+τh∈L),使
其中L2={x0+th|τ≤t≤1}.
推论1[3]设X是赋范线性空间,Ω⊂X是凸开集,f是L上单调非负连续泛函,g在L上可积,则∃τ∈(0,1)(ξ=x0+τh∈L),使
其中L1={x0+th|0≤t≤τ},L2={x0+th|τ≤t≤1}.
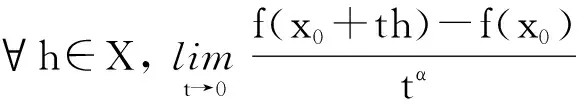
定义4[4]设ψ为定义在L={x0+th|0≤t≤1}上的泛函,在半开区间(0, 1]上存在m(m≥1)阶导数的实值函数φ(t)被称为在L上关于泛函ψ(x0+th)的比较函数, 如果满足下列条件:
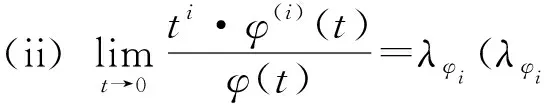

注1 如果定义1中Dαf(x0,h)非零, 则φ(t)=tα是关于f(x0+th)-f(x0)的比较函数.
引理1[5]设x>0,φ(x)=xα,α为实数且α>-1,n≥1,Γ(·)为Gamma函数, 则
其中
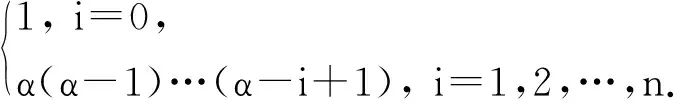
2 主要结果
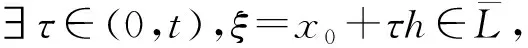
且

证明 由定理1条件可设
其中A,B是非零常数.由泛函第一积分中值定理知∃τ∈(0,t),使
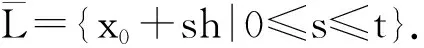
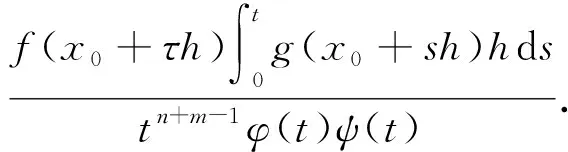
(1)
式(1)左边
式(1)右边

(2)
由式(1)与(2)立得
证毕.

推论2 设X是赋范线性空间,Ω是X中凸开集,∀x0∈Ω,h∈X,f是L={x0+th|0≤t≤1}上的连续泛函且在L上n-1阶F-可微,f(i)(x0)h(i)=0(0≤i 且 其中x=x0+th∈L,A,B是非零常数,α,β是实数且α>0, β≥0. 注2 推论2比文献[3]中定理2.1简洁. (3) 且 其中L1={x0+sh|τ≤s≤t}. 证明 由泛函第二积分中值定理知式(3)成立. 由式(3)易知 (4) 式(4)左边 式(4)右边 (5) 由式(4)与(5)立得 且 其中x=x0+th∈L,L1={x0+sh|0≤s≤τ},L2={x0+sh|τ≤s≤t}.