三塔大跨斜拉桥风致响应研究
2019-07-20张明金严乃杰
陈 强, 张明金, 严乃杰
(西南交通大学土木工程学院, 四川成都 610031)
随着我国经济的高速发展,人们对交通运输业的需求与日俱增,桥梁的建造技术得到相应发展,大跨度桥梁不断涌现,例如明石海峡大桥、泰州长江公路大桥以及正在修建的墨西拿海峡大桥等大跨度悬索桥[1-4],墨西哥墨兹卡拉大桥、香港汀九大桥和岳阳洞庭湖大桥等大跨度斜拉桥[5-8]。而随着桥梁跨度不断增大,桥梁结构变得越来越柔,对风荷载越来越敏感,桥梁风毁事故也频频发生。自1940年塔科马大桥风毁事故起,桥梁结构风致振动受到重视,大量学者对其发生机理进行深入研究。例如Theodorsen于1934年首次提出了结构发生颤振失稳的基本原理[9];1962年,Davenport估计了桥梁结构的抖振响应[10];1977年,Scanlan对Davenport的经典抖振模型进行了修正[11]。目前,精细化地研究大跨度桥梁风致振动机理已成为重点方向[12-13],其中包括各类复杂地形对风场的影响[14-15],大跨度桥梁结构的抗风性能成为设计过程中所必须考虑的关键因素[16]。
由于斜拉桥具有经济、施工方便等的优点,斜拉桥的建造越来越多,斜拉桥的抗风性能也是设计过程中重点研究对象。文献[17]~[21]对独塔斜拉桥和双塔斜拉桥的抗风稳定性进行了研究,分析对比了主梁截面型式,桥塔结构形式、主梁宽度、桥墩间距和桥塔高跨比等设计参数对桥梁抗风性能的影响。随着交通的进一步发展,三塔斜拉桥也逐渐出现,而目前少有文献对三塔大跨斜拉桥风致响应进行研究,因此,研究三塔大跨斜拉桥的风致响应具有一定的意义。本文以某三塔大跨斜拉桥为例,计算分析了三塔大跨斜拉桥在静风和脉动风作用下主梁的风致响应特征。
1 桥梁简介
该三塔斜拉桥整体布置见图1,跨径布置为45 m+120 m+2×400 m+120 m+45 m,两侧边跨分别设置一个辅助墩和一个过渡墩。中间塔高约为180 m,两侧塔高约为160 m。主梁宽32 m,高3 m,其中边跨51 m范围为混凝土梁,其余梁段为工字钢和混凝土板的叠合梁。

图1 整体布置(单位:m)
2 桥址区风特性
2.1 风速标准
桥址区位于低层建筑稀少地区,根据文献[22],该地区地表类型取为B类,地表粗糙度取0.16,百年一遇10 min,年平均最大风速V10=24.3m/s。主梁与平均通航水位距离d=65.85m,风速沿高度变化的修正系数K1B=1.0×(d/10)0.16=1.352,则桥面高程处设计基准风速为U(d)=K1B×V10=32.9m/s。
2.2 风谱特性
在缺少抖振场实测数据的情况下,在水平方向和竖直方向的抖振风速功率谱分别采用以下公式[22]:
(1)
(2)
式中:Su(n)为抖振水平方向的功率谱密度函数;Sw(n) 为抖振竖直方向的功率谱密度函数;n为风的频率;f为折算频率;u*为气流摩擦速度。
3 桥梁有限元模型
采用ANSYS对桥梁结构进行离散,其中,主梁、桥塔和桥墩采用梁单元Beam4模拟,斜拉索采用杆单元Link8模拟,二期荷载采用质量点单元Mass21模拟,成桥状态有限元模型见图2,动力特性主要频率和振型见表1。

图2 有限元模型

表1 动力特性计算结果
4 风致效应计算
4.1 静力气动力参数计算


图3 成桥状态主梁静力三分力系数
采用计算流体动力学软件FLUENT求解,桥塔典型截面见图4,静风气动力参数采用结构化网格划分的定常计算方式,选用SSTk-ω湍流模型,压力-速度耦合问题采用SIMPLEC算法。最后求得在平均风风偏角β=0°时,桥塔断面阻力系数CD(β)为2.058,升力系数CL(β)为0.038和力矩系数CM(β)为0.012。

图4 桥塔典型截面(单位:m)
4.2 静风及抖振响应计算
静风作用下的响应为结构在自重作用下,各个构件受到静风作用时的位移及内力。
静风作用下,各构件静风阻力FD、静风升力FL及静风力矩FM[22]分别为:
(3)
(4)
(5)
式中:ρ为空气密度;H为构件高;B为构件宽;L为构件度。
脉动风作用下的响应分析基于随机理论,采用多模态耦合分析的频域分析法[22-25]。脉动阻力D、脉动升力L及脉动阻力M分别由自激力和抖振力组成:
D=Dae+Dbu
(6)
L=Lae+Lbu
(7)
M=Mae+Mbu
(8)
式中:Dae为自激阻力;Lae为自激升力;Mae为自激力矩;Dbu为抖振阻力;Lbu为抖振升力;Mbu为抖振力矩。
自激力采用Scanlan表达形式,抖振力采用准静态表达,抖振位移响应均方根通过对结构抖振响应功率谱密度函数积分得到,抖振内力响应采用SRSS方法进行组合。
5 计算结果及分析
采用桥面高程处设计基准风速U(d)=32.9m/s,经数值模拟计算分析,主梁在静风作用和脉动风作用下的风致动力响应如图5和图6所示。

(a) 主梁静风位移响应

(b) 主梁抖振位移响应图5 主梁风致位移响应
由图5(a)可知,在静风作用下,主梁横桥向及竖向线位移在3#、4#和5#塔梁结合处、辅助墩及过渡墩处接近于0。横桥向和竖向线位移极大值均在单跨跨中,其中横桥向线位移最大值约为7 mm,竖向线位移最大值约为27 mm。顺桥向线位移主要由竖向线位移引起,最大值约为1 mm。主梁静风线位移以竖向线位移为主,顺桥向及横桥向线位移较小。
由图5(b)可知,在脉动风作用下,主梁抖振竖向线位移在3#、4#和5#塔梁结合处、辅助墩及过渡墩处接近于0。抖振竖向线位移极大值在单跨跨中,其中最大值约为20 mm。主梁抖振线位移以竖向线位移为主,顺桥向及横桥向线位移较小。
因主梁截面整体抗弯扭刚度较大,静风扭转角及抖振扭转角均较小。由图6(a)可知,在静风作用下,主梁横桥向和竖向剪力在3#、4#和5#塔梁结合处存在突变点。横桥向和竖向剪力最大值在4#塔桥结合处,分别约为200 kN和640 kN。轴力极大值在3#、4#和5#塔梁结合处,其中最大值约为1 500 kN。因桥梁结构对称特性,三个方向截面力近零值点均在单跨跨中。主梁静力轴力较横桥向及竖向剪力大。
由图6(c)可知,在脉动风作用下,主梁抖振轴力极大值在3#、4#和5#塔梁结合处,其中最大值约为530 kN。横向剪力在辅助墩处达到最大值,约为150 kN。主梁抖振轴力较横桥向剪力及竖向剪力大得多。
由图6(b)可知,在静风作用下,主梁横桥向弯矩极大值在3#、5#塔梁结合处及单跨跨中,其中最大值约为35 000 kN·m。主梁静风横桥向弯矩较扭矩及竖向弯矩大得多。
由图6(d)可知,在脉动风作用下,主梁抖振横桥向弯矩极大值在3#、4#和5#塔梁结合处及单跨跨中,其中最大值约为18 000 kN·m。竖向弯矩极大值出现在4#塔梁结合处、单跨跨中及辅助墩处,其中最大值约为20 000 kN·m。主梁抖振横桥向弯矩及竖向弯矩较扭矩大得多。

(a) 主梁静风力

(b) 主梁静风力矩
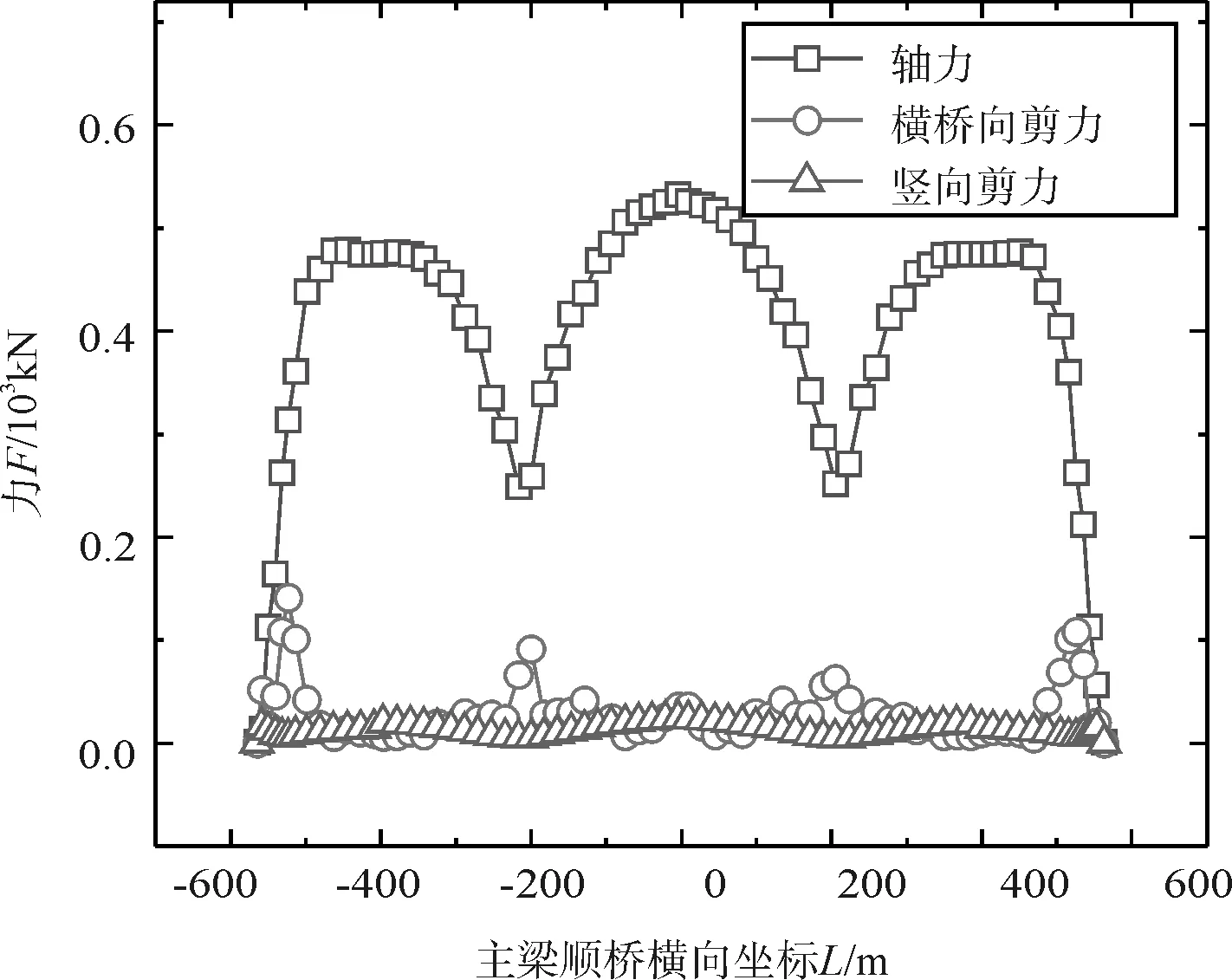
(c) 主梁抖振力

(d) 主梁抖振力矩
6 结论
对三塔大跨斜拉桥成桥状态风致响应进行了数值模拟计算,通过对比主梁各节点位移和内力,可得出以下结论:
(1)静风作用下,主梁以竖向线位移为主,顺桥向和横桥向线位移较小。主梁截面轴力和竖向剪力较大,横桥向剪力较小,截面横桥向弯矩较扭矩及顺桥向弯矩大。
(2)脉动风作用下,主梁抖振以竖向线位移为主,顺桥向和横桥向线位移较小,且抖振线位移较静风线位移小。主梁截面以轴力为主,横桥向剪力和竖向剪力相对较小,截面弯矩以横桥向和竖向弯矩为主,扭矩相对较小。
(3)因桥塔、桥墩的约束以及主梁截面抗弯扭刚度较大,主梁的静风和抖振扭转角均较小。
