农村居民点综合破碎度评价及影响因素探测*
——以山东日照市为例
2019-07-20齐文平王艳慧梁晨霞
齐文平,王艳慧,梁晨霞,程 序
(1.中电科大数据研究院有限公司,贵州贵阳 550022; 2.首都师范大学资源环境与地理信息系统北京市重点实验室,北京 100048; 3.首都师范大学三维信息获取与应用教育部重点实验室,北京 100048; 4.首都师范大学城市环境过程与数字模拟国家重点实验室培育基地,北京 100048)
0 引言
社会主义新农村建设,是我国统筹城乡发展与构建和谐社会的重大战略部署[1]。及时、准确地掌握农村居民点信息是推进“城乡一体化”和新农村建设的基础[1]。土地整理是一项消耗资金大、时间跨度大的复杂工程,在选择整理模式时,必须充分考虑项目区特点、阻碍因素和土地主要用途,综合分析进行选择。从已有的研究成果可以发现,当前针对农村居民点的研究主要集中在3个方面:农村居民点空间分布特征分析与布局优化、农村居民点用地适宜性评价和农村居民点整理潜力测算[5-15]。近年来,不少学者对农村居民点空间分布特征及其影响因素进行了大量的研究,如徐威杰等[5]基于GIS和景观格局指数在镇级尺度下对农村居民点分布状况进行研究,对农村居民点潜在分布规律进行挖掘; 刘仙桃等[6]基于Voronoi图在镇级尺度下对北京市昌平区农村居民点分布状况进行研究,并定量分析了各因素对空间分布的影响; 部分学者在行政村尺度下分别从人文和自然的角度构建了综合离散度评价模型,并剖析了其与农村经济的关联关系[7-9]; 钟紫玲[10]基于Voronoi图和景观指数法在镇级尺度下分析了山区农村居民点的空间分布特征。以上研究主要是针对内陆山区农村居民点的空间分布及影响因素方面,然而其评价指标及评价方法缺乏普适性。尤其对于东部沿海平原地区,其正处于城市化和工业化高速发展时期,地区农村人口的非农化转移,并未带来农村居民点用地的相应减少,而是呈现逐渐增大的趋势,形成了沿海地区农村居民点用地增长快、布局散、总量大、闲置多的显著特点[1]。其破碎程度导致村庄管理和公共基础设施的集中建设比较困难,居民收入差距不断拉大,成为东部沿海地区推进新农村建设和率先基本实现现代化面临的核心问题。因此,基于沿海平原地区农村居民点分布的特殊性,考虑很多省市地方政府部门已经将土地整治权限下放到乡镇,文章在镇级尺度下构建了农村居民点破碎度评价模型,定量评价沿海平原地区的农村居民点规模、形状和分布特征,并运用多元回归模型对破碎度的因素影响进行定量分析,提出针对性的土地整理模式政策建议,为城乡协调发展和新农村建设的土地利用决策提供参考依据。

图1 研究区概况
1 研究区概况和数据来源
1.1 研究区概况
日照市位于黄海之滨,地处山东半岛东南部。全市总面积为5 358.57km2,其中山地占19.7%,丘陵占52.9%,平原占19.9%,水域占7.5%,中部高四周低。最高点为许孟镇境内的马耳山,海拔706m;最低点为北京路街道的东海峪村,海拔1~1.5m。日照市辖11个街道办事处、40个镇、4个乡[13]。日照市交通网络发达、经济发展迅速,但其农村居民点的分布仍然沿袭了过往较为杂乱无章的状态,难以响应当前土地集约利用的国家战略需求。因此,分析其农村居民点的破碎程度、影响因素及相应的对策建议,可以为当前新农村建设和土地整治提供重要的推动力。
1.2 数据来源与处理
该文对农村居民点进行提取时所使用的数据主要为:2016年4月的OLI遥感数据、90m数字高程数据(DEM)、日照市乡镇行政区数据以及河流、道路等基础地理数据。
首先,对Landsat8 OLI数据进行几何校正、图像融合、图像镶嵌和图像裁剪等预处理; 之后,利用监督分类法对农村居民地斑块进行提取; 最后,将提取结果导入Google Earth进行修正,提升结果精度。以上所有数据,均进行了一致性检验、坐标系转换、地理配准等预处理。
2 研究方法
居民点破碎度表征了由于自然或人为干扰所导致的居民点被分割的破碎程度,反映了居民点分布空间结构的复杂性、异质性和不连续性。其破碎程度可以反映农村居民点的规模、形状和分布情况,不同破碎程度下土地集约利用程度也不同。因此该文借鉴景观格局研究思路,从面积、形状和分布状况3个方面选取指标,构建农村居民点综合破碎度评价模型测算各乡镇的破碎度综合指数(FragmentationComprehensiveIndex,FCI),探测各乡镇农村居民点的空间分布差异。在此基础上采用多元回归模型剖析FCI的显著性影响因素,为后期新农村建设和土地整治提供决策建议。
2.1 农村居民点破碎度评价模型
2.1.1 农村居民点破碎度评价指标选取
遵循指标体系建立的科学性、目的性、完整性、可操作性等原则,并综合考虑研究区实际特征,该文综合选择5个指标表征农村居民点分布破碎化程度,以综合反映居民点破碎化分布的规模、形状和分布状况。
①平均斑块面积(MPS)。地块面积是最基本的空间特征,可以比较直观地反映居民点的破碎化程度,同时农村居民点斑块面积的大小将直接影响居民地整理模式的选择。其数值越小,破碎化程度越大。
MPS=A/N
(1)
式(1)中,A代表农村居民点斑块的总面积,N代表农村居民点斑块的总个数。
②地块密度(PD)。地块密度是居民点斑块面积破碎化的具体量化,其数值越大,破碎化程度越大。
PD=n/A
(2)
式(2)中,n代表农村居民点的数量,A代表农村居民点斑块的总面积。
③边界密度指数(ED)。边界密度指数是分析居民点斑块形状的重要指标[7],边界密度指数越大,表示居民点斑块被分割的程度越大。
ED=E/A
(3)
式(3)中,E代表农村居民点斑块的边界总长度,A代表农村居民点的总面积。
④平均形状指数(MSI)。形状指数代表居民点斑块形状的复杂程度,形状越复杂,说明农村居民点的形态越不稳定,继续扩张分化的可能性就越大,因此将形状指数作为衡量农村居民点破碎程度的指标之一。
(4)
式(4)中,a为每个农村居民点的面积,P为每个农村居民点的周长,N为农村居民点总数目。
⑤斑块数量破碎化指数(FN)。用于衡量居民点斑块分布破碎程度的指标,介于0~1之间,0代表完全没有破碎,而1代表完全破碎。
FN=(N-1)amin/A
(5)
式(5)中,A是农村居民点总面积,amin是研究单元内农村居民点斑块最小面积,N是农村居民点总数目。
2.1.2 数据标准化和指标赋权
由于各指标之间含义不同,量纲不同,利用比重法对原始数据进行标准化处理,使各指标具有统一可比性。标准化处理区分正逆指标,正向指标越大,FCI值越大,逆向指标越大,FCI值越小。
该文基于博弈论的思想确定主客观权重的最优权重值。首先利用专家打分法对系统层进行主观赋权,然后利用变异系数法对指标层进行赋权。变异系数法的基本思想是以指标之间的差异程度来确定各指标的权重[18],是一种客观赋权的方法。博弈论的思想是在不同的权重之间寻找一致或妥协,最终得到一组优化权重值。经计算,研究区农村居民点破碎度评价指标权重如表1所示。得到FCI的计算公式:
FCI=MPS×0.342 8+PD×0.182 8+ED×0.178 5+MSI×0.120 5+FN×0.175 4
(6)

表1 研究区农村居民点破碎度评价指标权重
2.2 空间自相关分析
研究分析FCI的空间自相关效应和其空间分异性。通过计算全局指数实现对FCI在整个区域的空间特征的描述,并生成LISA聚类图和Morans′s I散点图。全局Moran′s I指数可以表明具有相近FCI值的地区是否在空间上聚集,根据其值可以判断是否存在空间相关性。其计算公式为:

(7)

Moran′s I散点图和 LISA 聚类图表示局部空间上的自相关结构。Moran′s I散点图的4个象限可以反映每个乡镇FCI与其周边乡镇FCI的联系,从第一到第四象限分别是“高高”、“高低”、“低高”、“低低”。LISA聚类图则在地图上反映了通过空间关系显著性检验的这4种关系。
2.3 破碎度影响因素分析方法
2.3.1 主要影响指标选取
该文参考相关文献[6,11],并结合日照市农村居民点实际分布特征,从自然环境与社会因素两方面,选取海拔高度、坡度、地形起伏度、河流密度、距海岸线的距离、距县城的距离、道路密度共7个候选指标。其选择依据如下(见表2)。

表2 农村居民点破碎度影响指标体系
(1)海拔高度在一定程度上决定了农村居民点的发展条件,发展较快的农村居民点一般具有较高的破碎度。
(2)坡度越大,耕种难度越大,工程建设的成本也就越高,居民点的分布也就越破碎。
(3)地形起伏度代表了地形的复杂程度,地形越复杂,对农村居民点的分割作用也就越强。
(4)自古以来,河流都是人们重要的水源,为了方便生活取水,人们都是沿着河流居住,河流的存在也成为了影响农村居民地空间分布的重要因素。
(5)日照市位于沿海地区,距离海岸线越近,渔业和旅游业的经济带动作用越强,农村居民点的发展就越快。
(6)距离县城的距离的大小决定了农村居民点的区位是否优越,区位是影响农村居民点发展的重要因素。
(7)道路是农村居民点对外交流的主要通道,道路系统越发达,越有利于农村居民点的扩大和发展,同时道路对斑块还具有切割作用。
2.3.2 多元回归模型
该文采用多元回归分析方法研究FCI影响因子与FCI之间是否存在某种线性或非线性关系,以此探测分析各候选影响因子对FCI的影响程度。在采用SPSS软件分析前,利用比重法对选取的影响因子进行标准化处理。
3 结果分析
3.1 基于破碎度综合指数的农村居民点分布特征分析
3.1.1 农村居民点破碎度分布特征
根据公式(6)计算得到的各乡镇FCI,按照等间隔将日照市各乡镇划分为4个等级,划分结果如图2所示。从结果可以看出,破碎度由西北内陆地区向东南沿海地区逐步变大,形成了“阶梯状”的分布格局。
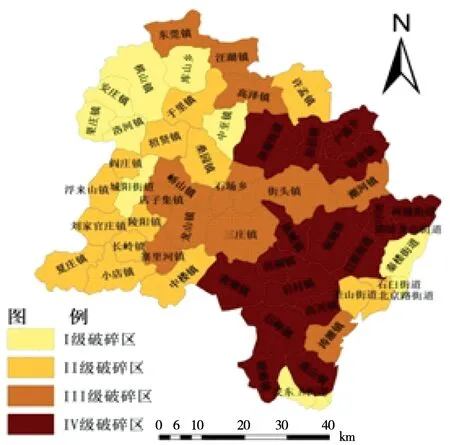
图2 研究区FCI指数分布
I级破碎区包括安庄镇、安东卫街道、棋山镇等12个乡镇。其中城阳街道、秦楼街道、岚山头街道、石臼街道、安东卫街道位于城乡结合部或处在城市范围内,表现的特征为PD值非常小; 其余的乡镇主要分布在内陆的丘陵地区,其主要特征为PD值、ED值和MSI值比较小,而平均地块面积MPS较大。Ⅱ级破碎区包括许孟镇、夏庄镇、招贤镇等14个乡镇,主要分布在莒县的平原地区。其特征是平均地块面积MPS和PD值较高,ED值和MSI值比较小。Ⅲ级破碎区包括汪湖镇、龙山镇、涛雒镇等12个乡镇,主要分布在日照市中部山区。其特征是ED值和MSI值比较高。Ⅳ级破碎区包括碑廓镇、虎山镇、日照街道等17个乡镇,主要分布在沿海平原地区和五莲县的山地丘陵区。沿海平原破碎区的特征是MPS值较小,PD值、ED值和MSI值都较大。在五莲县的山地丘陵区,ED值、MSI值和FN值比较大。

图3 Moran散点图 图4 LISA聚类图
3.1.2 空间自相关性结果分析
对FCI进行空间自相关分析,得到图3所示的Moran′s I散点图和图4所示的LISA聚类图,并采用999次随机化运算增强结果稳健性。全局Moran′s I指数为0.45,且通过显著性检验,表明FCI整体上存在显著的聚集效应。而且从图3可以看出,大部分的离散点分布在第一和第三象限,说明FCI在空间上有显著的集聚效应,即存在空间正自相关性。从图4可以看出,通过检验的高高聚集分布的乡镇共有5个乡镇,分别为:后村镇、三庄镇、高兴镇、陈疃镇、巨峰镇。大部分位于日照市的山地丘陵地区,其复杂的地形条件使得居民点分布比较零散,FCI都较高。属于低低聚集分布的乡镇共有2个,分别为:安庄镇、洛河镇。安庄镇和洛河镇分布在日照市西部的丘陵地区,以农业发展为主,农村居民点形态比较稳定,FCI较小。低高分布的有2个,分别为:许孟镇、秦楼街道。许孟镇位于鲁东低山岭与鲁中南低山丘陵衔接地带,境内虽然有海拔较高的马耳山,但主要的地形为丘陵和平原,和邻近乡镇相比,受地形的影响较小,FCI较小。秦楼街道位于城市范围内,大部分村庄已实现了“城市化”,剩余的农村居民点数量比较少,因此FCI较周边乡镇低。高低分布的只有岚山区的虎山镇,虎山镇位于岚山区南部,南邻安东卫街道,北邻涛雒镇,涛雒镇是山东省中心镇、小城镇建设示范镇,城镇化的水平较高,安东卫街道也具有较高的城镇化水平,所以FCI较低。虎山镇是沿海乡镇,境内地形以平原为主,且交通网络发达,港路区位优势十分明显,所以FCI较周围其他乡镇高。
3.2 农村居民点破碎度影响因素
3.2.1 模型结果
该文采用逐步回归的方法将变量逐个引入模型,由表3拟合过程可知,经过4步拟合完成了多元线性回归方程的建立。方程的拟合优度随着变量的逐步引入不断上升,判定系数R2从0.240增加到0.603,最终被引入的评价指标可以解释农村居民点破碎度影响因素的60.3%变差。经过对变量的筛选,表3中的第4个模型为最终的方程,被引入的变量共有4个,如表4所示。在显著性水平为α=0.1的情况下,回归方程偏F检验的概率P=0<α,F统计量比值等于17.861,说明FCI与解释变量间存在显著的线性关系,且显著性检验结果较为显著,最终的回归方程符合研究的需要。

表3 模型拟合度分析

表4 回归系数分析

表5 未通过变量分析
3.2.2 影响因素分析
对样本数据进行回归系数分析,经回归系数显著性T检验,得出模型保留变量的非标准化回归系数和标准化回归系数,如表4所示。标准化回归系数反映了各个变量对FCI大小的影响程度。
(1)影响因素距海岸线距离(X5)的显著性T检验的概率P=0<0.1,标准化回归系数β值为-0.718,统计学意义显著。研究区位于东部沿海地区,有丰富的海洋资源,依托港口和沿港工业区形成了蓝色经济区,因此海洋资源成为影响居民点形成和发展的主要原因。近海地区,原始居民以捕捞为业,在居民点选址时,会优先考虑靠近海岸的地方; 在经济发展中,旅游业的发展和蓝色经济区的战略规划使得沿海地区经济迅速发展,居民点数量不断增加,形态不稳定,处于迅速扩张的时期,所以在靠近海岸的地区,FCI较高。
(2)影响因素道路密度(X7)的显著性T检验的概率P=0.057<0.1,标准化回归系数β值为0.284,统计学意义显著。随着道路密度的增大,农村居民点的破碎度逐渐变大。在道路密度较大的地区,交通比较发达,有利于农村居民点的规模的扩大和发展,所以农村居民点的密度比较大,而且农村居民点会沿路分布和扩张,使得斑块形状复杂,边界密度变大,FCI会高于道路密度较低的地区。日照市平原地区的道路网十分密集,交通非常发达,山地丘陵区稍微欠缺,构成了四通八达的交通网络,密集的交通网络对斑块也会有一定的切割作用,同样也会加剧农村居民点的破碎程度。
(3)影响因素距县城的距离(X6)的显著性T检验的概率P=0<0.1,标准化回归系数β值为-0.412,统计学意义显著。距县城的距离对农村居民点的破碎度有显著的影响,距县城越近,区位优势越明显,受到城市发展的带动和影响就会越大,农村居民点的密度较大,同时居民点处于快速扩张的状态,所以FCI会较高。
(4)影响因素坡度(X2)的显著性T检验的概率P=0.016<0.1,标准化回归系数β值为0.316,统计学意义显著。FCI受到坡度的影响,坡度越大,居民点的分布越分散,破碎度越大。这是因为农村以农业生产活动为主,耕地一般分布在平原、山间谷地,为了方便生产,居住地选在耕地附近,坡度越大,耕种难度越大,同时,工程建设成本越高,水土流失、滑坡等问题越严重,不利于农村居民点的形成和发展,农村居民点的面积较小、形状不规则。
(5)未通过模型筛选的变量为地形起伏度(X3)、距河流距离(X4)、海拔高度(X1),变量的显著性T检验的概率均大于0.1,且其标准化系数分别为-0.181、0.071、-0.119,统计学意义不显著。海拔高度属于地形地貌因素,在数量上进行分析,农村居民点主要分布在0~200m的高度范围内,在大于200m时分布数量较少,所以影响效果并不显著。在研究区内,只有5条较大的河流,数量较少,对FCI没有显著影响。地形起伏度(X3)和海拔高度(X1)的VIF分别为16.393,11.364,具有较高的共线性,对农村居民点破碎度的影响不显著。
4 结论与政策建议
该文通过构建乡镇级农村居民点破碎度评价模型,测算研究区55个乡镇的FCI值,FCI由西北向东南逐渐变大,内陆地区破碎度低,沿海地区破碎度高,地区间破碎程度差异较大,形成了“阶梯状”的空间分布格局。利用多元回归模型分析了显著性影响因素,对FCI有显著影响的指标有4个,根据影响程度大小排列依次为:距海岸线的距离(X5)、距县城的距离(X7)、坡度(X6)、道路密度(X2)。根据上述居民点分布特征及影响因素探测结果,再结合研究区的人文、经济、资源和区位等条件,设计并开展因地制宜的土地整治模式。
I级破碎区中北京路街道、秦楼街道、安东卫街道位于城乡结合部或处在城市范围内,比较适合社区化整理模式。该部分居民点距海岸线较近,且道路密度大,其居民点扩张、FCI变大的可能性较高,所以应做好合理的规划和预防措施,同时该部分农村居民点区位条件较好,经济发展水平高,城镇化趋势显著,将农村居民点整理和城镇规划衔接是最适合的方法。其余的乡镇主要分布在低山丘陵地区,距离海岸线和县城较远,所以经济发展慢,而且部分村庄规模较大,基础设施不完善,存在大量闲置宅基地,空心村现象比较严重,在居民点整理中不适合整村搬迁模式,可以考虑采用村内整理模式,完善村庄配套基础设施,保障每户通电、通水、通路,控制村庄规模,提高土地利用率。
Ⅱ级破碎区的农村居民点虽然位于平原地区,但其经济水平较低,以农业为主,所以比较适合资金需求较小的村内整理模式。该部分农村居民点的面积比较大,村内土地利用粗放、闲置率高,应鼓励优先使用旧宅基地和空闲地建房,并将多余的土地统一规划,优先复垦发展农业。
Ⅲ级破碎区的农村居民点主要分布在山地丘陵地区,FCI受坡度的影响较大,由于地形分割形成了布局零散、规模较小、形状不规则的现状。其自然环境恶劣、规模小、交通不便、基础设施条件差,在农村居民点整理中,可以考虑异地迁移模式,这种模式适合这种破碎度较高的偏远山区的村庄,而且生态效果显著,但是这种模式资金需求较大,推进速度也比较慢。
Ⅳ级破碎区主要分布在两个区域,沿海平原地区距海岸线距离近,道路密度较高,区位优势明显,经济发展较快,农村居民点的规模正在逐步扩大,FCI处于较高的水平,土地利用存在严重的问题。在农村居民点的整理中,对于面积较大的农村居民点可以采用村内整理的模式,严格执行宅基地审批制度,防止村庄向外发展扩张。对于面积较小、密度较大的地区可以采用中心村的建设模式,通过建设中心村,既能够补充耕地,又可以提高土地利用率,优化村镇布局,发挥中心村镇的规模效益和集聚功能,同时益于集中建设公共基础服务设施,加强农村管理。但是资金需求比较大,推进速度比较缓慢。在山地丘陵区,可以考虑异地迁移模式,将比较偏远的贫困村庄迁移到发展较好的地区。
通过分析不同等级破碎度的分布特征及其影响因素,给出了居民点整理模式的针对性建议,为解决土地利用问题和开展农村居民点整理提供了可靠的依据。由于数据获取的限制,缺少村级居民点行政边界,导致研究尺度不够精细,且缺少时空演变分析。构建的农村居民点综合破碎度评价模型还需进一步改进,对部分重要指标可能存有遗漏。后续研究中将加强这方面的研究,结合新农村建设的需要,在村级尺度下对农村居民点的破碎度进行分析。
