基于随机森林MOPSO的城市最优资本结构分析

李燕燕， 杨昊天， 曾玙璠

(1.郑州大学 商学院，河南 郑州 450001； 2.郑州大学 产业技术研究院 电气工程学院，河南 郑州 450001； 3.英国利物浦大学 数学科学系,利物浦)

0 引言

城市作为国家经济增长最有力的支撑，也是各种资本最活跃的空间区域，各种经济问题在城市的平台上表现得最为直接.进入新常态，出现了动能困境、结构失衡、脱实就虚、公共服务产品短缺等一系列问题，这些问题的背后其实是资本规模大小的市场配置状况.随着城镇化进程的深入，城市的资本化程度也越来越高，所谓的城市资本化是使纳入城市的资产以货币化形式进行运作，是土地资本、金融资本、产业资本、科技资本(含人力资本)以及公共服务资本等高度耦合健康循环发展的模式.

目前理论界关于城市资本的研究多是从单个资本的视角来研究，诸如土地财政与城市发展、金融资本与经济增长、金融促进产业发展等,关于多重资本结构配置的研究相对较少.城市资本结构是一个受到多目标多因素交互影响的复杂问题，单一工具很难对此做出较为全面的解释.城市资本所涉及的土地资本、金融资本、产业资本、科技资本以及公共服务资本虽有各自的运行特征和规律，其作用机制和强度具有一定差别，但它们之间并非互相割裂，而是互相影响、互动耦合发生作用.所以，笔者选取30个省级行政中心(拉萨除外)为代表，基于2002～2016年各城市地区生产总值、人均地区生产总值、全社会固定资产投资、土地出让金、第二产业增加值、规模以上工业企业利润总额、第三产业增加值、金融增加值、科教支出(科技支出和教育支出)、年末总人口数、城镇单位从业人员期末人数、城镇居民人均可支配收入、职工平均工资、当年实际利用外资金额等数据，透视土地资本、金融资本、产业资本、科技资本以及公共服务资本的作用特征，通过利用随机森林算法从多维角度考察城市资本结构的复杂关系，采用多目标粒子群约束优化算法构建多目标多因素影响下的城市最优资本结构模型，了解城市资本结构配置的状况以及相互作用的对冲效应，寻找最接近目标模式的年份和城市，为城市资本内部结构调整和功能提升提供参考价值．

1 相关算法

1.1 随机森林

随机森林回归(random forest regression，RFR)算法是Breiman等[1]于2001年提出的.该算法将Bagging集成学习理论与随机子空间方法结合[2]，是一种基于决策树的集成学习算法.

随机算法不但能够处理连续的数据问题，而且也可以处理具有离散属性的数据，其运行速度快，且稳健性和抗噪性强，所以该算法被广泛应用于生物信息领域基因序列的分类和回归等[3-4]、经济金融领域客户信用分析及反欺诈等[5-6]以及数据挖掘领域异常检测和度量学习等[7-8]方面.

为了能够提高模型精度并避免出现过拟合的情况，随机森林算法引入了Bagging和随机子空间思想[9].笔者通过评价模型的拟合效果和检验模型预测结果来评价模型的预测能力，通过计算RFR模型的决定系数(R2)和均方根误差(RMSE)来评价模型的拟合效果[9].

1.2 粒子群优化算法

由于粒子群优化算法(particle swarm optimization)[10]具有编程简单、直观易实现等优点，所以在工程上得到了广泛的应用.粒子群优化算法的思路：初始化种群规模设置随机为N，粒子群的维度设置为D，迭代次数为k时，xi=(xi,1,xi,2,…,xi,D)作为第i个粒子的位置，此时这个粒子通过向它的个体极值pbesti和全局极值gbest学习来更新它的位置，之后在迭代过程中不断计算每次粒子的个体极值和全局极值.如果此代极值比上一代极值好，那么就将这代极值更新，反之则保留上一代的个体极值和全局极值.接下来，判断粒子群算法是否达到设置的停止条件，若达到则将最优解输出，反之将继续迭代，更新粒子的速度和位置.经过不断地迭代更新后，最优解最终会出现.粒子群的速度更新如式(1)和位置更新如公式(2).

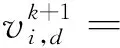
(1)

(2)

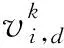
1.3 多目标粒子群约束算法

一般情况下，多目标优化问题的各个子目标是相互冲突的，一个子目标的改善有可能会引起另一个子目标的降低，同时使多个子目标一起达到最优值是不可能的，只能在它们中间进行协调和折中处理，使各个子目标都尽可能地达到最优化.与标准的粒子群算法的流程大体一致[11-12]，流程参照文献[13].

粒子群算法已经在多领域得到应用，如云计算领域的云计算消耗源调度问题[14]，电力系统领域用于电力系统的经济可靠运行[15-16],解决电力系统经济调度等问题[17]，经济领域用于解决最大利益的股票交易决策多目标优化等问题[18]，数据挖掘领域应用于多目标数据分类规则挖掘以及对数据集进行分类规则挖掘等[19].

2 随机森林多目标粒子群算法

2.1 算法结构

随机森林算法是集成算法，能够对数据实现快速高度拟合.随机森林算法可以利用决定系数(R2)和均方根误差(RMSE)得出数据特征与目标特征之间的关系.当然，此时特征与目标特征之间的关系并不能用具体的函数表达式表示，而是利用随机森林算法通过训练数据训练出来的模型来表示特征与目标特征之间的关系.通过这样的方式，就可以利用随机森林模型作为多目标粒子群算法的目标函数.因为利用多目标粒子群算法寻优需要使得多个目标同时达到最优,所以使用随机森林模型构建出各个目标特征与其他特征之间的关系作为目标函数.考虑到在实际应用中各个特征必然存在一定的约束条件，所以在使用多目标粒子群算法寻优之前，需要对各个特征添加约束条件.当粒子超过边界时，则重新随机进行初始化.用这样的结合方式，既可以利用随机森林的拟合特性将数据特征与所选目标特征进行高度拟合得出其关系，又可以根据多目标粒子群算法进行寻优，找到能够同时达到多目标的最优点.

2.2 算法应用

此次研究的目标是寻找城市最优资本结构.设定人均地区生产总值和城镇居民可支配收入同时达到最高时所对应的各个特征值为城市资本结构配置最优的条件.在进行多目标优化时，需要明确多目标的特征值与其他特征值之间的关系.基于所分析的数据逻辑关系复杂，计算量大，使用随机森林算法可以快速、准确、高效地从复杂的数据中提取出多目标特征与其他特征值之间的关系，而粒子群算法是目前传统又经典的寻优算法之一，将各个数据特征根据实际情况进行条件约束，随后利用多目标粒子群约束优化算法进行寻优.多目标粒子群约束优化算法与随机森林相结合的随机森林多目标粒子群算法，既能快速高效地得出合理方案，又减少了算法的复杂性.利用该算法可以求得最优时各个特征的值即为城市最优资本结构，然后根据30个城市2002～2016年间数据与城市最优资本结构的相关性，得出资本结构配置相对较优的城市及年份.

3 实证检验

3.1 数据分析

表1中列出本次试验数据所选取的城市、城市类别、数据年份区间、数据所用到的特征以及目标特征.其中，城市类别1代表一线城市；类别2代表新一线城市；类别3代表二线城市；类别4代表三线城市；特征表示实验中选择城市的特征值；目标特征表示本次研究所选取的目标方向.

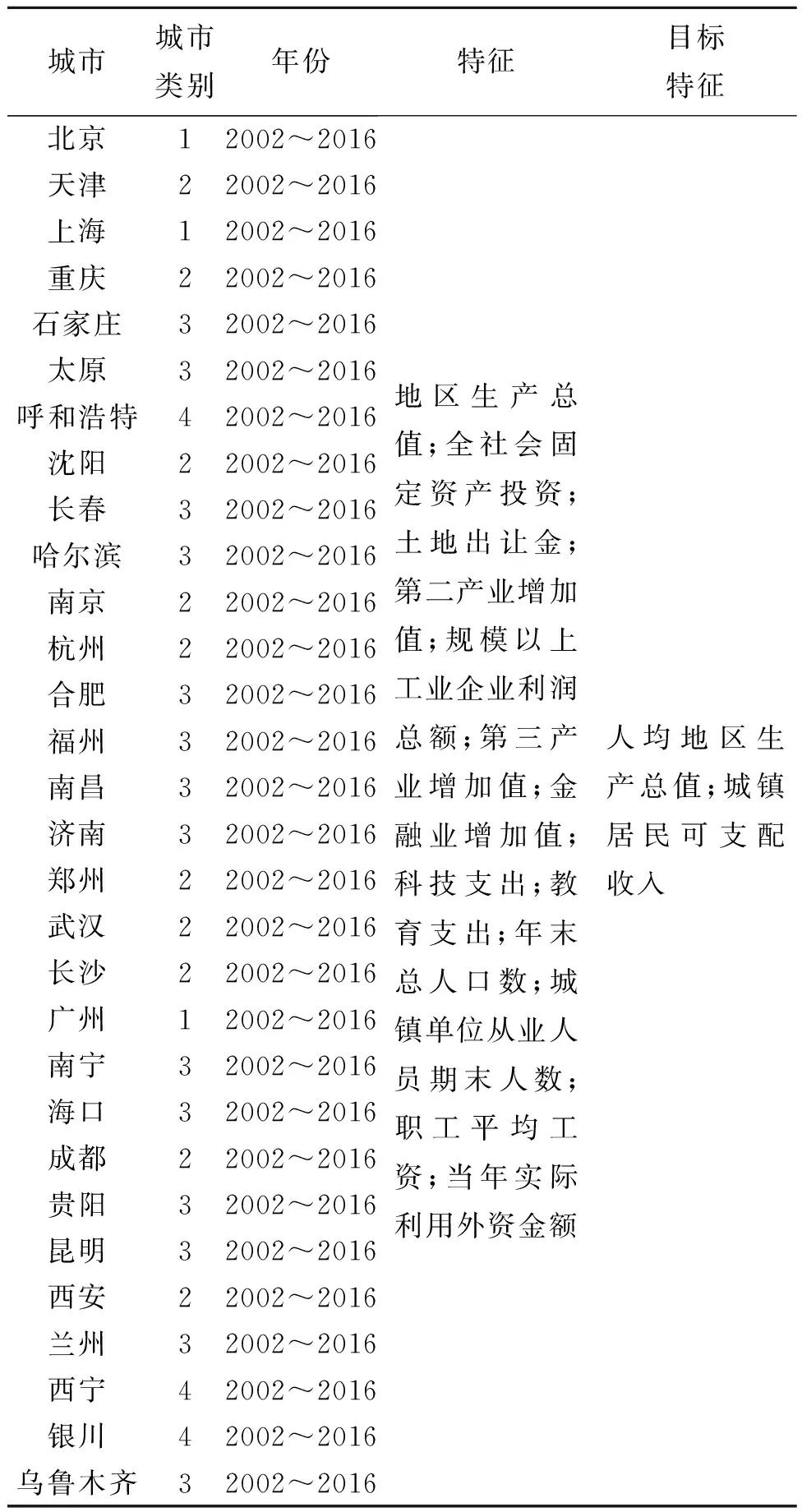
表1 实验所选数据的结构Tab.1 The structure of data selected for the experiment

由于需要对特征之间的关系进行研究，所以实验选用两个特征作为目标，用随机森林进行拟合并求得这两个特征与其他特征之间的关系.

3.2 算法参数选择

目前面临的任务属于多特征的数据，因此为了进行复杂程度较高的拟合方式，参数需要进行一定程度的调整.随机森林中，选择随机个数为10个，选择迭代次数为1 000次，所选择算法的最大函数评价次数均设置为240 000.粒子群优化算法的参数设置：种群规模为50，惯性权重w随着迭代次数从0.9至0.4线性递减，学习因子c1与c2均为1.494 45，r1与r2每次迭代随机取0～1的任意数.

3.3 拟合效果评价

关于拟合效果如何，根据模型的决定系数(R2)和均方根误差(RMSE)来评价模型.利用随机森林模型拟合之后得出决定系数(R2)和均方根误差(RMSE)分别为0.995 6和0.000 45.结果发现，随机森林模型可以实现高度的拟合.在对历史数据进行高度拟合之后，可以得出历史各个特征与目标特征之间的关系.

3.4 结果分析

通过拟合效果的评价，可知随机森林模型可以实现与历史数据的高度吻合，能够准确地代表历史中目标特征与各个特征之间的关系.在此基础上，利用多目标粒子群约束算法寻找多个目标特征最优化时所对应的各个特征之间的确定值.利用相关性函数式(2)，求出最优的解集与历史数据的相关性系数，可以得出最优解，即设定的年份期间中最优的城市资本结构.

(2)

式中：Cov(X，Y)为X与Y的协方差；Var[X]为X的方差；Var[Y]为Y的方差.

鉴于中国地区差异，依据第一财经新一线城市研究所对338个地级以上城市的排名，将城市分为一线城市、新一线城市、二线城市、三线城市.其中，笔者所选用的30个城市中，一线城市有北京、广州、上海；新一线城市有成都、杭州、济南、昆明、南京、沈阳、天津、武汉、西安、长沙、郑州、重庆；二线城市有福州、贵阳、哈尔滨、海口、合肥、兰州、南昌、南宁、石家庄、太原、乌鲁木齐、长春；三线城市有呼和浩特、西宁、银川[20].

3.4.1 数据为真值的结果分析

当所有的数据使用真值进行实验时，依次选用2002～2016年间全国的30个城市以及30个城市中的一线城市、新一线城市、二线城市、三线城市的数据进行实验.这里用热力图表示实验结果，颜色越深代表相关性越高，城市资本结构配置越好；颜色越浅则相关性越低，城市资本结构配置越差.

2002～2016年间全国30个城市中，城市资本结构配置最好的是2007年西安市，相关系数为0.994 787；其次是2009年的合肥市，相关系数为0.993 822；再次为2002年的成都市，相关系数为0.990 588.将各个城市15 a综合起来分析，全国30个城市中，城市资本结构配置最好的是西安市，相关系数之和为14.812 322；其次是南宁市, 相关系数之和为14.765 423；再次为合肥市，相关系数之和为14.761 251.样本城市中的一线城市资本结构配置最好的是2002年的广州市，相关系数为0.994 057；其次为2002年的上海市,相关系数为0.993 213；再次为2004年的北京市，相关系数为0.992 688.将各个城市15 a综合起来分析，样本城市中一线城市中城市资本结构配置最好的是广州市，相关系数之和为14.840 293；其次为北京市, 相关系数之和为14.820 292；再次为上海市，相关系数之和为14.799 533.

2002～2016年间样本城市中的新一线城市中城市资本结构配置最好的是2011年的沈阳市，相关系数为0.995 032；其次为2012年的西安市，相关系数为0.994 559；再次为2015年的济南市，相关系数为0.993 296.将各个城市在2002～2016年共15 a综合起来分析，样本城市中新一线城市中城市资本结构配置最好的是济南市，相关系数之和为14.771 292；其次为重庆市，相关系数之和为14.763 693；再次为沈阳市，相关系数之和为14.760 872.

2002～2016年样本城市中的二线城市中城市资本结构配置最好的是2002年福州市，相关系数为0.998 697；其次为2015年的太原市，相关系数为0.998 690；再次为2009年的南昌市，相关系数为0.998 664.将各个城市在2002～2016年15 a综合起来分析，二线城市中城市资本结构配置最好的是海口市，相关系数之和为14.950 136；其次为南昌市，相关系数之和为14.950 021；再次为南宁市，相关系数之和为14.948 310.

2002～2016年样本城市中的三线城市资本结构配置最好的是2004年银川市，相关系数为0.999 594；其次为2006年西宁市，相关系数为0.998 408；再次为2006年呼和浩特市，相关系数为0.998 250.将各城市15 a综合起来分析，三线城市资本结构配置最好的是银川市，相关系数之和为14.973 522；其次为西宁市，相关系数之和为14.969 383；再次为呼和浩特市，相关系数之和为14.968 272.

综上所述，通过多目标粒子群算法得出的最终结果作为最优城市资本结构配置.表2展示了所选数据为真值时，得出的与标准模式最接近的年份城市以及15 a综合分析最接近标准的城市.

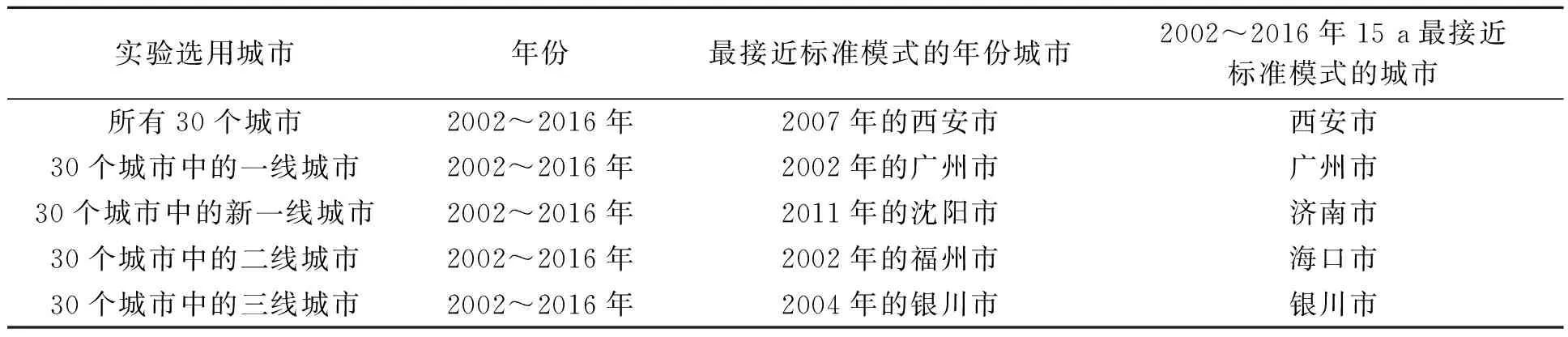
表2 数据为真值的实验结果Tab.2 The experimental result of the data being true

3.4.2 数据为增长率的结果分析

将所有的数据使用增长率时再次进行实验，仍旧依次选用2002～2016年15 a全国30个城市和30个城市中的一线城市、新一线城市、二线城市、三线城市的数据进行实验.

2002～2016年间样本城市中城市资本结构配置最好的是2005年的北京市，相关系数为0.992 001；其次为2011年天津市，相关系数为0.987 330；再次为2002年的济南市，相关系数为0.982 865.将各个城市15 a综合起来分析，样本城市中城市资本结构配置最好的是上海市，相关系数之和为14.553 823；其次为武汉市，相关系数之和为14.538 332；再次为北京市，相关系数之和为14.489 001.

2002～2016年间一线城市资本结构配置最好的是2016年的上海市，相关系数为0.675 601；其次为2011年的广州市，相关系数为0.606 031；再次为2006年的北京市，相关系数为0.536 633.将各个城市15 a综合起来分析，样本城市中一线城市资本结构配置最好的是北京市，相关系数之和为3.205 879；其次为广州市，相关系数之和为2.792 489；再次为上海市，相关系数之和为2.679 620.

2002～2016年间样本城市中的新一线城市资本结构配置最好的是2011年的长沙市，相关系数为0.802 936；其次为2006年的重庆市，相关系数为0.767 792；再次为2004年的西安市，相关系数为0.749 976.将各个城市15 a综合起来分析，样本城市中新一线城市中城市资本结构配置最好的是长沙市，相关系数之和为3.668 056；其次为西安市，相关系数之和为2.916 951；再次为济南市，相关系数之和为2.760 118.

2002～2016年间样本城市中的二线城市资本结构配置最好的是2003年的长春市，相关系数为0.785 886；其次为2007年的南昌市，相关系数为0.677 504；再次为2002年的福州市，相关系数为0.667 149.将各个城市15 a综合起来分析，样本城市中二线城市资本结构配置最好的是长春市，相关系数之和为6.350 041；其次为福州市，相关系数之和为4.654 140；再次为太原市，相关系数之和为4.347 684.

2002～2016年间样本城市中的三线城市资本结构配置最好的是2011年西宁市，相关系数为0.700 435；其次为2010年呼和浩特市，相关系数为0.577 654；再次为2006年银川市，相关系数为0.560 824.将各城市15 a综合起来分析，样本城市中三线城市资本结构配置最好的是西宁市，相关系数之和为2.057 544；其次为呼和浩特市，相关系数之和为1.978 628；再次为银川市，相关系数之和为1.302 793.

综上所述，通过多目标粒子群算法得出的最终结果作为最优城市资本结构配置.表3展示了当所选数据为增长率时，得出的与标准模式最接近的年份城市和15 a综合分析最接近标准模式的城市.

表3 数据为增长率的实验结果Tab.3 The experimental result of the data being growth rate

4 结论

笔者将人均地区生产总值和城镇居民可支配收入同时达到最高时所对应的各个特征值为城市资本结构配置最优的条件，然后用真值数据和增长率数据分别将城市按照一线、新一线、二线、三线4类进行划分后，逐一分析计算出各个类型中最优资源配置的年份和城市.无论是用真值还是增长率实验的结果，除了2016年的上海市之外，其余得出的最优年份城市均在2002～2011年之间，这期间恰恰是中国经济持续快速发展的十年，2007年中国GDP增速最高，达到14.2%.用增长率实验的最优年份城市是2005年的北京市，用真值实验的最优年份城市是2007年的西安市，而西安市属于西北地区省会城市，相对发达地区发展要滞后一些，其城市资本结构在全国增速最高的年份趋于最优也是合理的.用真值实验的15 a最接近标准模式的城市仍是西安市，用增长率实验的15 a最接近标准模式的城市则是上海市.此外，需要关注的城市是长沙市，不仅在2011年最接近标准模式，而且也是15 a最接近标准模式的城市.后续的研究需要进一步针对不同城市不同发展阶段深入分析其资本结构的变化，为城市资本结构优化配置提供更科学的参考依据.