基于鸽群优化算法的图像分割方法研究

胡春鹤， 王依帆， 朱书豪， 刘文定

(北京林业大学 工学院，北京 100083)

0 引言

图像分割技术将图像分割成若干个具有独特性质的区域，并从中提取出所需目标，是当前图像分析和识别技术的研究热点，被广泛应用于多个领域，如机器视觉[1]、交通控制[2]、卫星定位物体[3]、病虫害监测[4]等.

图像分割技术属于典型的分类问题，依照不同的分类准则，主要分为阈值分割[5]、区域分割[6]、边缘分割[7]等.由于阈值分割相较于其他方法具有简单、易实现的特点，使其成为图像分割领域应用最为广泛的一类方法[8].图像阈值分割法根据提取目标与背景在像素灰度上的差距，利用单一或多个阈值对像素点灰度进行逐一比较实现分割[9].该方法分割效果优劣的关键在于最优阈值的选择，这通常需要求解含有多种约束条件的非线性优化问题.由于非线性优化方程的梯度难以求解，使得现有求解过程复杂且耗费大量运算时间[10].

仿生群体智能优化算法因其能够有效处理非线性优化问题，同时具有收敛速度快等特点而受到广泛关注.利用此类方法解决图像分割算法问题已成为这一领域的研究热点.仿生群体智能优化算法是一类通过模拟自然界生物群体，如蚁群[11]、狼群[12]等群体行为而产生的随机搜索与优化算法.利用上述方法解决图像分割问题，仍然存在着收敛速度慢、优化结果易陷入局部最优等问题.近年来，一种受鸽子归巢行为启发而产生的鸽群优化算法(pigeon-inspired optimization,PIO)在群体智能优化领域逐渐取得关注[13].该算法相较于一般仿生优化算法具有结果最优性、快速收敛性以及参数量适中等显著优势，被广泛用于解决无人机编队[14]、控制参数优化[15]等多个领域.显然，笔者开展的适应于图像分割的PIO算法对该领域具有重要意义.

PIO算法以最大间类方差为优化目标，以像素概率分布有限为约束条件，将图像分割问题建模为一类有约束的非线性优化问题，修改PIO优化算法对该优化问题实现求解获得最优阈值，根据所得最优阈值实现图像分割[16].进一步与现有粒子群优化算法(particle swarm optimization,PSO)[17]、KSW[18]等图像分割方法对比，验证本文方法的有效性.

1 问题描述

图像前景与背景通常存在一定的灰度差异，若能找到区分上述差异的最优灰度阈值，则可通过对比各像素点灰度值与最优阈值进行像素点二值化，即可实现分类，从而达到分割的目的.

假定给定的原始图像的灰度直方图包含L个灰度等级，设rk为第k个灰度等级，nk是在rk灰度等级上的像素点，N为总的像素点数，L为图像的灰度值，则可以得出原始图像的灰度概率分布函数满足：

(1)

采用直方图均衡化处理，可以使得图像清晰度增加，即增加背景与前景的对比度.其实现通过式(1)所示累积分布函数P(rk)得到式(2)和式(3)所示图像的原始灰度分布C(rk)和增强后灰度值Sk，达到图像增强的目的：

(2)

Sk=(L-1)·C(rk),(0≤rk≤1).

(3)

根据像素点分布概率，若选取k作为阈值，则图像将会被分割为大于和小于k的两部分，这两类像素点在图像中的概率分别为：

(4)

(5)

式中：w是第一类像素点的概率；u是第二类像素点的概率，那么上述两类像素点的内部方差为：

(6)

(7)

式中：pi(·)为每点为该类像素点的概率；u0、u1分别为第一类、第二类像素点的均值.

实现最优图像分割的优化目标函数为：

A=maxδw2(K)，

(8)

其中，δw2为各类间方差，其计算公式为：

δw2=w0w1(u1-u0)2.

(9)

当两类的类间方差最大时所取得自变量的值即为最优阈值，从而可根据此阈值得到图像分割的结果.

考虑到图像分割过程中，所提取的目标图像面积可以通过人眼目测、手动尺寸测量或者其他的方法粗略地测出来从而得到了两类像素点在图像中概率的范围，将其作为约束条件，则有：

α≤w0≤β，

(10)

λ≤w1≤γ.

(11)

2 基于鸽群优化的图像分割算法

2.1 鸽群优化算法

鸽群优化算法是根据鸽群归巢的群体特性而建立的一类仿生优化方法.当鸽群距离巢穴较远时主要采用磁场辅助导航，具有全局最优特性，而当临近目的地的时候则主要根据地标导航，具有局部快速收敛特性.通过将鸽巢视作优化目标，鸽群视作优化变量，则在距离最优值较远时采用“磁场”全局优化，用于提高寻找全局最优适应度点的速度；当临近优化值较近时采用“地标”交互优化，加快收敛速度.

在鸽群模型中，由于鸽群位于磁场中，所以鸽群中每一个成员的位置以及速度都会受到磁场的影响.鸽子飞行的过程中位置和速度会持续更新.对于给定优化目标，上述位置与速度分别代表着优化变量与优化方向.当算法开始时，每一点按照初始速度从初始位置出发，向拥有最优适应度的点收敛，到一定程度时，此类迭代停止，之后就需要引入地标模型.

当磁场模型的迭代结束后，位置的主要影响因素就变成了地标和磁场,这时鸽子飞行时就需要加大鸽群内部的资源共享，从而提高收敛速度.通过引入鸽群的中心位置来表征鸽群内部的信息交换以及资源共享.

2.2 图像分割算法

针对最优灰度阈值的寻找问题，采用上述鸽群算法来求解.磁场模型以及地标模型保证图像分割过程中每次优化迭代向着最优分割阈值收敛.假定鸽子飞行的过程中位置和速度根据式(12)～(13)进行迭代持续更新：

Vi(t)=Vi(t-1)·e-Rt+rand·(Xg-Xi(t-1))；

(12)

Xi(t)=Xi(t-1)+Vi(t)，

(13)

式中：Xi(t)和Vi(t)分别表示鸽群中第i只鸽子的位置以及单位时间内位置的变化量；R为磁场因子；Xg则为鸽群中位置最好的鸽子所在的位置，通过比较鸽群中所有鸽子的位置所对应的最优值；rand∈(0,1)是随机数.

假定鸽群中鸽子的总数为M，则鸽群中心位置Xc满足：

(14)

在有限次迭代后，鸽群位置临近目的点时鸽子位置变更为：

Xi(t)=Xi(t-1)·e-Rt+rand·(Xg-Xc).

(15)

基于对于全局收敛速度以及局部搜索速度的综合考虑，假定R迭代次数满足下式：

(16)

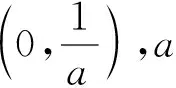
2.3 算法流程

笔者提出的基于鸽群优化算法图像阈值分割算法的具体步骤如下.

步骤1 确定初始的位置X0，鸽子总数G，两种概率的最大值w0max、w1max，最小值w0min、w1min，初始速度V0，总的迭代次数N以及磁场模型的迭代次数N0.

步骤2 计算两类像素点的概率w0、w1，两类点的均值δ02、δ12，两类间方差δw2(k).

步骤3 计算得到每点的适应度f(x).

步骤4 将该点的f(x)与该点的历史最佳位置pbest(i,t)的f(pbest(i,t))相对比，取较大者作为该点的历史最佳位置.

步骤5 将该点的f(x)与全局的最优位置Xg(t)的f(Xg(t))相对比，取较大者作为当前全局最优位置.

步骤6 在前N0代的迭代中，使用式(12)和式(13)来进行更新点的速度和位置；在迭代N0代后使用式(15)来进行位置的更新.

步骤7 重复步骤2～步骤6，直到迭代第N代后，迭代停止，输出经过图像分割处理后的图像，得到使得类间方差最大的k，将其作为阈值.

步骤8 将大于阈值的点分出来放到一幅图像中，即完成图像分割，输出分割得到的图像.

3 实验结果与对比分析

3.1 实验环境

为测试PIO优化算法对图像的分割性能，以图1(a)所示Lena、图1(b)所示Enamel和图1(c)所示car作为测试对象进行分割实验，随后分别采用粒子群优化算法(PSO)、KSW图像分割算法与本文方法进行对比测试.本文的实验硬件平台为Intel 2.4 GHz CPU，内存4 GB，仿真环境为MATLAB 2014，图像大小为256×256.

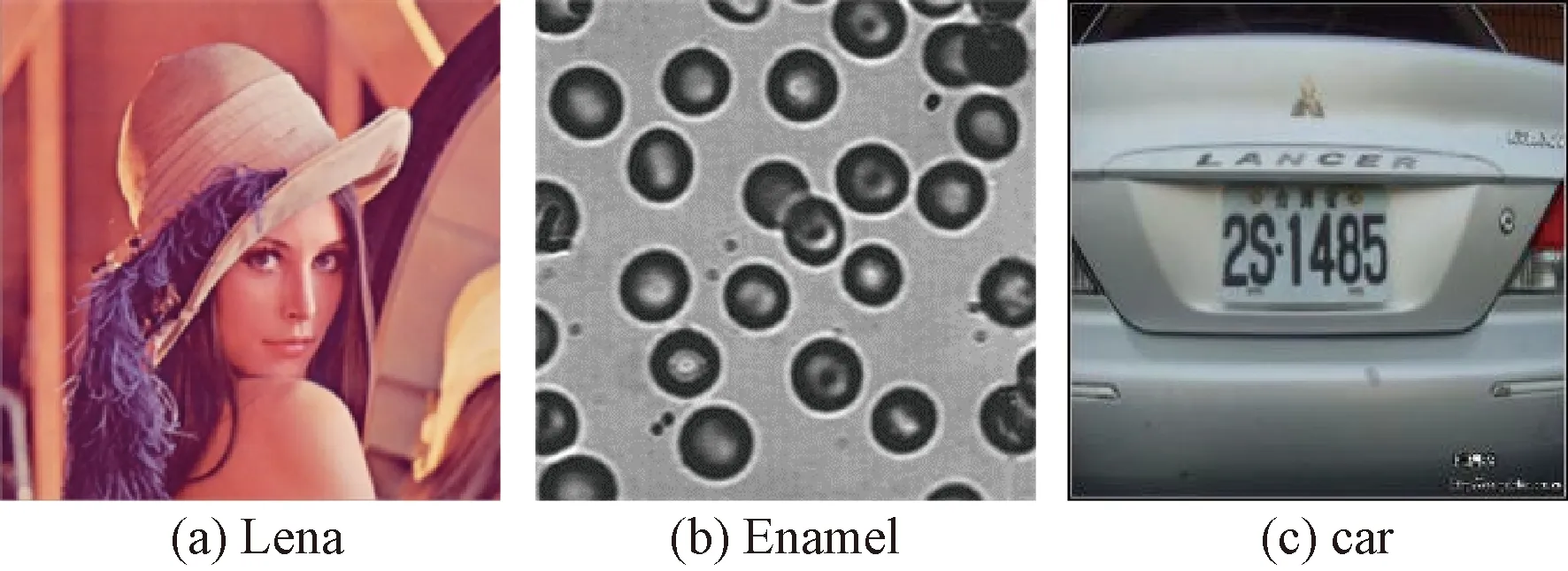
图1 典型测试图像Fig.1 Typical image for test

测试中所有算法使用的个体总群数均为20，迭代次数均为100，磁场因子R为0.3.本文算法中N代表总的迭代次数，N0代表当接近优化值采用“地标”交互优化时的迭代次数，值由式(17)进行确定.为体现结果的精确性和高效性，选取时间t和重叠度IOU(式(18))作为实验评判标准.IOU为候选框area(G)与原标记框area(C)的交集与并集的比值，即本文中分割图像与原图像的交集与并集的比值.重叠度越高，图像分割效果越好.

N0=N-N×5%.

(17)

(18)

3.2 结果分析

分别用3种不同的算法对图像进行分割，为了提高结果的准确性，使用3种不同的算法对3张具有代表性的图片进行了100次处理，得到了每次的处理时间，并分别与原灰度图像进行重叠度分析，结果如图2～4所示.可以明显看出，KSW算法分割阈值界限模糊，导致分割效果差，前景与背景有所融合，PIO与PSO算法切割效果清晰，从图中所标区域看到PIO算法细节切割更为精确，重叠度更高.

图2 KSW分割结果Fig.2 KSW split result

图3 PSO分割结果Fig.3 PSO split result

图4 PIO分割结果Fig.4 PIO split result

图2～4对比分析，KSW算法未将图像与背景完全分割出来；再将PIO算法分割图像与PSO算法分割图像进一步进行细节对比，在标红圈部分可以看到，PIO算法分割效果精确性更高，图像与背景分割明显.

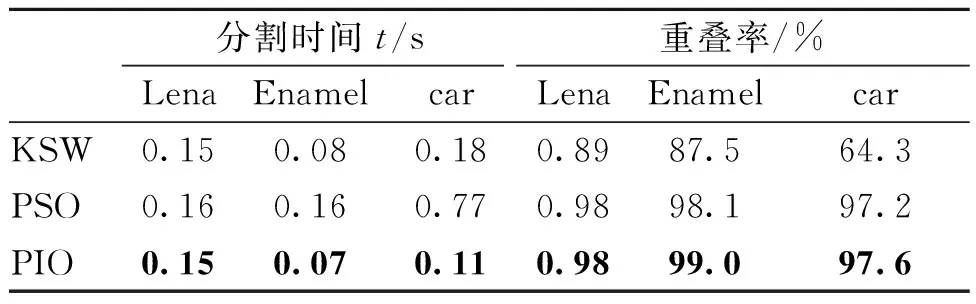
表1 各图像对应不同算法的分割时间和重叠率 Tab.1 Segmentation time and overlap of different image segmentation algorithms

为了避免随机性，笔者采用箱式图统计并对比3种算法的分割结果.

图5 Lena的算法统计结果Fig.5 Lena’s algorithmic statistics

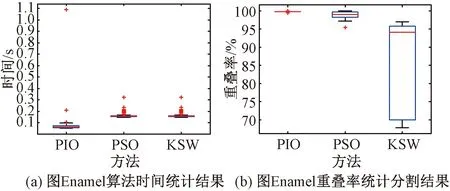
图6 Enamel的算法统计结果Fig.6 Enamel’s algorithmic statistics

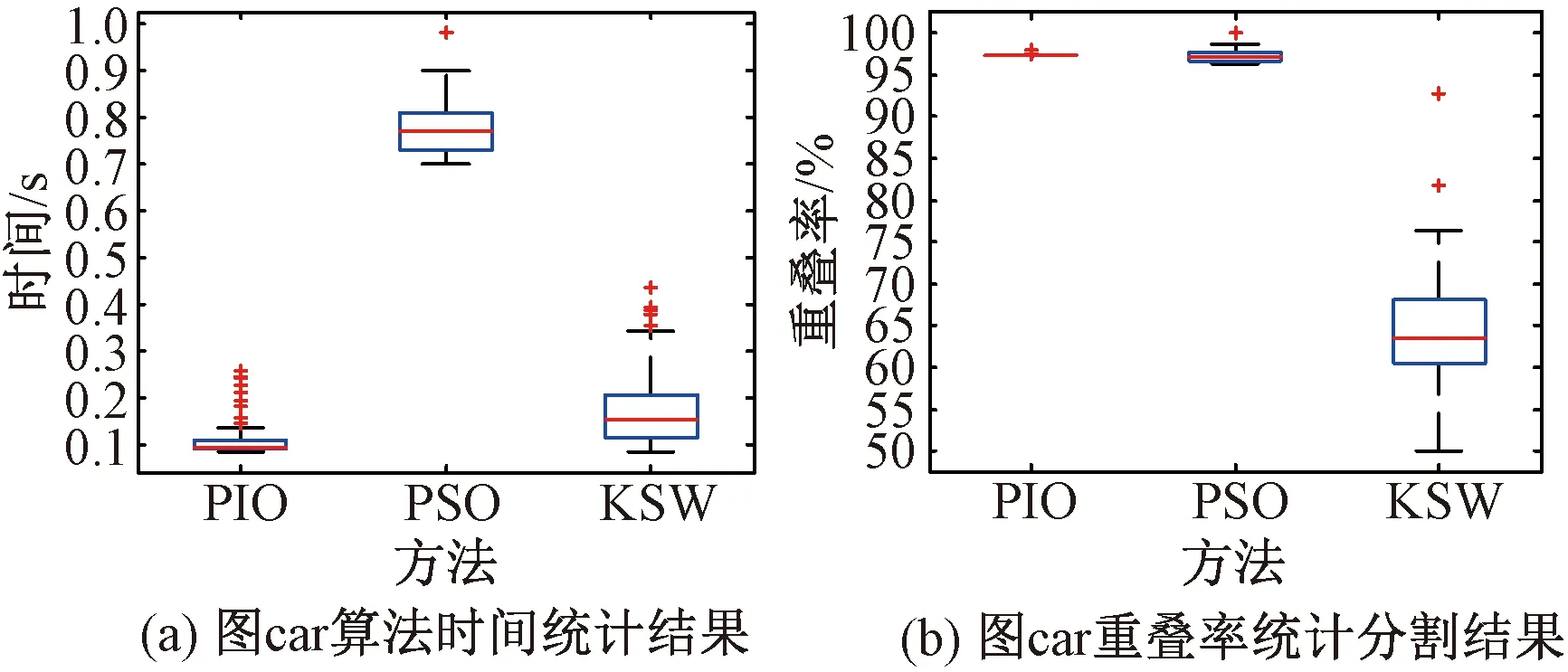
图7 car的算法统计结果Fig.7 Car’s algorithmic statistics

分割时间上，PSO效率较低，PIO和KSW更占据优势.进而得到以下结论：

(1)KSW算法分割结果前景与背景有所融合，对比不显著，图像分割清晰度不够，且在多次实验中分割结果差别较大，可看出算法稳定性不足，在重叠度上也可以明显看出，该算法较PIO和PSO分割效果不理想.

(2)相较于KSW算法，PSO算法和PIO算法有显著改善，两算法重叠度均高达0.90，在处理结果上具有较好效果，这主要是由于仿生智能优化算法具有较强的鲁棒性和搜索能力，能够克服KSW算法抗干扰能力弱的缺点，提高图像的分割精度，并求解到更优的阈值.

(3)从时间上分析，KSW算法运行效率较高，但由于其鲁棒性差，分割精度低，在实际应用中并不占优势.PSO算法时间复杂度与迭代次数和维数线性相关，因此时间复杂度相对较高，运行时间慢，效率低，是PIO算法运行所用时间的两倍，且通过对算法的分析，得出其在解决多峰值问题时易陷入局部最优解，因此出现停滞现象而搜索不到更好的解.

(4)PIO算法不仅可以更加清晰地分割出前景与背景，而且对于单峰和多峰图像分割效果均理想，具有较强的鲁棒性和精确性，同时，采用地标算子和地磁场相结合的方式进行寻解，避免了算法陷入局部最优解，更优的寻解能力也使得该算法的收敛速度明显更有优势，运算效率有效提高，在实际应用中可以满足图像的实时性要求.

3.3 参数灵敏度分析

为了进一步优化PIO算法，对同一张图片在不同PIO算法种群数参数下进行处理，分析参数对算法结果的影响.图8～9给出了时间以及重叠率与种群数关系的拟合结果.

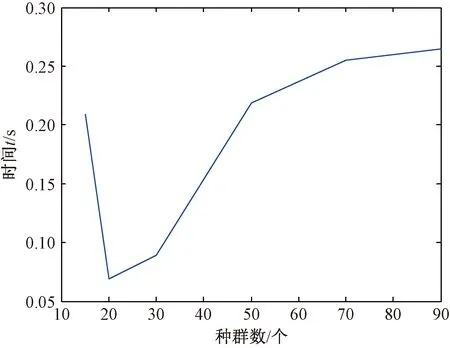
图8 算法时间随种群数的变化Fig.8 Algorithm time varies with population

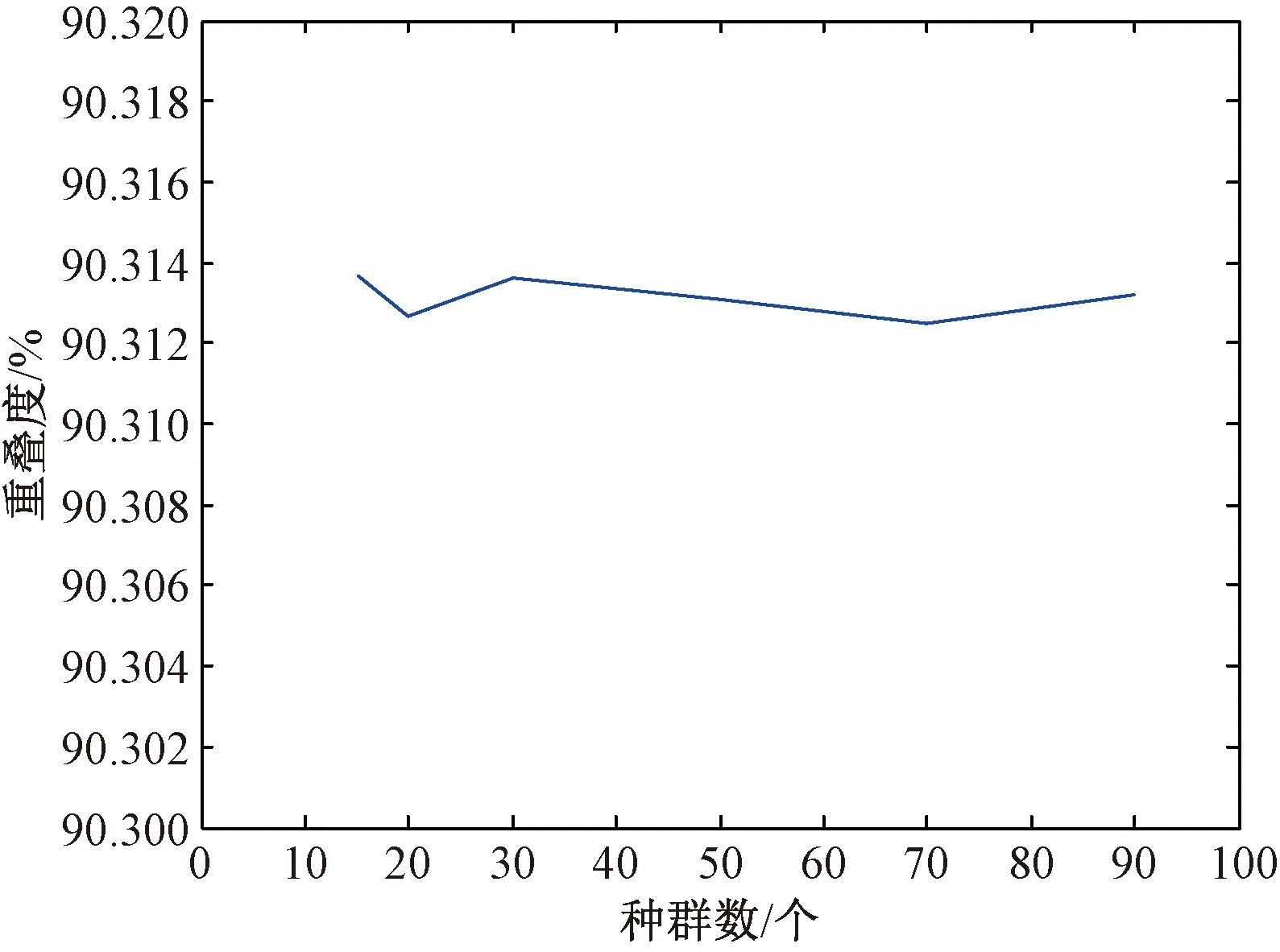
图9 重叠度随种群数的变化Fig.9 The degree of overlap varies with population size

从图8和图9可以看出，运算时间随着种群数量的增加呈显著增加趋势，而重叠度相对于种群数量变化较小.因此PIO算法解决图像分割问题仅依赖少量种群，即仅需少量时间就可以得到较好的分割结果.具体而言，当种群数为30时，PIO算法分割图像的结果最好，并且算法时间也比较小.

4 结论

笔者针对传统图像阈值分割方法最优阈值选择不理想且分割效率低等问题，提出了一种基于PIO优化算法的图像分割方法.该方法以分割阈值为优化变量，图像范围为约束条件，建立有约束优化方程，然后以随机的分割阈值作为迭代初值，采用PIO算法求解得到最优阈值，最后采用最佳阈值进行图像分割.PIO仿真以及与PSO、KSW算法对比结果表明，本文算法在时间和重叠度上均具有优势，具有很好的鲁棒性与适应性，且运算效率高,收敛速度快，具有更强的寻优能力，因此对于图像分割具有精确性和高效性的优点.