广府古建筑木结构箍头榫节点弯矩-转角关系理论分析
2019-07-19陈庆军何永鹏邱凯祥汤序霖蔡健杨春
陈庆军 何永鹏 邱凯祥 汤序霖 蔡健 杨春

摘 要:广府祠堂木结构节点多采用箍头榫形式,其受力性能与已有的直榫、燕尾榫等均存在差異,为研究箍头榫节点的受力性能,开展了箍头榫节点的受力机理分析,推导了弯矩-转角理论计算公式,并通过试验结果验证了理论计算公式的正确性;基于理论计算公式,对影响箍头榫节点弯矩-转角关系的各个因素进行分析.分析结果表明,在所计算的参数范围内,节点初始转动刚度和极限弯矩随着柱直径、榫宽度、摩擦系数、榫头侧面和卯口间挤压宽度的增大而增大,节点极限弯矩随着梁高增大而增大,而节点初始转动刚度受梁高的影响不大.所得结果可为广府地区古建筑木结构的受力分析及抗震性能研究提供理论依据.
关键词:古建筑;木结构;箍头榫节点;受力机理;弯矩-转角关系
中图分类号:TU366 文献标志码:A
文章编号:1674—2974(2019)01—0065—11
Abstract:Hoop head tenon-mortise joint is extensively adopted in an ancient timber structure in Guangfu, which is different from straight tenon-mortise joint or dovetail tenon-mortise joint in terms of mechanical performance. To analyze the mechanical properties of hoop head tenon-mortise joint,mechanism analysis was carried out and the moment-rotation calculation formulae were also derived, while the formulae were verified by experimental results. Using the formulae,the factors affecting the relationship of moment-rotation of hoop head tenon-mortise joint were investigated. The results indicate that within the range of parameters, the initial rotational stiffness and ultimate bending moment increase with the increase of the column diameter, mortise width, friction coefficient and unilateral compression width between tenon and mortise,while the ultimate bending moment increases with the increase of beam height, but the initial rotational stiffness is only slightly affected by the beam height. The results of this study can serve as a theoretical foundation for mechanical analysis as well as for seismic research of ancient timber structures in Guangfu.
Key words:ancient architecture;timber structures;hoop head tenon-mortise joint;force mechanism;moment-rotation relationship
中国古建筑木结构具有丰富的历史文化内涵和极高的科学价值,如何对它们进行有效的评估和保护一直是研究者们研究的热点.古建筑木结构中各构件之间常采用榫卯进行连接.榫卯节点通过交界面的挤压和摩擦来抵抗外力与耗散能量,其受力机理较为复杂.谢启芳等[1]、周乾等[2]对汶川地区古建筑的震害调研发现,古木建筑的破坏特征主要表现为榫卯节点拔榫或松动.开展对古木结构榫卯节点力学性能的研究并提出合适的修缮保护方法具有重要意义.
由于木结构榫卯节点呈现出典型的半刚性,且节点的转动刚度随着节点转角变化而变化,因而节点弯矩-转角关系是木结构研究中的一个重点问题.淳庆等[3]通过低周反复荷载试验和有限元模拟分析,研究了江南地区传统木构建筑半榫节点的受力性能.部分学者在试验研究基础上,根据节点弯矩-转角曲线的特点提出了相应的力学计算模型,以便应用于整体模型计算中.高大峰等[4]在榫卯节点试验的基础上建立了燕尾榫节点的弯矩-转角及荷载-位移四阶段恢复力模型.赵鸿铁等[5]根据试验中得到的燕尾榫节点弯矩-转角骨架曲线,拟合得到了节点的弯矩-转角的关系方程和恢复力模型.Kishi等[6]在试验基础上提出了节点弯矩-转角的3参数幂函数模型,结果表明该模型可以较好地反映节点的刚度特性.杨艳华等[7]在试验研究基础上,对原有3参数幂函数弯矩-转角模型进行改进,建立了适用于木结构榫卯节点的4参数幂函数模型.淳庆等[8]以中国南方典型榫卯节点为研究对象,将试验得到的典型节点的弯矩-转角骨架曲线简化为三折线模型并算出了模型各阶段的特征刚度.
以上研究中,榫卯节点弯矩-转角关系中的关键参数大多根据试验结果简化或拟合得到.部分學者对若干形式的榫卯节点进行了更为深入的受力机理分析,推导得到节点的弯矩-转角理论计算公式,提出了相应的力学计算模型.姚侃等[9]引入了变刚度杆单元来描述榫卯连接的半刚性特性,推导出了榫卯节点的变刚度与相对柔度之间的关系.徐明刚[10]在燕尾榫节点和木框架试验的基础上,考虑了节点缝隙、残余变形和轴力的影响,对榫卯节点进行受力机理分析并建立了节点的转角-弯矩理论计算模型.谢启芳等[11-12]分析了燕尾榫节点的受力机理,推导了节点的弯矩-转角理论计算公式并分析了各节点参数对节点弯矩-转角关系的影响,提出了以屈服点和极限点为特征点的弯矩-转角双折线力学模型.谢启芳等[13]以单向直榫节点为研究对象,分析其受力机理,推导了节点转动弯矩-转角理论计算公式,对影响单向直榫节点转动弯矩的参数进行了分析.潘毅等[14]分析直榫节点在低周反复荷载作用下的受力机理,推导并建立了直榫节点的弯矩-转角力学模型,对力学模型进行简化并提出了直榫节点的三折线力学计算模型.陈春超等[15-16]在试验研究和数值分析的基础上,对瓜柱直榫和燕尾榫节点进行了受力机理分析,推导了典型节点的弯矩-转角理论计算公式,并提出了简化力学模型.
广府祠堂木结构是一种介于高级殿堂及普通民宅之间的建筑体系,该类建筑大多建于明清时代,是以广州为中心的泛珠三角地区古木建筑的重要代表.广府木祠堂中常采用箍头榫节点进行连接,其构造形式具有明显的地域特征.由于修建年代久远且遭受广东地区潮热气候的侵蚀,现存的广府木祠堂建筑存在不同程度的残损,迫切需要对其加以保护和修缮.而目前针对广府木祠堂建筑箍头榫节点进行的研究较少[17-18],这制约了广府祠堂木结构的修缮保护工作.因此,为进一步研究典型箍头榫节点的工作机理,本文对箍头榫节点进行受力分析,根据节点的几何条件、平衡条件以及物理条件,推导出典型节点的弯矩-转角理论计算公式,将理论分析的计算结果与试验数据进行对比从而验证了计算结果的准确性;基于理论计算公式,研究梁截面高度、柱直径、榫宽度、榫头和卯口之间的侧面挤压宽度、摩擦系数对节点弯矩-转角关系的影响.
1 箍头榫节点受力机理
箍头榫是广府地区古木建筑中常用的连接形式之一.如图1所示,柱头上部横向开口形成卯口,梁在相应位置削减截面使其恰好能放进柱卯口.节点安装时,先使柱就位,再将梁移动到柱顶位置,对准梁榫头与柱卯口的位置,将梁摆放到柱卯口中,使位于柱内外侧的梁榫头与柱卯口互相咬合,然后将垫块放入柱顶开口处,将栓销插进垫块与柱顶圆孔,完成节点安装.相比直榫连接,由于柱内外侧梁榫头与柱卯口相互咬合,节点能够较好抵抗受压及拉拔作用.节点发生转角时,梁榫头与柱卯口同时受挤压,产生抵抗弯矩.箍头榫节点相比直榫节点而言,抗拔性能更好、整体性更强,但制作及施工相对复杂.箍头榫的榫卯尺寸参见图2.
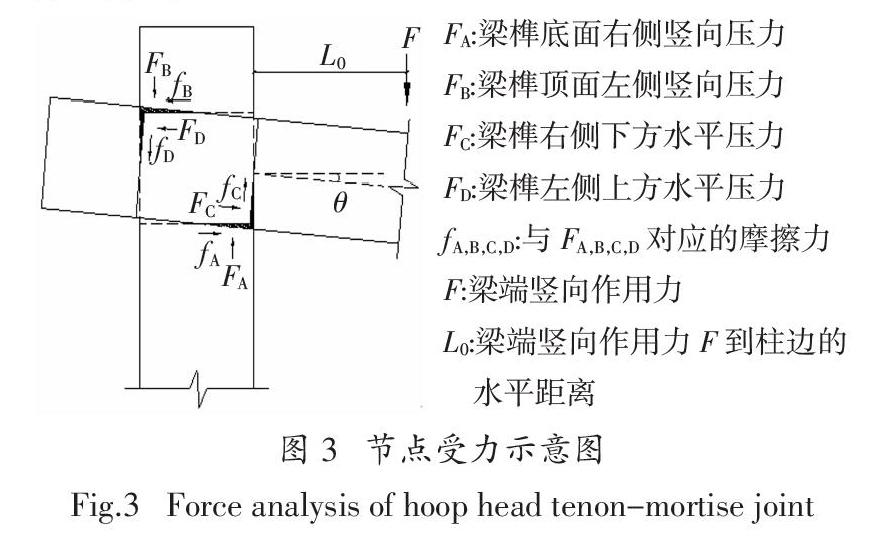
如图3所示,当节点梁柱之间产生正向相对转角θ时,榫卯之间相互挤压并产生变形,此时梁榫顶面左侧和底面右侧受到柱子作用的竖向压力和相应的水平摩擦力,同时梁榫左侧上方和右侧下方也受到柱子的水平压力和相应的摩擦力,这些挤压力和摩擦力的作用使节点产生了抵抗转动的弯矩.随着节点转角增大,榫卯之间挤压处逐渐产生塑性变形,榫头和卯口之间发生脱离,但由于箍头榫节点的特殊榫卯构造,柱卯口可以较好地约束榫头向外拔出,因而相比直榫、燕尾榫等,箍头榫节点的拔榫量始终较小.
2 箍头榫节点弯矩-转角关系理论分析
2.1 基本假定
1)由于木材顺纹方向受压弹性模量远大于横纹受压弹性模量,当榫卯之间发生挤压时,一方为横纹受压而另一方为顺纹受压,则本文假设只有横纹受压一方会产生挤压变形[19].
2)假定木材横纹受压的本构为双线性强化本构模型,且其应力-应变关系符合胡克定律[20-21].
3)根据文献[21]试验结果可知,榫头与卯口两侧面之间的摩擦力较小,为方便计算,假定榫头与卯口两侧面的摩擦力为零.
4)假定榫头在卯口内仅发生刚体运动[16],因而忽略节点榫头和卯口的弯曲变形.
2.2 箍头榫节点弯矩-转角关系理论公式推导
为简化计算,将箍头榫节点的受力过程近似分为两个阶段来进行分析:1)榫头和卯口挤压面处的变形均处于弹性阶段;2)榫头和卯口挤压面处的变形均进入弹塑性阶段.
2.2.1 弹性阶段
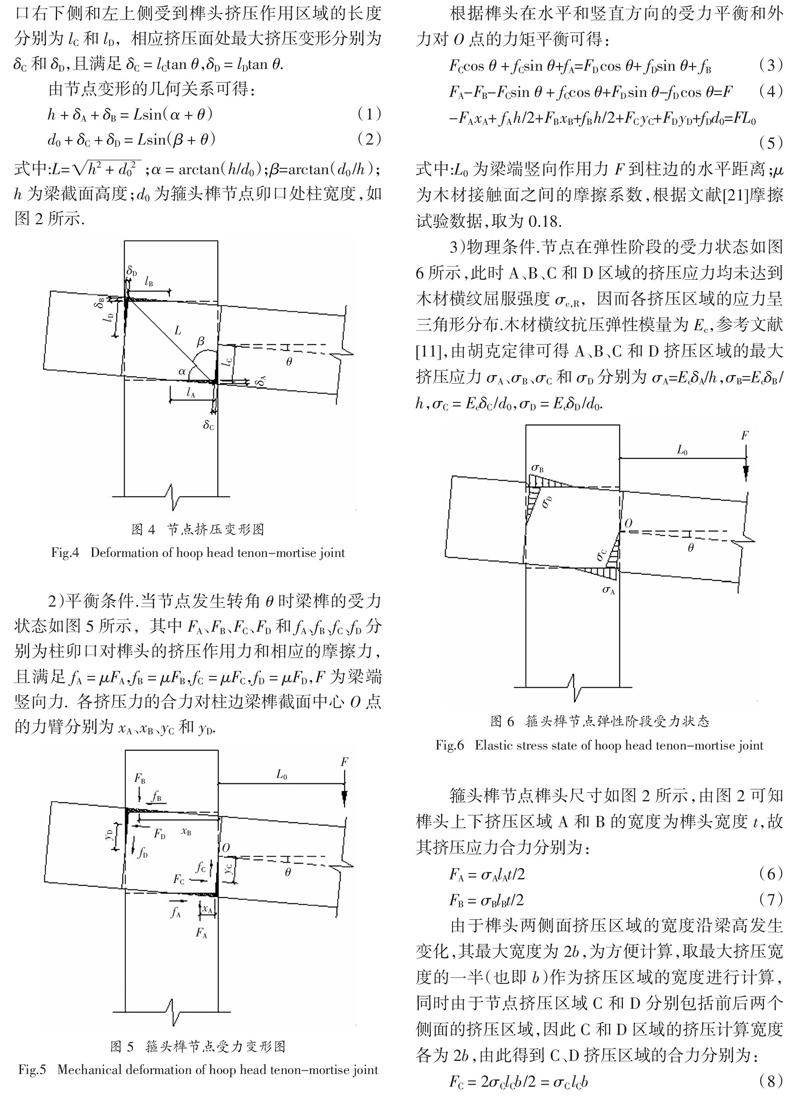
1)几何条件.当节点发生正向转角θ时,节点挤压变形如图4所示.定义榫头底面和顶面挤压区域的长度分别为lA和lB,相应挤压面处最大挤压变形分别为δA和δB,且满足δA = lAtan θ,δB = lBtan θ;柱卯口右下侧和左上侧受到榫头挤压作用区域的长度分别为lC和lD,相应挤压面处最大挤压变形分别为δC和δD,且满足δC = lCtan θ,δD = lDtan θ.
由节点变形的几何关系可得:
2)平衡条件.当节点发生转角θ时梁榫的受力状态如图5所示,其中FA、FB、FC、FD和fA、fB、fC、fD分别为柱卯口对榫头的挤压作用力和相应的摩擦力,且满足fA = μFA,fB = μFB,fC = μFC,fD = μFD,F为梁端竖向力.各挤压力的合力对柱边梁榫截面中心O点的力臂分别为xA、xB、yC和yD.
根据榫头在水平和竖直方向的受力平衡和外力对O点的力矩平衡可得:
式中:L0为梁端竖向作用力F到柱边的水平距离;μ为木材接触面之间的摩擦系数,根据文献[21]摩擦试验数据,取为0.18.
3)物理条件.节点在弹性阶段的受力状态如图6所示,此时A、B、C和D区域的挤压应力均未达到木材横纹屈服强度σc,R,因而各挤压区域的应力呈三角形分布.木材横纹抗压弹性模量为Ec,参考文献[11],由胡克定律可得A、B、C和D挤压区域的最大挤压应力σA、σB、σC和σD分别为σA=EcδA/h,σB=EcδB /h,σC = EcδC /d0,σD = EcδD /d0.
箍头榫节点榫头尺寸如图2所示,由图2可知榫头上下挤压区域A和B的宽度为榫头宽度t,故其挤压应力合力分别为:
由于榫头两侧面挤压区域的宽度沿梁高发生变化,其最大宽度为2b,为方便计算,取最大挤压宽度的一半(也即b)作为挤压区域的宽度进行计算,同时由于节点挤压区域C和D分别包括前后两个侧面的挤压区域,因此C和D区域的挤压计算宽度各为2b,由此得到C、D挤压区域的合力分别为:
由于各挤压区域的应力呈三角形分布,因此可得到A、B、C和D挤压区域的合力对O点的力臂为xA = lA/3,xB = d0 - lB/3,yC = h/2 - lC/3,yD = h/2 - lD/3.
以lB、lD为基本变量,结合δA=lAtan θ,δB=lBtan θ,δC = lCtan θ,δD = lDtan θ及式(1)(2),用lB、lD表示lA、lC;lA、lC用lB、lD表示后,σA,B,C,D也可以通过lB、lD表示,进而可以用lB、lD表示FA(B,C,D)、fA(B,C,D).将FA(B,C,D)、fA(B,C,D)代入平衡方程(3)~(5)中并消去物理量F,可化简得到两个关于lB、lD的二元三次方程F1(lB、lD)=0,F2(lB、lD)=0,联立求解此方程组可得到lB、lD,进而计算得到FA~FD、fA~fD等8个未知数.则节点弯矩Me可表示为:
弹性阶段时,对于任意转角值θ,节点弯矩Me的求解过程见图7.
2.2.2 弹塑性阶段
与弹性阶段相似,节点弹塑性阶段的几何方程和平衡方程如式(1)~(5)所示.节点在弹塑性阶段的受力状态如图8所示,此时A、B、C和D挤压区域的最大应力均已达到或超过木材的横纹初始屈服强度σc,R,因而各挤压区域的应力呈四边形分布.
各挤压区域的最大擠压应力分别为:
式中:E2为木材横纹受压强化阶段的切线模量,根据文献[21]材料性能试验数据,取E2 = 0.30Ec.
各挤压区域的应力呈四边形分布,定义各挤压区域已经屈服的挤压长度分别为lA1、lB1、lC1和lD1,且有lA1 = lA - σc,Rhtan θ/Ec,lB1 = lB - σc,Rhtan θ/Ec,lC1 = lC - σc,Rd0 tan θ/Ec,lD1 = lD - σc,Rd0 tan θ/Ec.由此可得A、B、C和D挤压区域的合力:
以挤压区域A为例,其应力呈四边形分布,通过求解其形心可得到挤压区域A的合力对O点的力臂如式(19)所示,同理可求得B、C和D挤压区域的合力对O点的力臂xB、yC、yD.
弹塑性阶段时任意转角下节点弯矩Mp的求解过程与弹性阶段的弯矩Me类似,可参考图7进行,Mp可表示为:
对处于区间[0,θmax](θmax为极限转角)的θ,可按以上公式求解得到节点处于弹性阶段的弯矩Me和处于塑性阶段的弯矩Mp,当Me = Mp时,对应的θ为节点由弹性阶段向弹塑性阶段转变时的界限转角,Me(Mp)为界限弯矩.当节点转角小于界限转角时节点弯矩值为Me,当节点转角大于界限转角时节点弯矩为Mp,由此可以得到节点在整个加载过程中的弯矩-转角关系.反向加载时节点弯矩-转角理论计算公式的推导过程与正向加载类似,此处不再赘述.
文献[21]的试验结果表明,箍头榫节点试件在临近破坏时榫头顶面或底面出现了不同程度的顺纹受拉断裂现象,因此定义极限转角之一θmax,1为榫头顶面木材达到顺纹极限拉应变时的节点转角.文献[21]给出了对应极限转角θmax,1的榫头截面弯矩Mmax,1的表达式:
根据Mmax,1,结合式(20),可反推得到极限转角θmax,1.
此外,根据文献[21]的试验结果,可知对于加载过程中未出现榫头顶面或底面受拉断裂的试件,此类节点破坏时的极限转角约为0.15 rad.因此,极限转角θmax取min{θmax,1,0.15 rad}.
3 节点弯矩-转角理论计算结果验证
为了验证箍头榫节点弯矩-转角理论计算公式的合理性,将本文的理论计算结果与文献[21]的试验结果进行对比分析.
文献[21]以梁高h、柱直径D、榫宽t和柱顶轴压力P为试验参数,以1 ∶ 2.7的缩尺比例设计制作了8个单向箍头榫节点试件进行低周反复荷载试验.箍头榫节点尺寸构造见图9(a),试件编号为S1~ S8,各试件的基本设计参数见表1.试验所用木材为菠萝格,其物理力学性能如表2所示.试验加载装置如图9(b)(c)所示.
文献[21]试验结果表明,在所研究的参数范围内,柱顶轴压力P对节点力学性能影响不大,而改变梁高h、柱直径D、榫宽t会对节点的弯矩-转角关系产生较大影响.
由式(10)和式(20)计算得到的各节点弯矩-转角理论计算曲线与文献[21]试验骨架曲线的对比图绘制于图10,由图10可以看出:
1)节点的转角较小时,各节点理论计算曲线与试验曲线的变化趋势基本相同,节点弯矩近似随着转角的增大而线性增大,因而理论计算公式可以较好地反映节点弹性阶段的力学性能;随着节点转角增大,木材出现塑性变形,理论与试验曲线的趋势大体相同且曲线的斜率均有一定程度的下降,表明理论计算公式可以较好地反映节点塑性阶段的力学性能.总体而言,节点理论计算曲线与试验曲线的变化趋势、节点初始刚度和极限弯矩均吻合较好,表明理论计算公式可以较好地反映箍头榫节点的力学特征.但由于试验结果受到材料缺陷和加工误差等无法精确计算的因素的影响,因而计算结果中个别模型的节点刚度和承载力与试验结果存在一定程度的差异.
2)对于试件S2、S4和S5,节点反向加载初期的刚度计算值大于试验值,这是因为试件制作加工时梁上部榫卯之间存在一定空隙,因而其反向加载初期节点刚度较小,直到榫卯之间接触紧密后节点刚度才逐渐增大,而理论计算公式中没有考虑榫卯之间的空隙,因而其初始刚度较大.
3)由于理论计算方法中未考虑节点正反向加载时受力状态的差异,因而节点正反向加载时的弯矩-转角曲线是关于原点对称的,这与试验结果有一定的差异.
4 弯矩-转角理论关系影响因素分析
由理论分析得到的弯矩-转角理论计算公式(式(10)、式(20))并结合文献[21]的试验结果可知,影响箍头榫节点弯矩-转角关系的参数包括梁高度h、柱直径D、榫宽度t、摩擦系数μ和榫头侧面和卯口挤压区域宽度b.基于文献[21]的试件尺寸参数,分别对各影响因素展开理论分析.以下“试件S1”均指文献[21]中的试件S1.
4.1 梁高h的影响
以试件S1的参数为原型,在其余各影响因素保持不变的情况下,分别取梁高度为110 mm、130 mm、150 mm和170 mm,计算得到不同梁高下箍头榫节点的弯矩-转角曲线如图11所示.转角为0.12 rad时,梁高从110 mm变化到170 mm,梁高增大55%,节点弯矩约增大13%,相当于梁截面高度每增加1%,节点弯矩提高0.24%.当梁高为110~170 mm时,箍头榫节点的极限弯矩随着梁高的增大而增大.此外,计算结果表明梁高大小对节点的初始转动刚度影响很小.
4.2 柱直径D的影响
以试件S1的参数为原型,在其余各影响因素保持不变的情况下,分别取柱直径为110 mm、130 mm、150 mm、170 mm和190 mm,计算得到不同直径下箍头榫节点的弯矩-转角曲线如图12所示.当转角为0.12 rad时,柱直径从110 mm变化到190 mm,柱直径增大73%,节点弯矩约增大186%,相当于柱直径每增加1%,节点弯矩提高2.55%.由图12可看出,当柱直径为110~190 mm时,箍头榫节点的初始刚度和极限弯矩随著柱直径的增大而增大.
4.3 侧面挤压宽度b的影响
以试件S1的参数为原型,在其余各影响因素保持不变的情况下,分别取侧面榫头和卯口挤压宽度b为5.25 mm、10.50 mm、15.75 mm、和21.00 mm,计算得到不同挤压宽度下箍头榫节点的弯矩-转角曲线如图13所示.当转角为0.12 rad时,侧面挤压宽度从5.25 mm变化到21.00 mm,侧面挤压宽度增大3倍,节点弯矩约增大38%,相当于侧面挤压宽度每增加1%,节点弯矩提高0.13%.由图13可看出,当侧面榫卯挤压宽度为5.25 ~ 21.00 mm时,箍头榫节点的初始刚度和极限弯矩随着侧面榫卯挤压宽度的增大而增大.
4.4 榫宽度t的影响
以试件S1的参数为原型,在其余各影响因素保持不变的情况下,分别取榫宽度为0.2D(30 mm)、0.3D(45 mm)、0.4D(60 mm)和0.5D(75 mm),计算得到不同榫宽度下箍头榫节点的弯矩-转角曲线如图14所示.
由图14可看出,当转角为0.12 rad时,榫宽从0.2D变化到0.5D,榫宽增大1.5倍,节点弯矩大约增大93%,相当于榫宽每增加1%,节点弯矩提高0.62%.当榫宽由0.2D增大到0.5D时,箍头榫节点的初始刚度和极限弯矩随着榫宽度的增大基本呈增大的趋势.理论推导过程中假设榫头和卯口均没有弯曲变形,当榫宽度大于0.5D时,两侧柱卯口的厚度较小,卯口抗弯刚度较小,柱卯口区域会产生一定的弯曲变形,故而通过式(10)和式(20)计算得到的节点初始刚度和极限弯矩比实际值偏大.因此认为当榫宽大于0.5D时,本文弯矩-转角理论公式的计算精度将下降.
4.5 木材间摩擦系数μ的影响
文献[22-24]的研究结果表明,不同种类和粗糙度木材之间的摩擦系数取值约为0.10~0.65,因此本文以试件S1的参数为原型,在其余各影响因素保持不变的情况下,分别取木材之间的摩擦系数μ为0.10、0.18、0.30、0.40、0.50和0.60,计算得到不同摩擦系数下箍头榫节点的弯矩-转角曲线如图15所示.当转角为0.12 rad时,摩擦系数从0.10变化到0.60,摩擦系数增大5倍,节点弯矩大约增大67%,相当于摩擦系数每增加1%,节点弯矩提高0.13%.当摩擦系数由0.1增大到0.6时,箍头榫节点的初始刚度和极限弯矩均随摩擦系数的增大而增大.
5 结 论
本文基于典型箍头榫节点的受力机理分析,对节点弯矩-转角理论关系进行了推导并通过试验结果验证了理论计算公式的正确性;通过对影响箍头榫节点弯矩-转角关系的各个因素进行分析,得到了各因素对节点初始刚度和极限弯矩的影响规律.得到以下结论:
1)推导了典型箍头榫节点弹性阶段和弹塑性
阶段的弯矩-转角理论关系,并得出了相应的理论计算公式;对比理论计算结果与试验结果可知,理论计算与试验得到的节点弯矩-转角曲线在弹性阶段与弹塑性阶段均吻合较好,表明理论计算公式可以较好地反映出节点的力学特征.
2)对影响箍头榫节点弯矩-转角关系的因素分析后发现,在所计算的参数范围内,箍头榫节点的初始刚度和极限弯矩随着柱直径、榫宽度、摩擦系数、榫头侧面和卯口挤压区域宽度的增大而增大.随着梁高增大,节点极限弯矩逐渐增大,但节点初始刚度变化不大.同时发现,柱直径的变化对接近极限状态的节点弯矩的影响最大,榫宽次之,梁高再次之,侧面挤压宽度和摩擦系数的影响最弱.
