不同地震动情况下的大跨度连续刚构桥梁响应分析

黄 辉

(西南交通大学土木工程学院, 四川成都610031)

我国处于地震频发地区，地震发生频率高，地震震级大，对于桥梁结构产生的破坏是巨大的。对于处于交通咽喉位置的桥梁结构，如果设计未能充分考虑地震作用带来的危害，可能发生地震作用下桥梁垮塌等事故，从而破坏交通线路影响抗震救灾工作[1-2]。因此，对于桥梁结构进行抗震分析计算具有重要的意义。本文以一座大跨度连续刚构桥为研究对象，采用有限元方法，建立用于动力分析的杆系模型，对结构的地震响应进行详细的计算和分析，为类似桥型的抗震设计提供参考。

1 工程概况

犍为岷江二桥是一座特大型桥梁，桥梁全长2 029m。主桥为预应力混凝土连续刚构桥，桥跨布置为118m+ 215m+ 118m，主梁采用单箱单室截面，全宽13m，箱梁高度由桥墩处13.75m按照1.6次曲线变化至跨中处及端部4.6m。同时，箱梁顶底板及腹板厚度均由支座处向跨中处递减，顶板厚度在0.3～0.5m变化，底板厚度在0.32～1.46m变化，腹板厚度在0.5～0.7m变化。主墩墩身高度约30.0m，采用钢筋混凝土双肢薄壁墩身，承台接钻孔灌注桩基础；每个墩身双肢间净距6.0m，每肢纵向厚度2.0m，横向宽度8.5m，两侧为圆端型；承台采用整体式，顺桥向长16.0m，横桥向宽30.0m，厚5.5m；基础按嵌岩桩设计，一个承台采用18根直径2.5m钻孔灌注桩。主桥总体布置如图1所示。

图1 主桥总体布置(单位:m)

2 计算模型

采用大型有限元软件MidasCivil建立岷江二桥的动力计算模型。计算模型中主梁、薄壁墩采用梁单元模拟，主梁线形根据每个截面的形心轴确定，全桥共划分单元196个。模型边界条件为: 主墩底完全固结，边跨端部采用弹性连接刚接，约束竖向、横向和绕桥纵轴向的位移，主墩和主梁连接部位采用刚性连接。模型参数取值为：主梁混凝土强度等级C60，弹性模量3.6×104MPa，泊松比0.2，容重25kN/m3；主墩混凝土强度等级C50，弹性模量3.45×104MPa，泊松比0.2，容重25kN/m3，重力加速度g=9.81m/s2.主桥动力计算模型如图2所示。

图2 主桥有限元模型

3 结果分析

根据动力计算模型，采用多重Ritz向量法计算得到大跨度连续刚构桥的动力特性，共计算了主桥前50阶振型，前10阶振型的周期、频率和振型特征如表1所示，图3给出了前10阶的振型图。从表1和图3可以看出：岷江二桥的结构基频为0.729 0Hz，小于一般连续刚构体系的基频，这表明双肢薄壁墩能够在一定程度上使得桥梁整体结构具有柔性特征；前10阶振型中有5阶为纵向偏移，其中第2阶纵桥向质量参与系数为21.16 %，由于桥墩高度较大，有可能在顺桥向产生较大塑形转角，应加强塑性铰区域的设计和处理。

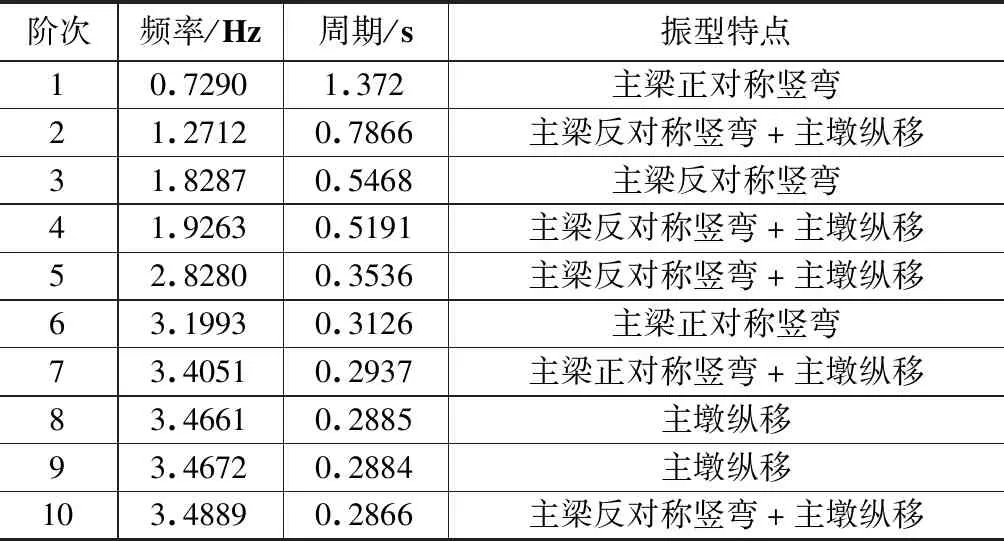
表1 模型前10阶振型动力特性及振型特点

第1阶振型

第2阶振型

第3阶振型

第4阶振型

第5阶振型

第6阶振型

第7阶振型

第8阶振型

第9阶振型

第10阶振型图3 模型前10阶振型示意

本文采用时程法(线性)分析连续刚构桥的地震响应。岷江二桥桥址处地震基本烈度7级，50年超越概率10 %地震动加速度为0.095g，场地类别为II类中软场地类型，因此须按8度设防，采用EI-Centro波作为地震动输入。同时，对EI-Centro波进行修正，使得水平方向的地震波加速度峰值为0.3g，对于其周期则不予修正。输入的EI-Centro地震波加速度时程曲线如图4所示。

图4 地震波加速度时程曲线

在一致激励情况下，考虑地震运动方向的多维特性，输入的地震波激励为：纵桥向+竖向，纵桥向为水平地震波，竖向为竖向地震波，竖向波峰值为水平波的2/3。图5给出了时程法求解的控制截面响应——24#主墩左肢和25#主墩右肢底部顺桥向弯矩响应。

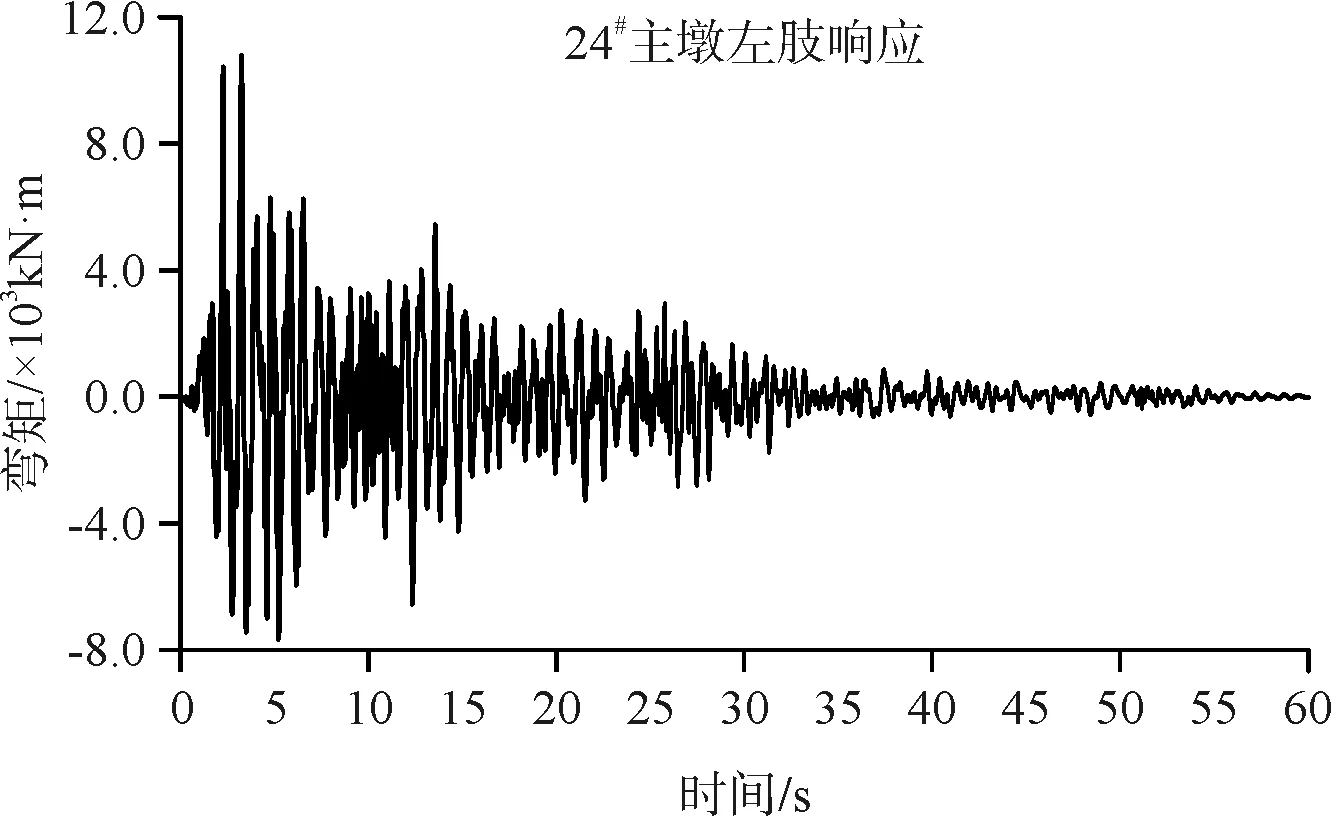
(a)X方向地震动24#主墩左肢响应

(b)X方向地震动25#主墩左肢响应

(c)Z方向地震动24#主墩左肢响应

(d)Z方向地震动25#主墩左肢响应

(e)X-Z方向地震动24#主墩左肢响应

(f)X-Z方向地震动25#主墩左肢响应图5 地震波加速度时程曲线

从图5中可以看出，在X方向地震动单独作用时，24#主墩左肢的最大弯矩响应峰值为1.080×104kN·m，发生在3.230s；25#主墩右肢的最大弯矩响应峰值为1.080×104kN·m，发生在3.230s。在Z方向地震动单独作用时，24#主墩左肢的最大弯矩响应峰值为8.086×103kN·m，发生在5.480s；25#主墩右肢的最大弯矩响应峰值为8.067×103kN·m，发生在5.480s。而当考虑多维地震动时，24#主墩左肢的最大弯矩响应峰值为1.108×104kN·m，发生在2.490s；25#主墩右肢的最大弯矩响应峰值为1.740×104kN·m，发生在2.240s。可以看出，多维地震动情况下，桥梁结构的各阶振型被直接或间接的激发，表现出空间耦合特征。对于不同的地震动情况，桥梁关键截面响应峰值和对应时间均不同。因此，在多维地震激励时，应考虑到与一维地震激励情况下结构内力和位移的不同，合理设计结构。

4 结论

本文以一座连续刚构桥为工程背景，通过建立其有限元模型，对岷江二桥的动力特性进行了计算，并采用时程法(线性)对其地震响应进行了分析，得出如下结论。

(1)岷江二桥的结构基频为0.729 0Hz，小于一般连续刚构体系的基频，这表明双肢薄壁墩能够在一定程度上使得桥梁整体结构具有柔性特征；前10阶振型中有5阶为纵向偏移，由于桥墩高度较大，有可能在顺桥向产生较大塑形转角，应加强塑性铰区域的设计和处理。

(2)在多维地震动作用下，桥梁结构内力响应具有一定的空间耦合性。因此，在抗震分析和设计时，只采用一维地震激励输出得到的结果偏于不安全，应当采用与实际相近的多维地震激励。