基于分位数回归方法的函数型数据在线控制图

2019-07-19张秀玲訾雪旻

天津职业技术师范大学学报 2019年2期

张秀玲，訾雪旻

（天津职业技术师范大学理学院，天津 300222）

利用函数型数据刻画产品的某些特性，进而分析和监控此类函数型数据是统计过程控制领域研究的热点问题之一。目前，很多研究都是基于传统最小二乘估计的方法监控模型的回归系数，从而建立有效控制图。然而，相对于仅关注响应变量在解释变量已知情况下条件期望的变化，在实际应用中监控响应变量条件中位数或其他条件分位数的变化越来越受到学术界的重视。如2001年，Abrevaya[1]分析影响低体重新生儿因素问题；2001年，Bassett等[2]评估共同基金的投资类型；2005—2006年，Machado等[3-4]研究劳动力市场、工资结构分布等。假定样本均值是位置参数的最优估计的关键取决于假设观测值来自一般的正态分布。如果观测值不是来自同一个分布，如来自不同方差的正态分布，采用中位数做估计明显比用均值做估计效果更好。自1978年Koenker等[5]提出的分位数回归以来，出现了很多关于分位数回归的研究，然而对于构造其应用统计过程控制中相应的控制图这一问题研究相对较少。本文针对上述问题，基于分位数回归方法结合多元指数加权移动平均控制图（MEWMA），给出一种新的函数型数据在线监控控制图，并通过数值模拟说明该控制图的有效性。

1 监控线性函数型数据的MEWMA控制图

对一般线性函数型模型和2007年Zou等[6]基于最小二乘估计方法建立的MEWMA控制图进行描述。假设随着时间收集第j个时刻的随机样本，则有观测值（Xj，Yj），其Yj=（y1j，y2j，…，ynjj）′是nj维响应变量，Xj是nj×p（nj＞p）矩阵。当统计过程可控时，假设基本模型为：

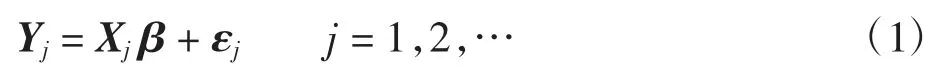
式中：β=（β1，β2，…，βp）′是p维系数向量；误差项εj=（ε1j，ε2j，…，εnjj）′都是独立同分布于均值为0且协方差阵为σ2I的nj维多元正态随机向量。

在不失一般性的前提下，假设Xj的形式是（1，Xj*），其Xj*是正交于1，1是nj维常数向量且所有分量都是1。否则也可以通过合适的变换得到这种形式。通常nj都是相等的（记作n），假设对不同时刻j的解释变量Xj是固定的（记作X）。

将随着时间收集的第j个时刻的随机样本记作{（xi，yij），i=1，2，…，n}。当统计过程可控时，假设响应变量和解释变量的关系为：

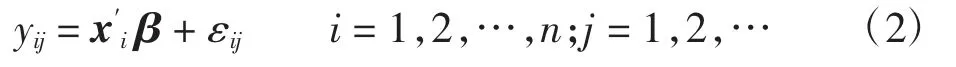
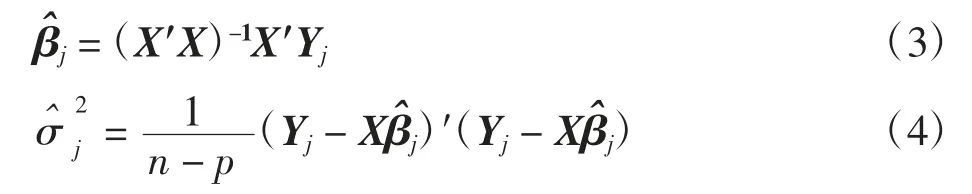
Zou等[6]用MEWMA控制图同时监控模型（2）的截距β0、斜率β1和标准差σ。根据模型（1）定义：

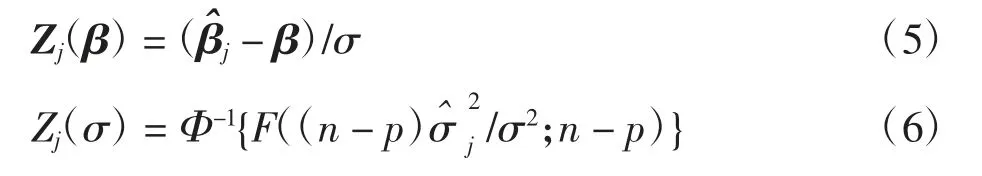
式中：Φ-1（·）为标准正态累积分布函数的反函数；F（·；v）为自由度v的卡方分布函数即（σ））′是（p+1）维随机向量。当统计过程可控时，Zj服从均值为0且协方差阵为∑的多元正态分布，其∑=将EWMA控制图统计量定义为：

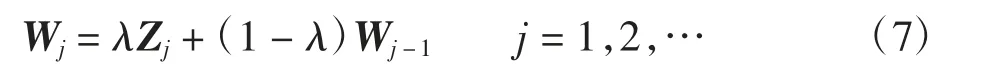
式中：W0为（p+1）维初始向量；λ为光滑参数且0＜λ≤1。若：

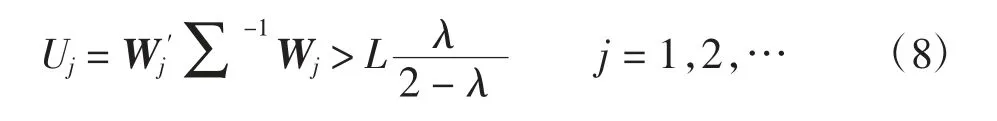
控制图就会报警。

式中：L为控制限且L＞0。

Zou等[6]通过比较失控平均运行长度说明MEWMA控制图比Kim等[7]3 个EWMA结合的控制图能更有效地探测截距、斜率和标准差发生的漂移。

2 分位数回归方法

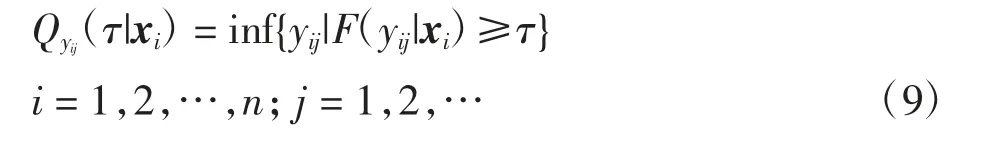
式中：τ为下分位数且τ∈（0，1）。

式（9）是xi的线性函数，即：

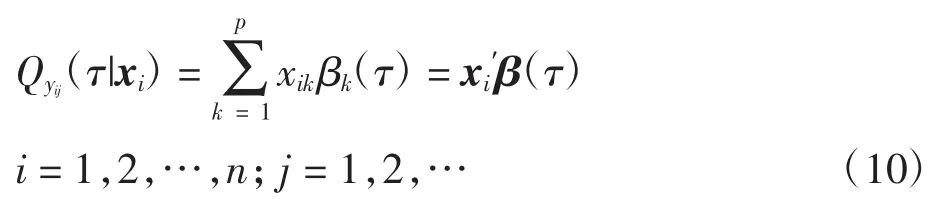
式中：xi′=（xi1，xi2，…，xip）；β（τ）=（β1（τ），β2（τ），…，βp（τ））′为p维τ分位数系数向量且β（τ）取决于τ。对第j个时刻的{yij，i=1，2，…，n；j=1，2，…}，可用简单优化问题的解将yij的经验条件分位数函数定义为：

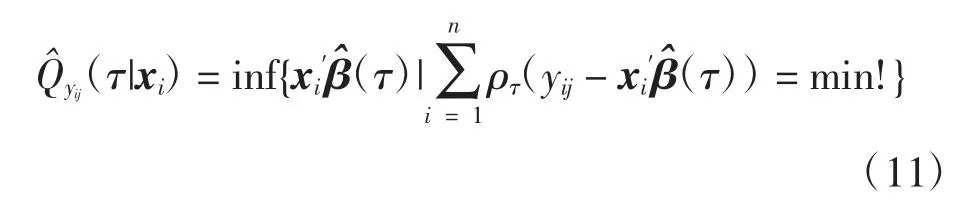
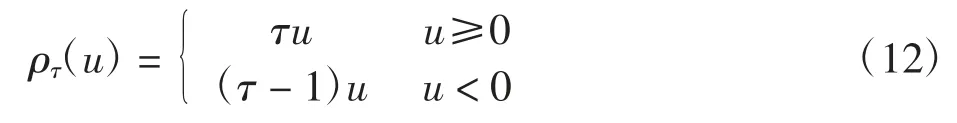
式中：u为观测值与其估计值的残差。

在模型（2）中通过对yij与xi′β的残差的估计损失和函数进行最小化求解可得β（τ）。假设R（τ）是最小化估计损失和函数，即：

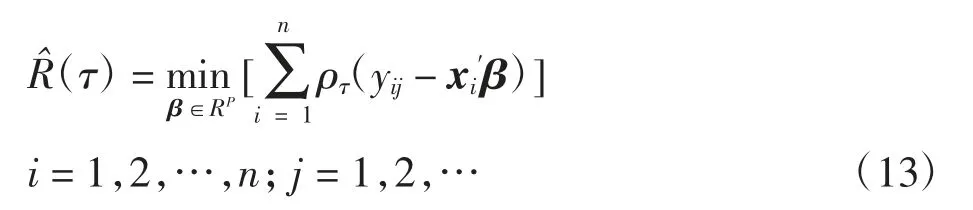
式（13）根据式（12）可写成：

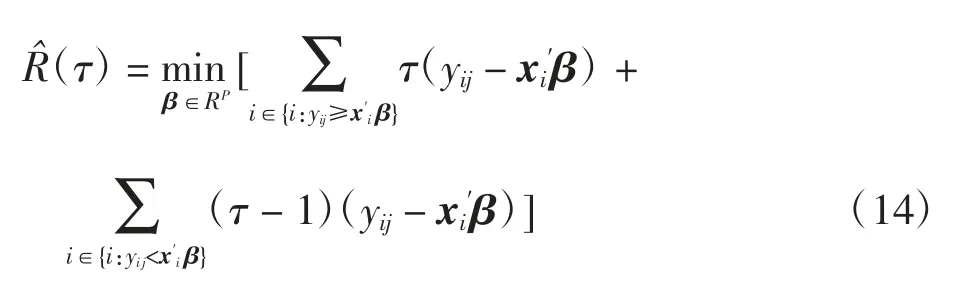
根据Koenker等[8-9]，式（11）于τ的左导数。可以通过单纯形法、内点法和平滑法等对式（14）进行求解

3 基于分位数回归方法的MEWMA控制图

对一般线性函数型模型基于分位数回归方法，结合MEWMA控制图，给出一种新的MEWMA控制图在线监控回归系数分位数。通过τ=0.5即中位数说明基于分位数回归方法建立MEWMA控制图。

根据式（2）和式（9），则yij的条件分位数函数也可以写成：

式中：Qεij（τ）为εij的τ分位数函数。

模型（2）中εij均是独立同分布于均值为0且方差为σ2的正态分布，则Qεij（0.5）=0；再根据式（10）可得β（τ）=β。假设εij的分布函数记作F（x），其概率密度函数记作f（x）。因为Qεij（0.5）=0，则F（x）的中位数为0，εij在中位数的概率密度为f（0）。根据Koenker等[5]定理，若σ2和f（0）相比满足条件[2f（0）]-1＜σ，则最小绝对误差估计（LAE）的渐近方差比最小二乘估计（LSE）的方差小；则LAE估计即回归中位数（（0.5））比LSE回归系数更有效。

当统计过程可控时，根据Bassett等[10]的定理可知的极限分布是正态分布；其均值为0且协方差阵为是来自F（x）的随机样本的样本中位数的渐近方差即ω=[2f（0）]-1。

对模型（2）在线监控p个回归系数中位数，给出新的MEWMA控制图。

式中：Zj为p维随机向量。当统计过程可控时，Zj服从均值为0且协方差阵为（Q*）-1的多元正态分布，其Q*=nQ。将MEWMA控制图统计量定义为：

式中：W0为p维初始向量。

若

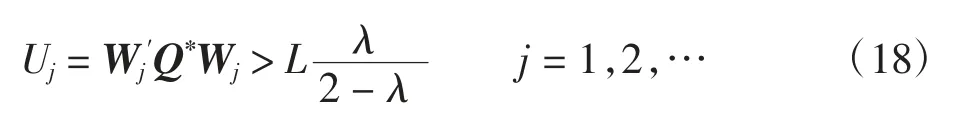
控制图就会报警。

4 模拟研究控制图表现

根据Qi等[11-15]理论，通过平均运行长度（ARL）研究本文推荐的MEWMA控制图监控表现。在可控模型中τ=0.5、0.9，n=4，p=2，λ=0.2，β0（0.5）=3，β1（0.5）=2，β0（0.9）=3，β1（0.9）=2，σ2=1和xi=2，4，6，8。在参数已知的前提下，考虑其MEWMA控制图的可控平均运行长度（IC ARL）大约为200。通过数值模拟得到失控平均运行长度（OC ARL），分析其MEWMA控制图监控表现。模型（2）中截距和斜率中位数及0.9分位数分别发生漂移时MEWMA控制图的ARL如表1所示。

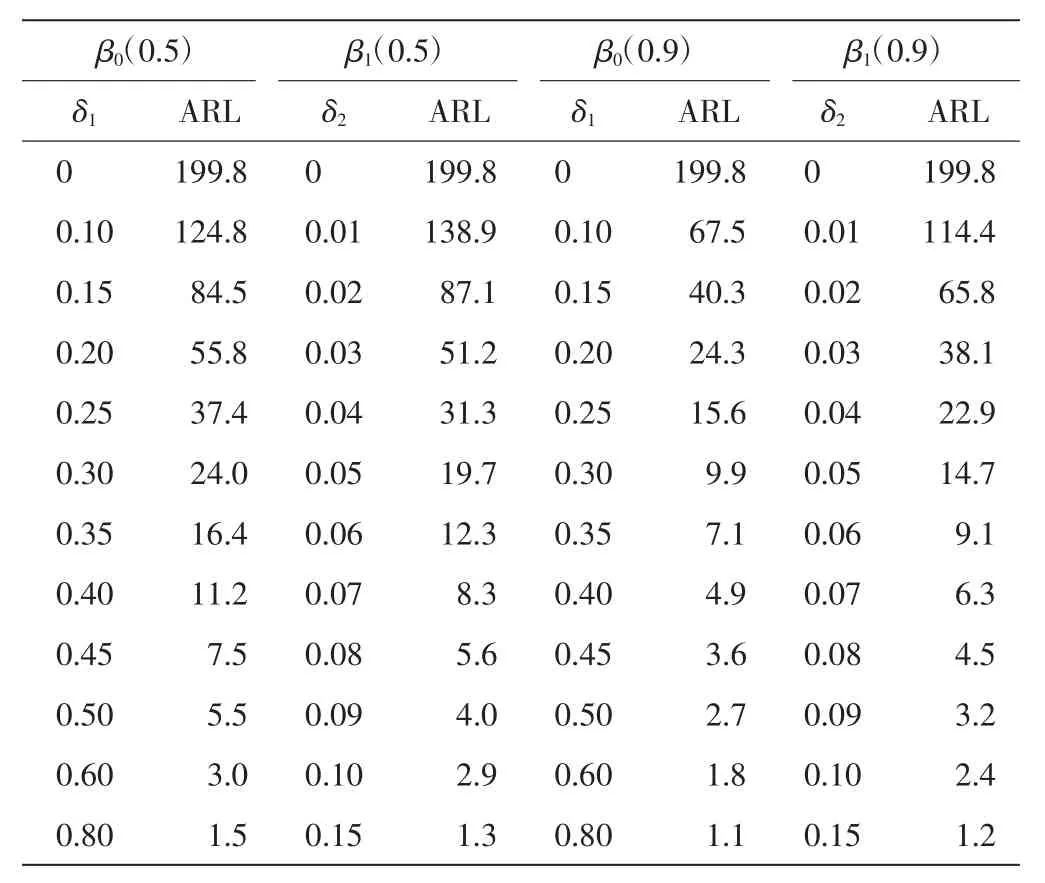
表1 模型（2）中截距和斜率中位数及0.9分位数分别发生漂移时MEWMA控制图的ARL

表1中，其MEWMA 控制图的IC ARL 为199.8，则将第I 类型错误概率控制在0.5%左右。在此基础上截距和斜率中位数分别发生漂移，即β（00.5）漂移到β0（0.5）+δ1σ 和 β（10.5）漂移到 β（10.5）+δ2σ；其0.9 分位数发生同样的漂移。截距或斜率中位数及0.9 分位数发生的漂移越大，其OC ARL 越小，则其MEWMA控制图探测漂移的速度越快。它们分别发生0.15、0.02小漂移的 OC ARL 分别是 84.5、87.1、40.3 和 65.8；分别发生 0.3、0.05 中等漂移的 OC ARL 分别是 24、19.7、9.9 和14.7；则其MEWMA 控制图可以有效地探测截距或斜率中位数及0.9 分位数发生的中小漂移。分别发生0.8、0.15 大漂移的OC ARL 都在2 步以内，则其MEWMA 控制图可快速探测到截距或斜率中位数及0.9 分位数发生的大漂移。分别发生0.1、0.01 小漂移的 OC ARL 分别是 124.8、138.9、67.5 和 114.4；使用渐近控制限而不是精确控制限，会导致其MEWMA 控制图探测漂移的速度推迟。模型（2）中截距和斜率中位数及0.9 分位数同时发生漂移时MEWMA 控制图的OC ARL 如表2所示。

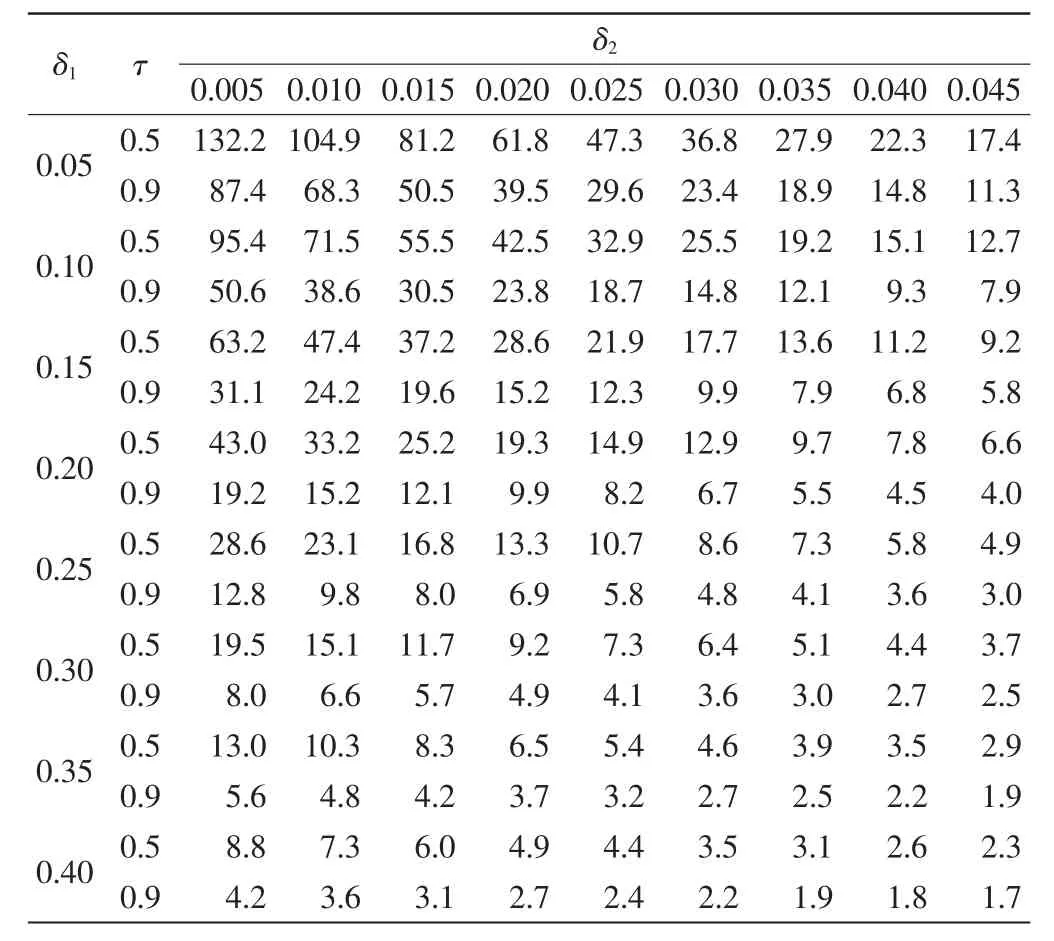
表2 模型（2）中截距和斜率中位数及0.9 分位数同时发生漂移时MEWMA 控制图的OC ARL

表2中，截距和斜率中位数及0.9 分位数同时发生漂移时，二者漂移同时变大或者任一个发生的漂移固定，另一个发生的漂移越大，其OC ARL 越小，则其MEWMA 控制图探测漂移的速度越快。它们同时发生0.1 和 0.01 小漂移的 OC ARL 是 71.5 和 38.6，同时发生 0.25 和 0.025 中等漂移的 OC ARL 是 10.7 和 5.8；则其MEWMA 控制图可以有效地探测截距和斜率中位数及0.9 分位数同时发生的中小漂移。同时，发生0.4和0.045 大漂移的OC ARL 是2.3 和1.7，则其MEWMA控制图可快速探测到截距和斜率中位数及0.9 分位数同时发生的大漂移甚至OC ARL 在2 步以内。