基于一维卷积神经网络的齿轮箱故障诊断研究

赵 璐，马 野

(海军大连舰艇学院 导弹与舰炮系，大连 116018)

0 引 言

传统的齿轮故障诊断大多采用信号处理手段提取出故障特征，再根据故障特征进行诊断.程军圣等[1]采用局部特征尺度分解方法进行齿轮故障诊断，并与经验模态分解、局部均值分解方法进行对比，证明此方法的优越性.但是提取故障特征需要复杂的信号处理技术，此方法具有提取特征阶段计算量大的缺点.

近年来，深度学习发展迅速，也被运用到故障诊断领域.刘秀丽[2]等提出一种基于深度信念网络的风电机组齿轮箱故障诊断方法，获得了比传统故障诊断方法更高的正确率；李东东等[3]提出了基于一维卷积神经网络和 Soft-Max分类器的风电机组行星齿轮箱故障检测模型，直接使用原始时域数据训练网络，取得了良好效果.但是一维卷积神经网络对齿轮复合故障的分类能力还有待探究.

针对上述问题，本文提出一种使用一维卷积神经网络进行轴承故障诊断的方法，并设计实验探究一维卷积神经网络识别齿轮各种故障时的分类能力.

1 一维卷积神经网络结构

一维卷积神经网络与二维卷积神经网络类似，其基本结构包括输入层、卷积层、池化层、全连接层和输出层，其中可设置多层卷积层和池化层[4]，提高网络性能.一维卷积神经网络结构如图1 所示.

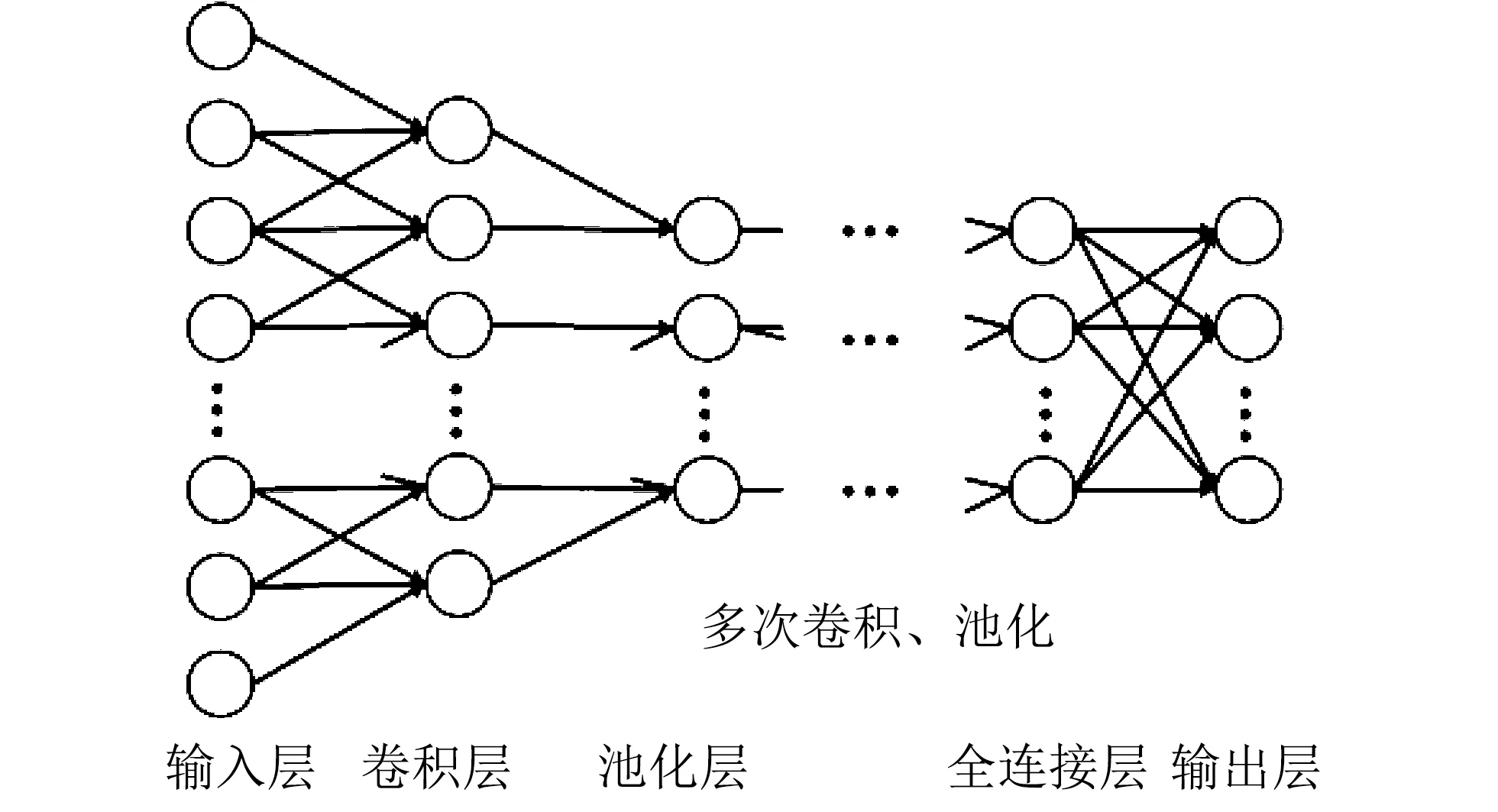
图1 一维卷积神经网络示意图Fig.1 Schematic diagram of one-dimensional convolutional neural network

卷积层通过卷积操作提取输入的特征，与数学上的卷积不同，卷积神经网络的卷积核是一个权值矩阵，卷积核对输入局部加权求和，卷积核以一定步长遍历一次输入得到卷积的输出.在卷积神经网络训练过程中，卷积核权值会不断调整优化，使其能更充分地提取特征.一维卷积操作如图2 所示，其中输入为一维数列，卷积核为一维，长度为3，卷积核移动步长为1.

图2 一维卷积操作示意图Fig.2 Schematic diagram of one-dimensional convolution operation

卷积后还可对输出使用激活函数提升卷积神经网络性能[5]，常采用ReLU激活函数.同时还可以采用多个卷积核进行训练，提高网络性能.卷积核遍历输入时地步长决定输出个数，其关系为

(1)

式中：cin表示输入数据个数；cout表示输出数据个数；cwindow表示卷积核大小；cinterval表示卷积核移动步长.可以看出，步长越大，输出数据个数越少，减小了后续网络计算量.

卷积层后通常连接一个池化层，与卷积操作类似，池化操作也有池化核大小核步长两个参数，池化核以一定步长遍历输入，按池化方法得到池化输出.常见的池化方法有最大池化、最小池化、平均池化、随机池化等[6]，其中最大池化提取最大值，适用于分离非常稀疏的特征[7].若池化步长与池化核大小一致，则是无重叠池化，若池化步长小于池化核大小，则是重叠池化.一维池化操作如图3 所示，输入为一维数列，池化核大小和池化步长均为3,采用最大池化.

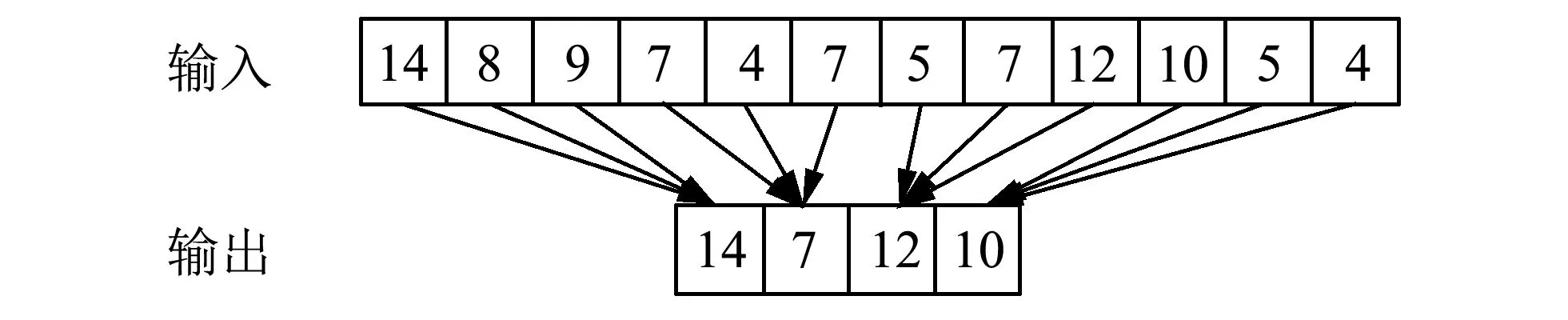
图3 一维池化操作示意图Fig.3 Schematic diagram of one-dimensional pooling operation

与卷积操作类似，池化核大小和池化步长决定输出个数，对于无重叠池化，其关系为

(2)

式中：pin表示输入数据个数；pout表示输出数据个数；pwindow表示池化核大小.池化起到二次提取特征的作用，进一步降低网络计算量.

在经过多次卷积池化之后，采用全连接层对卷积池化结果进行分类[8].全连接层每个神经元与前一层所有神经元进行全连接[9]，常采用ReLU激活函数.全连接层的输出值传递到输出层，输出层激活函数通常是softmax函数，将输入转化为和为1的概率分布.输出层也可以采用tanh函数进行归一化.为减小神经网络计算量，使其快速收敛，在全连接层和输出层常采用随机梯度下降法和小批量梯度下降法进行权值更新[10].为防止训练过拟合，在全连接层常采用丢失数据(dropout)技术进行正则化，提高其对测试集的分类性能[11].

2 实验方案设计

2.1 实验数据构造及描述

实验数据采用QPZZ-II旋转机械振动分析及故障诊断实验平台系统[12]的部分数据.实验用齿轮有点蚀、磨损、断齿3种故障，通过大小齿轮施加不同故障共有正常、点蚀、磨损、断齿、断齿加磨损和点蚀加磨损6种状态.在实验平台不同位置设置传感器监测转速、负载、位移、加速度等参数，采样频率均为 5 120 Hz，驱动电机转速为880 rpm.本次实验采用制动力矩0.2 A下输入轴负载侧轴承Y方向的加速度检测数据，原始实验数据点数约为53 000个.

因电机每转约采集400个数据，使每个样本数据长度大于电机一转采集的数据长度，故设置一维卷积神经网络输入样本长度为1 024.因原始数据长度有限，正常截取样本时训练集样本数过少.为增强网络性能，采用训练集增强技术，有重叠地截取训练集样本，重叠长度为100个数据，每个原始数据可截取250个训练样本.训练集截取后，剩余部分原始数据分割为测试集，测试集样本长度1 024，测试集样本数最多可截取25个.截取后各种故障样本波形如图4 所示，可以看出，样本波形含有较多噪声，常规手段很难分清每一种故障.

图4 样本波形示意图Fig.4 Sketch map of sample waveform

获得不同故障的训练样本和测试样本后进行归一化处理，归一化公式为

(3)

式中：x表示原始数据，xnorm表示归一化后的数据，xmax和xmin表示原始数据的最大值和最小值.

根据故障类型，为探究一维卷积神经网络对不同故障的分类能力，设置4组实验.第1组实验探究神经网络对齿轮箱是否存在故障的分类能力；第2组探究神经网络对单独发生的故障的分类能力；第3组实验探究神经网络对复合故障的分类能力.各个实验所用训练集测试集样本数如表1 所示.

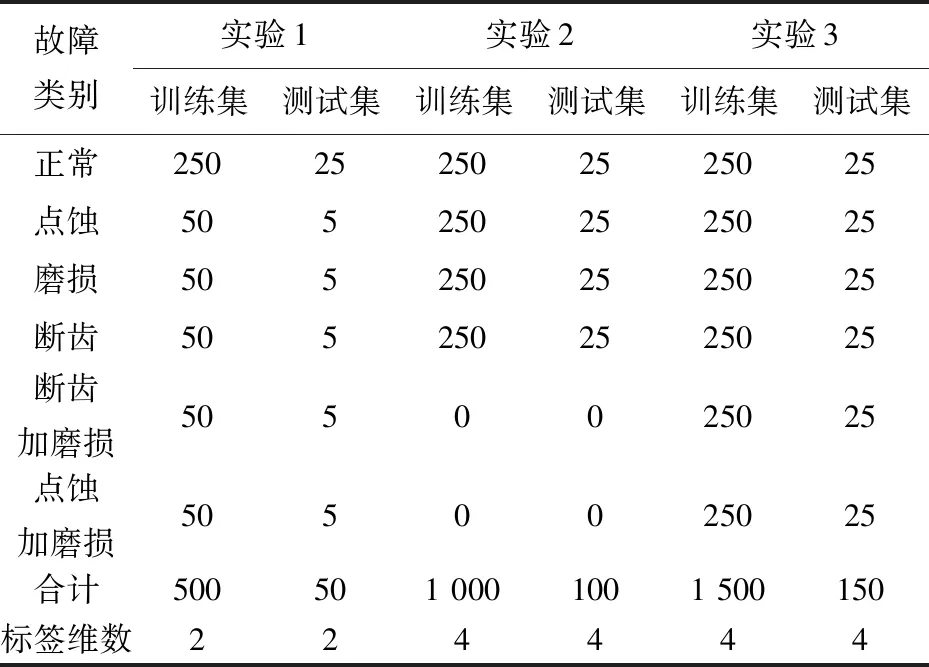
表1 各组实验所用样本数Tab.1 The number of samples used in each group

2.2 一维卷积神经网络参数设置

根据上文对一维卷积神经网络结构的介绍，多层卷积池化可提升网络性能，但是由于样本长度限制，采用3层以上卷积池化层时，最后一层池化层的输出维数可能小于标签维数，会极大降低网络性能，故设计具有3个卷积池化层的一维卷积神经网络.全连接层采用ReLU激活函数，前两个实验输出层采用softmax激活函数，第3组实验因标签含有多个1，故输出层采用tanh函数.根据张伟[13]的研究，第1层卷积采用大卷积核能取得较好的训练效果，故第1层卷积核大小为64，其余各层卷积核池化核大小均为4.为控制变量，全连接层神经元个数与第3层池化输出维数一致，输出层神经元个数与标签维数一致.为使结果具有较大差异便于比较，卷积层未采用激活函数，网络各层均未采用dropout.为加快训练速度，采用Adam算法更新权值，设置学习率为0.001，同时采用小批量梯度下降法，批量大小为200.网络各层输出维数如表2 所示.

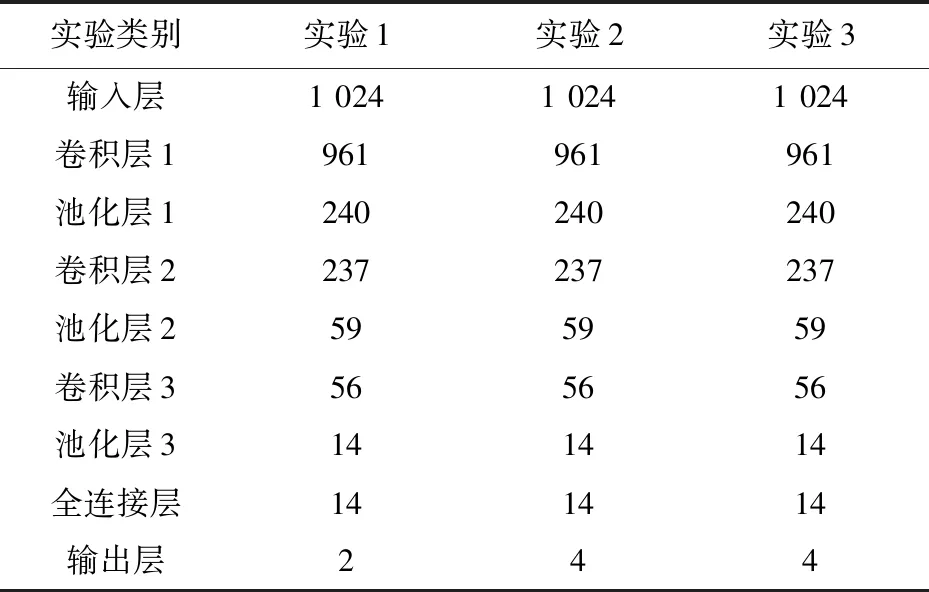
表2 各个网络层输出维数Tab.2 Output dimension of each network layer

2.3 实验过程

实验过程基于TensorFlow的深度学习库，采用Keras高层神经网络API，采用Anaconda的Jupyter Notebook作为python编译器.将训练集输入卷积神经网络进行训练，迭代500次后终止训练，得到训练过程中损失函数变化曲线.之后将测试样本输入训练好的网络，获取测试样本输出.

因输出层采用softmax激活函数，故将测试集输出中的最大值所在位置与标签中1的所在位置进行比较，一致则分类成功，否则分类失败，统计对每类故障的正确分类数以及总的分类正确率，实验重复3次.

3 实验验证及分析

3.1 训练过程分析

对3组不同实验，各取其中1次的训练过程绘制误差收敛曲线如图5 所示.

图5 训练过程误差收敛曲线Fig.5 Loss function value of training process

可以看出，训练集迭代500次后，3组实验损失函数均下降到较小的值，无需继续增加训练次数，训练结果可用于在测试集上测试.此外，对比3组实验，随着故障种类的增多，损失函数下降速度变慢，可以预见当原始数据集继续增加故障种类时，需要增加迭代次数来提高网络性能.

3.2 测试集分类结果分析

测试集分类结果如表3所示.第1组实验，一维卷积神经网络可以准确地诊断出齿轮箱中是否存在故障；第2组实验，网络也比较准确地诊断出齿轮箱的单一故障类型，其中3次实验对正常和点蚀状态诊断均存在诊断错误，但是诊断错误率很低；第3组实验，继续增加故障类别后，诊断正确率进一步下降，其中对点蚀和断齿的诊断存在较严重的错误.通过对样本波形的观察，可以看出正常、点蚀和断齿波形有较多相似之处，均有一定的周期性，这可能是点蚀和断齿诊断错误较多的原因.

若要进一步提高故障诊断准确度，可采用增加样本数、增加训练迭代次数、训练过程中采用正则化和多次诊断结果融合等手段.以多次诊断结果融合为例，对于测试集25个样本，若诊断出存在某个故障的样本数大于13，则认为存在此类故障，则第3组实验均正确诊断出了复合故障.

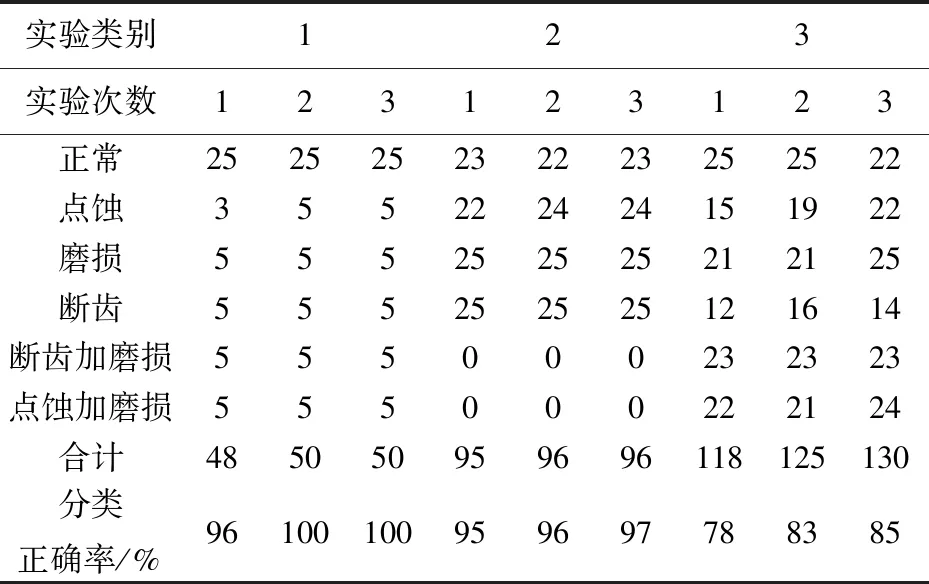
表3 测试集分类结果Tab.3 Classification results

4 结 论

针对基于一维卷积神经网络的齿轮箱故障诊断，设计实验探究卷积神经网络对不同故障的分类能力.实验结果表明，一维卷积神经网络能准确区分齿轮的故障与正常状态，较为准确地分类出单独故障，对于复合故障分类能力下降.可采用增加样本数、增加训练迭代次数、训练过程中采用正则化多次诊断结果融合等手段进一步提高诊断准确度，为使用一维卷积神经网络对齿轮类故障诊断提供理论依据.