考虑管壁导热的方管内熔盐混合对流传热数值模拟

杨岑玉，孟 强，王 乐，陈梦东，胡 晓，徐桂芝

（全球能源互联网研究院有限公司，先进输电技术国家重点实验室，北京 102209）

能源是人类生存和发展的物质基础，是经济和社会发展的重要资源。进入21世纪以来，能源需求逐年旺盛，能源供应形势趋于紧张，能源资源正度越发激烈[1]。化石燃料仍是全球能源消费的主要构成，并导致越来越严重的问题。寻找替代能源既可以解决、缓解化石能源短缺，又可以避免因化石能源燃烧导致的生态环境恶化。

可再生能源在满足能源需求、改善能源结构、减少环境污染等方面起到了巨大作用。太阳能在全球绝大部分地区普遍存在，并且利用方式多样，为常规能源缺乏的国家和地区提供解决能源问题的理想选择。太阳能热发电是太阳能利用的重要形式之一，可与大规模低成本蓄热系统相结合，并且系统中的热功转换部分可采用常规火力发电机组，技术成熟、发电平稳、可控输出，符合发电方式的基本要求，是理想的发电技术。太阳能热发电技术可产生大量电能，是最有可能代替传统能源方式的可再生能源利用方式之一[2]。

典型的太阳能热发电系统主要由聚光集热子系统、蓄热子系统、热动力发电子系统等主要部分能够成[3]。太阳能在利用过程中具有间歇性，太阳辐射受到昼夜条件以及天气变化等的影响，为了保证整个系统在满足功率要求的情况下平稳运行，系统必须依靠储存的太阳能来维持正常运行。因此，蓄热子系统是太阳能热发电系统中必不可少的重要组成部分。

熔融盐因为具有适用温度范围广、使用压力低、导热性能好、比热容大、黏度较低、热稳定性高、安全易得、价格低廉等优点受到广泛关注[4-6]，目前熔融盐作为传蓄热工质已经在太阳能热发电领域得到了应用[7]，并取得了显著效果。美国Solar Two电站将熔融盐作为新的传蓄热介质应用于太阳能热发电系统中，其使用1440吨混合熔盐(60%NaNO3+40%KNO3，质量分数)作为传蓄热工质，实现了105MW∙h的蓄热能力，折合3小时的汽轮机满负荷运行[8]。西班牙Gemasolar[9]19MW塔式熔盐传热太阳能热电站于2011年建成运行，总计使用8500吨混合熔盐，具备24小时连续发电能力，年运行小时数达到6500小时，年发电量为1.1亿度电。同年，西班牙建成了采用二元混合硝酸盐作为蓄热工质的Arcosol 50电站，实现了7.5小时的蓄热能力。2012年西班牙又建成了基于熔盐蓄热的50MW商业运行电站Aste 1A、Astexol II，实现了8小时的蓄热时长[10]。

熔融盐对流传热特性对传热设备的设计具有指导意义，并且决定着太阳能热发电的效率，得到了国内外学者的关注。美国橡树岭国家实验室的HOFFMAN对电加热情况下的NaOH、Flinak（NaF、LiF、KF混合物）、三元混合硝酸盐Hitec在圆管内对流换热情况的进行了研究，并认为该混合熔盐在换热设备中用作传热流体时，可 用MCADAMS，DITTUS和BOELTER以 及COLBURN提出的标准关联式进行设计[11]。20世纪80年代，ALLMAN等[12]对熔盐强化传热进行了研究，其研究了熔盐在异型管蒸气发生器中的换热。吴玉庭等[13-14]对圆管内硝酸盐的强制对流传热特性进行了实验研究，并拟合了实验关联式。在此基础上，特别研究了横纹管内熔盐强制对流传热特性和流动特性，得到了换热和阻力的无量纲准则关联式，评价了横纹管的综合强化传热效果。

在熔盐实际利用过程中，存在非均匀加热，固体表面和流体间存在温度差异，由密度梯度导致浮升力效应，进而与主流方向流动过程叠加形成混合对流。国内外许多研究者对空气、水、非牛顿流体、纳米流体等多种工质在不同管路通道内的混合对流传热过程进行了研究，发现了混合对流过程中流型以及传热特性的变化，对混合对流过程中强化传热的原因进行了分析，但是目前国内外针对熔盐混合对流传热的研究很少。另外，管壁导热会对熔盐混合对流传热过程产生一定的影响。本文数值模拟研究了考虑管壁导热影响的熔盐混合对流传热过程。对水平方管单面加热时的壁面温度、传热系数以及无量纲参数的变化规律进行了模拟研究，并将结果与流型判定图和经典关联式进行对比，进而分析了熔盐混合对流传热特性。

1 模型建立

1.1 模型控制方程

（1）质量守恒

连续性方程：流体在流动过程中满足质量守恒定律，控制体内单位时间的流体净流出质量总和等于其因密度变化而减少的质量，方程表述如下

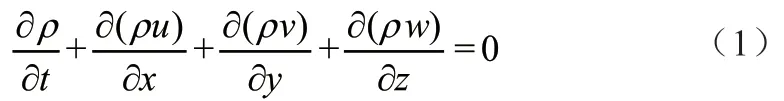
本文视流体流动过程为不可压缩流动，方程可进一步简化为

式中，u、v、w分别为x、y、z方向上的速度分量；ρ为密度；t为时间。

（2）动量守恒

根据牛顿第二定律，给定的流体微元的动量/时间变化率等于在其上各种外界作用力之和。针对本课题的模拟过程，流动过程仅受重力作用，表述如下：

（3）能量守恒

根据热力学第一定律，微元体中能量的增加率与进入微元体的净热流通量及质量力与表面力对微元体所做功之和相等，模拟过程中忽略由黏性耗散导致的加热源时，可简化为

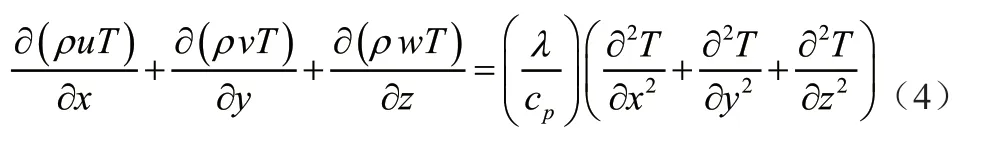
式(4)中，λ是流体导热系数，cp是定压比热容，T是温度。

固体壁面导热遵循能量守恒定律和傅里叶定律，可得导热微分方程为

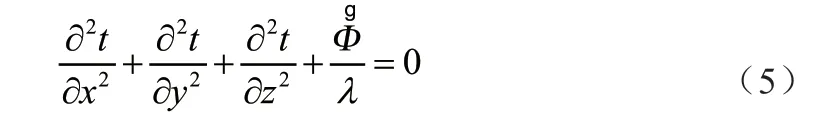
本文采用FLUENT软件的双方程RNGκ-ε模型，对熔盐混合对流进行数值模拟。双方程κ-ε模型为目前使用最为广泛的湍流模型，原标准κ-ε模型忽略了漩涡的影响，RNGκ-ε模型就此对其进行了改进，并给出了普朗特数的一个解析式，且对低雷诺数流动黏性情况下提供了解析公式，由此提高了适用范围和计算精度，非常适用于主要影响因素为浮升力二次流影响的熔盐混合对流模拟过程。

因此，在实际计算过程中，还需附加湍流输运方程

式中，Gk是由平均速度梯度引起的湍动能产生；Gb是由浮升力影响引起的湍动能产生；YM为脉动膨胀对总耗散率的影响；αk、αε分别为湍动能和耗散率的有效普朗特数的倒数；μ为黏度，μt为湍流黏性系数。C1ε、C2ε、C3ε为经验常数，软件中默认为常数，σk、σε分别为湍动能k与耗散率ε默认值。

1.2 几何模型

对熔盐在水平方管内的流动和传热过程进行模拟，考虑壁面导热影响，重力方向沿y轴向下，方管管宽为19mm，管长为1000mm，壁厚为3mm，方管几何模型如图1所示。数值模拟的边界条件包括：入口边界流速与温度；出口边界设定为常压；方管壁面没有滑移，全浮升力效应设置为开启；壁面为定热流密度加热方式；考虑壁面导热；FLUENT计算模型采用双方程RNG，κ-ε计算模型；判断收敛的条件为残差值10-6～10-8，迭代次数为10000次，求解过程中所有结果均达到收敛。

1.3 混合熔盐物性参数

混合熔盐由于具有高热稳定性，工作温度宽，价格低等优点，在光热发电和核能领域中作为传热工质应用广泛。本文流体工质选用Hitec混合硝酸盐 (NaNO3-NaNO2-KNO3，7%-40%-53%)，其参数包括熔点142℃，沸点680℃。

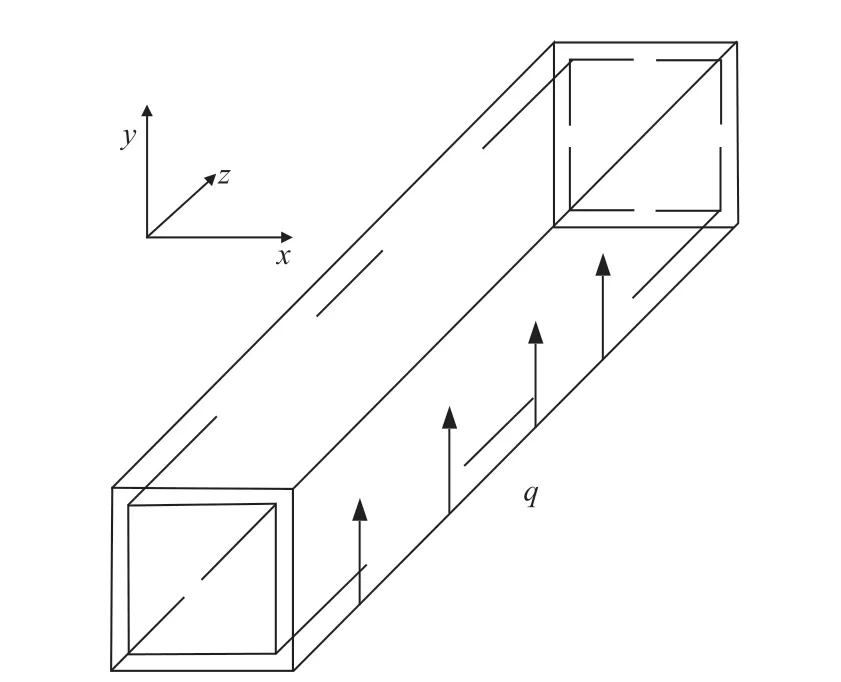
图1 方管几何模型Fig.1 Geometry of sqaure tube

由于熔盐为新型工质，FLUENT材料数据库中无法提供，因此需要编写UDF（User-Defined Function）对熔盐材料进行补充。UDF为FLUENT软件提供的一个用户接口，可采用C语言编写的方式对Fluent模块数据进行补充。

Hitec熔盐的主要物性参数为：①密度 （熔化后液态区间内）：ρ=2287.7993-0.7484T；②定压比热容 （熔化后液态区间内）cp=1507-0.1T；③导热系数 （熔化后液态区间内）λ= 0.8099-7.827×10-4T+1.043×10-7T2；④动力黏度：μ= 0.06284-2.253×10-4T+2.7903×10-7T2-1.1738×10-10T3；

固体壁面材料为不锈钢（steel），物性参数如下： 密度ρ=8030kg/m3；定压比热容cp=502.48J/(kg∙K)；导热系数λ=16.27W/(m∙K)。

1.4 验证边界条件与网格划分的无关性

研究中采取对模型进行共5种网格划分的方法来检验仿真实验结果与网格划分的无关性，如图2所示。不同网格的仿真结果显示当网格数量≥25×25×1000时流体温度的一致性较好，其他较小的网格划分的偏差较大。因此，本文在综合考虑计算准确度与消耗时间后，采用了25×25×1000的网格划分。

2 模拟结果

2.1 模型验证

图2 网格无关性验证Fig.2 Grid independent validation

研究中对模拟结果的可靠性进行了判定，模拟结果处于湍流混合对流区域内。为进一步验证结果的准确性，本文将模拟结果与前期获得的实验结果进行了对比。实验流程图如图3所示。实验过程中通过对方管测试段进行底面非均匀加热，使得熔盐在流动过程中产生浮升力效应进而形成混合对流过程，通过测量系统对各部分温度进行记录，结合熔盐流量、非均匀加热热流密度等已知参数进一步计算熔盐换热系数、对应的相关无量纲参数等，并通过对熔盐泵和加热器等设备的调节，以达到不同工况的情况，获得其变化规律，进而得到水平方管内底面加热情况下熔盐混合对流传热特性。模拟结果与实验结果对比情况如图4所示。可以从图中看出模拟结果与实验结果符合程度较为良好。考虑壁面导热模拟结果与实验结果更为接近，偏差在±10之间。该验证结果一方面对于熔盐在非均匀加热过程的流动方式为混合对流进行了验证，另一方面对于模拟过程所选用的计算模型的可靠性进行了确认。

2.2 流动特性

图5为方管单面加热工况为加热热流密度200 kW/m2，轴向流速达到0.3 m/s，主流方向上z=100 mm处的横截面速度分布。

从图5的流速分布图中可以看出外框蓝色部分为管壁壁厚区域，三种加热方式与不考虑壁面导热的结果[15-16]趋势相同，均呈现出主流核心区的流速相对较高，且流速分布从中心向四周逐渐降低的趋势。与不考虑壁面导热的模拟结果[15-16]流动特性相比，可以看出考虑壁面导热结果流速分布相对更加均匀。从三种加热方式流线分布图中可以看出，底面加热和侧面加热方式同样也产生了可观的涡流，顶面加热方式流线向核心区汇聚，产生了涡流形成的趋势。产生涡流的原因是由非均匀加热所引起的浮升力现象造成，由于考虑壁面导热，在非均匀加热过程中，热量会通过壁面导热方式从加热面迅速向非加热面传递，非均匀加热的效果弱于不考虑壁面导热的结果，温度分布以及流线分布上所体现出的结果从程度上来说相对较弱，但是这样的结果更加符合现实应用中的情况。

图3 熔盐混合对流传热实验原理图Fig.3 Schematic of molten salt mixed convection experiment

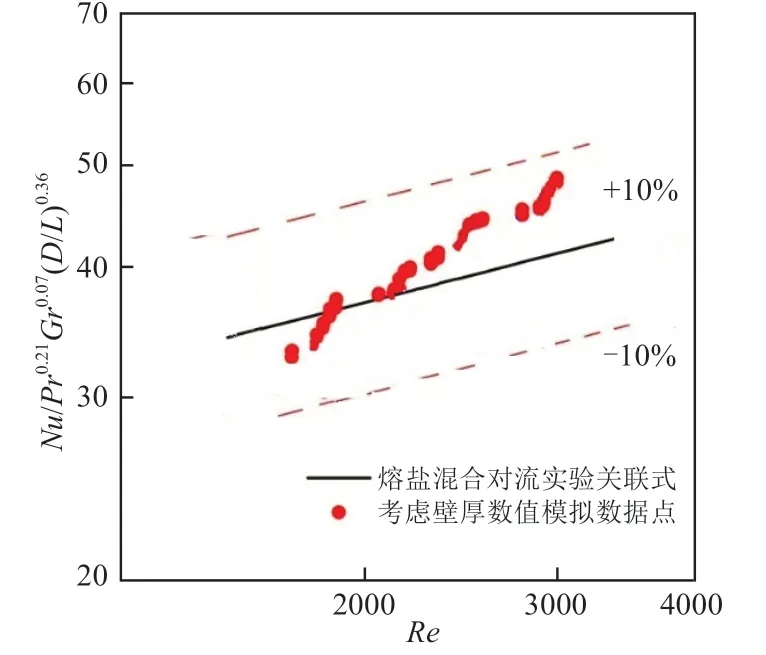
图4 实验结果与数值模拟结果对比图Fig.4 Comparison between the simulated data and experimental data

图6为方管单面加热工况为加热热流密度200kW/m2，轴向流速达到0.3m/s，主流方向上z=500mm处的横截面速度分布图和流线图。

从图6可看出流速基本已经发展稳定，并形成了稳定涡流。其中，底面加热情况下产生了两个涡流，侧面加热情况下产生了一个涡流，顶面加热产生了两个涡流。不考虑壁面导热的模拟结果显示，顶面加热产生了四个涡流：两个涡流位于上部，靠近顶部加热面，是由非均匀加热浮升力现象产生；另外两个涡流位于截面下部，靠近壁面，是由于顶面加热过程中失稳现象所造成[15-16]。在考虑壁面导热的模拟结果中，由于温度通过导热方式迅速向壁面传递，因此由于顶部非均匀加热所产生的失稳现象不复存在，由其造成的截面下部的涡流也进而消失，只剩下由混合对流浮升力现象所产生的两个靠近加热面的涡流。

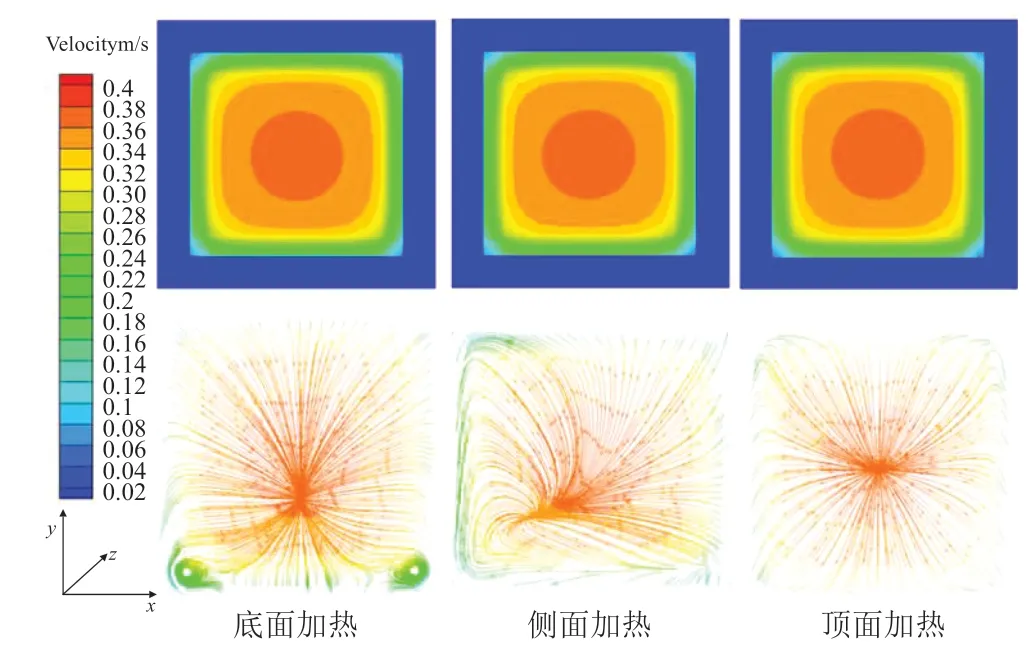
图5 z=100时的速度分布Fig.5 Velocity distributions at z=100

2.3 传热特性

图7为底面加热方式，加热热流密度为200 kW/m2，轴向流速达到0.3 m/s，主流方向各横截面处的温度分布情况。

从图中可看出，由于考虑了壁面导热，热量迅速从加热壁面向各壁面传递，使得各壁面温度迅速上升，进而可以对近壁面处的流体进行加热，从而产生这种类似尖状的温度分布，流体的温度分布结果相比于不考虑壁面导热结果更加均匀，整体的结果与不考虑壁面导热的模拟结果保持相同，温度随流动过程的深入呈上升的趋势。原因同样在于混合对流过程中所产生的浮升力效应，在两底角位置处的涡流对流动过程产生了扰动，加强了流体传热能力，因此呈现出尖状分布的特点，另外随着流动过程的深入，流体温度在加热面的持续加热下稳步上升，壁厚处的温度也由于导热的存在逐渐上升，相比于不考虑壁面导热的结果，考虑壁面导热的结果温度分布更加均匀。

图8为侧面加热方式，加热热流密度为200 kW/m2，轴向流速达到0.3 m/s，主流方向各横截面处的温度分布情况。如图7所示，由于存在壁面导热，热量传递速度更加迅速，温度分布更加均匀，热量不再是单一的从加热壁面像近壁面流体传递，而是首先通过导热传递到各壁面，进而传递给流体。左侧加热面温度明显高于其他壁面，因此近壁处的流体温度高于其他区域，温度差的存在使得流体内部产生密度梯度，进而产生浮升力效应，在混合对流过程中对流动过程和传热过程产生影响。

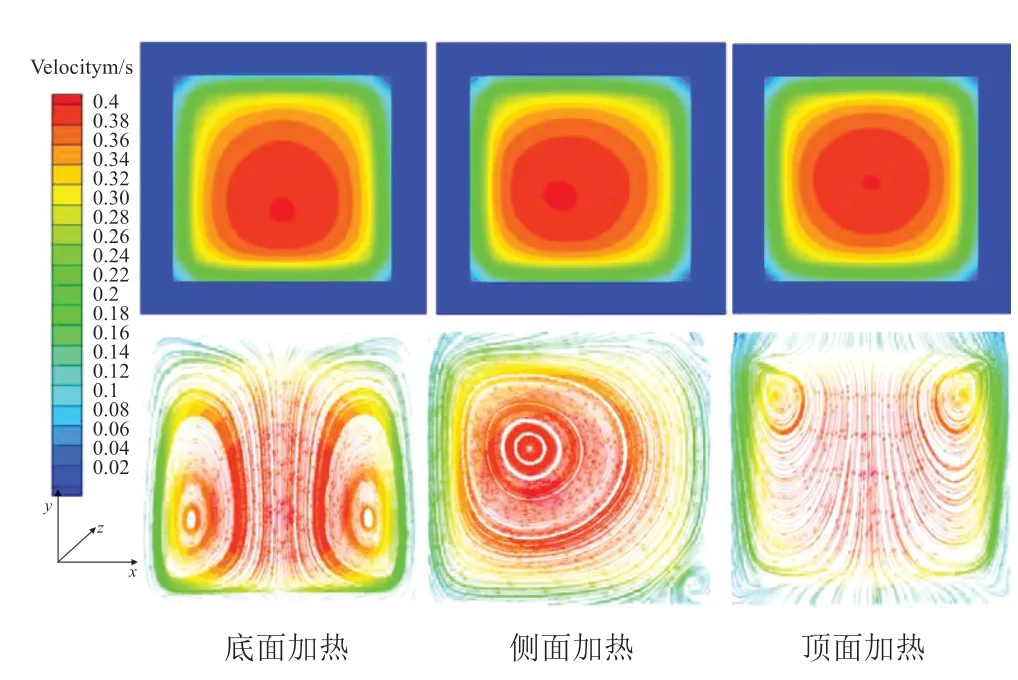
图6 z=500处速度分布Fig.6 Velocity distributions at z=500

图9为顶面加热方式，加热热流密度为200kW/m2，轴向流速达到0.3m/s，主流方向各横截面处的温度分布情况。如图8所示，壁面导热的存在使得在顶面加热过程中，温度的分布更加均匀，产生了两个由浮升力现象所产生的靠近顶部加热面的涡流。由于顶部涡流的存在，两顶角处流体的温度相对其他区域温度更高，这正是由于混合对流过程中所产生的涡流对流体传热过程进行强化的体现。

2.4 无量纲参数变化关系

2.4.1Nu数随Ri数的变化规律

图10～图12为3种方式情况下，不同位置处的局部Nux数随Ri数的变化规律。从3幅图中曲线的变化情况中可以看出，局部Nux数随流动过程的深入呈现出先减小后增大的趋势，当局部Nux数降到最低点后，随无量纲长度的增加而增长。原因在于入口段热边界层厚度迅速增长，导致流体的局部传热能力不断下降至最小值，随着加热过程的发展，流体内部产生密度差，在浮升力效应的影响下产生涡流，增强了传热效果，因此局部Nux数持续上升。

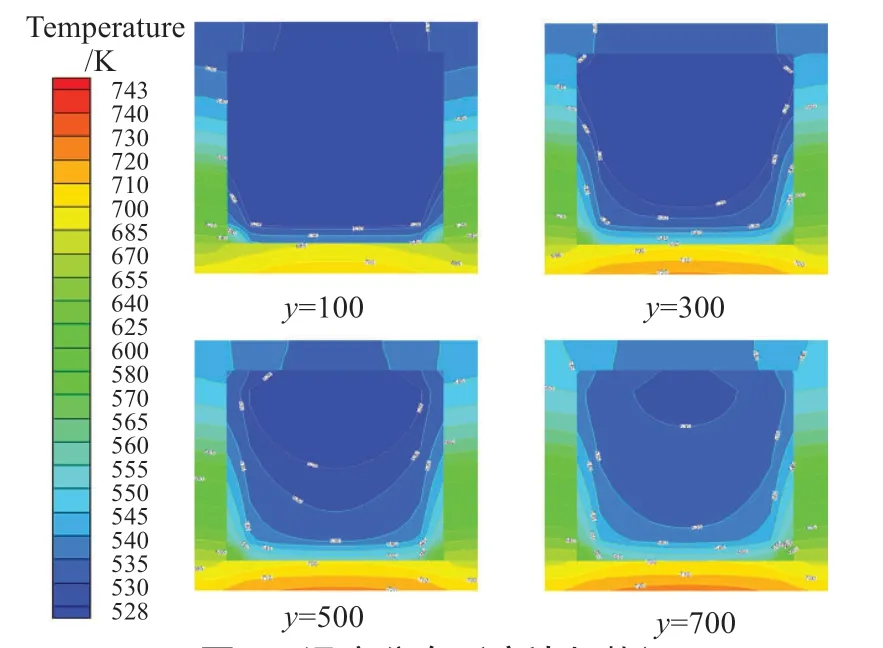
图7 温度分布（底边加热）Fig.7 Temperature distributions (bottom heated)

图8 温度分布（侧边加热）Fig.8 Temperature distributions (one side heated)

2.4.2 局部Nux数随Re数的变化规律

图13为底面加热热流密度为200kW/m2时，不同位置处的局部Nux随Re数的变化规律。从曲线走势可以看出，Re数越大，Nux越大，与Nux随Ri数变化规律相同，且同样是先减小至最低点后增大。Re数是表征流体流速的无量纲参数，即混合对流过程中入口流速越大，局部传热能力越强。侧面和顶面加热情况变化规律与底面加热情况结果相同。

2.4.3Ri数随Re数的变化规律

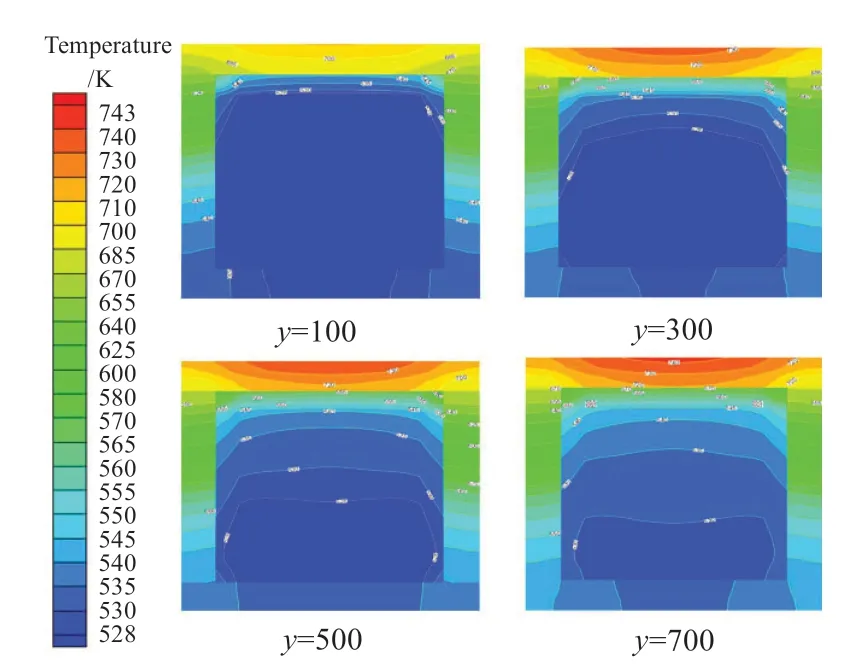
图9 温度分布（上方加热）Fig.9 Temperature distributions (top heated)

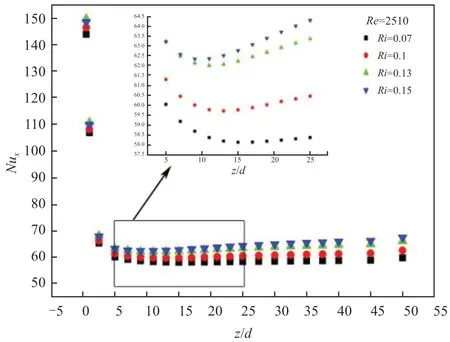
图10 局部Nux随Ri数变化规律（底面加热）Fig.10 The relationship between local Nusselt number and Richardson number (bottom heated)

图11 局部Nux随Ri数变化规律（侧面加热）Fig.11 The relationship between local Nusselt number and Richardson number (lateral heated)

图12 局部Nux随Ri数变化规律（顶面加热）Fig.12 The relationship between local Nusselt number and Richardson number (top heated)

图14为Re数和Ri数之间的影响关系，将图中的曲线纵向对比可知，相同工况下，Re数越大，Ri数越小。原因在于Re数越大，流体流速越大，混合对流过程中受迫对流的影响越大，自然对流的影响越小，流动过程类型偏向受迫对流，Ri数因此减小。将图中的去向横向对比可知，相同入口温度下，加热热流密度越大，Ri数越大，Re数越大；相同加热热流密度下，流体入口温度越高，Re数越大，Ri数越小。原因在于非均匀加热热流密度越大，浮升力效应越明显，混合对流过程强度越大，Ri数越大，同时熔盐物性参数随温度变化而变化，对Re数产生影响。而流体入口温度越大，流体与加热壁面间的温度差就会越小，进而浮升力效应所带来的影响变小，Ri数变小。

2.5 壁面导热对混合对流过程的影响

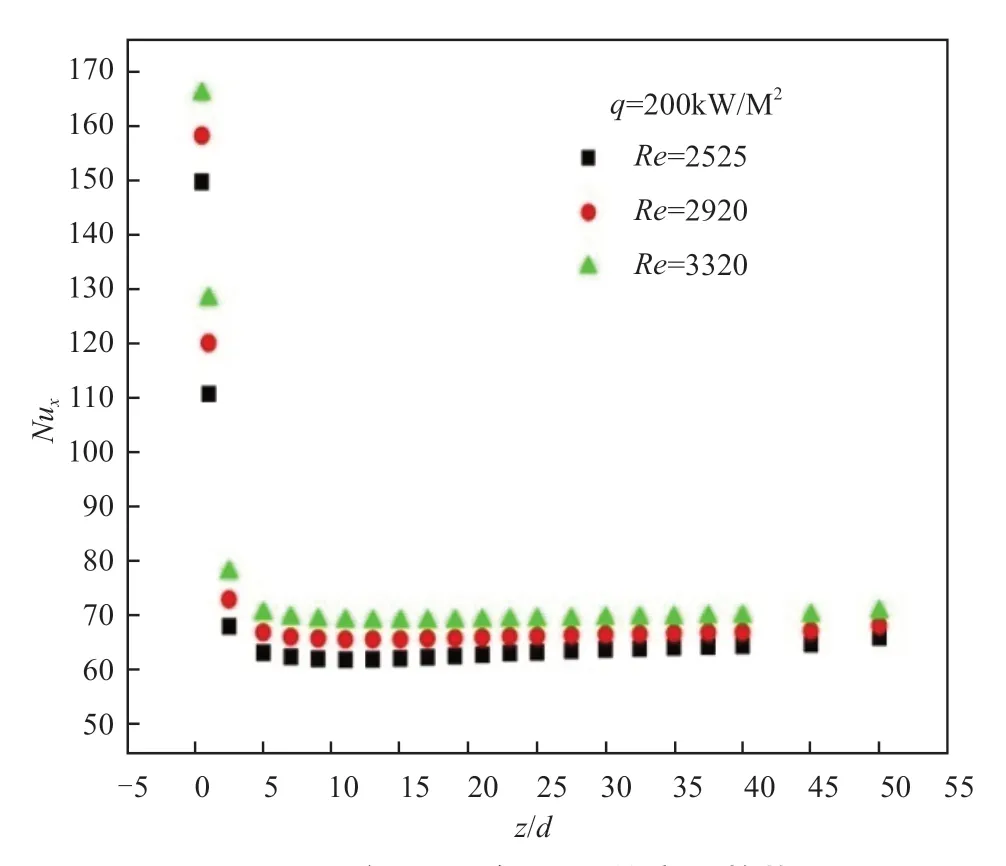
图13 局部Nux随Re数的变化趋势Fig.13 Changes of local Nusselt varied with z/d under different Reynold number

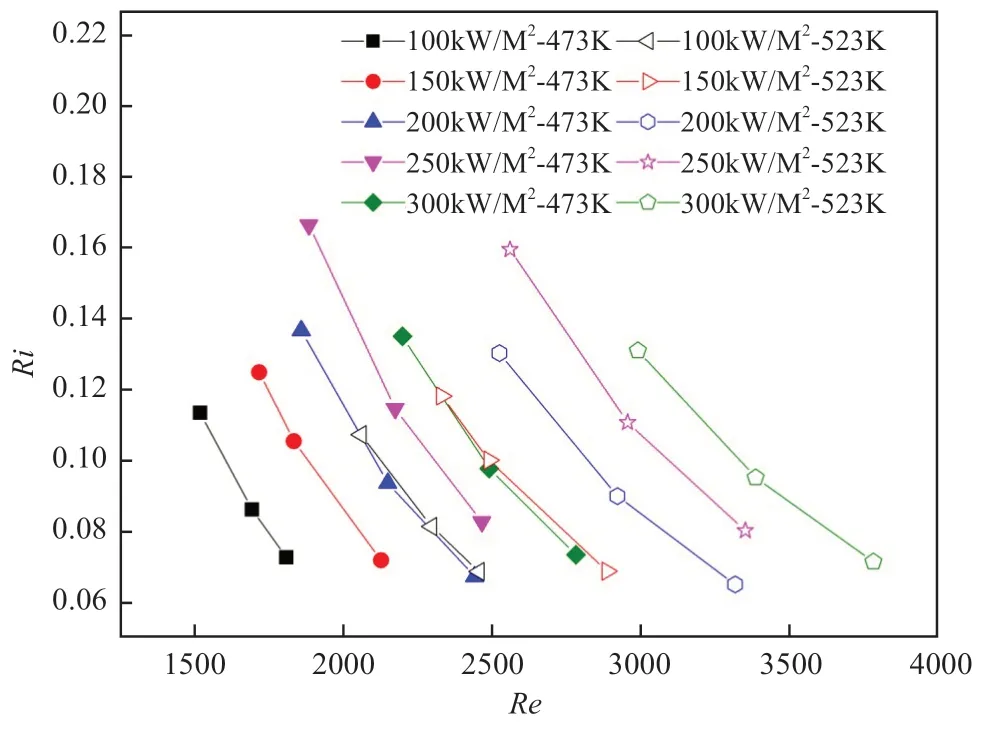
图14 Ri数与Re数间的变化关系Fig.14 The relationship between Richardson number and Reynold number

图15描述了壁面导热对局部Nux的影响关系。从图中可看出考虑壁面结果与不考虑壁面导热结果[15-16]所得出的规律基本一致，侧面加热情况所体现出的传热能力最强，顶面加热结果最弱。原因是由于各加热方式产生了不同数量和不同规格的涡流，涡流的存在对传热过程产生了影响。与不考虑壁面导热结果相比不同之处在于考虑壁面导热结果的局部Nux均高于忽略壁面导热的计算结果；且考虑壁面导热的计算结果局部Nux回升的位置均要早于忽略壁面导热的结算结果。这是因为壁面导热的存在使得温度分布更加均匀，入口段热量的堆积造成壁面温度与流体温度的温差低于忽略壁面导热的结果，从而使得局部Nux更高，增强了换热效果,进而局部Nux的最小值位置更加提前。

3 结 论

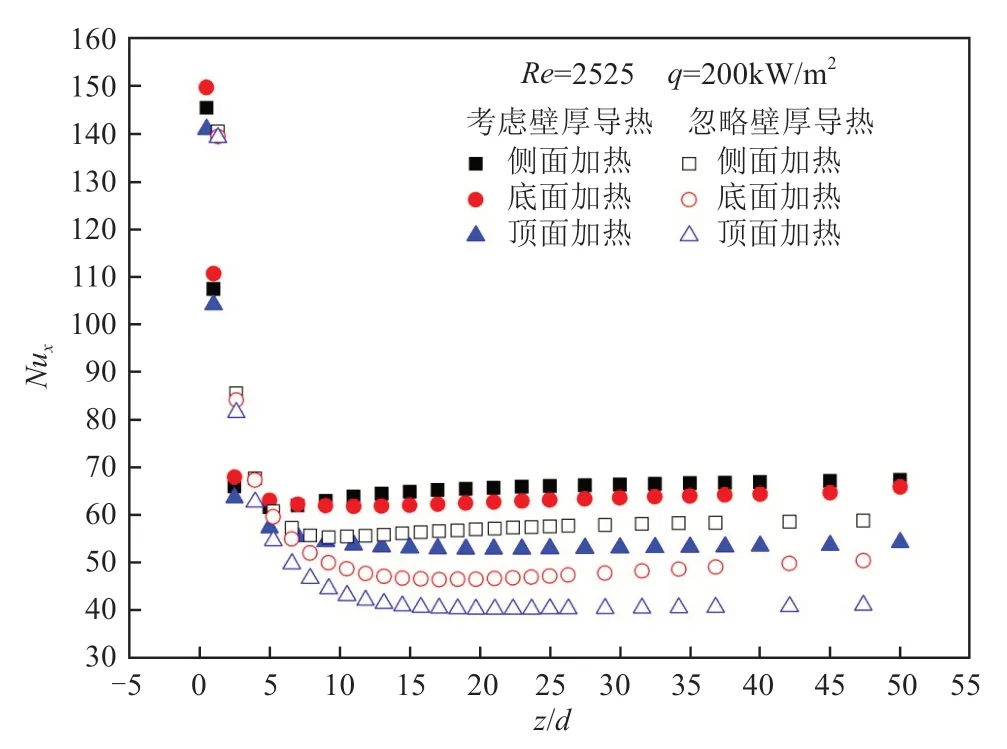
图15 壁面导热对局部Nux随无量纲量y/d变化趋势的影响（Re2525）Fig.15 Influence of tube wall heat conduction on local Nusselt number（Re2525）

本文研究了考虑壁面导热影响的水平方管内的熔盐混合对流传热过程。基于数值模拟方法对单面加热情况下熔盐混合对流的流动特性和传热特性进行了计算与分析，得到了考虑壁面导热影响下熔盐单面加热情况下混合对流传热特性，进一步讨论无量纲参数间的变化关系，并将结果与流型判定图和经典关联式进行对比，可得出如下结论：混合对流传热中存在的浮生力使核心区形状发生改变，核心区与加热面贴近。考虑管壁导热，主流核心区形状更加均匀，局部Nux更高且回升位置更加提前，Nu数随Re数、Ri数的增大而增大，局部Nux数随流动距离的深入先减小后增大。基于混合对流判定准则验证得到数值模拟结果位于湍流混合对流区