一道八上期中压轴题的探究与反思
2019-07-17江苏省兴化市板桥初级中学邹连成
江苏省兴化市板桥初级中学 邹连成
一、题目
已知△ABC 中,边AB=AC=17,BC=16。
(1)△ABC的面积为__________;
(2)已知点E是BC的中点,以AB为斜边在△ABC外构造Rt△ ABD。
①如图1,求线段DE长度的最大值;
②如图2,当AD=BD时,求∠BED的度数。

图1

图2
对于第一问,大部分学生是比较容易解决的,而对于第二问的长度最值问题、度数问题,难度有所上升,对于考生的能力要求也更高。
解:(1)连接AE,利用等腰三角形和勾股定理的知识,可以顺利求出AE=15,则S△ABC=120。
下面先展示参考答案关于问题(2)的全部解答过程。
(2)①如图3,取AB中点F,连接AE、DF、EF。∵AB=AC,BE=CE, ∴ AE⊥ BC, ∴ ∠AEB=∠ADB=90°, ∵AB=17,∴AF=EF=AB=8.5,∵DE≤DF+EF=17,∴线段DE长度的最大值为17。

图3

图4
②如图4,取AB中点F,连接AE、DF、EF,同①可知DF=EF=AF,∴∠FAE=∠FEA。设∠FAE=∠FEA=α,则∠BFE=∠FAE+∠FEA=2α,∵AD=BD,∴DF⊥AB,∴∠BFD=90°,∴∠DFE=90°∴∠AED=∠FED+∠FEA=45°,∴∠BED=∠AEB-∠AED=45°。
二、解法探究
学生在第二问的解答过程中,由直角三角形中斜边的中线等于斜边的一半,可以自然联想到取边的中点,然后连接AE、DE、EF,快速求出DF=EF=AB=,难点在于如何利用长求出最大值呢?学生在此处“卡住”,那怎么解决这个问题呢?笔者进行了如下的探究。
我们可以将这三条线段抽象出来,如图5,那么问题就化简成DF、EF两条固定长度的线段绕点旋转,则≤DE≤DF+EF,则DE≤,则DE≤17,所以DE最长为17。

图5
对于最后一问,笔者从以下几个方面入手去解决这个问题。
解法一:仍然采用第二小问的辅助线连接方式,然后用代数方法去解决几何问题。
如图6,直接设∠DEB=x,∠DEF=y,因为DF=BF=EF,所以∠FBE=∠FEB=x+y,∠FDE=∠FED=y,因为AD=BD,所以∠DFB=90°,又因为∠DOF=∠BOE,所以x+y+x=y+90°,所以x=45°。
解法二:由图可以猜想出DE是∠AEB的角平分线,那么如果能证明这个猜想是正确的,即可把∠BED的度数算出来。
如图7,连接AE,过点D作DF⊥AE于F、DG⊥GC交CB的延长线于点G,因为AD=BD,∠ADB=90°易证△ADF≌△BDG,所以DF=DG=GE,所以∠DEB=45°。

图6
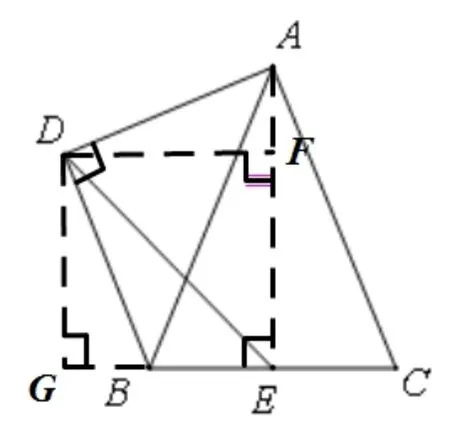
图7

图8
解法三:由等腰直角三角形,可以顺利联想到“一线三直角”。
如图8,因为AD=BD,∠ADB=90°易证△AFD≌△DGB,所以AF=DG=GE,所以∠DEB=45°。
解法四:在研究一些复杂几何问题时,我们经常把图形旋转后再研究,最常见的就是“遇等腰则旋转”。
如图9,将△BDE绕点D逆时针旋转90°得△ADE'。因为∠ADB=∠AEB=90°,所以∠DBE=180°-∠DAE,所以∠DAE'+∠DAE=180°,所以E'、A、E三点共线,又因为DE'=DE,∠E'DE=90°,所以∠DE'E=∠DEB=45°。
或者可以将△ADE绕点D顺时针旋转90°得△BDE',如图10,证明方法同上。
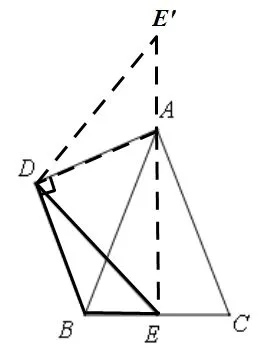
图9

图10
三、教学反思
1.引导学生敢于动手画图,培养探索精神
几何数学的学习一定是在动手操作中发展起来的,学生面对比较复杂的几何问题时,第一反应往往是图形太复杂了,肯定做不起来。这首先是个信心问题,教师在日常教学工作中,要多鼓励学生动手去画,去勇敢尝试。学生自己可以画出来的图形,教师绝不包办,画不出来的图形,尤其是辅助线的画法,教师可以步步引导,讲明、讲透作法的原因,并且给学生最正确的示范作法,防止学生出现作法不规范的情况。总而言之,几何问题一定要让学生敢于动手画图,不要怕失败,只要坚持,一定会有成功的一天。
说到辅助线的画法教学,就拿本题作简要的分析。这里面的三个小问题,并不是单独的,它们其实是层层递进,步步暗示的。第一问的面积问题,就暗示了必须要把AE连接起来,解决第二问时,就很容易看到两个直角三角形共有一条斜边,进而就提醒了考生,要取斜边中线。紧接着,第三问又承接第二问的辅助线的作法,利用代数方法很快就解决了这个问题。其实这些“线索”,学生通过现场动手画图完全是可以想出来的,所以教师在平时教学中,要时常渗透这一思想,当学生在做题过程中能自然地想到这些,那么我想他的数学思维就形成了。
2.加强数学几何模型教学,形成数学直觉
几何问题的解决一直是初中教学的一大难点,主要是因为几何定义、性质多且杂,学生记忆起来就很困难了,运用这些知识去解决问题就更难了。笔者认为,在日常教学中,可以多向学生介绍一些常见的几何模型,比如“八字形”“K型图”“筝型图”等。教师在介绍这些几何模型的过程中,灵活地将众多几何知识有机结合在一起,并用这些模型去解决问题,这样学生在感受的过程中,就把零散的几何概念整合了起来,运用起来也能更得心应手。当学生可以自觉地将几何知识统一运用的时候,那么几何学习就彻底活起来了。此外,几何模型的教学不仅可以帮助学生整合知识,更可以增强学生对几何学习的兴趣,甚至有的学生会下意识地模仿教师介绍的几何模型,去创造适合自己的专属模型。相比较照本宣科的单纯的概念教学,海量的题目覆盖,切切实实,认真准备一些专题几何模型教学课,我想可以真切地帮助学生减轻学习的思维压力。换种角度看,这也是一种减负。
