基于NSST和稀疏表示相结合的图像融合算法
2019-07-16杜进楷丁冬冬龙海莲陈世国
杜进楷 丁冬冬 龙海莲 陈世国


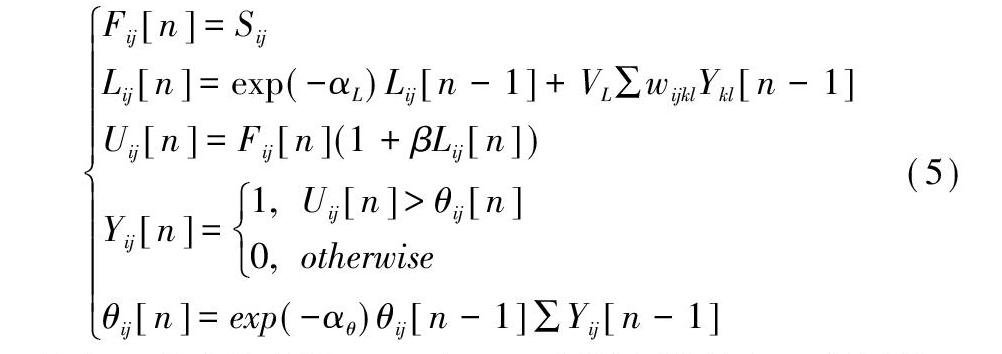
摘要:本文针对传统的多尺度变换和稀疏表示在图像融合中存在的一些不足,提出了一种基于非下采样shearlet变换(NSST)的低频域稀疏表示(SR)和高频域脉冲耦合神经网络(PCNN)的图像融合算法(简称NSST-LSR-HPCNN),并对低频域稀疏表示系数采用改进的拉普拉斯能量和(SML)取大的规则进行融合。仿真结果表明,NSST-LSR-HPCNN算法中低频域稀疏表示系数采用SML取大的规则融合图像的空间频率SF、互信息量MI、边缘保持度QAB/F的数值均高于本文其他几种对比算法融合图像的数值,在高频域融合规则相同的情况下,相比于低频域稀疏表示系数采用L1范数取大的融合规则,本文算法的SF提高了0.19%、MI提高了5.98%、QAB/F提高了0.57%,SF、MI、QAB/F指标均具有较优值。本文算法有效的综合了红外图像和可见光图像中的信息,融合图像更加全面的携带了源图像中的有效信息特征,在主观视觉效果和客观评价指标上均优于其他几种对比融合算法。
关键词:多尺度变换;稀疏表示;低频域;高频域;红外图像;可见光图像
中图分类号: TP302 文献标识码:A
文章编号:1009-3044(2019)15-0217-06
Abstract: Aiming at some shortcomings of traditional multi-scale transform and sparse representation in image fusion, this paper proposes a low-frequency domain sparse representation (SR) and high-frequency domain pulse coupled neural network (PCNN) based on non-subsampled shearlet transform (NSST). Image fusion algorithm (NSST-LSR-HPCNN for short), and the low-frequency domain sparse representation coefficient is fused by the improved Laplacian energy and (SML) large rules. The experimental results show that the spatial frequency SF, mutual information MI and edge retention QAB/F of the NSST-LSR-HPCNN algorithm in the low-frequency domain sparse representation coefficient using SML are larger than the other comparisons. The value of the algorithm fusion image, when the high-frequency domain fusion rule is the same, compared with the low-frequency domain sparse representation coefficient using the L1 norm to enlarge the fusion rule, the SF of the algorithm is increased by 0.19% and the MI is increased by 5.98%. QAB/F increased by 0.57%, and the SF, MI, and QAB/F indicators all had superior values. The algorithm effectively combines the information in the infrared image and the visible light image. The fused image carries the effective information features in the source image more comprehensively, and is superior to other comparison fusion algorithms in subjective visual effects and objective evaluation indicators.
Key words: multiscale transformation; sparse representation; low frequency domain; high frequency domain; infrared image;visible image
圖像融合是指将多个图像传感器或同一图像传感器以不同的工作模式获取的关于同一场景的图像信息加以综合,以获得新的关于此场景更加准确的描述[1]。在实际应用中,多个图像传感器或同一图像传感器模式设置的不同所获得的图像信息具有一定的冗余性和互补性,通过图像融合技术,将所得的图像进行融合处理,可以进一步提高图像的清晰度,使得图像的信息量增加。在同一场景下,红外图像可以反映出目标的红外热辐射能量分布,具有较强的对比度,受外界环境影响较小,但不能很好地表现目标及场景的细节信息;可见光图像可以很好地表现出目标及场景的细节信息,但易被外界环境所干扰。通过图像融合技术,将红外和可见光图像进行融合,达到一种优势互补,使得图像既具有较强的对比度,又能很好地表现出目标及场景的细节信息和对环境的适应能力。因此,红外与可见光图像融合是十分有意义的,已被广泛应用于图像去雾、安全监控和军事侦察等领域[2]。
在变换域图像融合方法中,基于多分辨率分析的图像融合方法目前受国内外图像融合研究者关注较多,应用也较为广泛。多分辨率分析方法中,小波变换的时频局部化特性较为良好,在图像融合领域得到了广泛的应用。由于小波变换不具有平移不变性,并且捕获到的方向信息较为有限,会导致融合图像的细节信息丢失[3],针对这一局限性,Minh N Do等人提出了Contourlet变换[3]。Contourlet变换不仅具有小波变换的优点,还具有各向异性,但不具有平移不变性,会导致图像奇异点周围的伪吉布斯现象[4]。针对这一不足,Cunha A.L等人提出了非下采样Contourlet变换(NSCT) [5],但 NSCT 模型的计算复杂度较高,运行时间过长,处理效率较低。Shearlet变换[6-7]是Demetrio Labate等人在2005年提出的一种新的多尺度变换,相比于Contourlet变换和NSCT,Shearlet变换不会限制支撑基的尺寸和分解的方向数,而且其逆变换不需要对方向滤波器进行逆合成,只需要对正向变换中的Shearlet滤波器进行加和处理,从而使得实现效率较高[8]。由于Shearlet变换不具有平移不变性,还会导致图像奇异点周围的伪吉布斯现象,K.Guo和G.Easley等人提出了非下采样Shearlet变换 (NSST)[9],可以克服这一不足,不仅保持了NSCT的一些优良特性,而且具有更高的效率。将其应用在图像融合中,可以显著地提高融合图像的质量,并且提高融合的效率。
本文的研究工作主要是基于NSST和稀疏表示、PCNN几种算法相结合进行红外和可见光图像的融合。对源图像进行NSST分解后,会得到不同尺度的低频分量和高频分量,而各个分量融合规则的选择对融合图像的质量起着至关重要的作用。NSST分解的低频分量稀疏性较差,采用稀疏表示的融合方法,对其使用K-SVD算法进行字典训练并对去均值后的图像块分别采用OMP算法计算稀疏表示系数,然后对稀疏表示系数采用SML取大的融合规则进行融合。NSST分解的高频分量描述了源图像的细节信息,传统的加权平均、绝对值取大等方法用于高频分量的融合,会导致图像细节的丢失,不能取得较为理想的融合效果。脉冲耦合神经网络(PCNN)具有位移、旋转、尺度和扭曲不变的特性,而且可以贯穿整幅图像的自动波[10-11],将其应用到图像融合中,可以保留源图像的更多细节信息,取得较好的融合效果。最后使用NSST逆变换重构融合的低频分量和高频分量得到融合图像。通过在MATLAB环境下进行仿真,结果表明,本文提出的算法融合的图像可以进一步提高图像的清晰度、增加图像的信息量,融合效果较为理想。
1 非下采样Shearlet变换
Shearlet变换[6-7]是Demetrio Labate等人在2005年提出的一种新的多尺度变换,克服了 Contourlet 变换和NSCT在支撑基的尺寸和分解方向数上的限制,并且提高了运算效率。 当维数n=2时,具有合成膨胀的仿射系统定义如式(1)所示
式中:[f∈L2(R2)],则[AAS(ψ)]中的元素称为合成小波。A称为各向异性膨胀矩阵,[Aj]与尺度变换有关,S为剪切矩阵,[Sl]与保持面积不变的几何变换有关。特别地,当A=[4 0 0 2],S=[1 1 0 1]时,此时的合成小波为剪切波。NSST[12]是K.Guo和G.Easley等人2008年在shearlet变换的基础上提出来的一种非正交变换,其离散过程主要包括基于非下采样金字塔滤波器组的多尺度分解和基于改进的剪切波滤波器组的多方向分解两部分[13],其分解原理如图1所示。这一模型可以避免下采样的操作,从而具有平移不变性,使得分解的图像具有较高的冗余度,用于图像融合中,可以取得较好的融合效果。
2 稀疏表示理论模型
稀疏表示[14]是Olshausen和Field在1996年提出的,他们认为每幅图像都可以看成多个基函数的线性组合,这些基函数可以经过多幅图像的训练估计出来[13]。其数学模型如式(3)所示:
上述方程的求解常用的方法有基追踪(BP)算法、匹配追踪(MP)算法、正交匹配追踪(OMP)算法等,其中,OMP算法克服了BP算法复杂度高和MP算法原子之间不正交的问题,具有较高的计算效率,而且能达到最优收敛[15]。因此,本文选择OMP算法来计算图像低频分量的稀疏系数。
从上述模型中可以看出,过完备字典D的选取对图像处理的效果起着至关重要的作用,本文选择文献[16]中所采用的K-SVD[17]方法來训练字典,其数学优化目标函数如式(4)所示:
3 PCNN的简化模型
脉冲耦合神经网络(PCNN)是根据猫的视觉皮层上的神经元同步脉冲发放现象提出的神经元模型,是一种不同于传统人工神经网络的新型神经网络,成功应用在图像处理的一些领域[18]。
PCNN 神经元模型是反馈型神经网络的一种模型,由若干个PCNN神经元互相连接构成的,其中的每一个神经元都由三部分组成,分别是:接受域、调制部分、脉冲产生器[19]。传统的PCNN模型所设置的参数较多,运行过程较为复杂,本文采用如图2所示的简化模型,使得神经元的输入通道F只接受外界刺激,链接通道L接受周围神经元的输出,其数学方程描述如式(5)所示。
式中,n为迭代次数,Fij[n]和Lij[n]分别为像素点(i,j)位置第n次迭代时的输入项和链接项,Sij为外界刺激,本文选择高频域每一像素点处的灰度值作为外界刺激,αL和VL分别表示链接域中衰减时间常数和放大系数,Wijkl表示链接域的连接权值系数,Uij[n]为像素点(i,j)位置第n次迭代时的内部活动项,β为神经元的链接强度,Yij[n]为像素点(i,j)位置第n次迭代时的输出时序脉冲序列,θij[n]为像素点(i,j)位置第n次迭代时的动态门限阈值,αθ和Vθ分别表示动态门限的衰减时间系数和放大系数。
PCNN的简化模型工作过程为:接受域接受来自外部的刺激和相邻神经元的输出,通过F通道和L通道传送到内部活动项中。调制部分利用相邻神经元的耦合链接,将L通道的信号加上一个正的偏移量β后与L通道的信号进行相乘调制,可以得到神经元的内部活动信号[Uij] 。接着传递[Uij]到脉冲产生部分,并与动态门限阈值
4 图像融合算法
4.1 NSST分解图像
使用NSST分别对配准好的待融合的红外和可见光源图像进行分解,分解的尺度为4,剪切方向数设为[3,3,4,4],滤波器选择“maxflat”滤波器。然后对分解后的低频分量和高频分量根据各自的特征分别采用合适的融合算法进行融合处理。
4.2 低频分量的融合
对低频分量融合规则的选择决定了融合图像对源图像大部分信息的保留程度。本文基于低频分量稀疏性较差这一局限性,采用了稀疏表示的融合算法,当前大部分文献对稀疏表示系数选用绝对值取大的融合规则,这一方法只是考虑了单个像素的特性,没有考虑到系数间的相关性。本文采用SML这一典型清晰度评价融合性能的指标用于稀疏系数的融合,对低频域的稀疏表示系数采用SML取大的规则进行融合。
融合步骤如下:
(1) 利用步长为s像素的滑动窗口把NSST分解的低频分量从左上到右下依次划分为[n×n] 大小的图像块,将采集到的图像块分别记为[piATi=1]和[piBTi=1],其中,T为图像块的总数,本文采用的滑窗大小为8×8,步长为1。
(5) 对[piATi=1]和[piBTi=1]的所有图像块执行上述(2)—(4)的操作,可以得到所有图像块的融合结果[viFTi=1]。对每一个块向量[viF],将其转换为[] 的图像块形式[piF],放到低频空间坐标系的对应位置,再对重复像素取平均后可得到最终的低频结果LF。
4.3 高频分量的融合
对高频分量融合规则的选择决定了融合图像对两幅源图像中细节的保留程度。本文基于高频分量的这一特性,采用了PCNN的融合算法。
首先,对待融合图像的高频分量分别进行归一化操作,将其每一像素(
4.4 NSST逆变换重构图像
使用NSST的逆变换对融合后的低频分量和高频分量进行重构,从而得到融合图像。
5 实验结果及分析
5.1 实验图像选取
为了对本文所提出算法的效果进行验证,选取了两幅256×256大小的红外和可见光源图像进行融合仿真实验。如图3为本文选取的进行仿真实验的红外图像,如图4为本文选取的进行仿真实验的可见光图像。
5.2 实验图像融合
为了验证本文所提出算法的性能,实验中将融合领域中的一些算法与本文算法进行比较。算法一为基于离散小波变换的图像融合算法得到的融合图像,使用离散小波变换对配准好的待融合的红外和可见光源图像进行分解,分解层数为4层,小波基函数选择“db4”,低、高频分量的融合规则与本文所用的融合规则相同,如图5为算法一得到融合图像。算法二为基于NSCT的图像融合算法得到的融合图像,使用NSCT对配准好的待融合的红外和可见光源图像进行分解,使用‘9-7滤波器作为塔型分解滤波器,使用‘pkva滤波器作为方向滤波器,四个分解层的方向数量依次为3、3、4、4,低、高频分量的融合规则与本文所用的融合规则相同,如图6为算法二得到的融合图像。算法三为基于NSST的图像融合算法得到的融合图像,使用NSST对配准好的待融合的红外和可见光源图像进行分解,NSST的参数设置与本文算法中NSST的参数设置一样,分解后的低频分量选择加权平均的方法进行融合处理,高频分量选择绝对值取大的方法进行融合处理,如图7为算法三得到的融合图像。算法四为基于NSST的图像融合算法得到的融合图像,使用NSST对配准好的待融合的红外和可见光源图像进行分解,NSST的参数设置与本文算法中NSST的参数设置一样,分解后的低频分量选择稀疏表示的方法,并选择稀疏表示系数绝对值取大的融合规则选择稀疏表示系数,高频分量选择PCNN的方法进行融合处理,PCNN模型的参数与本文所用的算法中PCNN参数一样,如图8为算法四得到的融合图像。算法五为基于NSST的图像融合算法得到的融合图像,使用NSST对配准好的待融合的红外和可见光源图像进行分解,NSST的参数设置与本文NSST的参数设置一样,分解后的低频分量选择稀疏表示的方法进行融合处理,并选择空间频率取大的融合规则选择稀疏表示系数,高频分量选择PCNN的方法进行融合处理,PCNN模型的参数与本文所用的算法中PCNN参数一样,如图9为算法五得到的融合图像。如图10为本文算法得到的融合图像。
5.3 实验结果分析
为了客观地评价图像的融合效果,本文选择空间频率(SF)这一基于梯度值的评价指标和互信息量(MI)、边缘保持度QAB/F两种基于源图像的评价指标对融合仿真结果进行评价分析。SF可以反映出空间域内图像的总体活跃程度,MI计算源图像有多少信息转移到了融合结果中,而QAB/F利用Sobel边缘检测来衡量有多少边缘信息从源图像转移到融合图像[20],三者的值越大,说明所采用的算法的融合性能越好。如表1为各种融合算法所得的融合图像评价指标比较,从给出的6种融合算法的各项评价指标可以看出,采用同样的融合规则,NSST分解方法融合图像的SF、MI和QAB/F均高于DWT和NSCT分解方法融合圖像。NSST分解方法中,高频域采用同的融合规则,低频域使用稀疏表示的方法中,对稀疏表示系数采用基于SML取大的融合规则融合图像的SF、MI和QAB/F的数值均高于采用稀疏系数绝对值取大和采用基于SF取大的融合规则融合图像的数值,并且本文所提出的算法融合图像的SF、MI和QAB/F的数值高于传统的基于NSST分解的低频域加权平均高频域绝对值取大的融合图像的数值。综合主观评价和客观评价的各项指标可以看出,图10的融合效果较为理想。
6 结论
本文以NSST为基本框架进行红外和可见光图像融合,将稀疏表示方法用于低频分量的融合,将PCNN的方法用于高频分量的融合,并对低频域稀疏表示系数采用改进的拉普拉斯能量和(SML)取大的规则进行融合。与其他方法的对比实验结果表明,本文提出的算法在主观视觉效果的定性评价和客观融合信息定量评价两方面均优于其他几种算法。
参考文献:
[1] 苗启广,叶传奇,汤磊,李伟生.多传感器图像融合技术及应用[M].西安.西安电子科技大学出版社,2014.
[2] 李博博,马泳,张晓晔,樊凡.基于BMA滤波器和边缘的红外与可见光图像融合[J].红外技术,2018,40(2):139-145.
[3] Do M N, Vetterli M.The contourlet transform: an efficient directional multiresolution image representation[J]. IEEE Transactions on Image Processing, 2005, 14(12): 2091-2106.
[4] Qu Xiao-Bo,YAN Jing-Wen,XIAO Hong-Zhi,ZHU Zi-Qian. Image Fusion Algorithm Based on Spatial Frequency-Motivated Pulse Coupled Neural Networks in Nonsubsampled Contourlet Transform Domain[J]. Acta Automatica Sinica,Vol.34,No.12, pp: 1508-1514.Dec.2008.
[5] Da Cunha A L, Zhou J P, Do M N.The nonsubsampled contourlet transform: theory, design, and applications.IEEE Transactions on Image Processing, 2006, 15(10): 3089-3101.
[6] D.Labate, W.Q.Lim, G.Kutyniok, et al. Sparse multidimensional representation using Shearlets[C]. Optics&Photonics 2005. San Diego: International Society for Optics and Photonics, 2005, 59140U-59140U-9.
[7] Easley G, Labate D, Lim W Q. Sparse directional image representations using the discrete shearlet transform [J]. Applied & Computational Harmonic Analysis, 2008,25(1):25-46
[8] 杨勇,万伟国,黄淑英,姚丽.稀疏表示和非下采样Shearlet变换相结合的多聚焦图像融合[J].小型微型计算机系统,2017,38(2): 386-392.
[9] G.Guorong,X.Luping,and F.Dongzhu,“Multi-focus image fusion based on non-subsampled shearlet transform”,IET Image Process, Vol.7,No.6,pp:633–639,2013.
[10] K.Zhan,J.Shi,H.Wang,Y.Xie,Q.Li. Computational Mechanisms of Pulse-Coupled Neural Networks:A Comprehensive Review[J]. Archives of Computational Methods in Engineering.Vol.24,No.3,pp:573–588.July.2017.
[11] J.Zhang,K.Zhan,and Y.Ma. Rotation and scale invariant antinoise PCNN features for content-based image retrieval[J].Neural Network World.Vol.17,No.2,pp:121–132.20
[12] Easley G, Labate D, Lim W Q. Sparse directional image representations using the discrete shearlet transform[J]. Applied computational harmonic analysis, 2008, 25(1): 25-46.
[13] 王志社,杨风暴,彭智浩.基于NSST和稀疏表示的多源异类图像融合方法[J].红外技术,2015,37(3):210-217.
[14] B.A.Olshausen, D.J.Field. Emergence of simple-cell receptive field properties by learning a sparse code for natural images[J]. Nature,1996,381 (6583): 607-609.
[15] 刘战文,冯燕,李旭,丁鹏飞,徐继明.一种基于NSST和字典學习的红外和可见光图像融合算法[J].西北工业大学学报,2017,35(3):408-413.
[16] Yu Liu, Shuping Liu and Zengfu Wang, "A General Framework for Image Fusion Based on Multi-scale Transform and Sparse Representation", Information Fusion, vol. 24, no. 1, pp. 147-164, 2015.
[17] Aharon M, Elad M, Bruckstein A. K-SVD: an algorithm for designing over complete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.
[18] T.Lindblad J.M.Kinser.脉冲耦合神经网络图像处理[M]. 马义德,绽琨,王兆滨,等.译.北京.高等教育出版社,2008.
[19] Ming Yin, Xiaoning Liu, Yu Liu*, Xun Chen.Medical Image Fusion With Parameter-Adaptive Pulse Coupled Neural Network in Nonsubsampled Shearlet Transform Domain[J]. IEEE Transactions on Instrumentation and Measurement, in press, 2018.
[20] QU Xiao-bo,YAN Jing-wen,YANG Gui-de.Sum-modified-Laplacian-based Multifocus Image Fusion Method in Sharp Frequency Localized Contourlet Transform Domain[J].Optics and Precision Engineering, 17(5): 1203-1202, June 2009.
【通联编辑:梁书】
