浅谈平均指标的科学运用

□郭子君

一、引言

平均指标是同类社会和经济现象总体在一定时期内各单位特征值一般水平的统计指标，是抵消整个社会经济现象中个体特征值差异的结果，是一个代表性数值，体现了整个总体的数量特征。平均指标是统计描述分析中的重要部分，广泛应用于社会经济统计学。例如，通过比较同期中国的城镇居民人均可支配收入和农村居民人均收入，可以反映出中国城乡居民收入间的差异；通过观察劳动生产率和职工平均工资可以发现这二者之间的依存关系，劳动生产率提升，职工的平均工资也会相应提高。平均指标的主要类型有数值型平均值和位置平均值，算术平均数、调和平均数、几何平均数为数值平均值，中位数、众数为位置平均值。算术平均值是最常用的平均指标。由于平均指标形式众多，在使用过程中就容易出现问题，如果使用不当，不仅不能客观反映现实情况，还会产生误导，影响人们对实际的认识和判断。国家统计局公布2018年城镇非民营单位年均工资为82461元，比上年增长11.0%，数据公布之后，引起强烈反响，众多新闻媒体用“你拖后腿了吗？”“你达标了吗？”等标题表达了与实际不符的质疑，广大职工认为这个数据过高，这一现实表明，用城市非民营单位的就业人员年平均工资反映全国城市就业人员的工资收入水平有些不合适。

二、各类平均指标的缺陷

（一）算数平均数

算术平均数并不是总能够代表整体的一般水平。

例，有A、B 两组职工生产零件，A 组五名职工生产零件个数分别为：30、64、136、90、20，B组工人生产零件个数分别为：62、64、68、72、74。

A组工人平均生产零件个数为：

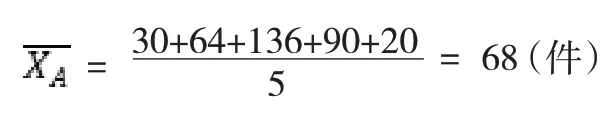
B组工人平均生产零件个数为：

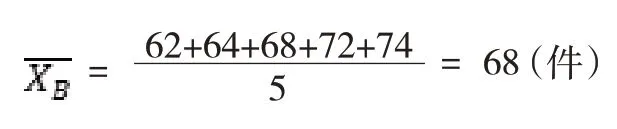
由A、B 两组数据可以看出，相对而言，68 件更能代表B组的生产水平。由此可知，当总体各单位特征值差异较小时，用算术平均值就可以很好的代表整个群体，但是当总体各单位标志值表现不均衡时，继续用算术平均值代表整体就不合理了。调和平均数的形式虽然和算术平均值不同，但是含义是一致的，所以其特点与算术平均值也相同，就不多作解释了。

（二）几何平均值

几何平均值是用于计算平均速度或者平均比率的平均指标。其计算公式为：

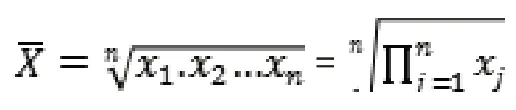
由公式可知：（1）几何平均值的数值受每个变量值的影响，因此可知极端变量值会对几何平均值产生较大影响。（2）当变量值当中有负数时，计算出的几何平均值就变为负值或者是虚数。

可见，当各单位标志值为等比和接近等比的关系时，可以用几何平均数来作为其平均指标。

（三）众数

一组数据中最多出现的变量值称为众数，在次数分布图上，众数是曲线的最高峰所对应的标志值，由此可知众数无需计算，它是一种位置平均值。

众数的定义决定了它不受极端值的影响，但是对于分组数据而言，不同的分组情况会导致出现不同的众数，而且分组数据中没有任何一组的次数比较突出，即当分布数列中没有明显的集中趋势时，则认为没有众数。

（四）中位数

将所有数据按大小顺序排列起来，形成一个数列，而数列最中间位置上的数据就是中位数，因此中位数可以将整体数据进行划分，一半大于中位数，另一半小于中位数。

中位数作为一个位置平均数，它不受到极端值的影响，这一特点在一定程度上提高了其对于整体数列的代表性，但是当整体数据分布偏斜时，其代表性就会降低。

三、应用平均指标遵循的原则

（一）根据数据的特征以及说明对象选择合适的平均指标

要根据所掌握的资料是否为数值型数据，以及数据的特点是否具有均衡性或者有明显的集中趋势而选择合适的平均指标代表总体。例：某公司员工的月薪如表1所示。

从表1中可以看到该组数据分布不均衡，有极端值，因此不宜选择算术平均数代表总体，而是选择中位数或者众数来作为整体的工资水平。

（二）把握现象的同质性原则

社会经济现象总体中各单位被平均的标志属于同类就是具有同质性，之所以可以计算平均指标就是基于同质性。如果总体各单位是不同质的，那就不可能存在一个一般水平，更不可能揭示各单位的共同规律性。如果将若干具有本质差异的现象混合起来计算其平均指标，就会将现象之间的本质差异隐藏，从而歪曲了现象的实际情况。

（三）用分组以后的组平均值对总体平均值进行补充说明

总体平均值是将所有单位混合在一起运算的，它是将各单位之间的差异抽象掉了结果，用来说明各单位的一般水平，但是仅仅依靠总平均值还不能全面说明总体的特征，需要对总体先分组，计算组平均值，以补充说明总平均值。例如，有A、B两个企业工人工资资料如表2所示。

从表2 中的平均工资来看，A 企业为475 元，B 企业为472 元，A 企业的工资水平高于B 企业，但从分组后计算的组平均工资看，不管是工人还是管理人员都是B企业的工资水平高于A 企业，其原因是由于A 企业中工人的比重低于B企业，而工人的工资要比管理人员低，受A、B 两企业员工人数结构差别的影响，使得A 企业总平均工资高于B 企业。由此可见，只用总体平均值说明问题是不充分合理的，必须用组平均值来补充说明总体平均值。

（四）用次数分布数列补充说明总体平均值

为了全面深入地分析问题，我们不仅要看现象的平均水平，还要了解平均水平掩盖下的各单位数值的次数分布情况，把总平均数和次数分布资料结合起来。

例：某集团50个企业年度生产计划的完成情况如表3所示。

由表3 可知，这50 个企业的平均计划完成程度为105%，表现为超额完成计划。但从次数分布数列来看，有18%的企业没有完成计划，此外也有一大批企业超出较多份额完成了原计划，次数分布数列的补充说明令分析整体企业集团的计划执行情况更全面也更深入。

表1 某公司员工月薪表 单位：元

表2 A、B企业员工工资表

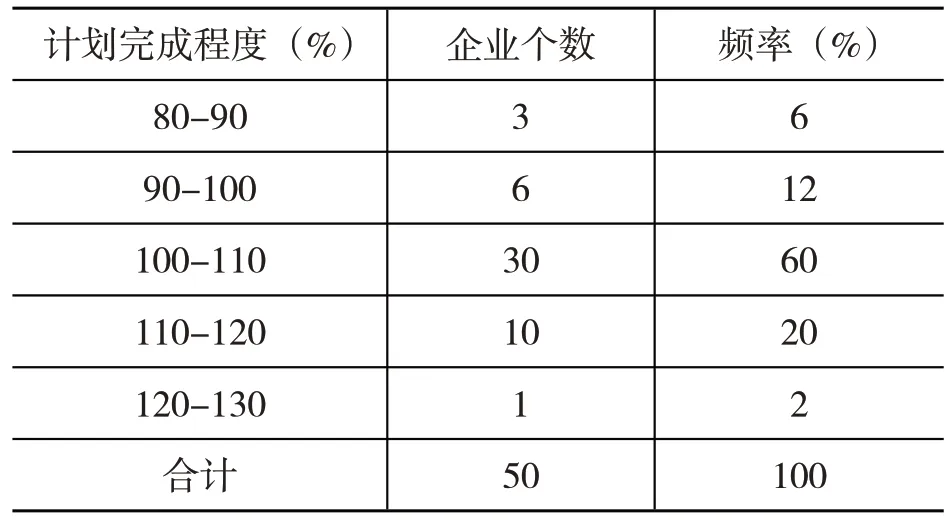
表3 某集团50个企业年度生产计划完成情况

（五）平均指标与变异指标相结合

平均指标是一个重要的统计指标，它表明了总体各单位某一数量标志的一般水平。但是，平均指标将总体各单位标志值的差异抵消化了，作为总体的代表值，它不能反映出个体的差别，而变异指标可以综合反映总体各单位某一特征值的差异程度或离散程度。将二者结合使用，可以对总体有更清晰的认识，有效的进行科学管理和判断。