A Squared-Chebyshev wavelet thresholding based 1D signal compression

Hnn A.R. Akkr , Wel A.H. Hdi , Irheem H. Al-Dosri

a Electronic Engineering in University of Technology, Iraq

b Communication Engineering in University of Technology, Iraq

c Electronic Engineering at Al-Rafidain University College, Iraq

Keywords:PDR (percentage root mean squared difference)RMSE (root mean square error)Signal compressionSquare wavelet thresholding

A B S T R A C T In this paper a square wavelet thresholding method is proposed and evaluated as compared to the other classical wavelet thresholding methods(like soft and hard).The main advantage of this work is to design and implement a new wavelet thresholding method and evaluate it against other classical wavelet thresholding methods and hence search for the optimal wavelet mother function among the wide families with a suitable level of decomposition and followed by a novel thresholding method among the existing methods. This optimized method will be used to shrink the wavelet coefficients and yield an adequate compressed pressure signal prior to transmit it. While a comparison evaluation analysis is established, A new proposed procedure is used to compress a synthetic signal and obtain the optimal results through minimization the signal memory size and its transmission bandwidth.There are different performance indices to establish the comparison and evaluation process for signal compression; but the most well-known measuring scores are: NMSE, ESNR, and PDR. The obtained results showed the dominant of the square wavelet thresholding method against other methods using different measuring scores and hence the conclusion by the way for adopting this proposed novel wavelet thresholding method for 1D signal compression in future researches.

1. Introduction

In mathematics, wavelets are considered as another way to construct the signal model based on some special signals known as wavelets, which are short in time extent and alternator oscillating with certain amplitude. Wavelets have asymmetric and irregular bases unlike Fourier series which has smooth sinusoid bases [1].

Most of the signals in real life have sharp changes, and these discontinuities are better analyzed with irregular wavelets than smooth sinusoids,just like some food which can be better handled with a fork than a spoon [2]. Wavelet transform is a good tool for signal analysis and one of its applications is the denoising and compression for signals and images. In this work a special type of signal is adopted which is synthesis signal created by an internal pressure measuring process inside a pipeline [3].

In any measurement process for a physical parameter a sensing element is required,which is used to convert the required signal to a suitable form which can be read by the next stage. However this process unfortunately cannot be done safely without an existence of an inherent noise which will disturb the original data [4].

Thus;the appropriate suggestion for any measuring process is a signal compression; in order to get a precise measurement at the final process,and signal compression can be achieved via different algorithms such as wiener filtering,wavelet transform and spectral subtraction [5].

Wavelet transform based signal compression can be summarized by three steps [6]:

(1) Transform the signal from time domain to the wavelet domain such that most of the signal energy concentrated in few wavelet coefficients know as approximation.

(2) Thresholding the detail wavelet coefficients which are considered as a non-required part of the signal(i.e.inherent noise).

(3) Re-transform back the wavelet coefficients (approximation and details) from wavelet domain to the time domain and hence get the compressed signal.

The contribution to the knowledge in this work is a proposed square wavelet thresholding method which can be considered as a modification for the well-known thresholding method (soft and hard), in such a manner which is analogy to the contrast between Butterworth and Chebyshev filter characteristics.

It is clear that; in Butterworth filter the pass band is flat and ripples free in contrast to the Chebyshev filter which has ripple in the pass band.This idea is developed for the wavelet thresholding function to compare the ordinary soft and hard thresholding which are ripple free with the new proposed thresholding methods which have ripples in the pass band making them like Chebyshev filter characteristics[7].

The proposed ripples can take a form of tiny squared signal rather than sinusoids just like a barber which has different combs for different hairdressing and usages.

2. Recent wavelet thresholding methods

One of the most interesting points for the researcher in the wavelet thresholding domain is how to improve the thresholding method or the threshold selection rule in order to get an optimal results that minimize certain criteria such as MSE (mean square error), RMSE (root mean square error), NMSE (normalized mean square error), PDR (percentage root mean square difference), or maximizing other performance indices such as PSNR(peak signal to noise ration), and ESNR (enhancement signal to noise ratio)[8].

So the last years related work in the developing the thresholding methods can be summarized by:

(1) wavelet thresholding function was proposed by Xiaobin Xu as a modification for the soft and hard thresholding by augmenting two factors [shaping and scaling] to make it continuously differentiable at all points, and give it maximum adaptability with the input signal under compression process [10].

(2) Another work of Zhang Jianhua1 in suggesting a new hierarchy for thresholding method that overcome the problem of global threshold by choosing self-adaptive thresholds based on the fact of noise decay rate in the wavelet detail coefficient [9].

(3) On the other hand; wavelet transform based logarithmic thresholding is used by Hayat Ullah for compression of images, corrupted by noise (during under-sampling in the frequency domain) [11].

The logarithmic shrinkage technique is applied to undersampled Shepp-Logan Phantom image. the experimental results shows 10%enhancement over the traditional thresholding methods in removing different type of noise such as salt and pepper,Gaussian, speckle, and Poisson noises. In addition to that, the experiments shows 35% enhancement over the classical methods if wiener filtering with median threshold is combined with the logarithmic wavelet thresholding method [12].

(4) an additional work done by Koteswararao which propose a wavelet based estimation to de-noise 1D or 2D signal by evaluating threshold value using FDR,Visu and Top rules.The proposed algorithm was implemented and simulated using MATLAB with the performance indices such as Signal to Noise Ratio (SNR) and Mean Square Error (MSE) [13]. From the work analysis, it was observed that the mixed function performs better than all existing functions for 1D and 2D signals in FDR and Visu rules while, in top rule, the mixed function performs better only in hard thresholding for both 1D and 2D signals [14].

(5) In 2018;Hui Liu proposed a new wavelet thresholding based on noise variance estimation which is known as improved thresholding function.the study puts forward the strategy of using two-state Gaussian mixture model in order to classify the high-frequency wavelet coefficients in the minimum scale accordingly, the experiment with different test signals shows the suitability of the improved thresholding for electro-mechanical transmission system because it combines the advantages of the soft and hard thresholding methods[15]. Our proposal of wavelet thresholding method is to augment the soft and hard thresholding by square signal as a ripple in their pass -band region such that a new softysquare and hardy-square thresholding methods are constructed which can be shown in Fig.1.

3. Process measuring scores

There are different performance measures to evaluate the compression process, and these measures depend in their evaluation for compression calculations on the original clean signal and the compressed signal characteristics,Table 1 shows some of these performance measure which is used in the work to evaluate the proposed thresholding method and compare it with the classical methods. Also the correlation between the basis and the analyzed signal is an important measure for the success of the analysis process since as high as the cross correlation between the scaling wavelet function with the signal to be analyzed yields the most cumulative energy concentrated in few number of wavelet approximation coefficients,leaving the details wavelet coefficients represent the unwanted noise, which will be shrinkage in the further compression steps after signal decomposition [16]. The results of correlation between the noisy synthesis pressure signal with different family of wavelet scaling function are shown in Table 2.

4. System mathematical equation

Wavelet thresholding represent the backbone for the wavelet compression algorithm and the research area for developing the thresholding techniques still has a good area in the researcher thinking, while the first thresholding method was supposed at 1995 by Donoho[17].The researchers nowadays still developed the thresholding method,for example at 2018 augmented,logarithmic,mixed,and improved thresholding methods are suggested for both signal and image compression.

Fig.1. Proposed hardy-square and softy-square.

Table 1Different performance indices for evaluation of signal compression algorithm.

Table 2Cross correlation between the noisy pressure signal and wavelet scaling

The mathematical equation for the thresholding function which represent the input-output characteristics for this process is described by

(1) Softy-square thresholding

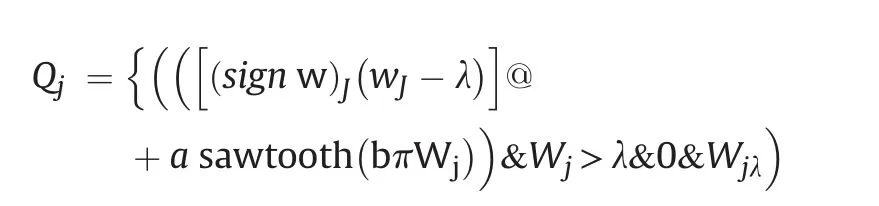
(2) Hardy-square thresholding

(3) Hard thresholding

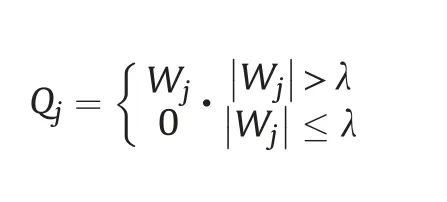
(4) Soft thresholding

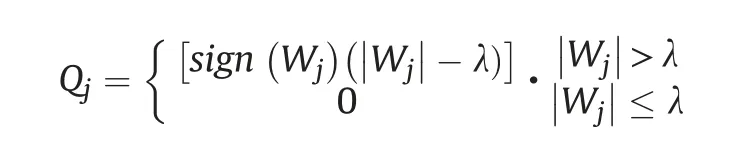
5. Results and discussion

A synthesis pressure signal with 100 sample is constructed which simulate a pressure inside an pipeline with an estimated leak of size 0.25′′,in addition to that a simulated random noise signal is added to the clean pressure signal such that a noisy pressure signal is constructed which will be the input to the compression algorithm. The proposed wavelet thresholding method was simulated and tested using matlab 2017.

Among different wavelet families,and based on the correlation between wavelet mother function and the signal under test,symlet family is selected to evaluate the proposed thresholding method and the results of comparison with the classical soft and hard thresholding methods are explained in details in Tables 3-5.

In Table 3 different symlet wavelets are used to decompose the noisy synthesis pressure signal and the results of comparison between hard and hardy-square shows the outperformance of the later upon the former if symelet8 is used for the compression process, all other parameter are supposed to be fixed at certain values, such as level 5 and universal threshold selection rule and level dependent estimates of the noise for threshold rescaling principle.

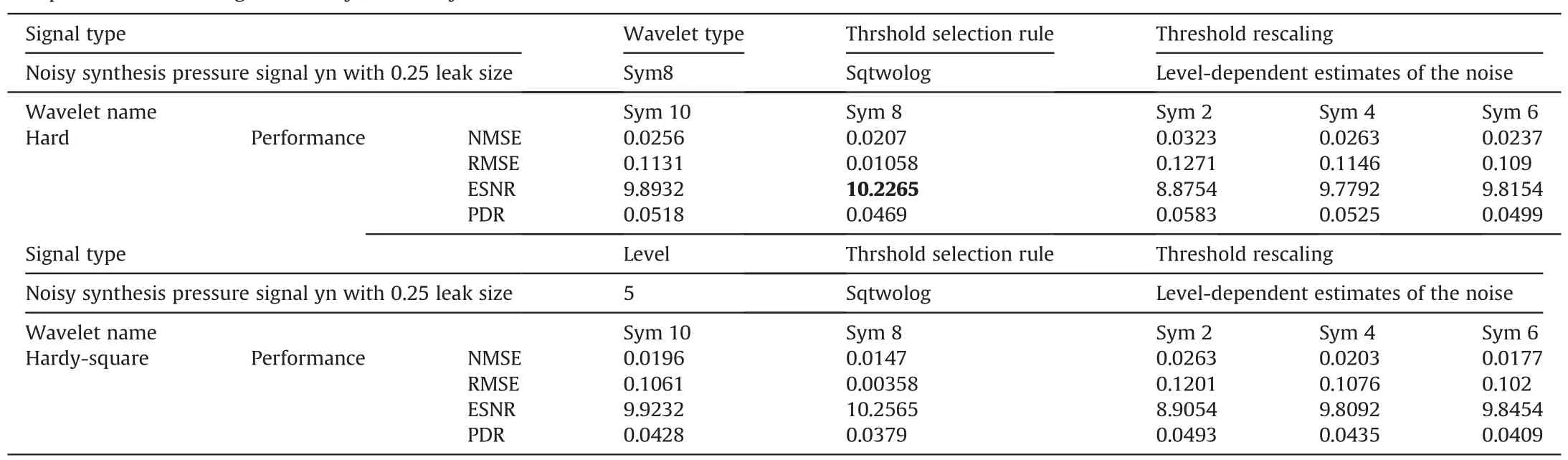
Table 3Compression results using different symlet family wavelet mother functions.

Table 4Compression results using symlet 8 wavelet mother function with different decomposition levels.

Table 5Compression results using symlet 8 for wavelet different threshold selection rules.

Table 4 summarized the results for the level decomposing selection process,where the levels are varied and the performance is examined using the proposed indices and keeping the other parameters that involved in The compression algorithm fixed(such as wavelet type, thresholding method, threshold selection rule and threshold rescaling method).

After the selection of symlet8 as wavelet mother function with level 5 as the best decomposition level for compression the under test pressure signal; now Table 4 examined different threshold selection rule and compare between them to show the best rule among them.From the results at Table 5 it is clear that the proposed hardy-square thresholding has larger ESNR(or lower NMSE,RMSE,and threshold (labeled by sqtwolog), also the results shows the comparison between softy-square and classical soft thresholding for different threshold selection rule. A proposed noisy synthesis pressure signal for a leaked pipeline with 0.25′′is shown in Fig. 2 with its compressed versions using different threshold selection rules. In order to explain the compression comparison analysis Fig.3 through 8 show compression results for different signals with recent thresholding methods (logarithmic, augmented, mixed,improved, and squared-chebyshev) and Stain unbiased risk estimate(SURE) rule (Figs. 4-8)).

6. Conclusions

The work in this paper shows a systematic followed procedure to get the optimal compression results a matlab program had been written to simulate the results for compression a proposed synthesis pressure signal of a pipeline leaked by 0.25′′the compression process involved a comparison between different wavelets from symlet family,and choosing the best mother function among them.Then the procedure continue to select the best decomposing level for the chooser wavelet and finally the comparison occurred between different threshold selection rule and the results of comparison procedure emphasis on the outperformance of the new proposed thresholding method of hardy-square upon the classical hard rather than softy-square and soft thresholding methods using four different performance indices NMSE, RMSE, ESNR,and PDR.

Fig. 2. Signal compression using square thresholding for different threshold selection rules.

Fig. 3. Compressed Noisy Block signal with SURE.

Fig. 5. Compressed Noisy Heavy-Sine signal with SU.

Fig. 6. Compressed Noisy Doppler signal with SURE.

Fig. 7. Compressed Noisy Quadchirp signal with SURE Denoising Noisy Blocks signal with SURE.

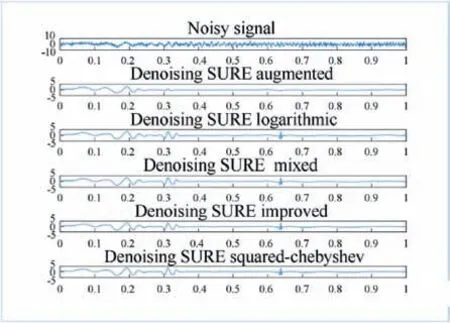
Fig. 8. Compressed Noisy MishMash signal with SURE.