基于CIC滤波器原理的音频信号快速重采样算法
2019-07-16张江安杨洪柏
张江安 杨洪柏
1(上海工程技术大学 上海 200437)2(上海开放大学理工学院 上海 200433)
0 引 言
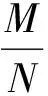
面对上述问题,寻求一种能够应用于嵌入式音频系统的简便而高效的信号重采样算法显得尤为必要。Hogenauer提出的级联积分器和梳状(Cascaded Integrator-Comb,CIC)滤波器[8-11]不仅具有良好的低通特性,而且由于其结构简单、无乘法运算、不需存储滤波器系数等特点,在多采样率信号处理中被广泛应用。在已有的应用中,CIC滤波器较多地被用于信号抽取或内插处理,以整数倍降低或升高信号采样率。文献[12]在通信系统中以硬件电路形式将CIC滤波器用于特定分数倍信号采样率变换,但它并未给出重采样算法,无法在嵌入式系统中应用。本文面向嵌入式系统中音频信号分数倍采样率变换的实际需求,根据CIC滤波器工作原理,提出了一种快速的音频信号重采样算法。首先在分析CIC滤波器结构特点的基础上,构造包含内插和抽取操作的三级CIC重采样滤波器,并根据其工作过程中的信号流得到基本的重采样算法。然后通过简化内插和抽取操作,减小运算开销,得到高效、快速的音频信号重采样算法。该算法不仅能够保持较好的音频质量,而且内存需求少,计算速度快。
1 三级CIC重采样滤波器的构造


图1 三级级联梳状滤波器
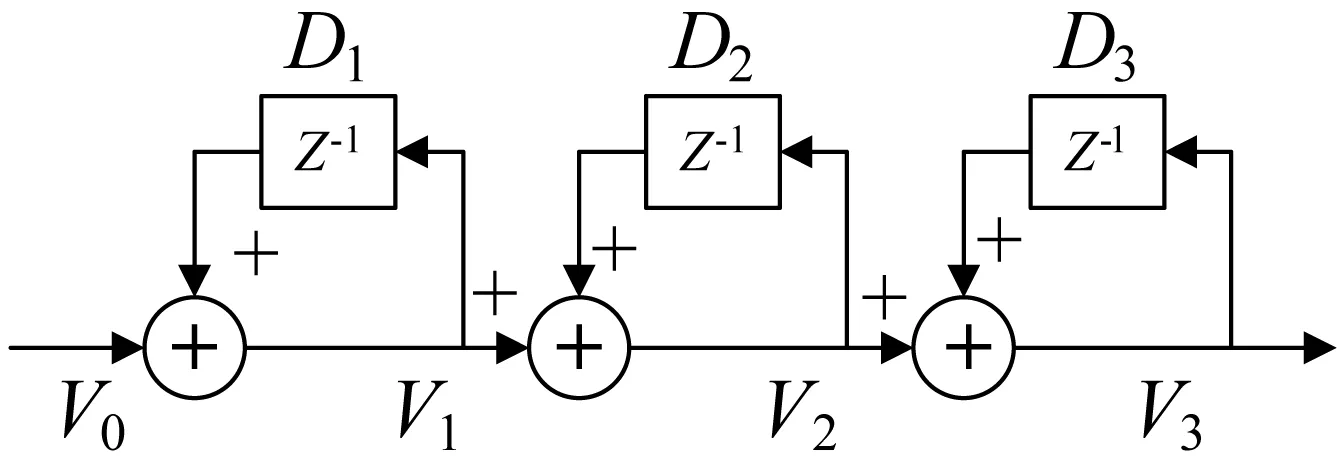
图2 三级级联积分器

图3 三级CIC内插滤波器
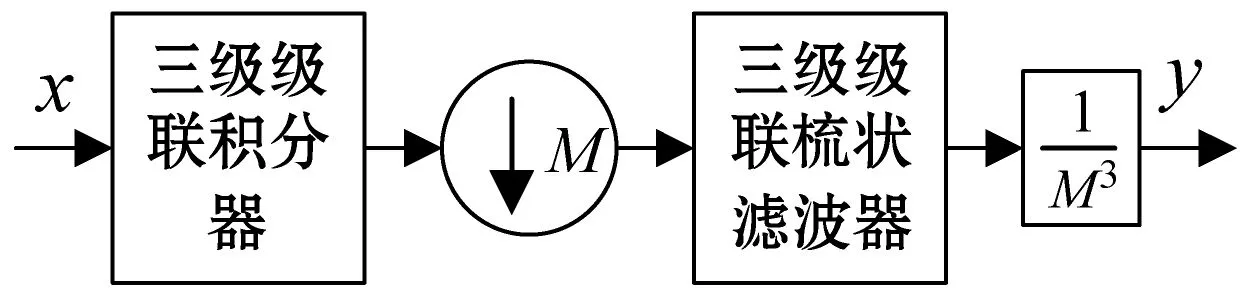
图4 三级CIC抽取滤波器

图5 三级CIC重采样滤波器
2 音频信号基本重采样算法
显然,CIC滤波器级联级数越多,低通滤波效果越好,但滤波器结构也越复杂。三级CIC重采样滤波器结构较为简单,且具有较强低通性能,可满足音频信号重采样处理的要求。根据图1、图2、图5,采用算法形式描述三级CIC重采样滤波器的工作过程,得到如下音频信号基本重采样算法:
Input:x
//输入信号序列
Output:y
//输出信号序列
1.t←0,k←0
//控制变量初始化
2.D1←0,D2←0,D3←0
//寄存器值初始化
C1←0,C2←0,C3←0
//寄存器值初始化
3. Forifrom 1 toLdo
//逐点输入信号
3.1S1←x(i)-C0
//梳状滤波器计算
3.2S2←S1-C1
//梳状滤波器计算
3.3S3←S2-C2
//梳状滤波器计算
3.4C0←x(i),C1←S1,C2←S2
//寄存器值更新
3.5 Forjfrom 1 toNdo
//内插循环
3.5.1t←t+1
3.5.2 Ifj=1 then:V0←S3
//数值传递
Else:V0←0
//零值内插
3.5.3V1←V0+D1
//积分器计算
3.5.4V2←V1+D2
//积分器计算
3.5.5V3←V2+D3
//积分器计算
3.5.6 Ift=Mthen:
//抽取操作
k←k+1,y(k)←V3/N2,t←0
3.5.7D1←V1,D2←V2,D3←V3
//寄存器值更新
4. Return(y)
在上述基本算法中,L为输入音频信号采样数。t是一个决定信号抽取时刻的时钟计数器,其值在0~M之间循环变化。在算法执行之初将其初始化为0。随后每当内插环节插入一个样值0,t值增1。算法运行中,每当t=M条件成立时,抽取V3值并经增益处理后作为算法输出值,同时t值清零。显然,由于内插循环的存在,上述基本重采样算法需要耗费大量的运算时间,效率较低。
3 音频信号快速重采样算法

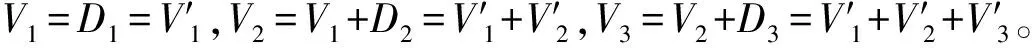
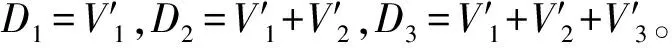
不断重复上述过程可知,对于任意j≤N,可得:
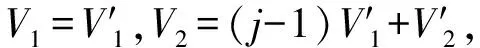
根据步骤3.5.6,当抽取操作发生时:
(1)
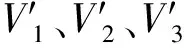
因此,可取消内插循环操作,改为通过式(1)直接计算重采样输出值。为适应此变化,t值更新方式需作相应改变。每当系统输入一个采样值x(i)时,t增加N。每当系统输出一个重采样y(k)时,t减小M(参见步骤3.5.6)。
当t≥M时,将执行重采样信号抽取操作。根据图6可知,此时内插循环计数器为:
j=M+N-t
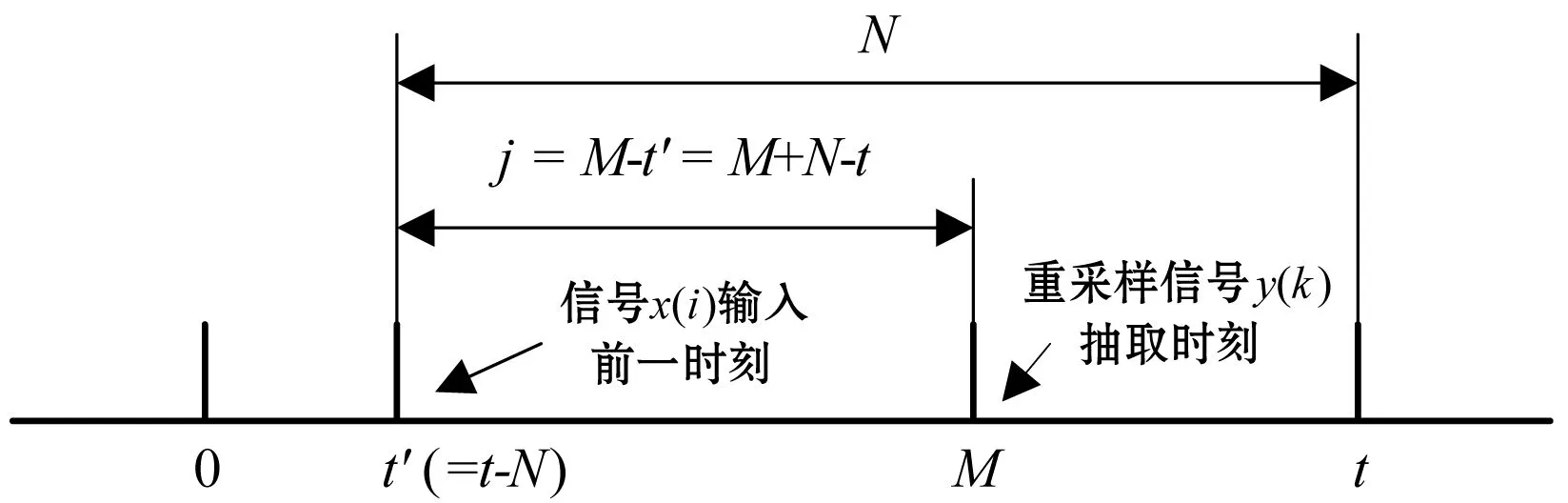
图6 重采样时刻内插循环计数器的计算
参照式(1),得到如下重采样计算公式:
(2)

t←t-M
(3)
随后检查t≥M是否仍然成立。若成立,则说明仍然有信号抽取操作等待执行。重复式(2)、式(3)的计算和操作,直至t 综上,提出基于三级CIC重采样滤波器的音频信号快速重采样算法如下: Input:x //输入信号序列 Output:y //输出信号序列 1.t←0,k←0 //控制变量初始化 2.D1←0,D2←0,D3←0 //寄存器值初始化 C1←0,C2←0,C3←0 //寄存器值初始化 3. Forifrom 1 toLdo //逐点输入信号 3.1S1←x(i)-C0 //梳状滤波器计算 3.2S2←S1-C1 //梳状滤波器计算 3.3S3←S2-C2 //梳状滤波器计算 3.4C0←x(i),C1←S1,C2←S2 //寄存器值更新 3.5V1←D1+S3 //积分器计算 3.6V2←D2+V1 //积分器计算 3.7V3←D3+V2 //积分器计算 3.8t←t+N //控制变量更新 3.9 Whilet>=Mdo //输出值计算循环 3.9.1k←k+1 3.9.2j←M+N-t 3.9.3y(k)←(j(j-1)V1+2(j-1)V2+2V3)/(2N2) 3.9.4t←t-M //t值更新 3.10D1←V1 //寄存器值更新(下同) 3.11D2←(N-1)V1+V2 3.12D3←N(N-1)V1/2+(N-1)V2+V3 4. Return(y) 在上述快速算法中,While循环为计算重采样输出值的循环。由于算法中N为常数, 在上述算法中,可以将除以“2N2”运算转变为乘以“1/(2N2)”的运算,以达到在嵌入式系统中简化计算的目的。从基本算法到快速算法,t值变化的步长由1变为N,重采样计算速度得以加快。上述快速重采样算法的流程图如图7所示。 图7 快速重采样算法流程图 为验证上述音频信号快速重采样算法的有效性,本文在MATLAB平台,对音频信号快速重采样算法进行了大量测试。测试信号由多种类型的音频信号组成,其中语音、歌曲、纯音乐各40段,每段长约3分钟。信号原始频率包括22.05 kHz、32 kHz、44.1 kHz、48 kHz四种规格,每种规格信号总数的1/4。测试在四种不同的采样频率之间进行。通过试听可知,采样频率转换后的音频可以较好地保持原有音频的质量。 图8显示了一段原始音频信号与相应的重采样音频信号波形。原始音频信号的采样率为44.1 kHz,经重采样处理后采样率变为48 kHz。由图8可知,音频信号快速重采样算法能够较好地保持信号的细节,从而保证了转换后的音频质量。 (a) 原始信号片段(采样率:44.1 kHz) (b) 重采样信号(采样率:48 kHz)图8 原始音频信号与重采样信号 本文所提出的音频信号快速重采样算法构建在三级CIC滤波器基础上,其通带增益特性可由下式计算[8]: (4) 式中:f为信号相对CIC内高采样频率的归一化频率。由式(4)可知,A(f)具有滚降特性。当f趋近0时,A(f)趋近1,信号的衰减很小。当f增大时,信号的衰减增大。相对应地,在基于FIR滤波器的重采样方法中,由于FIR滤波器的通带通常被设计得非常平坦,所得到重采样信号的失真将非常小。因此,可将基于FIR滤波器重采样算法(以下简称为FIR算法)的输出音频作为频率转换后的基准音频,对本文提出的基于CIC原理快速重采样算法(以下简称CIC算法)的精度进行对比分析。 (5) 式中:L′为信号长度。 对4.1中实验数据进行误差分析,得到各种类别音频重采样信号的平均信噪比(如表1所示)。由表1可见,CIC算法对包含语音、歌曲和纯音乐在内的各种音频信号均有较好的转换质量。 表1 快速算法输出音频的信噪比 为了对算法的计算开销进行对比,在ADI公司DSP开发平台VisualDSP++3.5上分别实现CIC算法、FIR算法、Farrow结构滤波器算法[4](以下简称Farrow算法)。结果表明,CIC算法的计算开销远远小于其他算法。以转换前后采样率分别为44.1 kHz、48 kHz(N=160,M=147)为例。表2、表3分别列出了这三种算法的计算量和存储空间需求。表3中,ROM用于存储滤波器系数,RAM用于存储中间数据。当需要支持更多转换倍率时,CIC算法不需要增加存储空间,而其他两种算法则需要增加ROM空间。 表2 计算量对比(由44.1 kHz转换为48 kHz) 表3 存储空间对比(N=160,M=147) 由表2、表3可见,CIC算法在计算开销方面相较于FIR算法和Farrow算法具有极大的优势。 基于三级CIC滤波器原理的音频信号快速重采样算法具有计算速度快、占用存储空间少、输出音质较好的特点,特别适合于在计算资源少、低成本的嵌入式音频播放系统中以软件形式实现,具有很高的性价比。当然,该算法仍有一定改进空间。将CIC滤波器级数升级为四级,将在增加少量计算开销的情况下进一步提高输出音频的质量。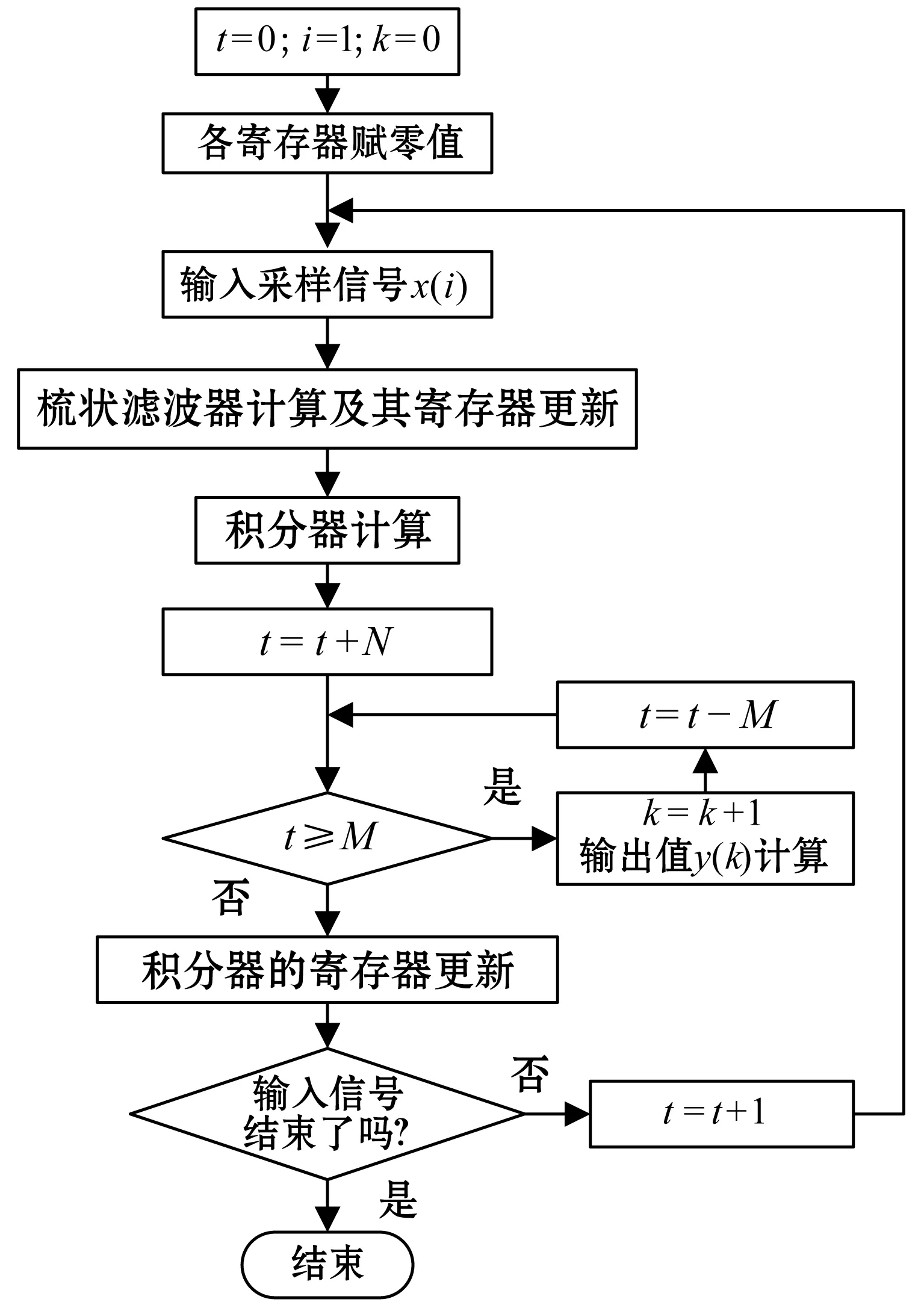
4 测试与分析
4.1 主观测试
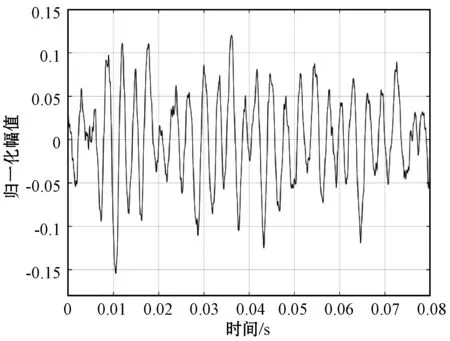

4.2 误差分析


4.3 计算开销分析


5 结 语
