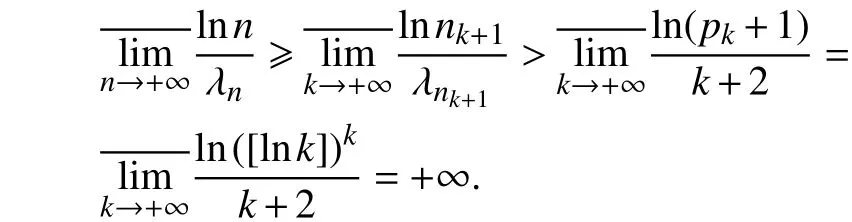Dirichlet级数的广义级

陈青远，霍颖莹

（广东工业大学 应用数学学院，广东 广州 510520）

1 基本介绍

考虑Dirichlet级数:

关于Dirichlet级数的增长性和值分布，国内外学者进行了长期的研究并取得了一系列的成果[1-4]， 其中包括许多与整函数有关的研究. 例如，M.N.Seremete[5]研究了快速增长的整函数的广义级和广义型，G. Kapoor与A. Nautiyal[6]为慢增长的Taylor整函数定义了广义级，孔荫莹和甘会林[7]定义并分析了由慢增长的Dirichlet级数所定义的整函数的广义级与广义型. Dirichlet级数的增长性由它的级和型来衡量，关于全平面上Dirichlet级数增长性的研究成果[8-11]多数基于以下两个条件:

和

文献[12]在条件

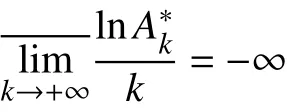
下，采用Knopp-Kojima方法获得了全平面上Dirichlet级数的最大模、最大项及系数之间的一些关系. 本文在较弱的条件下得到了与文献[12]相同的结果，并提出了一个条件，在上述的两个条件下可将上述结果转化为由Dirichlet级数定义的整函数的广义级与系数之间的关系.

为了确定Dirichlet级数的收敛域，常用Valiron公式来计算各种收敛横坐标，其中

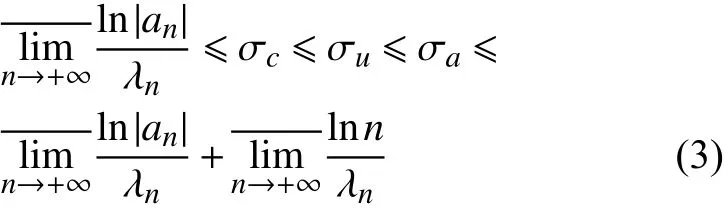
而Knopp-Kojima[13]给出了求Dirichlet级数的3种收敛横坐标确切值的公式，方法如下:

如果 [k,k+1)∩{λn}= ∅，那么令 Ak=A∗k==0，得到分别关于 Ak，Ak∗，的横坐标σc，σa，σu的公式，

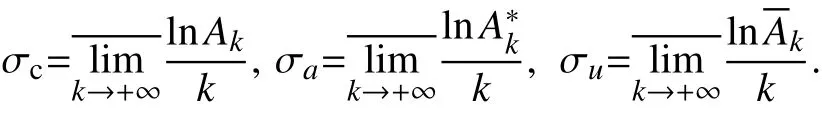
定义1 对级数(1)，假设 σu＜+∞，当σ＞σu时，定义

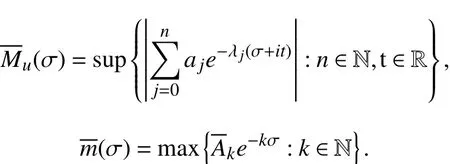
接下来介绍慢增长的Dirichlet级数的广义级[7]，让Λ 表示一组函数α (x)，满足下列条件:

(1) α (x)为定义在[ a,+∞)上正的严格递增的可微函数，且当 x→+∞时α (x)→+∞.

(2)

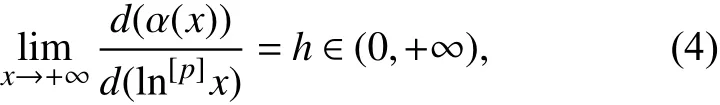
其 中 p≥1， p∈ ℕ+，ln[0]x=x,ln[1]x=lnx,···,ln[p]x=ln[p-1]lnx.

定义2 设 α(x)∈ Λ，定义Dirichlet级数(1)的广义级为

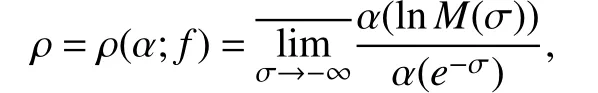
其中 M(σ)=sup{|f(σ+it)|:t∈ ℝ}.

本文要证明以下定理:

(1) 当p=1时，

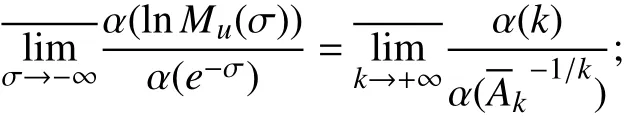
(2) 当 p=2,3,···时，

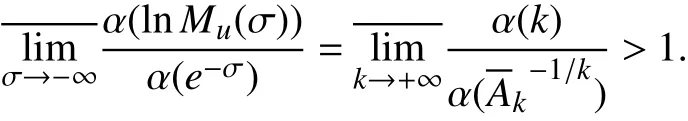
令

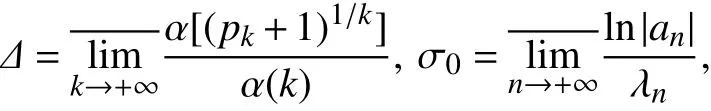
其中 pk由定义.

(1) 当p=1时，

(2) 当 p=2,3,···时，

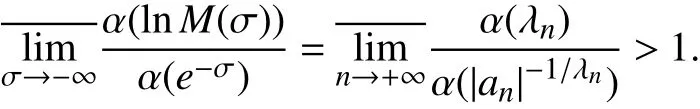
推论1 设Dirichlet级数(1)满足条件 σu=-∞与(2)式，则

(1) 当 p=1时，

(2) 当 p=2,3,···时，

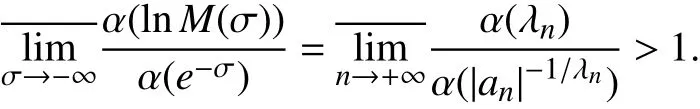
注:文中例5.1表明条件Δ =0弱于条件(2).

2 几个引理

引理1 若α (x)∈ Λ，则

(1) 对任意的正数c 有，

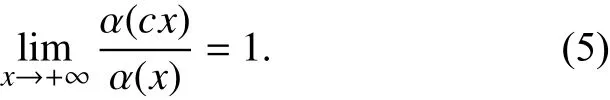
(2) 当 p=1时，对于任意实数 A，

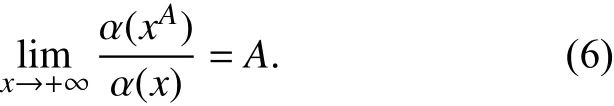
(3) 当 p=2,3,···时，对于任意的0 ＜A1,A2＜B1和B＞1有，

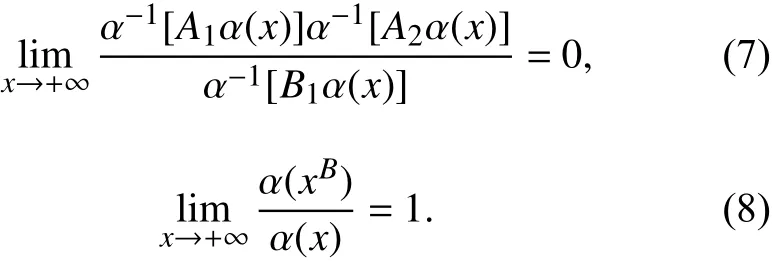
证明 因 α(x)∈ Λ，由等式(4)可得

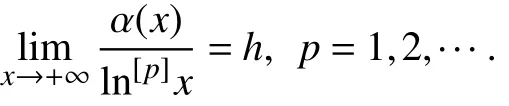
对固定的 p 和充分小的正数ε ，存在 M＞0，对于任意的 x＞M有，

也就是

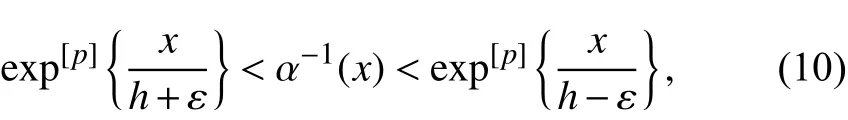
证明的余下部分读者可参阅文献[12]和[14].

引理2[15]设Dirichlet级数(1)满足条件 σu＜+∞，对任意的σ ＞σu，下面的结论成立:

(1) 对于任意的正整数n ，| an|≤ M(σ)eλnσ；

引理3 设Dirichlet级数(1)满足条件σu=-∞，对于每个α (x)∈ Λ有，

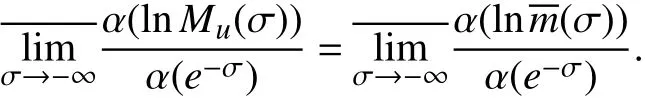
证明 证明与文献[14]的引理2.3的类似，因而在此不予证明.

引理4[15]设是一正的常数，是任一实数. 那么函数

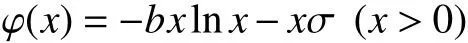
3 定理证明

3.1 定理1的证明

证明 因条件 σu=-∞，由引理3可知可取代定理1中的令

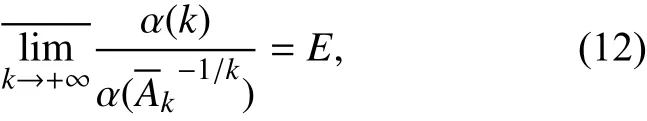
那么对任意δ ＞0，当k 充分大时，有

从而可得，

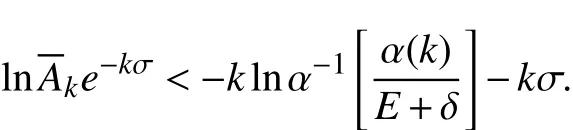
下面将证明分为两种情况完成.

情况Ⅰ:当 p=1时，首先证明

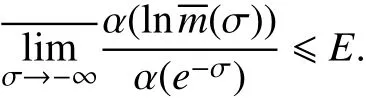
由式(11)有，

再由引理4可得，

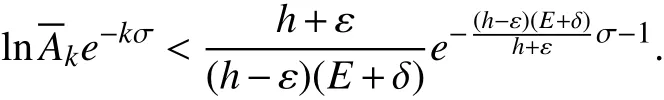
应用式(5)和式(6)，就有

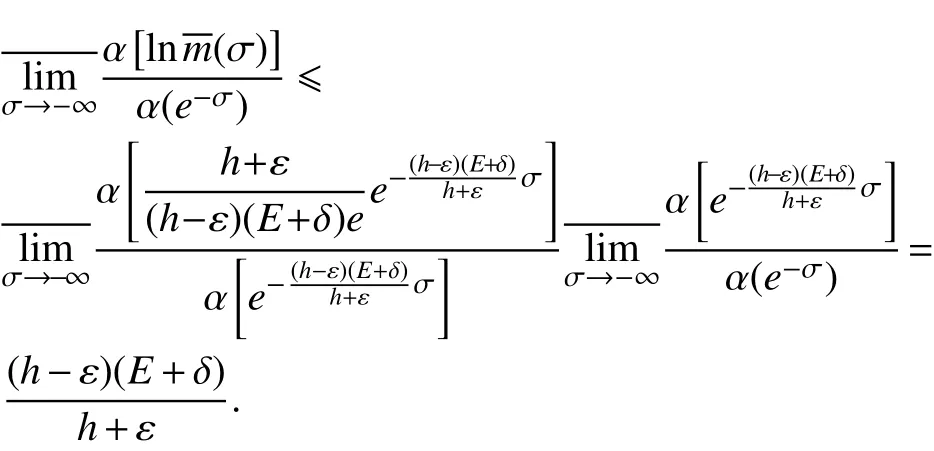
因此，

假设上式中等号不成立，则

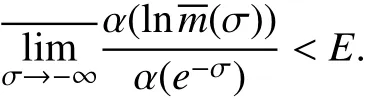
那么存在 ε0＞0，使得对充分大的- σ和任意的正整数 k，

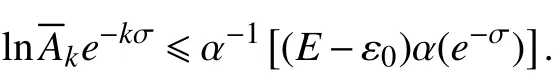
由式(11)得，

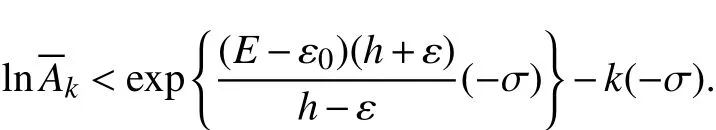
令

于是

应用式(9)，有

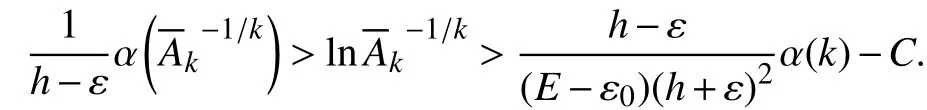
由此可见，

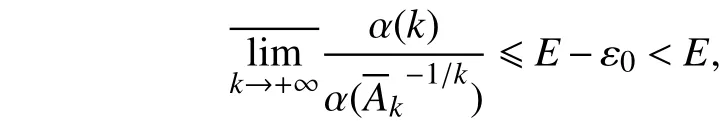
这与式(12)相矛盾.

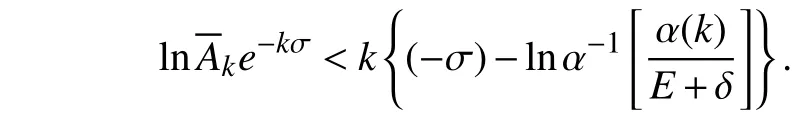
首先，证明

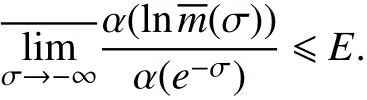
否则有k (-σ)＞ H，于是

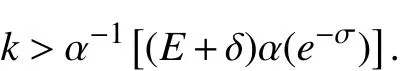
从而有，

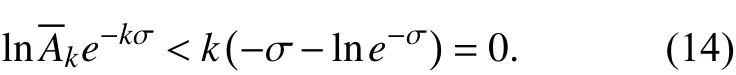
结合式(13～14)，于是对任意正整数 k有，

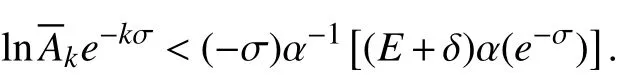
由此可知，

由式(7)得，

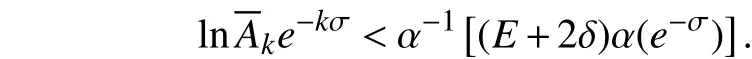
于是

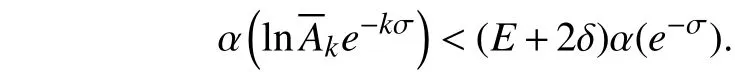
从而有，

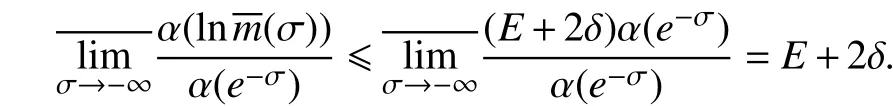
因此，

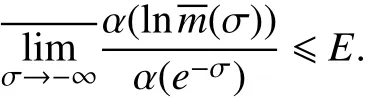
最后，需证明

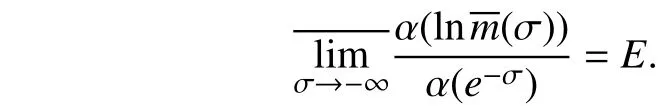
假设

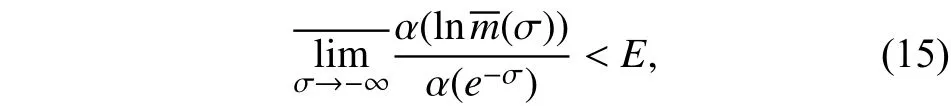
通过式(15)可证得

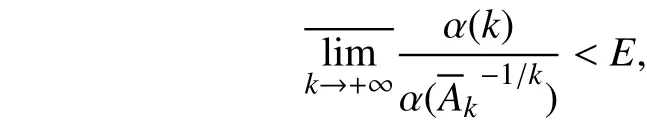
与等式(12)矛盾，定理立刻可得.

如果不等式(15)成立，那么存在 ε0＞ 0，当- σ充分大时，

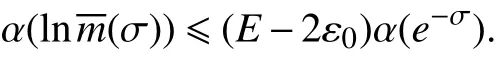
则对任意的正整数k ，

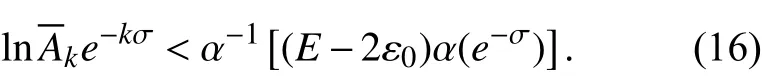
因为σu=-∞，从而有

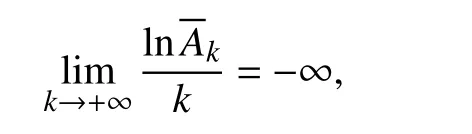
由此可得，

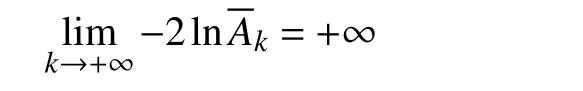
与

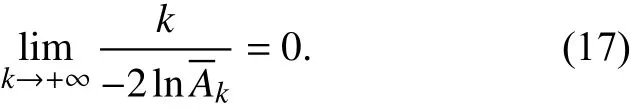
令

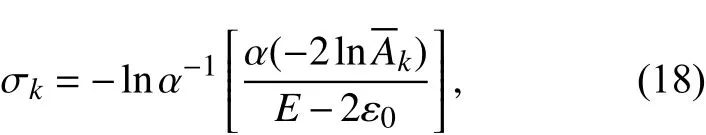
则

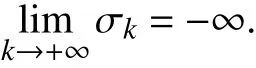
结合式(16)与式(18)可知，当k 充分大时，

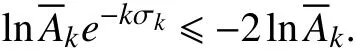
即

于是

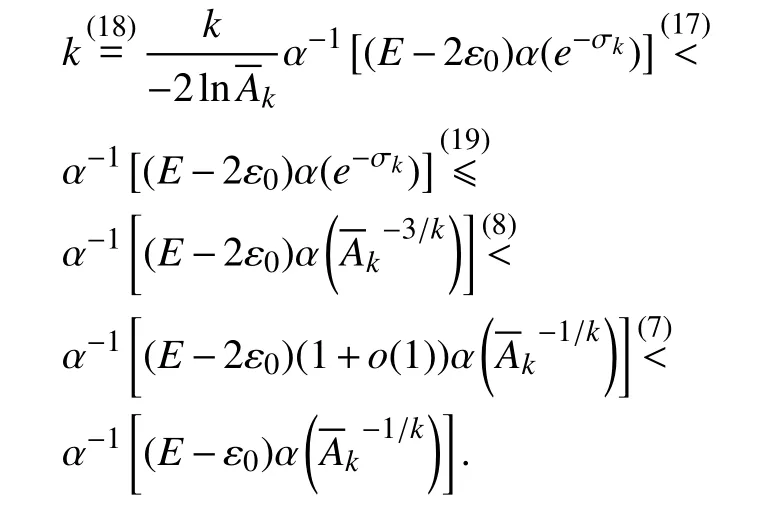
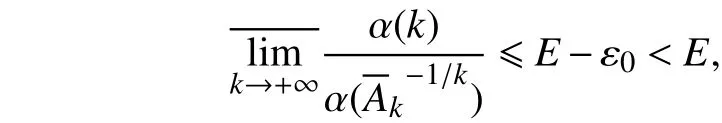
因此，与等式(12)产生矛盾.由以上两种情况本文完成了定理1的证明.

3.2 定理2的证明

证明 设

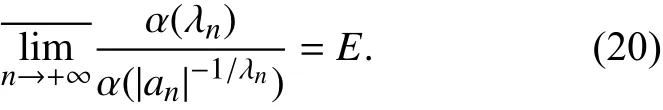
下面将证明分为两步完成.

第1步:不论 p取何值，首先证明

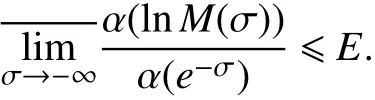
由于 σu=-∞且，可从定理1中注意到以下事实

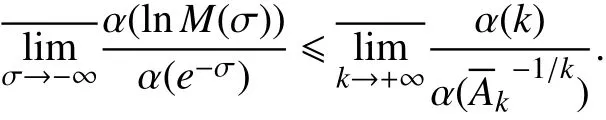
因此，只需证

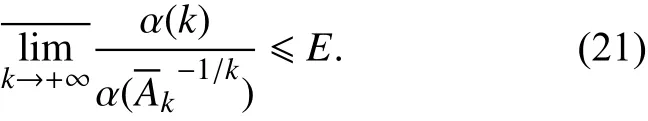
由式(20)，对任意 δ＞0，存在正整数 N0，使得对于任意n ＞N0，有

于是

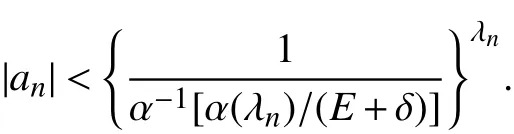
那么当k ＞N0时，

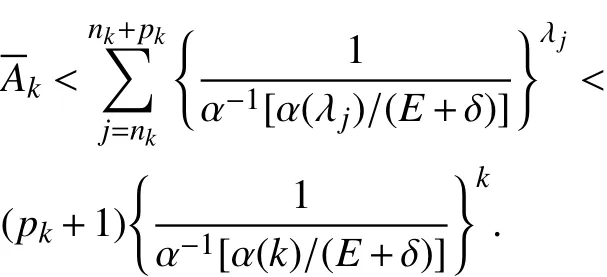
由条件 Δ=0，对于充分小的ε ＞0，存在正整数N1，使得对任意k ＞N1时有，

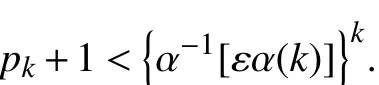
当k＞max{N0,N1}，

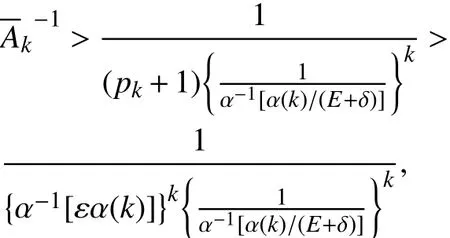
即

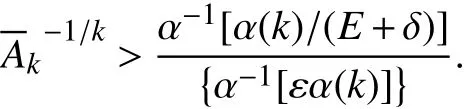
情况Ⅰ:对于 p=1，由式(11)知，

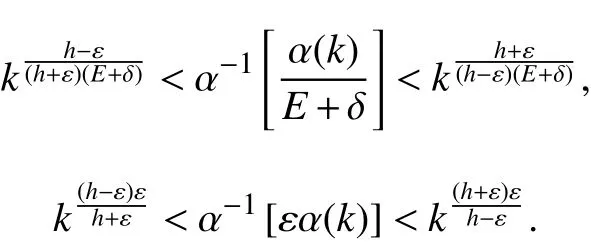
于是

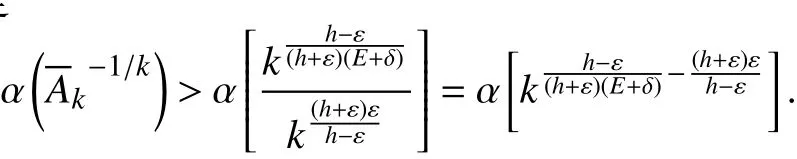
应用式(6)可得，

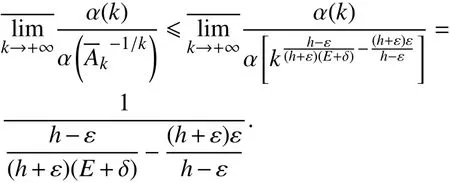
因此，

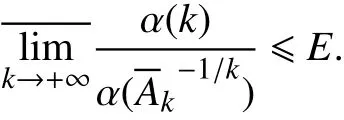
情况Ⅱ:对于 p=2,3,···，由式(7)知，对任意正数M，总存在正整数N2，使得对于任意k ＞N2，

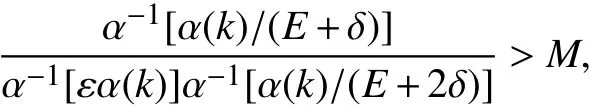
即

令K=max{N0,N1,N2}，当k ＞K时，

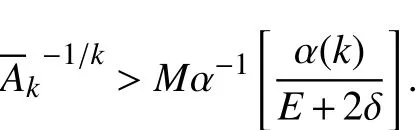
于是

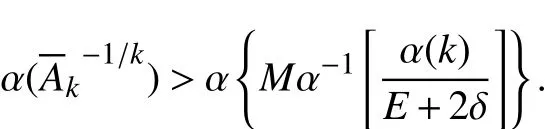
由式(5)可得，

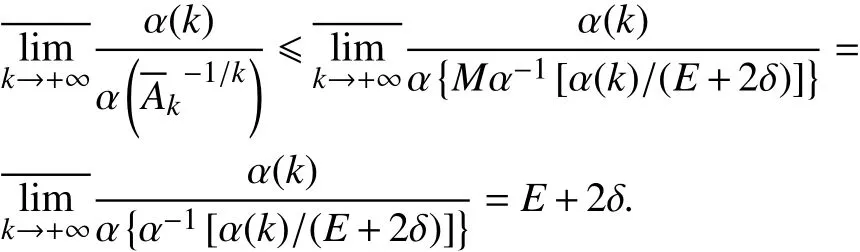
由δ 的任意性，就有式(21).

第2步:下面证明

假设

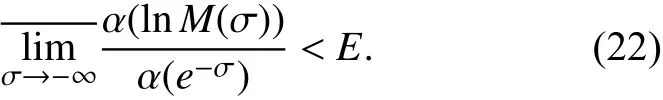
定理将通过式(22)可证得

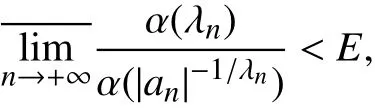
与等式(20)矛盾而得证.

情况Ⅰ:对于 p=1，由式(22)，存在ε0＞ 0，使得对充分大的- σ有，

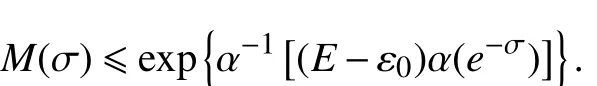
根据引理2的(1)，对于上述的σ 与任意的正整数n 有，

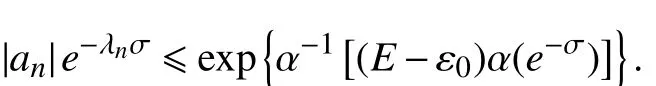
再由式(11)可知

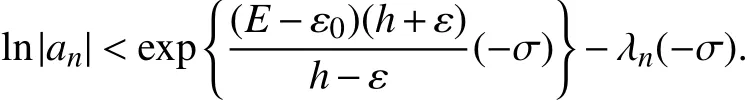
令

于是

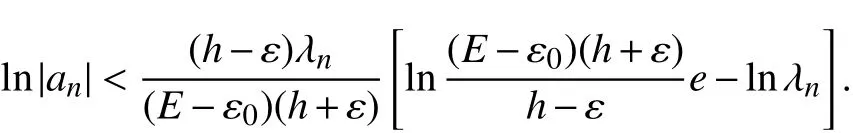
应用不等式(9)即得

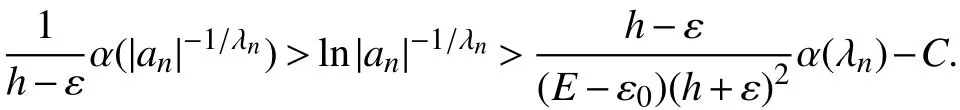
由此可得

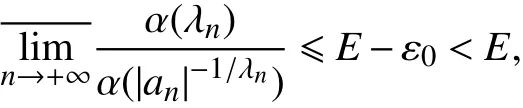
这与式(20)相矛盾.

情况Ⅱ:对于 p=2,3,···，如果不等式(22)成立，那么存在ε0＞0，当- σ充分大时，

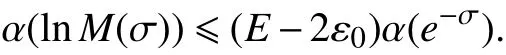
对于任意的正整数n ，有

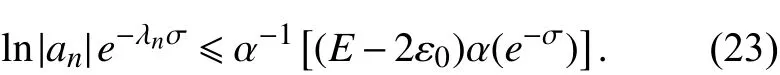
由于σu=-∞，再由式(3)可知

则有

且

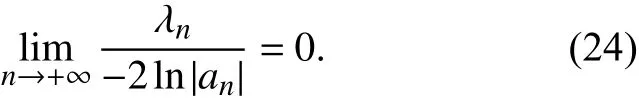
令

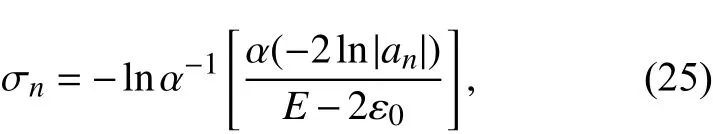
则

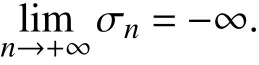
从而结合式(23)和式(25)可知，当n 充分大时，有

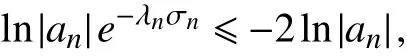
即

于是

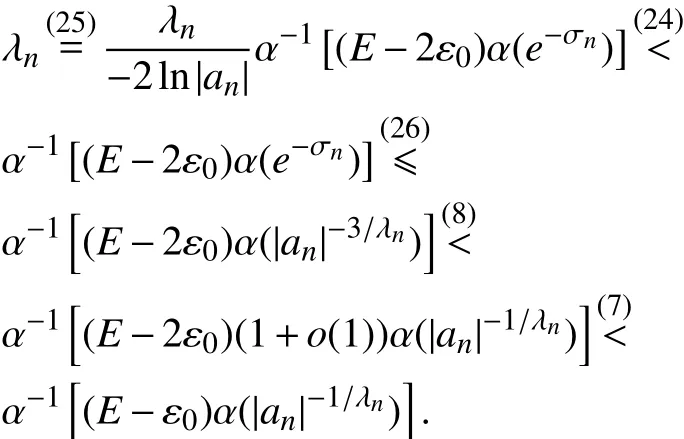
因此，

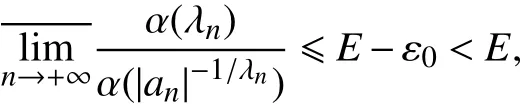
这与式(20)产生矛盾.

由以上两个步骤定理2即得证.

4 推论证明

证明 由于

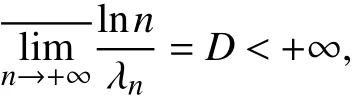
那么对于任意ε ＞0，当正整数 n充分大时，

于是

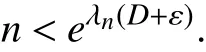
则当k 充分大时有，

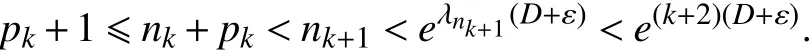
由此可得，

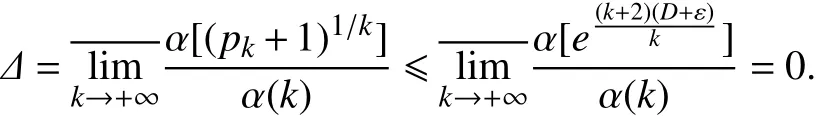
因此， Δ=0. 又因σu=-∞，根据定理2可知推论成立.

5 例子

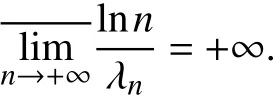
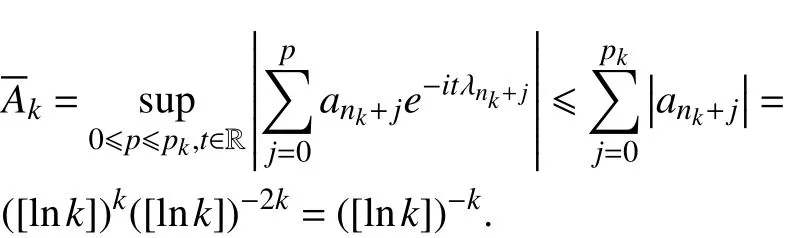
则有

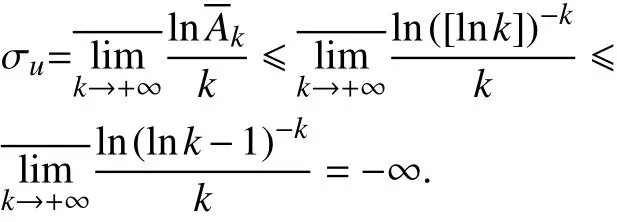
再由Δ 的定义可得，

但是，