一种基于线阵相机的报靶系统解算模型研究

陈新元，张国豪，罗 齐

（1.空军勤务学院航空弹药保障系，江苏 徐州 221000；2.94303部队，山东 潍坊261000；3.95178部队，广西 南宁530028）

0 引言

各类武器射击中，实际应用的弹着点定位方法有光电探测定位法，声电探测定位法，基于图像处理的定位法等[1-3]。光电探测定位法是以光电转换技术为基础，探测飞行弹丸到达空间指定位置时刻的方法，通过光电元器件探测到变化的光信号，转换为电信号，然后再传递给信号处理系统，经过计算处理，即可得出弹着点的位置，实现对弹丸弹着点的探测[4]。声电探测定位法是各声音传感器以一定形式安装在同一面内，近似可认为激波在靶平面内是以恒定速度传播，当弹丸产生的脱体激波传播到声音传感器时，电信号会产生，根据传感器的位置和获取到的各传感器的信号，通过构建空间模型，即可解算出弹着点的位置。基于图像处理技术的弹着点定位方法是一种集现代计算机技术、网络传输和数据库设计技术、图像采集和处理技术于一体的系统集成方案。利用图像采集系统对靶面进行图像采集，利用阀值规则对图像分割，靶面中某点具有最大的灰度值，即唯一确定为靶心，当靶面上有弹孔时，其灰度值不同于其他地方的灰度值，从而可以被准确得判别出来[5，6]。

当前几种对高速小目标探测的方法，通过运用不同的原理、采用不同的方案，可实现不同情况下弹丸的探测定位，每种方法都有一定的优点。但是，由于机载火炮对地打靶训练发射平台机动性较大、弹丸散布面积较大、弹丸速度较高和发射方式较多等，利用上述几种方法对弹着点的探测比较困难、局限性较大，因此，亟需一种新的探测报靶方案。

鉴于此，基于线阵相机工作原理，本文提出一种通过相机拍摄、像素采集、模型建立以及空间解析计算的方法，来实现机载火炮对地攻击训练弹着点的精确报靶。

1 基于线阵相机的报靶系统解算模型

在进行机载火炮对地攻击训练时，靶场上要事先设置靶环供飞行员瞄准射击。该解算模型为，在距离靶环一定位置布置四台性能相同的线阵相机，建立靶场坐标系和相机坐标系。在进行打靶训练时，用线阵相机拍摄弹丸弹道，然后通过像素采集和空间解析计算的方法解算出理论弹着点。

1.1 坐标系的建立

以靶心为坐标原点o，过o点中心弹道在靶平面（可以是水平面或一定坡度的斜平面）的投影为ox轴，且与中心攻击方向一致为正；oy轴过o点垂直于靶平面，方向朝上；oz轴垂直于oxy平面，方向由右手法则确定，见图1。在离靶心一定距离的位置上布置四台性能相同的线阵相机。相机1、2的位置点对称分布在中心弹道在水平面投影的两边。相机1、2组成的相机坐标系相对地面坐标系的偏航角为y12=0°，俯仰角为 J12，相机 1、2 分别按照顺时针、逆时针转动角度g1、g2。由于线阵相机的探测区域为通过相机光轴线的一个平面，所以相机1的探测面和相机2的探测面重合。其中a为中心弹道入射角，当俯仰角J12=90°时，探测面为铅垂面。当俯仰角J12=90°-a时，在一定探测距离下，探测范围最大，如图1所示。

图1 靶场坐标系示意图

1.2 相机坐标系与靶场坐标系的转换

图2 为相机坐标系角度关系示意图。相机T12坐标系 o′x′y′z′：设相机 T1、T2的探测面共面，相机 T1、T2位置中心为坐标原点 o′，过原点 o′相机 T1、T2位置的连线 o′z′为轴，在共面内垂直于 o′z′轴的为 o′x′轴，o′y′轴由右手法则决定。设相机T12的中心在oxyz坐标系中坐标为o′（x*12，y*12，z*12）。相机坐标系o′x′y′z′相对坐标系oxyz的姿态关系：

俯仰角 J12：o′x′轴与靶平面 oxz 的夹角，o′x′轴从下向上穿过靶平面为正，反之为负；

偏航角y12：o′x′轴在靶平面 oxyz上的投影与 ox轴的夹角，由ox轴逆时针方向转至投影线方向时为正，反之为负；

滚转角 g12：o′x′轴与包含 o′y′轴的垂直平面的夹角，沿o′y′轴方向看，相机由垂直平面右转为正，反之为负。

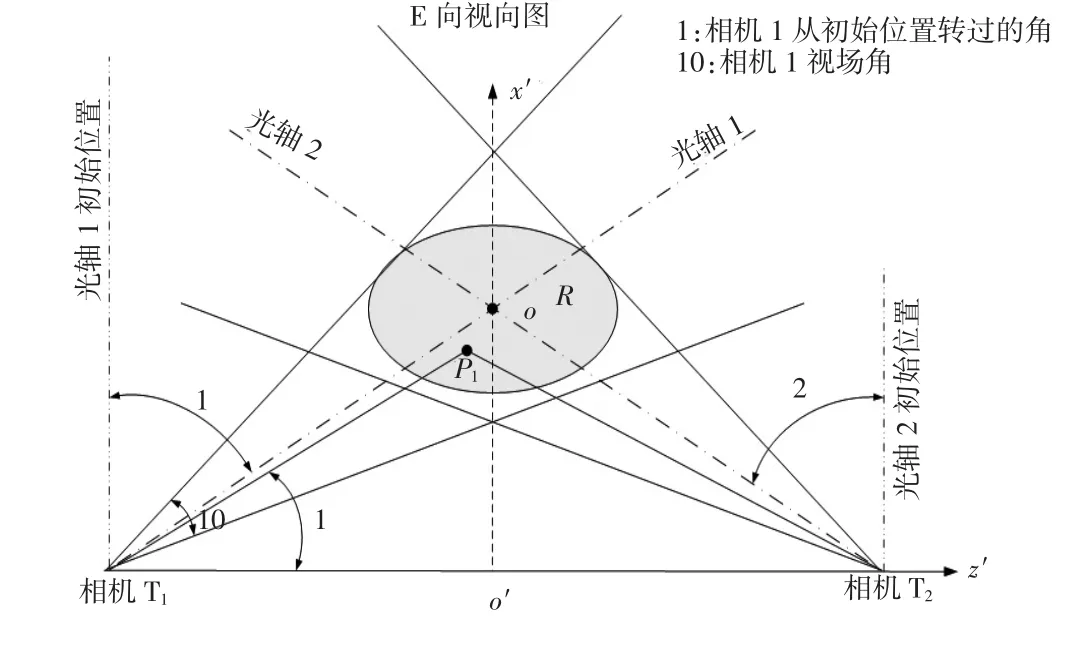
图2 相机坐标系角度关系示意图

如图3为相机内部结构简图，AB为相机内部成像面，C为相机镜头中心，虚线CD为相机光轴，光线CA，CB通过镜头中心，P*为探测点P1在相机成像面上的像。

图3 相机内部结构简图

鉴于位置量对弹丸定位不是很敏感，将位置量作为常量，故在相机 T12坐标系 o′x′y′z′的探测面 o′x′y′上，弹道与探测面的交点P1（即探测点）在相机T1中形成的射线方向倾角a1为：

其中，S*为探测面上的弹着点在相机1中的像素大小，S1为相机T1的分辨率，a10为相机1的视场角，为光线 P1P*与光轴的夹角。

则射线 T1P1在相机 T12坐标系 o′x′y′z′中的方程为：

其中，T12为相机T1、相机T2之间的间距。

同理，可得射线 T2P1在相机 T12标系 o′x′y′z′中的方程为：

解方程（2）与（3），可得探测点 P1在坐标系o′x′y′z′中的坐标为：

探测点P1在坐标系o′x′y′z′中的坐标）与靶场坐标系oxyz中的坐标P1（x1，y1，z1）的转换

关系为：

式（5）中，当相机1、2与靶心处于同一水平面上，并且相机1、2的位置点对称分布在中心弹道在水平面投影的两边，则相机T1、T2的对称中心在靶场坐标系oxyz中的坐标。其中转换矩阵如下：

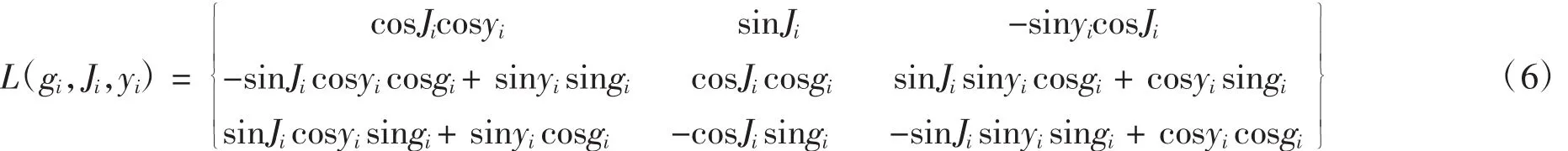
L 式（6）中，当相机为 T1、T2时，i=1，2；当相机为T3、T4时，i=3，4。

同理，可得相机T3，T4决定的探测点P2（x2，y2，z2）。那么，弹道方程为：

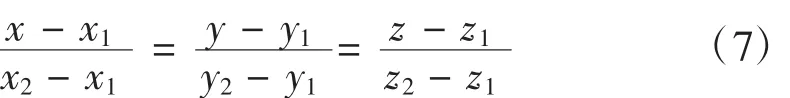
在式（7）中令y=0，可得弹着点坐标为

2 实验验证及系统误差分析

2.1 实验验证

本实验利用面阵相机模拟线阵相机进行探测，图4为该模拟实验示意图。实验准备工作如下：（1）选取六组模拟弹着点，用绳子模拟弹道；（2）标定4台相机最大视场角；（3）建立地面坐标系：oxyz；（4）建立中心弹道：使中心弹道在地面的投影与ox轴重合。使4台相机沿ox轴对称分布，记录4台相机的坐标值；（5）调整相机的滚动角为0°。在俯仰上调整相机，使中心弹道上的对称点分别在对称相机的图像中心，通过相机的坐标和中心弹道上对称点的坐标推算出相机的俯仰角。整理记录：通过测量得出4台相机的视场角，坐标值以及相机坐标系相对地面坐标系的俯仰角、偏航角、滚动角。实验过程：四台线阵相机姿态和位置标定后，选取六组弹着点，每组弹着点对应一条模拟弹道，通过相机拍摄、像素采集、模型计算处理每组数据，得到每组实际弹着点对应的理论弹着点，如表1所示。

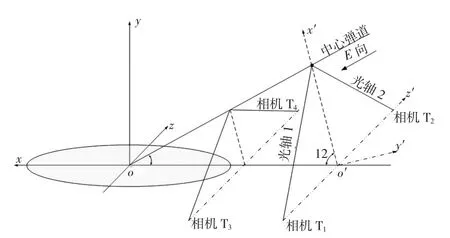
图4 模拟实验示意图

表1 理论弹着点计算结果

通过六组实验中，实际弹着点和理论弹着点的比较，可以得出：通过模型计算出的理论弹着点与预先选定的实际弹着点存在偏差，但在一定误差范围内，可认为实际弹着点与理论弹着点相对一致，能够满足精度要求，通过一定的误差处理方法即可减小误差。

2.2 误差分析

任何系统在探测过程中总会存在着误差，本系统也不例外。本报靶系统定位误差的大小由系统固定误差和随机误差引起的。

2.2.1 系统固定误差来源

本报靶系统的固定误差主要由打靶训练时，弹丸爆炸对相机姿态的影响。由于弹丸爆炸时，相机震动在一定程度上会影响相机的姿态参数，从而造成误差。此误差是固定的，即在系统状态正常、不出现任何故障以及外界环境良好的情况下，系统一旦固定，可以采取系统标定的方法对误差进行修正；系统安装位置误差可以根据靶场特点寻求最佳安装位置，在对系统元器件安装位置确定后，通过多次校准可以减小。在实际靶场打靶训练时，该报靶系统需要在相机周围采取减震措施，来减小误差。在采取减震措施之后，系统固定误差对系统造成的影响很小且几乎是固定不变的。因此，为了提高系统测距定位精度，减小随机误差的影响是研究的重点。

2.2.2 系统随机误差来源

系统随机误差即每次探测定位中，大小都会随距离等因素而变化的误差，主要包括测量误差和定位误差。定位误差即对测量数据进行处理的数据处理方法引起的误差，根据数据特征采取相适应的数据处理方法可减小定位误差。方法处理得当，则定位精确，误差较小，一般采用特异值数据处理和线性回归数据处理等方法来减小随机误差。

3 结语

本文介绍了一种基于线阵相机工作原理的打靶训练报靶系统弹着点解算模型，通过一定的靶场布置、线阵相机拍摄模拟弹道、像素采集，空间解析计算等方法推算出理论弹道，并与实际模拟弹着点比较。通过多组模拟实验，分析计算结果，可得该模型能够客观反映弹着点规律，采取一定的误差处理方法可提高系统精度。该解算模型为报靶系统的实现提供了理论依据。