基于组件树结点属性的静态手势分类
2019-07-15杜树林邱卫根
杜树林,邱卫根
(广东工业大学计算机学院,广州 510006)
0 引言
作为一种自然的交互手段,手势交互是一种应用广泛的人机交互方式,手势识别是实现手势交互不可或缺的关键技术,基于计算机视觉的手势识别是机器视觉领域的一项重要的研究内容[1]。
作为数学形态学理论及方法的进一步发展,组件树[2]方法通过阈值截集产生连通分量,并构造其上的层次树关系,发展出一系列高效的基于树的图像处理算法。组件树是一类应用广泛的连通算子,它通过合并图像的平坦区域而实现形态学滤波,它既不会使图像产生新的轮廓,也不会使轮廓的位置发生改变。因此,它们具有非常好的轮廓保持特性,能够用于基础的图像滤波和高级的对象识别任务等。组件树被广泛应用于对象识别[2]、图像分类[3]、车牌的检测、跟踪与识别[4]等领域。
基于组件树的对象识别和分类的方法,通常首先构建图像的组件树,然后提取组件树的结点属性特征,最后结合先验知识设定阈值条件对图像中符合条件的对象进行识别和分类。本文提出一种针对静态手势图像的分类方法,该方法首先采用高效的灰度图像组件树构建算法对手势图像建立组件树;由于原始图像通常存在大量噪声,组件树的结构相对复杂,存在大量叶子结点,因此采取基于组件树的图像滤波方法对图像进行滤波,再对滤波后的图像建立组件树并对组件树做进一步简化;在此基础上,提取组件树结点的属性,并对组件树结点的梯度属性和面积属性进行分析,找出对应于图像中手部的组件树结点;然后提取上述结点的其他属性信息,并构成此手势图像的特征向量,同时将特征向量存储在数据集中;最后采用全连接的神经网络训练分类器,通过实验检验该分类器的分类效果。
1 组件树相关理论
1.1 组件树的定义
设f:Ω→V是规则域Ω上的图像,具有完全预序集(V,≤ )上的值,并且令N为Ω上的邻域。设λ∈V,把集合p∈Ω,f(p)≤λ记为[f≤λ]。设X⊂Ω,把X相对于邻域N的连通分量集记为CC(X)⊂P(Ω),P(Ω )是Ω的所有可能子集的幂集。记CC([f=λ] ),λ∈V为灰度级λ下的连通分量,则Ψ=CC([f≥λ]),λ∈V是灰度不小于λ的连通分量的集合。由于包含关系,Ψ可由树结构表示,这种树结构即组件树。这种树结构被称为连通分量树(Connected Component Tree)[5],简称组件树(Component Tree)。图1所示是一个灰度图像组件树的例子。

图1 灰度图像组件树示例
在上述定义中,组件树的叶子结点存储局部最大灰度值,因此这种树结构也被称为最大树(max-tree)。根据对称性,如果用像素值小于给定阈值的点的集合来构成连通分量,则叶子点存储局部最小值,这种树结构就被称为最小树(min-tree)。最大树(或最小树)的结点通常只保存某一特定灰度值的点,最大树是组件树去除重复元素后的紧凑版本,最大树能够有效节省存储空间。通常,在设计算法和应用程序时考虑完整的组件树,而在进行运算和处理时采用更高效的最大树结构。组件树与最大树之间的关系如图2所示。
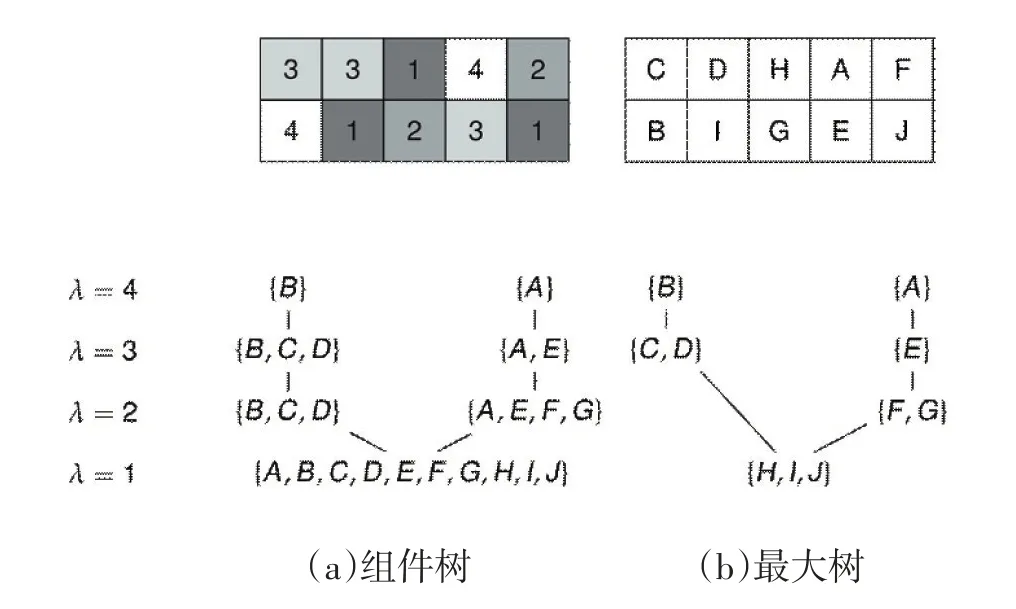
图2 组件树与最大树
1.2 组件树结点属性
组件树本身足以进行某些图像变换,但是对于图像滤波等更复杂的图像处理任务,则需要有关每个组件的一些汇总知识。这些知识由组件树的结点属性表示,所谓结点属性就是表征每个结点的数值。相关文献中常见的一些组件树结点属性如下:
●面积(area):结点所包含的像素个数总数,在3D图像中,这个数目又被称为体积(volume);
●最小值(minimum):结点中各像素的灰度最小值,也被称为水平(level)或者海拔(altitude);
●最大值(maximum):与最小值相对应,即结点中的最大灰度值;
●高度(height或range):结点中灰度最大值与最小值之间的差;
●深度(depth):与二叉树的定义类似,它表示组件树中结点到根之间的距离。
1.3 组件树的构建
自组件树理论形成以来,许多高效的组件树构建和处理算法以及用以提取组件树结点的属性的高效算法被相继提出[6]。按算法所使用的数据结构,可以将建立灰度图像组件树的算法分为两大类,即基于优先队列的算法和基于并查集的算法。本文采用Berger等人[7]提出的算法建立手势图像的组件树。建树算法首先对图像中的点按灰度值逆序排序,然后按照并查集的思想依次为每个点建立一个新的集合作为组件树的一个结点,根据选定的邻接规则查找已经处理的邻域点所属集合(即父结点),如果当前点与邻域点分别属于两个不同的集合,则将它们合并到一个结点,最后再将生成的组件树做正则化处理。算法的伪代码如图3所示,其中f表示灰度图像,R、parent和zpar是和f大小相同的数组,R存储结点的顺序,parent用以保存图像中每个点对应的父结点,zpar是建树过程中用于寻找父节点时保存额外信息的数组,undef表示未定义,实际应用中可将其值取为-1。FIND-ROOT(x)

1.4 组件树的滤波和简化
受光照、采集设备、背景等多方面的因素影响,自然图像中不可避免地存在噪声,而组件树对噪声极为敏感,因此自然图像的组件树通常具有非常复杂的结构,结点数量成千上万,其中存在大量的叶子结点和面积很小的非叶子结点。对于图像处理任务来说,使用原始的组件树是不现实的[1]。
实际应用中,通常需要选取滤波规则,对组件树做一定的简化。首先选择适当的连通规则(4邻接或8邻接)构建图像的组件树,然后根据大小或形状等滤波条件移除组件树中的部分结点,最后根据简化后的组件树重建图像。相对于中值滤波器和均值滤波器会对图像造成模糊的不良影响,基于组件树的区域开操作能够很好地保持图像的轮廓特性同时不会造成图像模糊,并能够去除噪声。图3展示的是组件树滤波方法对图像进行滤波操作的结果,图3(a)是带有椒盐噪声的原始图像,图3(b)是对组件树中面积小于25的结点过滤后重建的图像。

图3 组件树滤波
为了简化组件树同时不丢失相关信息且保留拓扑结构,Souza等人提出了最大组件树简化方法(Maximal Max-tree Simplification,MMS)[3]。MMS 方法是一种非常实用且高效的组件树简化方法,通常能够大幅减少组件树结点的数量,并且保留图像中最重要的部分。对于在手势图像中寻找手势目标,MMS方法能够大幅减少遍历时间。
1.5 组件树结点属性计算
对手势图像建立组件树之后,接下来的工作是计算组件树的结点属性特征。为便于属性数据保存和结点遍历,本文采用Souza等人[8]提出的一种基于数组的面向结点的最大树表示方法,这种方法使用两个数组,即存储结点属性的结点数组(Node Array,NA)和表示每个像素所属结点的结点索引(Node Index,NI)。结点数组和结点索引能够方便高效地从上一节所用算法的返回值(R,parent)生成。
实验中,考虑到手势图像的轮廓特性和计算复杂度,本文所采用的组件树结点属性除结点面积和高度之外,还使用了以下几个特征:
●矩形比(Rectangularity Ratio):结点对应连通分量的面积与其外接矩形面积之间的比值;
●离心率:结点对应图像区域的离心率;
●形心:结点对应图像区域的形心位置;
●长宽比:结点对应图像区域外接矩形长和宽的比值;
●区域位置:结点对应区域外接矩形的顶点位置。
2 实验
2.1 数据集
本文的实验中所采用的数据集包括两部分:手势图像数据集和组件树结点属性数据集。
手势图像数据集来源于Jochen Triesch静态手势数据集(JTD)[9],由24个人在3种不同的背景(明、暗和复杂)下各作10个手势,共计720张图像,图像大小为128×128像素。图4为该数据集中的部分示例图像。由于实际应用中通常使用最大树来表示组件树,因此本文选取暗背景的图像进行实验。

图4 JTD中的手势图像示例
结点属性数据集为自建数据集。基于上一节提出的组件树构建算法和结点属性提取方法,对JTD数据集中的暗色背景图像建立组件树,采用基于组件树的区域开操作对图像进行滤波及MMS方法对组件树做简化,然后提取简化后的组件树中对应于手势部分结点的属性,最后保存提取的属性特征向量到结点属性数据集中。数据集的样本随机打乱次序后,按8:2的比例划分训练集和测试集。
2.2 分类器的训练
本文的实验采用全连接神经网络,网络深度为8,输入层为图像组件树得结点属性,各隐藏层的神经元个数分别为 64、128、256、512、256 和 128,输出层为分类结果。由于结点的不同属性在数值上差异较大,因此先将各属性的数值做归一化处理。
实验中,采用随机梯度下降法,训练过程中动态调整学习率,激活函数为ReLU。训练10000代之后,分类准确率趋于稳定,在参数量仅为330K的情况下,分类的平均准确率达95.83%。
3 结语
本文采用一种称为组件树的树形结构来表示图像,定位树结构中的关键结点并提取其属性特征,并将该特征作为图像的特征描述,最后通过训练全连接神经网络对组件树的结点属性特征进行学习,作为分类依据。作为一种高效的数据结构和图像表示方法,组件树结构能够很好地表达图像中的层次关系,方便提取图像中的连通区域。由于图像中包含大量的冗余信息,直接在图像上使用CNN的方法包含了许多不必要的计算,增加了计算量,而使用组件树的方法去除了图像中的大量冗余信息,同时又保留了图像的关键特征。实验结果表明,本文提取的组件树结点属性能够较好地作为图像的特征并用于图像分类任务。
