城市轨道交通运营补贴与定价博弈研究

陈 群，李文峰，陈 哲

CHEN Qun1, 2，LI Wenfeng1, 2，CHEN Zhe1, 2

（1.福建工程学院 管理学院，福建 福州 350118；2.福建工程学院 建筑产业现代化管理研究中心，福建 福州 350118）

(1.Management School， Fujian University of Technology， Fuzhou 350118， Fujian， China；2.Research Center for Management of Construction Industry Modernization， Fujian University of Technology， Fuzhou 350118， Fujian， China)

0 引言

由于城市轨道交通具有公共属性，运营投资额巨大，仅依靠票务收入难以维系城市轨道交通运营公司的正常运营，因而需要一定的政府财政补贴。然而，不合理的补贴与定价机制不仅加大了政府的财政压力与公众的选择倾向性，还将造成运输效率大幅降低，无法充分彰显其实际价值。可见，城市轨道交通运营阶段的补贴与定价问题已成为制约其可持续发展的关键要素之一，研究博弈视角下的城市轨道交通运营补贴与定价问题具有较强的现实意义。

现阶段城市轨道交通运营补贴研究主要与政府考核机制和运营补贴机制相挂钩。通过考核手段确保政府提供的财政补贴机制更为规范、高效，以提高运营公司的运营效率及服务水平[1-2]。除此之外，陈贤军[3]分析得出基于行车公里数的补贴模式较为合理，但由于不同时段运力水平不同、政府难以合理分析运营公司的实际运营现状等原因，导致该补贴模式难以为继。此外，运营定价与企业的资金管理密切相关，其管理水平的高低直接影响企业的营运能力[4]。在运营定价研究中，动态定价研究占据多数。Jong[5]发现不同定价将对乘客的出行方式选择产生显著影响，并提出了基于客流量的动态定价模型。李静、田贵超、易欣等[6-8]均针对公共交通的分时定价展开研究。唐文彬等[9]研究了城市轨道交通与传统公共交通之间关于定价问题的合作博弈，并从城市轨道交通运营公司与乘客2个方面展开分析，为城市轨道交通与传统公共交通的定价机制优化提供了一定的参考依据。

城市轨道交通的补贴与定价彼此间相互影响，存在极大的关联性。在目前城市轨道交通补贴与定价研究中，针对二者的研究相对独立，集成研究较为匮乏。为此，综合考虑补贴、定价与客流量三者之间的关系，构建政府与城市轨道交通运营公司的Stackelberg微分博弈模型，并以福州地铁为例进行综合分析，以进一步完善城市轨道交通补贴与定价机制研究。

1 城市轨道交通运营补贴与定价博弈模型

Stackelberg微分博弈模型可用于在时间连续的系统内，解决博弈过程中信息不对等的博弈双方，在一方做出相应决策的情况下，另一方根据对方决策情况进行相应决策的博弈分析行为，力求各自独立、冲突的目标最优化，最终求得各参与者随时间演变策略的纳什均衡。

1.1 模型假设

假设 1：城市轨道交通运营公司与政府为博弈的2个参与方。假设双方在博弈过程中都保持理性状态，且在一定运营服务水平下补贴与定价成功与否完全由博弈参与方决定，暂不考虑其他可能的影响因素。

假设 2：为保证研究的顺利开展，假设城市轨道交通运营公司与政府间在一定程度上不存在信息不平衡的情况，即政府对于城市轨道交通运营公司的服务水平、运营票价及大致运营成本有一定程度的了解，城市轨道交通运营公司对政府的财政补贴额度也相对明确，即认为该博弈是在双方信息完整的情况下进行的。

假设 3：在博弈阶段，由政府首先做出博弈决策，该阶段的最终博弈决策是为了达到社会效益最大化。假设政府对城市轨道交通运营公司给予的财政补贴额度依据运营服务水平与定价因素，设人均补贴额度为f，客流量为λ，则相应补贴总额为fλ。

假设 4：在博弈的第二阶段，城市轨道交通运营公司根据政府所提供的补贴方案进行服务水平及定价方面的决策调整，该阶段的最终博弈决策结果是在保证一定社会效益的前提下，尽可能地提高运营定价，进而实现经济效益最大化。

假设 5：假设一定服务水平s下，政府方的城市轨道交通运营理想定价P与客流量λ之间存在以下函数关系

式中：P为城市轨道交通运营定价；λ为城市轨道交通客流量；a与β为相关系数。

假设 6：假设城市轨道交通运营公司的总运营成本函数为

式中：c1与c2均为成本系数；c0为城市轨道交通运营的固定成本；c0≥0，c1＞0，c2＞0。

假设 7：在受到其他有关因素的影响下，城市轨道交通运营定价的微分状态方程函数表达为

式中：p为城市轨道交通运营最终定价；公式(1)中a-βλ为在合理控制范围内，政府方的城市轨道交通运营理想定价；p-a+βλ为最终定价与理想定价之间的差值；ζ为微分状态方程中的调价系数。

1.2 模型求解

政府的目标函数为

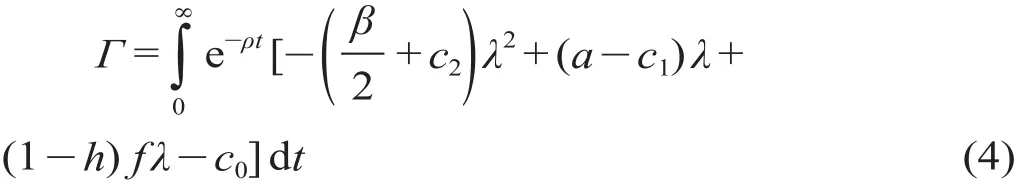
式中：Γ为有界、连续且可微的政府价值函数；ρ为贴现率；h为消费者剩余中的影响系数。

轨道交通运营公司的目标函数为

式中：τ为有界、连续且可微的城市轨道交通运营公司价值函数。

1.2.1 第二阶段模型求解

首先，将城市轨道交通运营公司的二次值函数设为V(p) =θ2p2+θ1p+θ0，V '(p) = 2θ2p+θ1。θi(i= 0，1，2)为所设相关系数。因此，城市轨道交通运营公司的HJB方程如下。

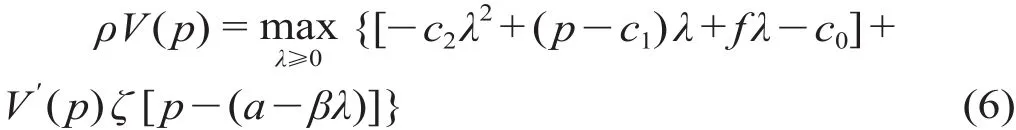
将上述方程最大化，得到城市轨道交通运营公司在一定服务水平下提供的客流量λ的表达式为

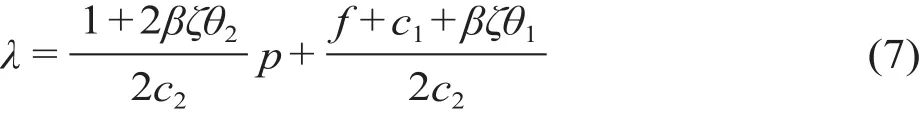
根据上式结果，通过待定系数法求得θ1和θ2的表达式，如下所示。

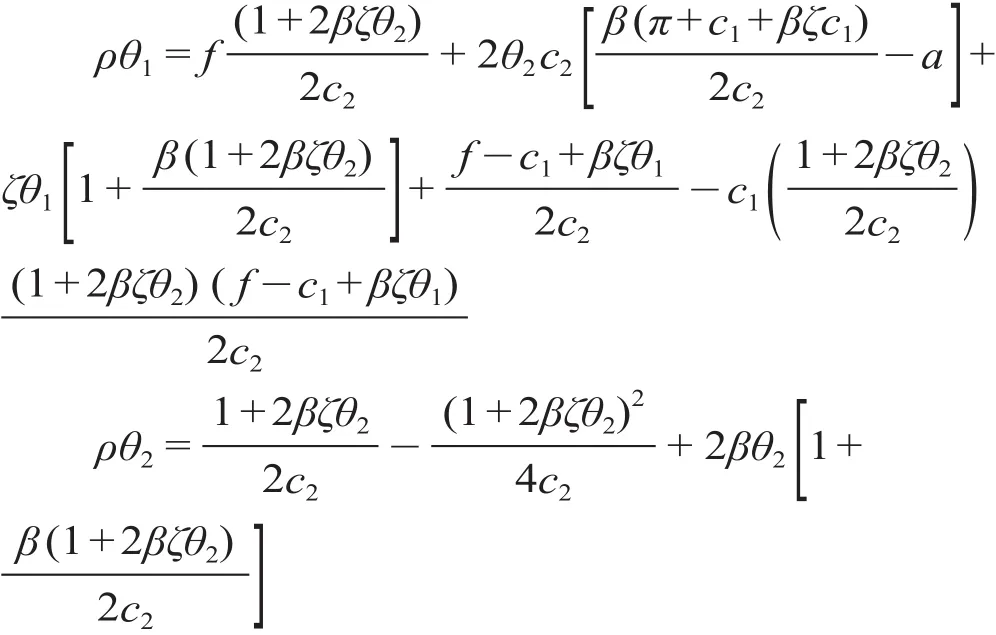
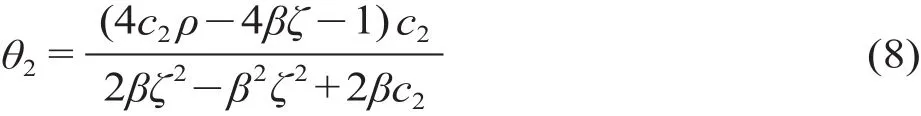
通过式子ρθ1与ρθ2可求得二次值函数式和θ2的表达式(8)，为求得θ1表达式，简化之后假设θ1=k1+k2f，求得待定系数k1，k2。

接着，将V '(p) = 2θ2p+θ1、θ1=k1+k2f代入公式(7)中，求得城市轨道交通运营公司在一定服务水平下的决策函数表达式如下。

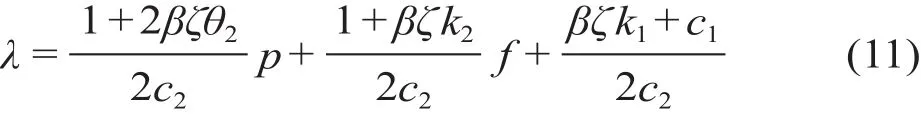
1.2.2 第一阶段模型求解

政府的二次值函数设定为L(p) =μ2p2+μ1p+μ0，L '(p) = 2μ2p+μ1。μi(i= 0，1，2)为所设相关系数。因此，构建政府的HJB方程如下。

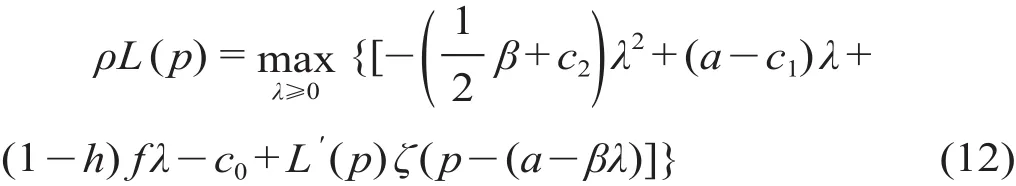
由公式(11)可知城市轨道交通运营公司的最优客流量决策，并将最优客流量决策代入公式(12)中，得到政府视角下的HJB方程解。

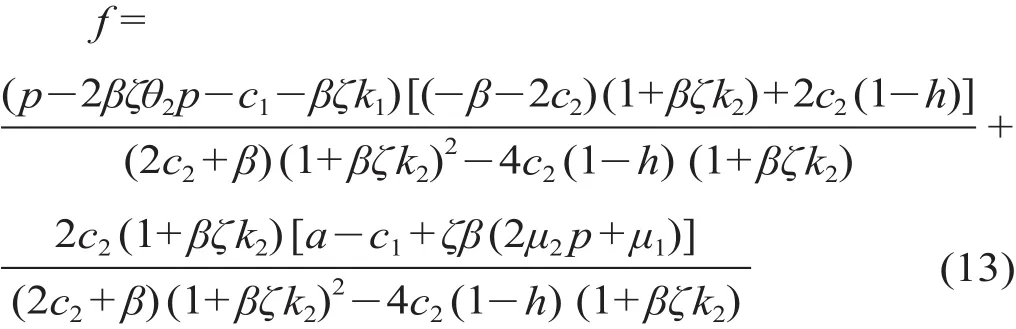
在关于f的函数表达式中，在求得k1，k2，c1，c2，β，ζ，λ，μ1，μ2等函数值后，城市轨道交通运营公司能够获得最大化的政府财政补贴。其中，c1，c2，β，ζ，λ通过专家调查分析方法总结得到，k1，k2，θ2由上式求得。将f用含m与n的表达式表示为f=m+np，通过待定系数法求得m，n的表达式如下所示。

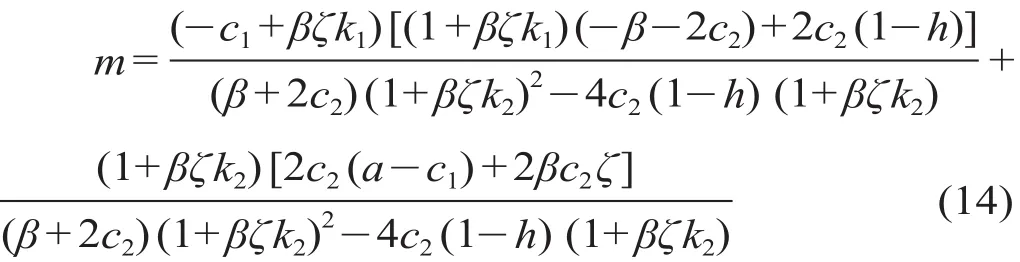
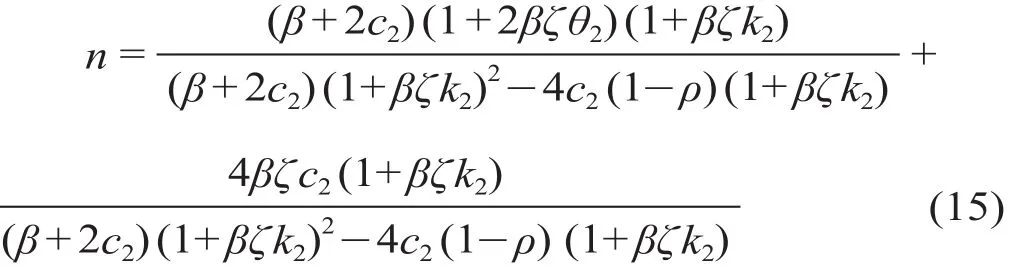
将L '(p) = 2μ2p+θ1和f=m+np代入 HJB 方程得到

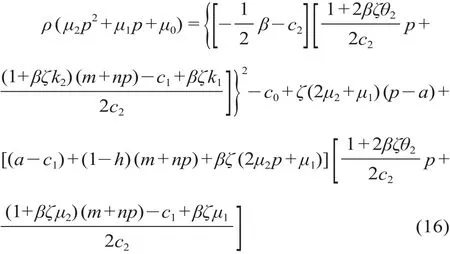
根据政府补贴的HJB方程，与第二阶段的模型求解相同，通过待定系数法确定价值函数L(p)和L'(p)系数的μ1和μ2的值，具体如下式所示。

模型均衡解联立政府补贴的决策变量f，城市轨道交通运营公司在一定服务水平下的客流量λ及定价p的微分状态方程，其中c1，c2，a，ζ，ρ，β依据城市轨道交通运营过程中的调查数据总结获得，θ2，k1，k2，m，n通过上述表达式求得。

可求出p，λ，f关于时间t的函数如下。

2 实例分析

以福州地铁为例，对其运营定价与客流量以及政府财政补贴的关系进行分析。福州地铁1号线于2016年5月开始运营，线路总里程为24.89 km。在轨道交通网络体系、轨道交通运营管理等方面均存在不足，亟待改善。在确定相关外生变量初始值方面，通过实地调研及专家访谈等方式开展工作，并结合合作单位提供的现实数据，对运营服务水平、客流量等方面进行梳理、分析。

由于福州地铁尚处在发展初期，运营时间较短。在案例分析中，各变量初始值的取得一方面是通过调研直接获得，另一方面是通过调研对数据进行分析获得。在确定了各变量初始值后，针对各外生变量对p，λ，β产生的影响主要是基于理论研究，并结合部分实际情况展开分析。首先将相关系数a与地铁现实运营服务水平相联系，通过实地问卷调查获得运营服务水平得分s为80，且设a= 0.1 s。基于乘客调研情况，其中票价因素所占权重约为0.124 7。在后续研究中对β进行等比折算，令β取值在0.001到0.01之间，故在研究中假设相关系数初始值a= 8，β= 0.001；其次，为保证地铁的运行效率，政府财政对地铁运营补贴高达50%，同时调价系数ζ与政府的实际补贴力度息息相关，调价系数越高则政府的补贴力度越大，ζ取值范围在0到1之间，结合相关合作单位提供的数据，在研究中假设调价系数初始值ζ= 0.5；再次，根据中国城市轨道交通协会统计分析报告，福州地铁年均运营成本约为62亿元，结合调研结果并进行多次假设分析后，城市轨道交通运营公司运营成本函数的参数基本满足c1= 5，c2= 0.05，c0= 50 000；最后，消费者剩余系数、贴现率则依据文献分析获得，分别假设h= 10，ρ= 15。

最终确定各外生变量初始值：a= 8，β= 0.001，ζ= 0.5，c1= 5，c2= 0.05，h= 10，ρ= 15。并基于假设对各变量间相关关系展开分析，以求得不同情况下的补贴、定价情况。

2.1 p，q，λ 之间的相关关系

首先，基于对福州地铁现实情况的数据收集、整理，分析城市轨道交通运营定价p与客流量λ以及政府财政补贴f的关系，将外生变量数值a= 8，β= 0.001，ζ=0.5，c1= 5，c2= 0.05，h= 10，ρ= 15代入公式(7)以及f=m+np中，可以获得λ和f在一定p取值范围内的函数图像。城市轨道交通定价与内生变量间的关系如图1所示。

从图1可知，客流量λ随着运营定价p的增加而减少，同时政府对城市轨道交通运营公司的财政人均补贴额度随着运营定价p的增大而降低。可见，在城市轨道交通运营服务水平维持不变的情况下，多数乘客仍选择传统公共交通。若定价越高，则客流量越低，进而会阻碍城市轨道交通的健康发展。

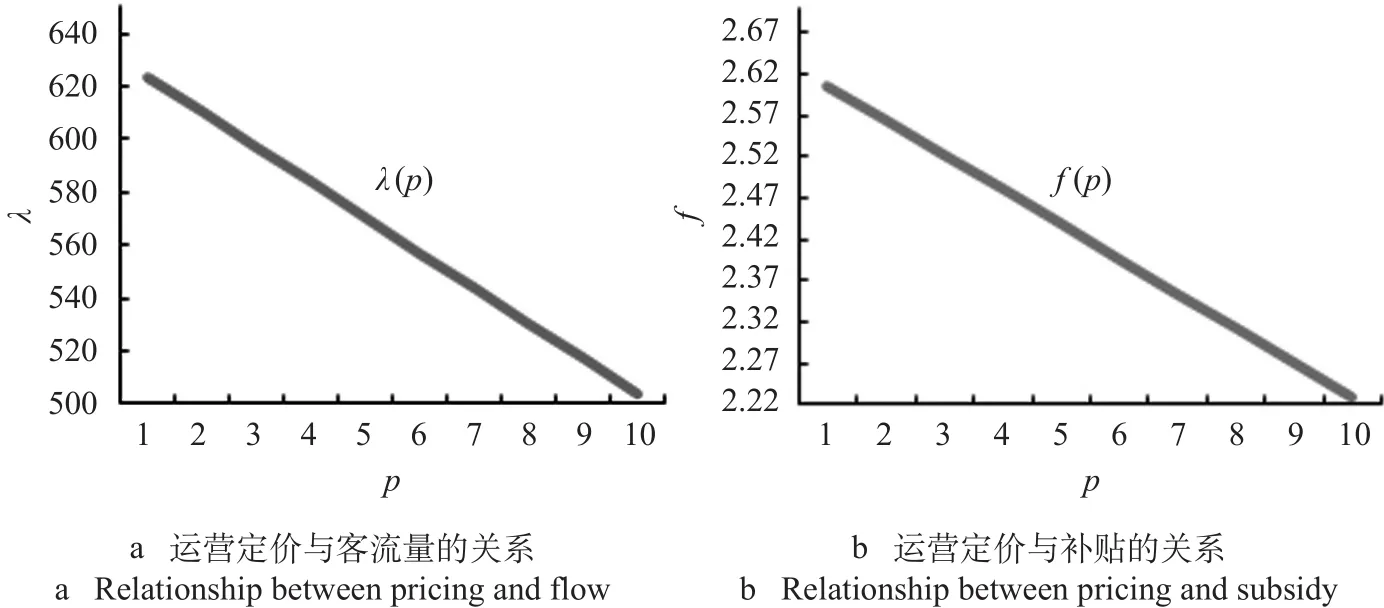
图1 城市轨道交通定价与内生变量间的关系Fig.1 Relationship between urban rail transit pricing and endogenous variables

2.2 敏感系数 β 对内生变量的影响

价格敏感系数与乘客出行所受价格影响作用相关联，假定外生变量价格敏感系数β发生改变，此时a= 8，ζ= 0.5，c1= 5，c2= 0.05，h= 10，ρ= 15，而β2在0.001至0.01的合理范围内升高至0.005时，此时乘客更倾向于选择价格更为低廉的公共交通出行手段，分析在该情况下对轨道交通运营定价p、客流量λ及政府的财政补贴额度f产生的影响。分别将外生变量β1与β2代入p，f，λ的函数表达式中，可以得到价格敏感系数β对内生变量的影响如图2所示。

当保持其他外生变量数值不变时，当价格敏感系数β的数值不断增大，可认为在一定条件下，乘客选择价格较高的地铁出行倾向性较低。在该情况下，运营定价p随之降低，由3.35元/人降低至3.3元/人；但此时客流量λ呈现上升趋势，由6 050万人次提升至6 200万人次；同时政府应当通过提高财政补贴额度至2.56元/人，以促进城市轨道交通的快速发展。

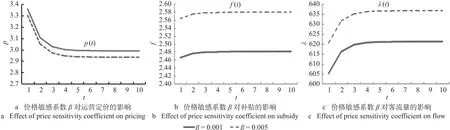
图2 价格敏感系数β对内生变量的影响Fig.2 Effect of price sensitivity coefficient on endogenous variables

2.3 价格调整因子ζ对内生变量的影响

价格调整因子的改变将对政府给予的补贴力度产生影响，假定外生变量价格调整因子ζ发生改变，此 时a= 8，β= 0.001，c1= 5，c2= 0.05，h= 10，ρ= 15，而ζ2在0至1的合理范围内由0.5升高至0.7时，分析在该情况下对轨道交通运营定价p、客流量λ以及政府的财政补贴额度f产生的影响。分别将外生变量ζ1与ζ2代入p，f，λ的函数表达式中，可以得到价格调整因子ζ对内生变量的影响如图3所示。

价格调整因子ζ是政府根据消费者可接受的销售价格与实际的销售价格之间的差价进行调节的因子，调节力度越大，价格越低。当保持其他外生变量数值不变的情况下，通过改变价格调整因子ζ，随着价格调整因子ζ数值变大，即政府给予的财政补贴力度越大，在该情况下，轨道交通运营定价p不断降低，由3.35元/人降低至3.25元/人；随之客流量λ增加，由6 050万人次上升至6 130万人次；政府的财政补贴额度f也将升高，由2.46元/人上升至2.56元/人。

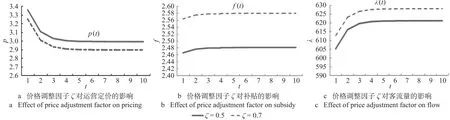
图3 价格调整因子ζ对内生变量的影响Fig.3 Effect of price adjustment factor on endogenous variables

2.4 成本系数c对内生变量的影响

成本系数与运营公司就运营方面投入的成本相互关联，假定外生变量成本系数c发生改变，此时a= 8，β= 0.001，ζ= 0.5，c1= 5，h= 10，ρ= 15，而成本系数c2由0.05上升至0.07，由于提高运营服务水平需要投入大量的成本，在该情况下运营成本受影响而增高，分析该情况对轨道运营定价p、客流量λ以及政府的财政补贴额度f产生的影响。分别将外生变量c2= 0.05与c2= 0.07代入p，f，λ的函数表达式中，可以得到成本系数c对内生变量的影响如图4所示。

当成本系数c2增大时，轨道交通运营定价p升高，由3.35元/人上升至3.45元/人；但客流量λ降低，由6 000万人次降低至5 000万人次；同时政府的财政补贴额度将减小，由2.5元/人降低至1.5元/人，可见成本系数对地铁各要素的影响较为显著。因此，政府通过采取财政补贴方式可以对维持城市轨道交通运营的整体运输效率起到一定控制效果。

图4 成本系数c对内生变量的影响Fig.4 Effect of cost coefficient on endogenous variables

2.5 研究结论

基于福州地铁1号线2018年运营现状，福州地铁车票均价约为3.5元/人，在该定价水平下，结合外生变量数值求解函数曲线显示，年乘车人次约为5 800万人次，与现实情况较为接近，同时补贴额度的求解结果约为2.45元/人。

就价格敏感系数β而言，若乘客的价格敏感系数β较高，运营方应适当调低定价，政府则相应提高补贴额度。在价格敏感系数β由0.001上升至0.005时，车票的最优定价与补贴额度分别为3.3元/人与2.55元/人。就价格调整因子ζ而言，政府加大对地铁运营补贴的投入力度，提高价格调整因子ζ水平，将对降低定价、提高客流量具有显著影响。在价格调整因子ζ由0.5上升至0.7时，政府的财政补贴约为3.1元/人，车票的最优定价与客流量分别为3.35元/人与6 100万人次。就成本系数c而言，为提高运营服务水平，成本系数c难免将增大，随之产生地铁票价升高、客流量降低、补贴额度减小的情况。因此，运营商应通过创新手段提高服务水平，同时应尽可能避免运营成本随之增加。若无法阻止运营成本上升，政府应及时根据实际情况提高财政补贴额度以确保福州地铁的可持续发展。

3 结束语

随着城市轨道交通建设进程的加快，建立并完善适应市场的定价机制将成为提升轨道交通竞争力和运营效益的有力途径。通过构建Stackelberg微分博弈模型，分析内生、外生变量对博弈模型产生的影响，并结合福州地铁1号线运营情况展开分析，旨在为我国城市轨道交通快速建设、稳定发展提供一定的决策支持。此外，在城市轨道交通运营的补贴与定价问题研究过程中，参数选取方面还存在不足。为提高城市轨道交通运营公司与政府在解决补贴与定价问题中的博弈可信度，后续研究将围绕增设相关参数、增加项目案例支撑等手段展开，从而不断推进博弈论在解决城市轨道交通运营问题中的应用，提高经济效益和社会效益。