一种使用分区逻辑合并的IMA分区分配方法
2019-07-12郑磊
文/郑磊
1 引言
分区向模块的分配问题是IMA航电总体配置必须要涉及的问题,在分配过程中需要综合考虑模块调度和通信延迟等限制条件。若将分区看作是周期运行的任务,那么分区向模块的分配就类似于多处理器任务分配问题。O.Kermia[2]与J.Korst[3]等人针对无占先限制的周期任务向多处理器分配的问题提出了快速启发式算法;T.Davidovic[4]等人针对在多处理器上非周期任务调度问题引入了MILP公式;S.Thanikesavan[5][6][7]探讨了基于MILP公式的的多处理器周期任务调度问题。针对IMA分区分配问题,P.Bieber[8][9]等人从安全性和可靠性需求角度研究了应用向模块分配的问题;Ahmad[10]等人针对这一问题,通过将所有的约束条件线性化利用了MILP方法,在使用图论进行一步初始化简化变量数量后对该方程进行解析求解。由于问题本身变量数量的庞大,问题解算时间随着分区数量和模块数量的增多而增加,因此必须采用必要的简化方法减少分区分配问题的解算时间,使用图形理论进行问题简化是非常有效的方法。
本文使用图形理论对分区分配问题进行进一步简化,提出分区合并算法达到减少算法解算时间的目的。
2 分区分配模型
以M表示Nm个IMA模块的集合,即M={m1,m2,…,mNm,},P为Np个分区的集合,即M={p1,p2,…,pNp,}。设各个IMA模块具有同一性,即任意分区pj∈P可以在任意模块mk∈M上运行,分区的执行时间并不依赖于任一模块。任意模块mk∈M具有两个基本属性,分别为总可用存储空间Rk和最大分区数Nk。由于模块的同一性,设模块间的通信延迟为一定值,则分区间的通信延迟主要由分区通信本身决定。分区间的通信延迟受模块影响部分可用一延迟矩阵Δ来表示:

其中δi,j代表代表分区pi和pj分配到不同模块后的通信延迟受模块影响部分。
任一分区pj∈P具有如下属性:
(1)ΕjP,分区pj的执行时间;
(2)TjP,分区pj的运行周期,显然有ΕjP≤ TjP;
(3)rj,分区需求的存储空间。
以tj(1)表示分区pj的第一次执行的开始时刻,那么由于分区运行的严格的周期性,它的第k次运行的开始时刻tj(k)则为:
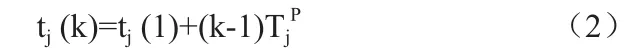
出于某些安全性考虑,可能出现某两个分区不可以分配到一个模块中的情况。以 表示这样的分区组(pi,pj)∈P2的集合,其中分区pi和pj不可以分配到同一模块。
系统中的各个分区在运行时会进行各种形式的通信,在行为上表现为接收和发送数据。以Λ表示系统中所有NΛ个通信路径向量的集合,即其中λir表示第i个通信路径向量,它由该路径所经过的所有r个分区序列组成,若通信路径λir先后经过分区 pj,pk…pl,有 λir=(j,k,…,l)。 以 L(λir)表示 通信路径λir端到端的通信延迟。
定义一个包含二进制变量ai,j的矩阵A来表示分区向模块的分配。

在分区向模块分配过程中一个正确的分区分配必须满足如下三种限制条件:
(1)调度限制:分配到同一个模块中的分区不能有执行时间上的重叠。
(2)资源限制:分配到同一个模块的所有分区所需求的存储空间之和要小于模块的总可用存储空间;分区数量之和要小于模块可载有的最大分区数;一个分区只能被分配到一个模块中;满足(pi,pj)∈ε的两个分区不能分配到同一模块中。
(3)通信延迟限制:每一个通信路径端到端的延迟L(λir)要小于最大可允许的延迟上限 Lmax(λir)。在给定分区集合向多模块分配的问题中,就是要寻找一个方法使得该方法产生的结果能够满足上述所有的限制条件。
2.1 分区分配中的调度限制
由式(2)可得分区pj第k次运行的时间区间为Ik(tj(1) )=[tj(k),tj(k)+ΕjP]。限制条件:分配到同一个模块中的任意两个分区pi和pj不能有执行时间上的重叠就可以表述为
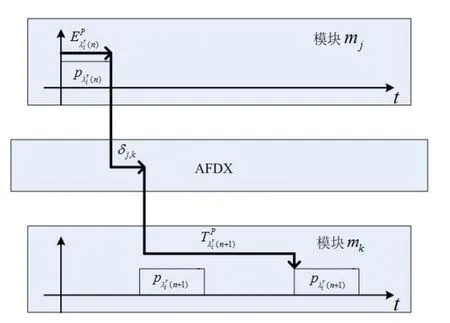
图1:模块间通信延迟
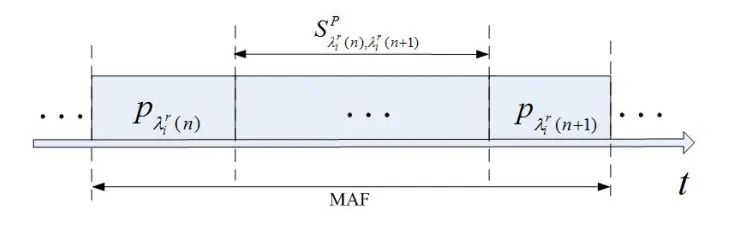
图2:同一模块内分区的调度延迟

Korst在文献[3]中提出的两个周期任务执行时间不发生重叠的充分必要条件可以应用于分区调度范畴中:

其中,gi,j为分区周期TiP与TjP的最大公约数。
分区对处理器的总占用率Uim不能大于1,若模块mi分区数为ni,有:
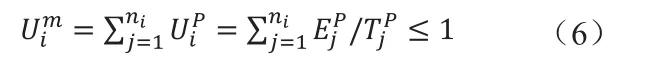
其中UiP=ΕjP/TjP为分区pj的处理器占用率。
2.2 分区分配中的资源限制
分配到同一个模块的所有分区所需求的存储空间之和Rjm要小于模块的总可用存储空间可表示为:
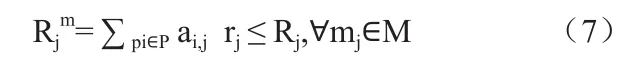
分配到同一模块上的分区数量之和要小于模块可载有的最大分区数可表示为:

一个分区只能被分配到一个模块中可表示为:

满足(pi,pj)∈ε的两个分区不能分配到同一模块中可表示为:

2.3 分区分配中的通信延迟限制
在分区分配过程中,对任意通信路径λir∈Λ,端到端的延迟 L(λir)要小于最大可允许的延迟上限。端到端的通信延迟为整条通信链路中的分区的执行时间与分区间通信延迟之和,可用下式表示:
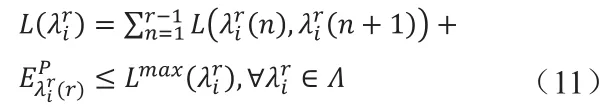
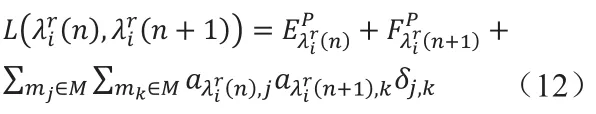
3 使用分区逻辑合并简化模型
由式(5)可获得在分区调度限制下不可分配在同一模块上的分区组的集合,并使之与满足 (pi,pj)∈ε的集合合并为集合 Ε,(pi,pj)∈Ε则为所有不可分配在同一模块上的分区组的集合。
由式(11)和(12)可得任意通信路径延迟的最大值为:


其中 L'(λir)和 Lmax'(λir)分别为只考虑分区分配造成的最大延迟和该延迟的上限值。若 L'(λir)>Lmax'(λir),则该通信路径中至少有两个分区必须分配到同一模块上,对于通信路径最多可以有r-1个这样的分区组合。
采用图型理论进行模型简化可以在极大限度上减少变量的数量。在分区分配问题中可采用如图3所示分区关系图G[10]:
在图3中,每一个节点代表一个分区,两个分区间的连线表明这两个分区可以分配到同一个模块上,反之没有连线的两个分区则不能分配到同一模块上,即满足(pi,pj)∈Ε。
类似于最大无关组(MIS)[11]的概念,在该图中可以找到这样一个集合B,该集合包含的所有分区彼此互相不能分配到同一模块上,如在该图中有(p1,p3,p6)∈B。在分区路径λir延迟 L'(λir)>Lmax'(λir)的约束下,可以找到r-1个必须分配到同一模块的分区组合,并将pi,pj两个分区合并成一个节点pi,j进行考虑,在合并的同时,新节点要继承原先节点与其他节点互斥关系。设集合Dg为以pi,j为元素的集合,即pi,j∈Dg。在图3中,虚线表示一条通信路径λ14,它先后经过分区p1,p5,p6,p7,若有Lmax'则(p5,p6)或(p6,p7)必须分配在一个模块中,将(p5,p6)节点合并后的关系图Gg'为图4,(p6,p7)的合并与之同理。
4 分区分配方法流程
整个分区分配算法包含如下几步:
(1)由式(5)解算出所有满足(pi,pj)∈Ε的分区组合,并作出分区间关系图G。
(2)由式(15)和(16)对每一条通信路径进行分析,求解出所有pi,j∈Dg,并在关系图G中合并相关的pi和pj获得关系图Gg'。若总共有Nλ条通信路径,则关系图Gg'的最大数量NG为
(4)将Bg所包含的分区分配到每一个模块中(一个模块最多分配一个分区或合并后的分区对)。设必须分配到模块mk中的分区组成的集合为若有pi∈Bg必分配到模块mk中,则有
(6)对所有Nm个模块作运算其 中 l=1,2,…,Nm,且l≠k获得只能分配到模块mk的分区,并将同时满足式(6~8)条件的分区分配到模块mk。
(7)重复5)和6),直到无法获得只能分配到一个模块中的分区。这样就可以获得对应于每个Gg'的两种数据:其一为必须分配到各个模块的分区集合其二为可分配到两个以上模块的分区集合和每个分区 pi∈Pg'可以分配的模块的集合Mpig。集合Pg'所含分区只须满足式(6~8)的限制条件就可以分配到各个模块。
(8)在集合Mpig中,找出当前模块处理器占用率最小的模块mk,将集合Pg'中处理器占用率UjP最大的模块分配到mk中,分配的同时要满足式(7)和(8)的约束条件。
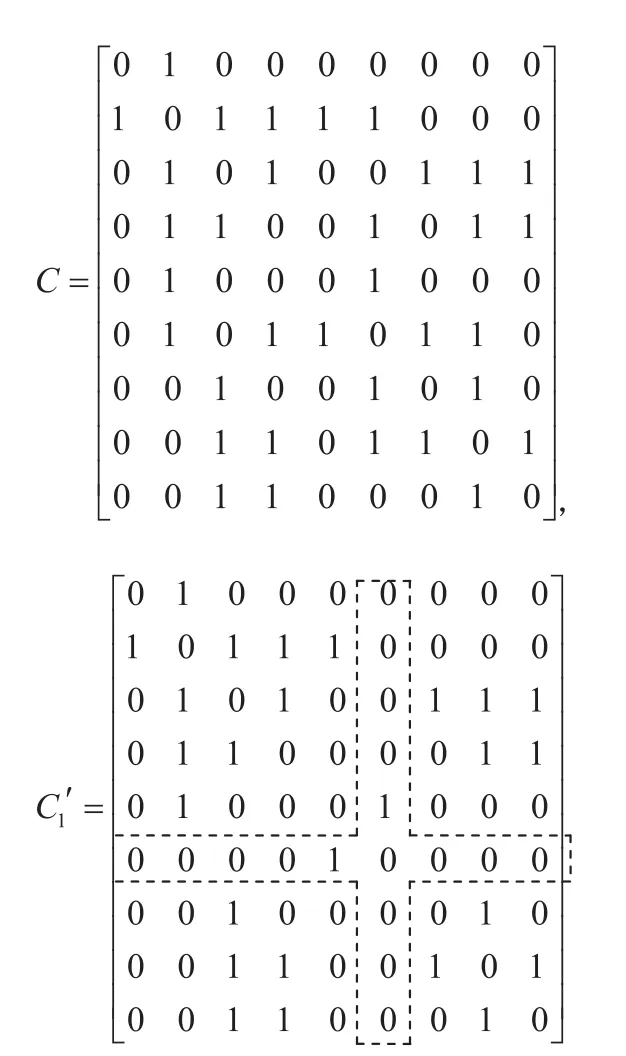
引入Np维矩阵C=[ci,j]表示分区之间的关系,若分区pi,pj可以分配到同一模块上,则ci,j=1,反之 ci,j=0,ci,j=cj,i,若 i=j规定 ci,j=0。分区间的合并可以通过矩阵元素间的逻辑运算来表示,算法如下:若分区pj和pk(j 若分区关系如图3,分区合并情况如图4则有 该算法的流程如图5。 由此,即可获得对应于每个Gg'的和。 从算法解算过程可以看出,整个解算过程所需的逻辑运算次数较少,通过引入矩阵元素间的逻辑运算,使算法便于编程实现,并通过引入分区合并机制减少了运算次数,是一个可行的分区分配问题解决方案。 图3:分区关系图 图4:合并后的分区关系图 图5:分区分配算法流程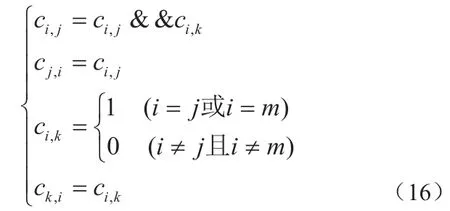
5 结语